Моделирование морфологии эритроцита и расчет внутриклеточного давления по данным атомно-силовой микроскопии

Метод атомно-силовой микроскопии находит все более широкое применение в биологии и медицине. Атомно-силовая микроскопия имеет ряд преимуществ перед оптическим или электронным микроскопами. Помимо трехмерной визуализации, атомно-силовая микроскопия имеет возможность анализа механических свойств, что позволяет более глубоко изучать клеточные процессы, выяснять такие важнейшие свойства, как эластичность, мобильность поверхностных слоев, адгезия, молекулярное связывание и электростатичность.

В настоящее время формируется новое направление в цитологии, которое определяют термином «клеточная наномеханика», или «клеточная эластография». Эти понятия подразумевают методы визуализации сдвиговых упругих характеристик биологических мягких тканей, которые дополняют традиционные способы визуализации и считаются перспективными для медицинской диагностики различных патологий, особенно при изучении онкологических заболеваний [1, 6, 7, 10, 13–15, 20].

Работы по изучению биологических объектов с помощью методов атомносиловой микроскопии активно ведутся в отношении красных клеток крови – эритроцитов. Изменение формы эритроцитов может возникать вследствие внешних физико-химических воздействий, т.е. клетки могут подвергаться различным обратимым и необратимым трансформациям. Состояние мембраны эритроцитов и работы ионных насосов мембраны однозначно меняет внутриклеточное осмотическое давление, что, в свою очередь, изменяет морфологию эритроцита и его объем.

Взаимосвязь между состоянием мембраны эритроцита и его внутриклеточным давлением и морфологией можно описать следующим образом. Исходя из термодинамического принципа минимизации свободной энергии липидного бислоя мембраны в работах [13, 20] трехмерная форма эритроцита рассчитывается аналитически. На основании этого и модели регуляции ионного обмена и, соответственно, объема эритроцитов в работах [7, 14, 15] приводятся численный расчет взаимосвязи внутриклеточного давления и объема эритроцита, в том числе с учетом биомеханической модели оболочки [1, 15]. Данные модели согласуются с экспериментальными данными, подтверждающими изменение объема эритроцита при изменении ионного обмена под действием различных внешних химических факторов, изменяющих pH раствора.

Однако для сравнения расчетных данных с экспериментальными данными, полученными методами атомно-силовой микроскопии, указанные модели необходимо дополнить по нескольким причинам [1, 4–6, 8, 9, 11, 12, 16–19]. Во-первых, измерение методами атомно-силовой микроскопии наиболее часто проводится в воздушной среде, в которой эритроцит теряет до 70 % массы из-за потери воды. В результате форма эритроцита не меняется, а его объем на 95–99 % заполнен гемоглобином [1, 10], в то время как в работах [7, 14, 15] предполагалось, что содержание гемоглобина находится в диапазоне 50–80 %. Во-вторых, соотношение объем–давление в термодинамической системе, в которой происходит существенное влияние гемоглобина на мембрану эритроцита, будет меняться, что кратко упоминается в работах [1, 7]. Так, в работе [7] был изучен процесс расширения эритроцита под действием внутреннего давления, которое менялось в широком диапазоне – от единиц паскалей до 5 кПа. Расширение до 40–60 % по отношению к начальному объему происходило под действием небольшого давления до 2 Пa за счет изменения формы, затем модель эритроцита приобретала форму шара и расширение происходило за счет растяжения мембраны, что требует на три порядка больше давления. При этом моделирование уменьшения объема из-за обезвоживания или под действием сил сжатия выполнено не было. И, наконец, при экспериментальном исследовании методами атомно-силовой микроскопии происходит осаждение эритроцитов на поверхность, их адгезия и изменение формы под действием сил адгезии и тяжести [4, 5, 11, 12, 17, 18]. Таким образом, целью настоящей работы является численный расчет морфологии эритроцита в зависимости от внутриклеточного давления для анализа данных атомно-силовой микроскопии, т.е. для случая, когда эритроцит находится в воздушной среде на предметном стекле.

Модель эритроцита и численный расчет морфологии

Существует ряд моделей, которые описывают процессы регуляции ионного обмена и объема эритроцитов [1, 6, 7, 10, 13–15, 20]. Основное внимание в этих работах уделено биохимическим и электрохимическим процессам, влияющим на регулирование объема. Показано, что система ионных насосов и каналов в мембране клетки (Na+, К+-насос, Ca+ -активируемые К+-каналы) обеспечивает заданный объем клетки и его стабилизацию. Перенос ионов осуществляется при помощи ферментов класса гидролаз аденозинтрифосфатазы, катализирующих отщепление от аденозинтрифосфорной кислоты одного или двух остатков фосфорной кислоты. В процессе биохимической реакции происходит освобождение энергии, используемой при транспорте веществ через мембрану. Высокое соотношение концентрации калия во вне- и внутриклеточной жидкости (38:1) поддерживается благодаря действию Nа+, К+-аденозинтрифосфатазы, активно переносящей ионы калия в клетку, а ионы натрия из нее в соотношении 2:3 [6]. Вследствие активного выведения натрия из клеток Na+, K+-аденозинтрифосфатазы 85–90 % всего натрия, содержащегося в организме, находится во внеклеточной жидкости. Аденозинтрифосфатаза белков плазматических мембран осуществляет аденозинтрифосфатазозависимый трансмембранный перенос Na+ и К+-ионов в клетках, что обеспечивает поддержание электрохимического и осмотического градиентов одновалентных ионов, необходимых для нормального функционирования клеток.

В результате работы ионных каналов в клетке возникает асимметрия в распределении концентраций ионов внутри и вне клетки, что обеспечивает поддержание ее постоянного объема. Создаваемое обменными процессами осмотическое давление в клетке эритроцита вызывает деформацию оболочки. При этом морфология эритроцита задается липидным бислоем, что определяется внутренними силами, возникающими вследствие построения белков слоя (фосфолипидов) неполярными концами внутрь слоя. Возникающая из-за ионного взаимодействия механическая энергия липидного бислоя стремится принять минимальное значение и формирует морфологию эритроцита [1, 2, 9].

Для расчета влияния ионных насосов на регуляцию объема эритроцита составляют систему уравнений [1, 6, 7, 10, 14, 15], которая включает потоки ионов и поток воды. При этом известно [1], что основной вклад в регуляцию объема эритроцитов человека вносят катионы калия и натрия, а также анионы хлора и HCО 3 . Кинетика внутриклеточных концентраций калия и натрия описывается уравнениями, которые учитывают активный транспорт этих катионов Na⁺, K⁺-аденозинтрифосфатазы и пассивный поток через мембрану по градиенту концентрации. Учитывая условие электронейтральности внутриклеточного содержимого эритроцита, получают известное уравнение зависимости изменения объема от осмотического давления в эритроците:

d ( V 1 dt I V 0 J

SP        SP

= J = —LЯ ₀A C =    9_H0 ,

H2O V H2O        V    H2O RT где V и V0 – текущее и физиологически нормальное значение объема эритроцита, а поток воды JH2O пропорционален разности концентраций ∆С осмотически активных ионов внутри и снаружи мембраны эритроцита, которая выражается через осмотическое давление ∆P и тепловой потенциал RT; S – площадь мембраны, ϑH2O – молярный объем воды и Pf – осмотическая проницаемость мембраны для воды.

В работах [3, 7] был выполнен численный расчет уравнения (1) с учетом упругого воздействия оболочки на обменные процессы и изменения объема эритроцита. Благодаря способности сопротивляться деформированию оболочка эритроцита оказывает воздействие на процесс осмоса в виде реактивного давления Δ P r , которое приложено к объему, заключенному в эритроците. При этом в расчетах по формуле (1) вместо давления Δ P ставилась разность Δ P– Δ P r . Модель показала хорошее соответствие с экспериментальными данными об увеличении объема эритроцита в процессе образования ионных каналов в мембране после обработки эритроцитов амфотерицином В и вызванного этим увеличения проницаемости для ионов, а также об увеличении объема по причине уменьшения осмотичности среды [7].

В случае проведения измерений при помощи атомно-силового микроскопа наиболее часто параметры эритроцита определяются с использованием мазка крови на стекле, где эритроциты расположены тонким слоем и находятся в воздушной среде. Как было показано в работах [1, 4, 5, 8, 9, 11, 16–18], на воздухе происходит выход воды из эритроцита и, соответственно, уменьшение его объема в 4–6 раз. Поскольку при измерениях с помощью атомно-силовой микроскопии в процессе высушивания образца с эритроцитами водная среда исчезает, возникает большой градиент Δ P , в соответствии с формулой (1) происходит выход воды из эритроцита и потеря его массы и объема. При этом форма эритроцита остается неизменной и определяется состоянием его мембраны [1, 4, 5, 8, 9, 11, 16–18], т.е. реактивным давлением Δ P r .

С одной стороны, реактивное давление мембраны эритроцита Δ P r будет зависеть от состояния мембраны, с другой стороны, морфология эритроцита будет зависеть от биомеханики его мембраны [8, 9, 13, 16, 18, 20]. Таким образом, для определения внутриклеточного давления по данным атомно-силовой микроскопии необходимо провести численный расчет, в котором задается начальное реактивное давление Δ P r , и получить зависимости морфологии эритроцита от его величины.

За основу модели для численного расчета были взяты известные справочные данные и биомеханическая модель однородного тела, покрытого мембраной, состоящей из липидного бислоя, упругие свойства которого описаны в работах [13, 20] и задаются несимметричным тензором, что формирует морфологию эритроцита. Для решения системы уравнений использовался программный продукт PARDISO ( Parallel Direct Solver ), библиотечная подпрограмма которого применялась для решения системы линейных уравнений с невырожденной разреженной матрицей методами суперузлового исключения Гаусса, а также разложениями Холецкого. Для проведения численного расчета методом конечных элементов применялся программный комплекс Comsol multiphysics (лицензия 1029477) и модуль оптимизации пакета прикладных программ MATLAB (лицензия 512916) [8, 9, 16, 18].

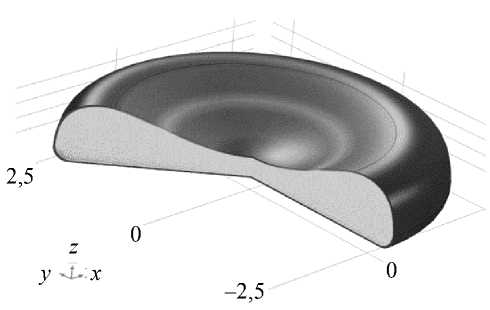
Для численного моделирования рассматривалась связная задача взаимодействия твердого тела (мембрана клетки) и жидкости (внутреннее содержимое эритроцита). В работе решалась параметрическая задача, в качестве параметра использовалось значение реактивного давления ΔPr, создаваемого мембраной эритроцита, геометрия эритроцита представлена на рис. 1, а. В расчетах принимались следующие обозначения осей координат: r – горизонтальная, z – вертикальная, φ – угловая. В численном эксперименте рассматривается осесимметричная задача, ось тела вращения проходит через центр эритроцита (r = 0). В расчетах модель линейного эластичного материала основывалась на следующих уравнениях:

-Va = Fv , a = 5 ,(2)

5 - 5о = C : (E — Eо — Eine, ) ,(3)

e = 2[(VuSoM )T +VusoUd ] ,(4)

где a - тензор напряжений, a = 5 ; F_V - сила, действующая на тело; £ - тензор деформаций; e _inel - тензор тепловой деформации; 5 ₀, E ₀- начальные значения соответствующих тензоров; С – тензор упругости четвертого порядка; “:” – операция тензорного произведения; u_solid – вектор компоненты смещения, для расчетов мембраны применяется модель эластичного материала.

а

1,5

0,5

r , мкм

б

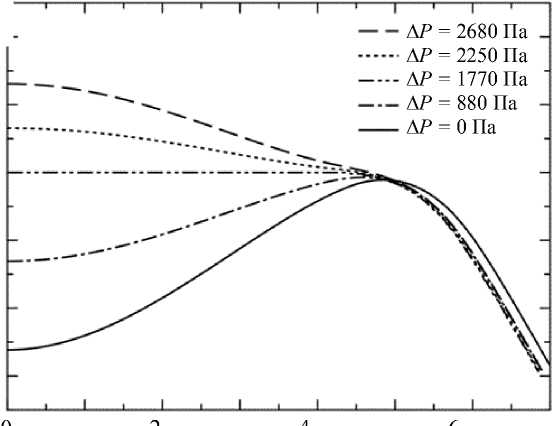
Рис. 1. Результаты расчета морфологии модели эритроцита под действием давления: а – трехмерная модель эритроцита, на которой показан боковой срез; б – зависимость формы среза эритроцита от разности давлений на мембрану эритроцита, отрицательные значения – давление внутри превышает давление снаружи

При этом начальные смещения равны 0, на внешней границе твердого тела задаются начальные и граничные условия следующего вида:

О ■ n = F a ,

F a =

f 0 ) (a P r J

где n – нормаль к поверхности; FA – вектор внешнего воздействия; ΔPr – реактивное давление, задаваемое в расчетах как параметр. Данное условие обеспечивает направление вектора давления вдоль вертикальной оси. На оси вращения установлено условие симметрии. Нижняя граница эритроцита зафиксирована от смещений вдоль оси z:

w soid = ⁰ . ⁽⁶⁾

Физические свойства твердого тела задаются в соответствии с известными экспериментальными данными [1, 3, 9, 19]: модуль упругости оболочки равен 1200– 2000 Па в зависимости от координаты r [5, 8, 9, 16–18], плотность оболочки – 1200 кг/м³ [3, 13, 10, 20], коэффициент Пуассона оболочки – 0,33 [5, 7, 9]. Тензор деформации обусловлен упругими свойствами мембраны: жесткостью на сдвиг, равной 0,006 мН/м, и на растяжение, равной 450 мН/м [1, 7]. При этом математическая модель гидродинамики описывает поведение внутреннего содержимого модели эритроцита, существенное отличие от модели мембраны состоит в том, что жидкое содержимое может двигаться и изменять свое местоположение в зависимости от приложенного давления со стороны мембраны. В результате во внутренней области эритроцита проводится моделирование жидкой среды с использованием уравнений Навье–Стокса и неразрывности:

p (m „            , = V • py fluid ) fluid

- PI + ^ ( ^V u fluid

T 2

+ (Vuflud ) )- 3 ^(V

■ u fluid ) I + F ,

V^(p u fluid )= 0 ,

где ρ – плотность жидкости; u fluid – вектор скорости; p – давление жидкости; I – единичный тензор; µ –динамическая вязкость; F – вектор внешних воздействий.

При расчетах считалось, что в начальный момент времени скорость и давление в жидкости равны 0. Условие на границе твердой и жидкой сред позволило отслеживать влияние деформации на объем сжатой жидкости и давление внутри эритроцита и соответствует следующим уравнениям:

,

flu idw

8 u,„.,„, solid u,

w

G^ n = Г - n , Г =

-PI + Ц ( Vu fluid + ( Vu fluid ) T ) - 3 Ц ( V ■ u fluid ) I где uw – скорость деформации твердого тела; Г – сила, действующая на границу жидкости и твердого тела.

При этом физические свойства жидкости определяются следующими значениями: плотность жидкости – 1000 кг/м3, динамическая вязкость – 4 мПа∙с [3, 13, 18–20]. В процессе расчетов использовалось конечно-элементное разбиение, в котором сетка содержала порядка 13 700 треугольных элементов, при этом размер конечноэлементной ячейки уменьшался при приближении к границе между жидкостью и твердым телом.

Таким образом, расчет внутриклеточного давления проводился без использования подгоночных параметров в два этапа. Сначала внутреннее содержимое эритроцита представлялось в виде жидкости или подвижного (сыпучего) материала, задавалось давление, осуществлялся расчет и формировалась геометрия под действием внутренних и внешних сил, при этом расчет проводился с использованием уравнений Навье–Стокса. Интересно, что при этом разница давлений на мембрану составляла не более 2 Па, что соответствует данным работ [1, 7]. Затем расчет проводился повторно методом конечных элементов, при этом внутреннее содержимое эритроцита предполагалось твердым, что исключало движение внутри эритроцита, но позволяло определить внутриклеточное давление, которое устанавливается в равновесии. Естественно, установившееся давление внутри клетки отличалось от начального и принимало значения порядка единиц или десятых килопаскаля, что соответствует данным атомно-силовой микроскопии при измерении модуля Юнга.

На рис. 1, б представлена зависимость формы среза эритроцита от разности давлений на мембрану эритроцита, которая устанавливается после завершения расчета. Видно, что с ростом внешнего давления происходит небольшое расширение модели эритроцита и существенный прогиб в центре мембраны, что соответствует экспериментальным расчетам геометрии среза эритроцита по данным атомно-силовой микроскопии. Необходимо отметить, что при пропорциональном увеличении или уменьшении размеров модели эритроцита установившиеся значения давления внутри клетки не изменялись. Данный факт соответствует теории ионных каналов, поскольку в формуле (1) используется только отношение V/V 0 .

Экспериментальные результаты

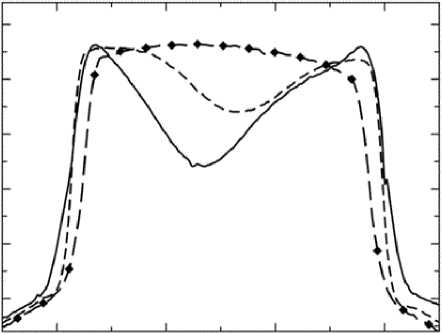
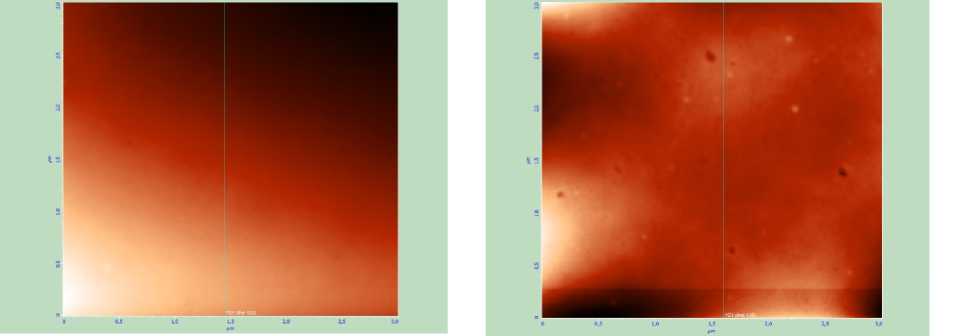
Для расчета внутриклеточного давления в работе проведены экспериментальные исследования методом атомно-силовой микроскопии в полуконтактном режиме на микроскопе Solver – P 4 компании NT – MDT , при этом в качестве образцов использовались мазки крови, взятые у экспериментальных животных (мини-пигов – миниатюрных свинок) с различной степенью заболевания механической желтухой (классы А , B и C ) и у здоровых особей (в норме). Результаты исследований приведены на рис. 2 и 3, при этом показаны только вертикальные срезы эритроцитов (рис. 2, а ), которые позволили определить степень изменения глубины впадины мембраны эритроцита в центре и его объем. Полученные усредненные данные измерений по всем эритроцитам на скане приведены в таблице. Механическая желтуха характеризуется тем, что при повышении класса заболевания в крови растет концентрация билирубина, который разрушает мембрану эритроцитов, проникает внутрь, распространяется по организму и приводит к накоплению в печени и других органах [2]. На сканах эритроцитов, полученных с помощью атомно-силовой микроскопии, видно (см. рис. 3), что с ростом степени заболевания происходит рост как количества, так и размеров нарушений в мембране. Кроме этого, оказалось, что в норме эритроцит имеет форму двояковогнутого сфероцита, при нарастании гипербилирубинемии или концентрации билирубина в крови эритроцит меняет форму: из сфероцита превращается в овал, из двояковогнутого становится двояковыпуклым. Все эти данные свидетельствуют о разрушении мембраны эритроцитов и нарушении ее функции, что, вероятно, приводит к изменению ее биомеханических свойств.

По трехмерным данным скана мазка крови был выделен каждый эритроцит в отдельный блок данных, по которым проведен расчет геометрических характеристик разрезов эритроцитов, а также рассчитан объем. Усредненные значения объема эритроцитов и глубины впадины в центре приведены в таблице, в которой также представлено расчетное значение внутриклеточного давления для среднего значения отношения V/V0.

Видно, что с увеличением степени механической желтухи происходит рост среднего по скану объема эритроцита, соответствующее изменение деформации мембраны в центре эритроцита и увеличение его внутриклеточного давления.

нм

мкм

а

2         4         6          8

Класс С Класс А

Норма x, мкм б

Рис. 2. Морфология эритроцита, полученная при помощи атомносиловой микроскопии: а – трехмерное изображение эритроцита; б – поперечный срез трехмерного изображения для эритроцитов при разной степени механической желтухи и в норме

Размеры эритроцита при разной степени механической желтухи и результаты оценки отношения внутриклеточного давления к показателю в норме

Степень механической желтухи	Объем эритроцитов, мкм3	Отношение объема к объему в норме, %	Внутриклеточное давление, кПа
Норма	7,5 ± 2,0	100,0 ± 26,7	0
Класс А	8,8 ± 1,3	117,3 ± 17,4	1,6
Класс В	10,2 ± 1,9	136,0 ± 25,2	3,4
Класс С	12,3 ± 2,2	164,0 ± 29,3	6,3

Норма                                   Класс А

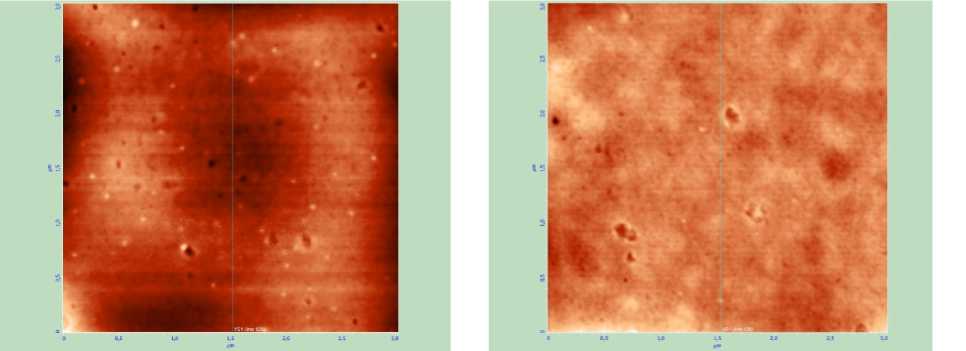
Класс B

Класс C

Рис. 3. Сканы поверхности мембраны эритроцита, полученные при помощи атомно-силовой микроскопии с размером изображения 3×3 мкм, для эритроцитов с различным уровнем механической желтухи и в норме

Заключение

Таким образом, в работе предложен способ оценки внутриклеточного давления эритроцитов на основе численного моделирования морфологии эритроцита и данных атомно-силовой микроскопии. Проведен расчет внутриклеточного давления эритроцитов для экспериментальных животных при механической желтухе разной степени. Показано, что с ростом концентрации билирубина в крови происходит нарушение мембраны эритроцитов, в среднем увеличение их объема и существенное изменение внутриклеточного давления. Величина внутриклеточного давления в перспективе может быть использована для диагностики состояния мембраны эритроцитов.

Благодарности

Работа выполнена при поддержке Федеральной целевой программы «Исследования и разработки по приоритетным направлениям развития научнотехнологического комплекса России на 2014–2020 годы» (соглашение № 14.574.21.0025, уникальный идентификатор соглашения – RFMEFI 57414 X 0025).