Моделирование неопределенности при помощи нейронных сетей

Развитие предприятий авиационной промышленности основывается на разработке и внедрении в производство инновационных компонент авиационной техники. Это требует принятия управленческих решений, которые, в свою очередь, характеризуются некоторым уровнем неопределенности. Острой проблемой, с которой сталкиваются предприятия, является анализ неопределенности и эффективное управление ею.

Проблема количественной оценки является сложной и комплексной задачей, в настоящее время недостаточно освещенной в научной литературе. Понятие неопределенности встречается в разных областях науки, но существующие подходы к оценке неопределенности основаны на оценке параметров и закладывают в это понятие некоторую погрешность.

В рамках исследования авторы рассматривают методы количественной оценки уровня неопределенности и разрабатывают нейросетевую модель неопределенности при принятии управленческих решений.

МЕТОДОЛОГИЯ (ТЕОРЕТИЧЕСКИЕ ОСНОВЫ) ИССЛЕДОВАНИЯ

Современные исследователи трактуют понятие «неопределенность» следующим образом. Ученые К. Фрей, Д. Пенман и Л. Ханле и др., занимающиеся исследованием парниковых газов, рассматривают «неопределенность» как «недостаток знания истинного значения переменной, которая может быть описана как плотность распределения вероятности (ПРВ), характеризующий диапазон и вероятность возможных значений». По их мнению, неопределенность напрямую зависит от уровня компетентности аналитика, что, в свою очередь, «зависит от качества и количества применимых данных, так же как и от знания основных процессов и методов вывода» (Фрей и др., 2006, с. 3.8). Американский экономист Ф. Найт исследовал понятия риска и неопределенности и пришел к выводу, что неопределенностью следует называть непредсказуемый риск (Найт, 2003, с. 78).

Авторы настоящего исследования под неопределенностью понимают неоднозначность исхода или решения экономической ситуации. Данное определение является наиболее общим и позволяет предложить методику оценки уровня неопределенности на основе нейросетевого моделирования.

Согласно исследованиям ученых (Рымкевич, 1999; Милосердов и Герасимова, 2006; Корабейников и др., 2019; Drozdov et al., 2020, Stanton and Roelich, 2021) основными причинами неопределенности выступают:

• –    значительное количество объектов или элементов ситуации, характеризующихся большим числом параметров, которые требуют описания для управленческого решения;

• –    неточность информации и (или) ее недостаточный объем;

• –    недостаточный профессионализм лица, принимающего решения;

• –    ограничения при принятии решений;

• –    поведение и (или) реакция внешней среды на принятие решений.

Анализ неопределенности и эффективное управление ею являются острой проблемой, с которой сталкиваются предприятия.

Управление неопределенностью – это планирование, организация, мотивация, контроль формирования и реализация тактических и стратегических мероприятий по использованию фактора неопределенности в целях повышения эффективности функционирования предприятия.

Процесс анализа неопределенности необходим для исследования факторов и переменных, используемых при принятии управленческих решений, и направлен на внесение технического вклада путем количественной оценки неопределенности.

В общем случае анализ неопределенности начинается с концептуализации – набора предположений относительно структуры математической модели процесса и его методологического обеспечения. Концептуализация определяет потребность в информации, выраженной как в эмпирических данных, так и в полученных при помощи экспертной оценки (Иванилов и Лотов, 1979; Рыбников и Рыбников, 2012; Воронцовский и Дмитриев, 2014; Мадера, 2017).

Концептуализация продолжается разработкой соответствующей математической модели для оценки уровня неопределенности и сбором необходимых данных. Эти процессы тесно связаны, поскольку оказывают непосред- ственное влияние друг на друга: сбор данных обусловливает использование необходимых наборов переменных, а создание модели, в свою очередь, требует сбора определенных данных.

Далее следует процесс количественной оценки неопределенностей в соответствии с выбранной методологией и математической моделью. Последняя может быть устроена таким образом, что выявляет неопределенность сразу нескольких факторов. Поэтому для установления единого общего показателя неопределенности необходимо провести процесс сочетания неопределенностей (рис. 1).

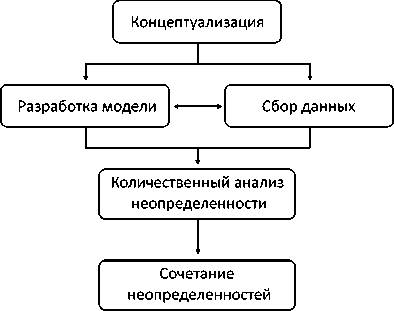
Рис. 1. Структура общего анализа неопределенности /

Fig. 1. Structure of a general uncertainty analysis

Источник: составлено авторами на основе (Куликова, 2014; Картвелиш-вили и Свиридова, 2017)

Общая неопределенность, выраженная в процентном соотношении, рассчитывается согласно уравнению:

й[А-----Ьи^, где u – неопределенность в процентах произведения величин;

^i – неопределенности в процентах, связанные с каждой i- й величиной.

Сочетание неопределенностей при сложении и вычитании величин производится по следующей формуле:

ki + - + xnl где и– неопределенность в процентах произведения величин;

^xi – значения рассчитанных величин;

Щ – неопределенности в процентах, связанные с каждой i -й величиной.

Анализ неопределенностей методом Монте-Карло заключается в выборе случайных значений исследуемых параметров, их оценке в пределах соответствующих индивидуальных плотностей распределения вероятностей и в расчете соответствующих значений. Общая схема метода Монте-Карло для сочетания неопределенностей представлена на рисунке 2.

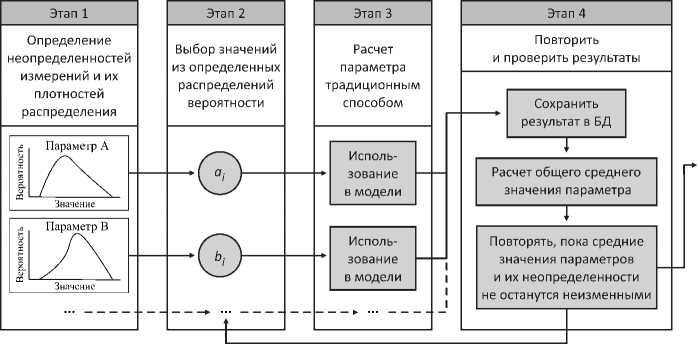
Рис. 2. Метод Монте-Карло для сочетания неопределенностей / Fig. 2. Monte Carlo method for combining uncertainties

Источник: составлено авторами на основе (Джекел, 2004; Гефан и Пальчик, 2012; Рындина, 2010).

Этап 1: определение неопределенности параметров. Устанавливаются параметры оценки, а также при помощи статистических методов соответствующие им средние величины и плотности распределения вероятностей.

Этап 2: выбор реализации случайной величины. Происходит отбор входных величин. Последние представляют собой оценки, применяемые при расчетах в разработанной модели. Это начало итерационного процесса, который сходится к средней величине параметра и его неопределенности.

Этап 3: оценка параметров. Реализации случайных величин, выбранные на этапе 2, используются для моделирования результирующего параметра.

Этап 4: повторение и проверка результатов. Результаты моделирования величины сохраняются для дальнейшего перерасчета ее среднего значения и уровня ее неопределенности; проверяются условия окончания итерационного процесса.

Можно выделить несколько подходов к моделированию неопределенности.

• 1.    Дифференциальные уравнения и стохастическое моделирование. Для моделирования принятия решений в условиях неопределенности используются различные математические теории и методы. Так, например, для составления моделей может применяться теория дифференциальных уравнений, методов оптимизации, случайных процессов и статистического моделирования. Теоретическая база данных методов обширна, применима индивидуально для каждого случая и позволяет произвести моделирование факторов неопределенности.

• 2.    Теории игр и статистических решений. Теория игр является одним из разделов современной математики, цель которого – разработка методов выбора оптимальных стратегий в различных областях деятельности. В рамках данной теории неопределенность порождается антагонистическими интересами игроков, которые играют друг против друга. Ситуация моделируется набором стратегий P и C двух игроков и платежной матрицей R .

Теория статистических решений предполагает, что неопределенность порождается возможными состояниями внешней экономической среды, для выявления которых существует градация информационных ситуаций. Определение и классификация этих информационных ситуаций составляют фундамент теории принятия решений в условиях неопределенности (Рюмкин, 2012; Kochenderfer, 2015; Шабля и др., 2018; Kureychik and Safronenkova, 2018).

Любой из перечисленных подходов предполагает определение информационной ситуации. Информационная ситуация (ИС) – это степень градации неопределенности выбора внешней средой своих состояний из заданного множества, которой располагает орган управления в момент принятия решения. Данная градация представлена в таблице.

Таблица / Table

Градация информационных ситуаций / Gradation of information situations

Информационная ситуация	Характеристики информационной ситуации
ИС1	Характеризуется заданным распределением априорных вероятностей возможных состояний экономической среды
ИС2	Характеризуется заданным распределением вероятностей с неизвестными параметрами
ИС3	Характеризуется системами линейных отношений порядков, заданными на компонентах априорного распределения экономической среды
ИС4	Характеризуется неизвестным распределением вероятностей на элементах множества возможных состояний экономической среды
ИС5	Характеризуется антагонистическими интересами среды в процессе принятия решений
ИС6	Характеризуется «промежуточными» между ИС1 и ИС5 случаями выбора экономической средой своих возможных состояний
ИС7	Характеризуется нечетким множеством состояний экономической среды

Источник: составлено авторами на основе (Ремесник, 2020).

В рамках каждой ИС определяются чистые стратегии игрока, внешней среды и составляется платежная функция. Для составления чистых стратегий внешней среды необходимо найти распределение вероятностей ее состояний. С этой целью применяется принцип максимальной неопределенности Гиббса – Джейнса, согласно которому в качестве количественной меры неопределен- ности поведения внешней среды возможно использовать натуральную энтропию Шеннона.

Значение энтропии Шеннона демонстрирует, как сильно отклонилась моделируемая система от упорядоченного состояния и насколько приблизилась к хаотичному. Малое значение энтропии говорит о структурированном, упорядоченном состоянии системы, а большое, напротив, показывает, насколько она дезорганизована и хаотична. Это характеризует полноту информации, которой обладает игрок.

Значение энтропии Шеннона вычисляется по формуле:

n

H = ~^P^ lo92Pi, где н – информационная двоичная энтропия;

n – число состояний внешней среды;

Pi – вероятность того, что система находится в i -м состоянии.

Для оценки вероятностей состояний внешней среды Qi , о которых у игрока нет никаких сведений, используются последовательности Фишберна – арифметические или геометрические прогрессии, подчиняющиеся условиям нор-мировки ^41 = 1 и неотрицательности Qi > 0, Vi.

Первая формула Фишберна (для арифметической прогрессии) имеет вид:

2(n — i + 1)

Pi ⁼--- 7----7л—< I ⁼ l--ⁿ.

n(n + 1)

Вторая формула Фишберна (для геометрической прогрессии) имеет вид:

2n~l

Qi =  -- 7^ = ^L-ⁿ .

.

Данные формулы позволяют вычислить точечные оценки состояний внешней среды и использовать их для определения энтропии Шеннона (Ремес-ник, 2020, с. 52).

Перед принятием любого решения руководители предприятий проводят оценку рисков и последствий своих решений. Любое решение сопряжено с риском и принимается на фоне некоторого уровня неопределенности. По этой причине возможна ситуация, когда решение вовсе не может быть принято.

РЕЗУЛЬТАТЫ ИССЛЕДОВАНИЯ

Для минимизации уровня неопределенности при принятии управленческих решений авторами разработан следующий инструментарий.

Для моделирования процессов принятия решений в условиях неопределенности и разработки инструментария предлагается ввести функцию нео-пределенности?(S):/?n^[0; 1], отображающую уровень неопределенности в зависимости от тех или иных учитываемых факторовSt E S,i = 1--П, которые поддаются количественному описанию.

Задача установить явную зависимость функции неопределенности от учитываемых факторов пока не имеет решения. Однако для построения первого приближения целесообразно использовать нейронные сети. Преимущество нейросетевой модели заключается в ее гибкости по отношению к разным ситуациям и адаптации к любой области хозяйственной деятельности. При адаптации нейросетевой модели под потребности какого-либо предприятия необходимо заново обучить нейронную сеть, используя соответствующий набор данных, и при этом нет необходимости менять ее архитектуру.

Для построения модели экономической неопределенности авторами предлагается использовать нейросетевой бинарный классификатор, который в результате своей работы определяет вероятность принадлежности входных данных к некоторому классу объектов (Нехрест-Бобкова и др., 2019; Бурдина и Нехрест-Бобкова, 2020; Гафаров и Галимянов, 2018; Вакуленко и Жихарева, 2018). В качестве входных данных возможно использование вектора факторов неопределенности SeRⁿ , которые поддаются количественному описанию. Для количественного описания применимы не только статистические и аналитические методы, но и метод экспертных оценок.

Выходное значение работы нейросетевого бинарного классификатора выявляет уровень неопределенности, отвечающий заданным факторам, и выражает вероятность их принадлежности к риск-множеству.

Риск-множеством уровня « (RS_a) назовем такое множество векторов факторов неопределенности SeRⁿ , для которых значение функции неопределенности ?(5) >  a . Установление риск-множества факторов неопределенности позволяет выделить значимые факторы, порождающие неопределенность, и оказать на них влияние с целью снижения ее уровня.

Анализ неопределенности зависит от конкретной задачи, поскольку в разных ситуациях учитываются разные факторы. В качестве примера авторами рассматривается задача минимизации неопределенности при принятии решения о переходе производства компонент авиационной техники на современные инновационные композитные материалы.

Требуется определить риск-множество уровня cc =0,8, оценить уровень неопределенности при принятии данного решения и разработать рекомендации по ее минимизации.

Для упрощения и наглядности рассматривается задача с размерностью вектора факторов неопределенности n =2. Выделяются следующие факторы неопределенности:

^l – уровень увеличения цены на произведенное воздушное судно (в %);

• *^2 – срок перехода на новый материал (месяцы).

Для обучения использовались исторические данные о переходах производителей на новые композитные материалы. Учитывались срок перехода и уровень изменения себестоимости производства. При этом, чтобы увеличить объем обучающей выборки, использовались данные прогнозов.

Для исследования была выбрана полносвязная нейронная сеть прямого распространения, архитектура которой представлена на рисунке 3.

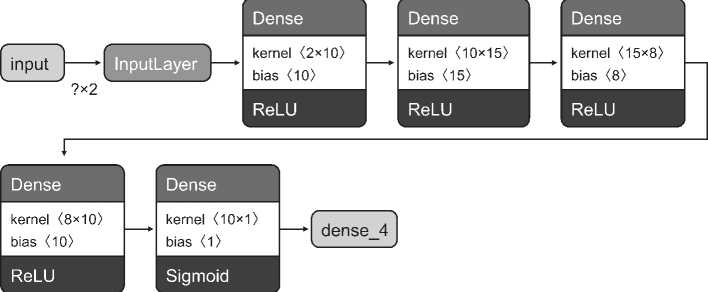
Рис. 3. Архитектура нейронной сети для моделирования неопределенности / Fig. 3. Neural network architecture for uncertainty modeling

Источник: составлено авторами на основе (Chollet, 2021).

Обучение модели проводилось при помощи оптимизатора Adam (adaptive moment estimation) с функцией потерь Binary Crossentropy. Было подобрано оптимальное число эпох, не приводящее к переобучению нейронной сети и минимизирующее функцию потерь (epochs = 50). На рисунке 4 представлен

О

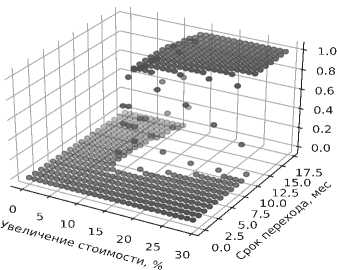
Рис. 5. Результаты нейросетевого моделирования в виде поверхности неопределенности /Fig. 5. Results of neural network modeling in the form of an uncertainty surface

график обучения нейронной сети.

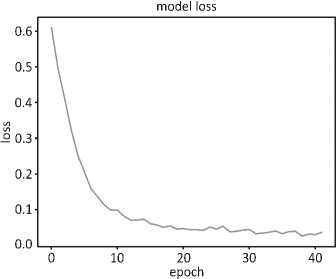
Рис. 4. График обучения нейронной сети / Fig. 4. Neural network training schedule

Источник: собственные расчеты авторов.

Точность обученной модели для двух факторов неопределенности составила 96,5 %. Добавление новых факторов неопределенности в модель требует подготовки данных и повторного обучения нейронной сети.

Созданная нейросетевая модель позволяет оценить множество неопределенности при помощи построения поверхности неопределенности в зависимости от исследуемых параметров ^1 и •$2. На рисунке 5 представлены результаты нейросетевого моделирования для поставленной задачи.

Результаты моделирования позволяют определить критические значения рассматриваемых факторов неопределенности. Для данного примера область значений параметров ^l > 10 (%) и S^ > 9 (мес.) является риск-множеством уровня ОС = 0,8. Согласно результатам моделирования, для минимизации неопределенности при принятии решения необходимо произвести переход на новый материал менее чем за 9 месяцев при увеличении себестоимости производства не более чем на 10 %.

ЗАКЛЮЧЕНИЕ

Таким образом, разработанная нейросетевая модель позволяет производить количественную оценку уровня неопределенности, что может послужить основой для выработки рекомендаций по принятию управленческих решений. Преимущества такого подхода по сравнению с аналитическими методами – гибкость и масштабируемость модели, быстрая адаптация к различным субъектам хозяйственной деятельности. Среди недостатков можно выделить зависимость от обучающей выборки, поскольку сбор необходимого для разработки адекватной нейросетевой модели объема данных является трудоемкой задачей. Отмечается, что нейронные сети позволяют решать задачи, которые сложно реализуемы классическими методами математического моделирования.