Моделирование неполных покрытий отрезка на основе сумм элементов верхних отсечений пирамиды Паскаля

Кузьмин О. В., Стрихарь М. В. Моделирование неполных покрытий отрезка на основе сумм элементов верхних отсечений пирамиды Паскаля // Вестник Бурятского государственного университета. Математика, информатика. 2024. № 3. С. 56–70.

Вводные замечания

При моделировании различных процессов и/или исследовании тех или иных явлений мы часто обращаемся к важному разделу дискретной математики, каким является комбинаторика. В вопросах анализа и хранения данных, создании и оптимизации алгоритмов их обработки возникают все новые и новые комбинаторные числа и последовательности. Все они со временем аккумулируются в онлайн-энциклопедии целочисленных последовательностей (англ. «The on-line encyclopedia of integer sequences», сокращенно OEIS) [9] , которую в 1964 г. основал Нил Слоун. Занимаясь вопросами исследования самих последовательностей было замечено, что многие из них обладают схожими свойствами, а значит могут представлять собой числовые классы или системы [1 , 5 , 6] . Так в 1993 г. О. В. Кузьмин предложил получать и изучать комбинаторные объекты при помощи многоуровневой структуры обобщенной пирамиды Паскаля, которая состоит из числовых слоев со схожими характеристиками [2] . Данная работа является продолжением исследования сечений пирамиды Паскаля и полных покрытий отрезка [4] , рассматриваются верхние отсечения пирамиды Паскаля и неполные покрытия отрезка. Определяются количество неполных покрытий отрезка, рекуррентные соотношения и производящие функции, которым удовлетворяют эти числа. В частных случаях получены известные числовые последовательности.

• 1    Полные и неполные покрытия отрезка

Полным ( m ; m i , m 2 , m 3 ) -покрытием отрезка длины m тремя отрезками, длины которых равны m 1 , m 2 и m 3 называем [4] полное заполнение длины m исходного отрезка длинами m 1 , m 2 , m 3 меньших отрезков. Перекрытие допускается только в граничных точках. При этом оговариваем, что m i <  m 2 <  m 3 , m, m i , m 2 , m 3 G N = { 1 , 2 , 3 ,... } и в случае совпадения двух или всех трех длин покрывающих отрезков, полагаем их разных цветов и граничные точки тогда оставляем неокрашенными. Таким образом различными будут те покрытия, которые отличаются либо составом покрывающих отрезков, либо их порядком.

В отличие от полного (m; mi,m2,mз)-покрытия отрезка, неполным (m; mi, m2, m3)-покрытием отрезка длины m тремя отрезками, длины которых равны m1 , m2 и m3 будем называть неполное правостороннее заполнение длины m исходного отрезка длинами mi, m2, m3 меньших отрезков, то есть слева и только слева может остаться непокрытая область размера от 0 до m включительно. Перекрытие аналогично допускается только в граничных точках (рис. 1). При этом mi < m2 < m3, m,mi,m2,m3 G N = {1, 2, 3,...} и в случае совпадения двух или всех трех длин покрывающих отрезков, полагаем их разных цветов, граничные точки в этом случае оставляем неокрашенными (рис. 2). Таким образом различными будут те неполные (m; mi, m2, m3 )-покрытия, которые отличаются либо размером непокрытой области, либо составом покрывающих отрезков, либо их порядком и в число неполных (m; mi, m2, mз)-покрытий отрезка обязательно будет входить полное (m; mi, m2, m3 )-покрытие отрезка, получающееся при нулевой длине непокрытой области.

	m i	m 2	m 3
		m

Рис. 1. Неполное (m; mi, m2, mз)-покрытие, все длины покрывающих отрезков mi, m2 и m3 различны

<>Ч)            1>- ■ ■■■■■■<)

m i        m 2               m 3

m

Рис. 2. Неполное ( m ; m i , m 2 , m 3 ) -покрытие, длины m 2 и m 3 совпадают

Замечание 1. Если НОД ( m i , m 2 , m3) = д = 1 , то есть наибольший общий делитель чисел m i , m 2 и m 3 не равен единице, тогда и число полных и число неполных ( m ; m i , m 2 , m з ) -покрытий совпадает соответственно с числом полных либо неполных ( k ; m i /д, m 2 / д, m 3 /д)- покрытий отрезка в случае m = дк, k G N . В том случае, когда m = дк, к G N , не найдется полного ( m ; m i , m 2 , m 3 ) -покрытия, являющегося обязательным вариантом для перечисления всех неполных ( m ; m i , m 2 , m з ) -покрытий [4] . Поэтому в дальнейшем будем рассматривать только вариант, когда НОД ( m i , m 2 , m3) = 1 .

• 2    Базисные понятия и соотношения

Пирамида Паскаля — это бесконечная трехгранная пирамидальная структура, элементы которой для целых неотрицательных n, k, l удовлетворяют рекуррентным соотношениям [2] :

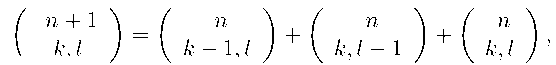
n + 1 k, l n  nn

k - 1 ,1         k,i - 1         k,i

то есть каждый внутренний элемент пирамиды Паскаля, представляет собой сумму трех элементов, расположенных над ним, при выполнении граничных условий:

(q°₀) = 1 ; k,li) = 0 , если min( n, k,l,n — k — 1 ) <  0 .

Числа k^ = k i ( П — _k-l) называются триномиальными коэффициентами и для них справедливы равенства:

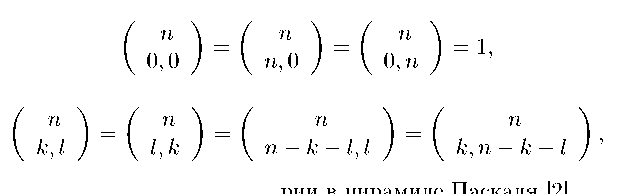
n

n

0 , 0

n, 0

n

n

n n — k — l, l

n k, n — k — l k, l l, k указывающие на три оси симметрии в пирамиде Паскаля [2].

Для нахождения количества всех неполных покрытий отрезка поместим пирамиду Паскаля в прямоугольную декартову систему координат в пространстве, при этом совместим вершину пирамиды с точкой начала координат O (0;0;0) , числа n отметим по оси абсцисс On, k — по оси ординат Ok , l — по оси аппликат Ol . Таким образом получаем биективное отображение всех элементов пирамиды Паскаля на точки ( n ; k ; l ) целочисленной решетки первого октанта с неотрицательными координатами, ограниченные плоскостями k = 0 , n = 0 и n — k — l = 0 .

Рассечем пирамиду Паскаля плоскостью, образующую углы ф 1 и ф 2 с осями Ok и Ol соответственно. Уравнение такого сечения [8] :

n + tg ф 1 • k + tg ф ₂ • l = const.

Все параллельные между собою сечения пирамиды Паскаля, заданные уравнением вида (1) , занумеруем, начиная от вершины. Предметом наших исследований являются последовательности сумм элементов таких сечений:

{ S n (tg ф 1 , tg Ф 2 ) } ,N G N ° = { 0 , 1 , 2 , 3 ,... } .

Полагаем tg фг = Pr/qr,Pr G Z,qr G N, НОД (pr,qr) = 1,r = 1,2.

В случае p r /q r >  — 1 сечения треугольные и замкнутые, уравнение (1) принимает вид [3] :

p 1       p 2           N

q i        q 2      НОК ( q i ,q 2 ) ^.

Формула для определения суммы элементов N -го плоского сечения пирамиды Паскаля в явном виде [4] :

S N

p 1 p 2 q 1 ^, q 2

qiN 1 Г q2N 1 i q⁽pi⁺qi⁾J Lq(P2+q2)J      / n

XX i=0       j=0

pi i qi i, j

P 2 j q 2 j

где q = НОК ( q i , q 2) — наименьшее общее кратное чисел q i и q 2 .

Продолжая исследование, найдем сумму элементов N -го плоского сечения пирамиды Паскаля и всех элементов пирамиды, расположенных над ним. Такой конечный массив элементов пирамиды Паскаля, ограниченных снизу плоскостью сечения, заданного уравнением вида (2) , будем называть N -ым верхним отсечением [3] пирамиды Паскаля.

Зная, что сумма элементов N -го плоского сечения пирамиды Паскаля вычисляется по формуле (3) , получаем соотношение для вычисления суммы элементов N -го верхнего отсечения пирамиды Паскаля:

U N

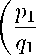
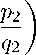
h qir i h q2 ^r i

N Lq⁽Pi⁺qi⁾J Lq⁽P2⁺q2)J

=X X  X r=0   i=0       j=0

r    P i 2 P 2 2

- i- j q     qi q2

i, j

3 Количество полных и неполных покрытий

В предыдущей нашей работе [4] было доказано, что количество полных ( m ; m i , m 2 , m 3 ) -покрытий отрезка задается равенством:

m1

ml m3

h _m i h _m i_{- i}

Lmij Lm2.|     /

= X X i=0 j=0

m - f m i — i — f m 2 — 1^1 j\       .

m3   Vm3    J    Vm3    7 j ,m G N i, j

для чего мы полагали в выражении (3) :

p l = m l - 1 p ² = m ² - 1 .

q 1    m 3      q 2    m 3

Рассмотрим теперь сумму элементов m-го верхнего отсечения пирамиды Паскаля следующего вида

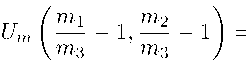
m

h _r ih _r i m m ₁   m ₂

= XX X

r =0 i =0    j =0

m2 — 1 j            _ m3         , m ∈ N (6)

и докажем, что она задает количество всех неполных ( m ; m i ,m 2 ,m 3 ) -покрытий отрезка.

Теорема 1. Количество всех неполных ( m ; m ± ,m 2 , m3)-покрытий равно сумме (6) элементов m-го верхнего отсечения пирамиды Паскаля.

Доказательство.

При рассмотрении всех возможных неполных покрытий отрезка длины m имеем следующие варианты:

• 1)    область длины m полностью не покрыта;

• 2)    область длины ( m — 1) , находящаяся слева, не покрыта, область длины 1, находящаяся справа, полностью покрыта;

• 3)    область длины ( m — 2) , находящаяся слева, не покрыта, область длины 2, находящаяся справа, полностью покрыта;

...

m — 1 ) область длины ( m — ( m — 1)) = 1 , находящаяся слева, не покрыта, область длины m — 1 , находящаяся справа, полностью покрыта;

• m) область длины ( m — m ) = 0 , находящаяся слева, не покрыта, область длины m , находящаяся справа, полностью покрыта.

Поскольку количество полных ( m ; m 1 ,m 2 ,m з ) -покрытий задается равенством (5) , то число неполных ( m ; m 1 ,m 2 ,m з ) -покрытий равно:

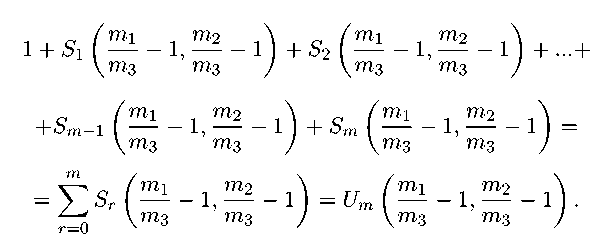
m

+

Теорема доказана.

Замечание 2. Поскольку в вершине пирамиды Паскаля находится число

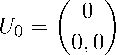
= 1 ,

то оно естественным образом определяет для нашего исследования количество неполных (0; m i , m 2 , m з ) -покрытий отрезка нулевой длины. Поэтому далее полагаем, что m 6 N g , т.е. длина покрываемого отрезка условно может быть неотрицательным целым числом.

4 Рекуррентные соотношения

{U m } = {Um (m 3

- 1 , m 3 - О},

Рассмотрим последовательность m 6 Ng неполных (m; mi,m2,mз)-покрытий отрезка.

Теорема 2. Последовательность чисел {Um}, m 6 N, удовлетво- ряет рекуррентному соотношению

U m — Um - m i + U m — m 2

+ U m — m ₃ + ¹

с начальными условиями

U g — U i — U 2 — ... — U m i — 1 — 1;                 (9)

U _m , при m — m i , ...,m _m 2 _— i , удовлетворяют соотношениям

U m — ^U m — m i + ^{1;                     (10)}

U _m , при m — m 2 , ...,m m _{3 —} i , удовлетворяют соотношениям

U m — ^U m — m i + ^U m — m 2

+ 1 .

Доказательство.

Рассмотрим рекуррентное соотношение (8) . В нем указана сумма способов, которыми можно покрыть отрезок длины m >  m 3 . Очевидно, есть только четыре возможности неполного ( m ; m i , m 2 , m з ) -покрытия отрезка. В первом случае осуществляется неполное ( m - m i ; m i , m 2 , m 3 ) -покрытие, после чего добавляется справа отрезок длины m 1 . Во втором случае производится неполное ( m — m 2 ; m i , m 2 , m з ) -покрытие и добавляется справа отрезок длины m 2 . В третьем случае выполняется неполное ( m — m 3 ; m _i , m 2 , m з ) -покрытие и добавляется справа отрезок длины m 3 . В четвертом случае отрезок остается полностью непокрытым.

О. В. Кузьмин, М. В. Стрихарь. Моделирование неполных покрытий отрезка на основе сумм элементов верхних отсечений пирамиды ...

Начальные условия (9) свидетельствуют о том, что если длина покрываемого отрезка меньше минимального покрывающего, то невоз- можно осуществить полное покрытие этого отрезка, а значит отрезок оставляется полностью непокрытым.

В соотношениях (10) сказано, что в случае, когда длина покрываемого отрезка достигает длины m 1 наименьшего покрывающего отрезка, но меньше длины m 2 второго по величине отрезка, то неполное ( m ; m i , m 2 , т з ) -покрытие можно выполнить только отрезками длины m 1 , осуществив сначала неполное ( m — m 1 ; m ₁ ,m ₂ ,m з ) -покрытие, а затем добавив справа отрезок длины m 1 , либо оставить отрезок полностью непокрытым.

Соотношения (11) показывают, что в случае, когда длина покрываемого отрезка достигает длины m 2 второго по величине отрезка, но меньше длины m 3 максимального по величине покрывающего отрезка, то неполное ( m ; m i , m 2 , m з ) -покрытие можно выполнить только отрезками длины длины m 1 и m 2 , осуществив сначала неполные ( m — m i ; m i , m 2 , m з ) -покрытие и ( m — m 2 ; m i , m 2 , m з ) -покрытие, а затем добавив справа соответственно отрезки длины m 1 и m 2 , либо отрезок остается полностью непокрытым.

Теорема доказана.

Поскольку пирамида Паскаля имеет три оси симметрии, то получаем следствие из теорем 1 и 2, которое позволяет производить вычисление суммы элементов верхнего отсечения по любой из шести представленных формул.

Следствие. Для натуральных чисел m 1 , m 2 , m 3 , при условии что НОД ( m i , m 2 , m3) = 1 , справедливы равенства:

m 1      m 2 U m U3    1 , m 3   11 =   Um ( m l — 1 , m 3 — 1 ) m m 2     , m 2 =   Um ( m 2 — 1 , m 3 — 1 J m m 1     , m 1

m 2      m 1 =   U m lm3    1 , m 3    11    = =   Um ( m 3 — 1 , m l — 1 )    =     (12) m  m 2     , m 2 =   Um ( m 3 — 1 , m 2 — 1 ) . m  m 1     , m 1

5 Производящие функции

Если последовательности чисел { U m } , m G N o , сопоставить формальный степенной ряд, то становится возможно нахождение производящей функции этих чисел.

Теорема 3. Для последовательности чисел {U m }, m G N o производящей функцией является

F U ^{( x )} =

(1 — x )(1 — x m i

— x m 2 — x m 3 ) .

Доказательство.

Зная, что последовательность чисел {U m }, m G N o удовлетворяет соотношениям (8) — (11) , согласно теореме 2, представим рекуррентное соотношение (8) в более удобном виде

^U m + m 3 — ^U m + m 3 — m i + ^U m + m 3 — m 2 + U m + 1 .

Выполним почленное умножение этого соотношения на x m + ^m 3 и просуммируем по m в пределах от нуля до бесконечности:

∞

∞

Е ТТ ,   ~ ^m+ m3 ₌ ~^m 1

m + m 3 x     — x

^U m + m 3 - m i

x m + ms - mi

+

∞     ∞∞

+ x ^m 2 X U m + m 3 - m 2 x ^{m + m} 3 ^{— m 2} + x m ³ X U m X m + X x m ⁺ m ³ . m =0                          m =0         m =0

Полагая

∞

Fu(x) — X Umxm, m=0

получаем:

m3 — 1                /         m3—mi-1\

Fu (x) - X Umxm — xmi Fu (x) - X Umxm + m=0             \          m=0/

(m3—m2 — 1      \м

F u ( x ) -   X U m x^mj + x m ³ F u ( x ) + X x m .

m=0       /

Раскроем скобки и выполним перенос слагаемых:

m 3 — 1                            m 3 — m i — 1

Fu(x) - X Umxm — xm1 Fu(x) - xm1  X m=0

+xm2 Fu(x) - xm2  X  Umxm + xm3Fu (x) + X xm, m=0

Fu(x) - xm1 Fu (x) - xm2 Fu (x) - xm3Fu (x) — m3 —1             m3—mi-1             m3—m2 —1

• — X Umxm - xm1 X Umxm - xm2 X Umxm + X xm. m=0              m=0               m=0

Согласно начальным условия (9) и соотношениям (10) — (11) , выпишем отдельно правую часть последнего равенства и выполним для нее преобразования:

m3 — 1             m3—mi — 1             m3—m2 — 1м

X Umxm - xmi  X Umxm - xm X Umxm + X xm — m=0              m=0               m=0

' mi-1           m2 —1

X U m X m + X U m X m + X U m X m

, m=0         m=mi m2 —m1 —1          m3 —m1 —1                m3 —m2 —1

X UmXm + X  UmXm - xm2  X UmXm + m=0          m=m2—mi      /

(m       m2 —1      m3 —1\

X xm - X xm - X xm = m=mi     m=mi     m=m2/ mi—1       m2 —1

= X Xm + X UmXm + X UmXm-m=0     m=mi m2—mi—1              m3—mi—1              m3—m2—1

• - X   U m X ^{m + m} 1 — X   U m X m + m ¹ — X   U m X m + m ² +

m=0             m=m2—mi m        m2 —1

+ X Xm - X Xm - X Xm = m=mi     m=mi mi—1       m2 —1

= X Xm + X UmXm + X UmXm-m=0     m=mi

-

m 2 — 1

X Um-m1xm m=mi

-

m 3 — 1

Um-m1xm m=m2

-

m 3 — 1

X Um—m2 Xm + m=m2

m        m2 —1

+ X Xm - X Xm - X Xm = m=mi     m=mi mm

= X Xm + X (Um - Um—mi - 1) Xm + m=0

m 3 — 1

+ ^X ( U m

-

U m - m 1

-

U m - m 2

-

1) X m

m = m 2

m 2 — 1           m 3 — 1

= ^+ X 0 • Xm + X 0 • Xm = m=mi        m=m<2

Возвращаясь к тому моменту, когда была выписана отдельно правая часть, получаем:

F u (x)(1 - X ^{m i} - X m ² - X m ³ ) =

1 - X,

то есть производящая функция последовательности {U m } , m G N o , имеет вид:

F U ^{( x )} =

(1 - x)(1 - xm1 - xm2 - xm3), что и требовалось доказать.

• 6 Известные числовые последовательности

• 6.1    Суммы чисел Якобсталя

В первых трех столбцах таблицы 1 приведены 10 троек значений чисел m i , m 2 и m 3 неполных ( m ; m 1 ,m 2 ,m з ) -покрытий отрезка.

В четвертом столбце — соответствующие последовательности U _m , m G N o количества неполных ( m ; m i , m 2 , m з ) -покрытий отрезка длины m. Здесь первое число показывает количество неполных покрытий отрезка длины 0, второе число отвечает за количество покрытий отрезка длины 1 и так далее.

В пятом и шестом столбце указаны углы верхних отсечений пирамиды Паскаля, в которых были выявлены эти последовательности, а в последнем столбце приведены номера полученных последовательностей в [9] . Символ * рядом с номером последовательности был добавлен в случаях, когда полученные нами числа совпали с указанными в [9] , начиная с определенного номера.

m i	m 2	m 3	U m ,m G N o	tg Ф 1	tg ф 2	№ в [9]
1	2	2	1, 2, 5, 10, 21, 42, 85, 170, 341, ...	1	1	A000975*
1	1	1	1, 4, 13, 40, 121, 364, 1093, 3280, ...	0	0	A003462*
1	3	3	1, 2, 3, 6, 11, 18, 31, 54, 91, 154, ...	2	2	A003479
1	2	3	1, 2, 4, 8, 15, 28, 52, 96, 177, ...	2	1	A008937*
2	3	4	1, 1, 2, 3, 5, 7, 11, 16, 24, 35, ...	1	1 / 2	A023435*
1	1	2	1, 3, 8, 20, 49, 119, 288, 696, ...	— 1 / 2	— 1 / 2	A048739
2	2	3	1, 1, 3, 4, 8, 12, 21, 33, 55, 88, ...	— 1 / 3	— 1 / 3	A052952
1	1	3	1, 3, 7, 16, 36, 80, 177, 391, 863, ...	- 2 / 3	- 2 / 3	A077852
2	3	3	1, 1, 2, 4, 5, 9, 14, 20, 33, 49, 74, ...	1 / 2	1 / 2	A077882*
1	3	4	1, 2, 3, 5, 9, 15, 24, 39, 64, 104, ...	3	2	A097083

Таблица 1. Неполные покрытия отрезка длины m и некоторые известные комбинаторные числа

Рассмотрим подробнее некоторые последовательности из таблицы 1.

В первой строке таблицы 1 показаны неполные ( m ; 1 , 2 , 2) -покрытия при m 1 = 1 , m 2 = m 3 = 2 . Поскольку m 2 = m 3 , то покрывающие отрезки длины 2 окрашены разными цветами. При этом цвета отрезков длин m 1 и m 2 совпадают.

О. В. Кузьмин, М. В. Стрихарь. Моделирование неполных покрытий отрезка на основе сумм элементов верхних отсечений пирамиды ...

Количества неполных ( m ; 1 , 2 , 2) -покрытий U m , m G N o образуют последовательность чисел 1, 2, 5, 10, 21, 42, 85, 170, 341, 682, 1365, . . . , и выявляются при суммировании элементов верхних отсечений пирамиды Паскаля, для которых один из шести вариантов расположения, согласно (6) и (12) , будет при tg ф 1 — tg Ф 2 = 1 .

Соотнеся полученные числа с указанными в [9], получаем последовательность сумм чисел Якобсталя [7], указанной под номером A000975, которая определяется при помощи рекуррентного соотношения am — am-1 + 2 • am-2 + 1, a0 — 0, al — 1, a2 — 2, со сдвигом на единицу относительно Um, т.е. Um — am+i.

Число неполных ( m ; 1 , 2 , 2) -покрытий при этом вычисляется по формуле (6) :

m [ 2 ] [ 2 ] ^-i

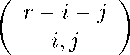
Um (1.1) — EEE r=0 i=0 j=0

и удовлетворяет, согласно (8) — (11) , рекуррентному соотношению

U m — U m - 1 + 2 U m - 2 + 1 ,S o — 1 , S i — 2 .

Соответствующая производящая функция, согласно (13) , имеет вид

F U ^{( x ) —} (1 - x )(1 - x - 2 x 2 ) .

• 6.2    Суммы степеней числа 3

Во второй строке таблицы 1 показаны неполные ( m ; 1 , 1 , 1) -покрытия при m i — m 2 — m 3 — 1 . Поскольку длины всех трех покрывающих отрезков совпадают, то окрашиваем их тремя разными цветами.

Количества неполных ( m ; 1 , 1 , 1) -покрытий U _m , m G N o образуют последовательность чисел 1, 4, 13, 40, 121, 364, 1093, 3280, 9841, . . . , и выявляются при суммировании элементов верхних отсечений пирамиды Паскаля с горизонтальными плоскими основаниями, для которых, согласно (6) и (12) tg ф 1 — tg Ф 2 — 0 .

Соотнеся полученные числа с указанными в [9] , получаем последовательность сумм степеней числа 3, указанной под номером A003462:

am — (3m - 1)/2, со сдвигом на единицу относительно Um, т.е. Um — am+i.

Число неполных ( m ; 1 , 1 , 1) -покрытий вычисляется по формуле (6) :

m r r - i

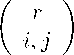
Um (0,0) — EEE r=0 i=0 j=0

и удовлетворяет, согласно (8) — (11) , рекуррентному соотношению

U m = 3 U m - 1 + 1 ,S 0 = 1 .

Производящая функция, согласно (13) , имеет вид

F U ⁽ x ) = (1 - x )(1 - 3 x ) .

• 6.3    Суммы чисел Трибоначчи

Четвертая строка таблицы 1 содержит информацию по неполным ( m ; 1 , 2 , 3) -покрытиям отрезками разных длин одного цвета.

Количества неполных ( m ; 1 , 2 , 3) -покрытий U m , m G N o образуют последовательность чисел 1, 2, 4, 8, 15, 28, 52, 96, 177, 326, 600, . . . , и выявляются при суммировании элементов верхних отсечений пирамиды Паскаля, для которых, согласно (6) и (12) один из шести вариантов расположения имеем при tg ф 1 = 1 , tg Ф 2 = 2 .

Соотнеся полученные числа с указанными в [9] , получаем последовательность сумм чисел Трибоначчи, указанной под номером A008937, которая определяется соотношением:

am — 1 + am-1 + am-2 + am-3, a0 — 0, al — 1, a2 — 2, со сдвигом на единицу относительно Um, т.е. Um — am+i.

Число неполных ( m ; 1 , 2 , 3) -покрытий вычисляется по формуле:

m [ 2 ] [ 3 ] i /

- i - 2 j

i, j

U m (1 , 2) — XXX (r r =0 i =0 j =0

и удовлетворяет, согласно (8) — (11) , рекуррентному соотношению

U m ^— U m - 1 + U m - 2 + ^U m - 3 + ^{1 ,U} 0 ^— 1 , ^U 1 ^{— 2 ,U} 2 ^— 4 .

Производящая функция, исходя из (13) , имеет вид

U^{U ( x )}   (1 — x )(1 — x — x ² — x ³ ) .

Заключительные положения

В данной работе были исследованы некоторые геометрические свойства пирамиды Паскаля и доказано, что сумма элементов верхних отсечений пирамиды Паскаля равна количеству неполных покрытий соответствующего ей отрезка. Найдены формула вычисления количества неполных покрытий отрезка в явном виде, рекуррентные соотношения и производящие функции для этих чисел. Результаты, представленные в данной работе, могут быть использованы в построении моделей машинного обучения как для анализа больших объемов данных, так и при их проектировании. Подсчитав количество возможных комбинаций данных, либо различного рода связанных с ними событий, можно определять требования к хранению данных и прогнозировать их изменения для принятия более обоснованных решений и оптимизации производственных процессов. Дальнейшее исследование предполагает рассмотрение различных обобщений пирамиды Паскаля и их частей.