Моделирование непрерывного процесса свободно-радикальной сополимеризации бутадиена со стиролом методом Монте-Карло

Обширную группу нефтехимической продукции составляют синтетические каучуки, которые представляют собой полимеры, способные перерабатываться в процессе вулканизации в резину. В настоящее время производится широкий ассортимент синтетических каучуков, отличающихся потребительскими свойствами, что напрямую зависит от используемых мономеров: бутадиен, стирол, изопрен и др. Их сочетание и способ полимеризации определяет конечные свойства получаемого продукта и его назначение.

Бутадиен-стирольные синтетические каучуки являются одними из самых распространённых крупнотоннажных каучуков общего назначения. В основе промышленного производства лежит процесс низкотемпературной свободно-радикальной сополимеризации бутадиена со стиролом в эмульсии. Изучение этого процесса становится возможным при построении математической модели. В свою очередь, моделирование позволит прогнозировать свойства и модифицировать качественные показатели получаемого продукта, что является актуальной задачей на сегодняшний день.

• 1.1    Материалы и методы исследований

Предварительно необходимо выписать кинетическую схему процесса сополимеризации, при этом будем полагать, что реакционная способность активного центра растущей цепи определяется природой концевого звена. Кинетическую схему процесса составляют следующие стадии: распад инициатора

I - - 2 R , инициирование активных центров р + м^Р k^ >  рР

R + M         > PA (в), в (в), рост цепи

• р“ + мР__ kp^ >  рР

Pn, m + M           - Pn+A ( Р), m+B ( Р), передача цепи на регулятор

P“,m + ^ -—- Qn , m + R , обрыв цепи по механизму рекомбинации

P a ,_pp    k^ q

• ¹    n , m ^{+ 1} r , q          ^- Q n + r , m + q ,

обрыв цепи по механизму диспропорционирования P“ ^pP^p k^dop > 0 + 0 .

n,m rq,q                 n,m xqr,q где a, Р = 1,2; M1, M2 — мономеры первого и второго типа (бутадиен и стирол); P^m и Qn m

—

активные и неактивные цепи полимера длиной m + n, состоящие из m звеньев мономера M1 и n звеньев мономера M2 , оканчивающиеся мономером M “; ki, kp, kreg, kd, kr — константы элементарных стадий инициирования, роста, передачи цепи, диспропорционирования и рекомбинации соответственно; A(Р)={1, если Р = 1; иначе 0}; B(Р) = {1, если Р = 2; иначе 0}.

Ранее в работе [1] был рассмотрен алгоритм моделирования периодического процесса сополимеризации бутадиена со стиролом, основанный на методе Монте-Карло. Но производство бутадиен-стирольного каучука представляет собой непрерывный процесс, протекающий одновременно в нескольких аппаратах, объединённых в каскад. Это связано с повышением производительности, стабильными показателями получаемого продукта и экономической эффективностью.

При моделировании периодического по-лимеризационного процесса всё частицы системы на протяжении всего времени находятся в одном реакторе. В этом случае каждая реакция характеризуется временем моделирования, которое рассчитывается по формуле:

А 1 1

^А t = „ ’^И' ' , (1)

Rr sum p где Rsum — сумма скоростей возможных элементарных реакций кинетической схемы процесса, rp — случайное число, сгенерированное на отрезке [0,1]. Но в случае непрерывного процесса стоит говорить о некотором среднем времени пребывания как о некоторой случайной величине, которая характеризуется вероятностной функцией распределения [2].

Согласно [3], вероятность того, что частица проводит время от t до t + dt в текущем реакторе, равна p ( t ) dt , но так как рассматриваемые полимеризаторы представляют собой реакторы идеального смешения непрерывного действия, то для них величина p ( t ) рассчитывается по формуле:

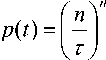
t n - 1      - nt

----------e ^т , ( n - 1)!

где n — количество реакторов в системе, т — среднее время пребывания реакционной смеси в одном реакторе (ч).

На рисунке 1 изображено распределение частиц реакционной смеси по времени пребывания для батареи из 12 полимеризаторов объёмом V = 10.8 м³ c объёмной скоростью потока C f = 9.5982 м³/ч. В этом случае среднее время пребывания реакционной смеси в одном полимеризаторе равно 1.125 ч.

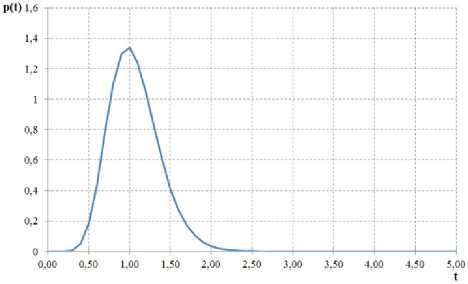
Рисунок 1. Распределение по времени пребывания в каскаде из 12 реакторов

Figure 1. Residence time distribution in the cascade of 12 reactors.

Таким образом, для моделирования непрерывного процесса полимеризации, проводящегося в каскаде реакторов идеального смешения, необходимо каждую частицу системы (молекулу, макромолекулу) дополнительно характеризовать временем пребывания в реакторе, которое определяется с использованием распределения (2). Для этого отрезку времени от 0 до t max подбирали шаг разбиения dt , чтобы сумма вероятностей для каждого варианта времени пребывания была равна единице.

После этого необходимо сгенерировать случайное число r p e [0,1] и подобрать такое значение порядкового номера f, чтобы существовало неравенство:

f - i f

£ P⁽⁽f ^- 1) • dt ) <  r p < 2 P ⁽ f • dt )• ⁽³⁾ i = 1 i = 1

Следовательно, в результате розыгрыша выбранной частице соответствует время пребывания J • dt [4].

Тогда для процесса, которому соответствует среднее время пребывания реакционной смеси 1.125 ч, таким отрезком времени является отрезок от 0 до 5 ч с шагом 0.1 ч.

Алгоритм моделирования непрерывного процесса сополимеризации бутадиена со стиролом можно представить в виде последовательности шагов, при этом учитывается, что каждый час в первый реактор добавляется порция реакционной смеси, соответствующая производственной рецептуре процесса.

Шаг 1. Зададим объём и характеристики подаваемой порции реакционной смеси, предварительно рассчитав количество молекул каждой составляющей смеси: бутадиен M¹ , стирол M² , инициатор I и регулятор S . Также необходимо задать технологические параметры процесса:

объём реактора V, количество реакторов m , объёмную скорость потока C f и порядковые номера полимеризаторов, в которые подаётся регулятор.

Шаг 2. Преобразуем константы скоростей элементарных реакций:

k = k для реакций первого порядка;

~ =__k__ для реакций второго порядка (V -V • Na объём реактора, NA – постоянная Авогадро).

Шаг 3. Вычислим скорость каждой реакции кинетической схемы R i для реактора с порядковым номером j :

~

Ri= k^Xa • Xb , где ki – константа скорости i -й реакции, в ко- торой участвуют реагенты A и B ; XA , XB – концентрации реагентов (количество молекул). Посредством их суммирования получим общую скорость реакции:

Rsum = R + R2 + ... + Rn, где n – число элементарных реакций кинетической схемы процесса.

Шаг 4. Вычислим вероятность p i осуществления каждой реакции в данный момент времени:

R

• p, =   —, i = 1.. n.

i sum

Очевидно, что p 1 + p 2 + .. . + p_n = 1

Шаг 5. Сгенерируем равномерно распределённое случайное число r _p на отрезке от 0 до 1 и подберём такое значение порядкового номера реакции в кинетической схеме процесса f , чтобы существовало неравенство:

k - 1               k

• У, P i <  r < y Pi . i = 1                  i = 1

Следовательно, в результате имитационного выбора в реакторе с порядковым номером j до лжна произойти реакция под индексом f ( f = 1, n ).

Шаг 6. Для выбранной реакции рассчитаем время её моделирования A t j согласно формуле (1), а для каждой образованной или оборванной в результате шага 5 частицы определим время её выхода из текущего реактора t ex :

teix = t + tdm, где t – текущее время моделирования процесса с его начала, tdm – время пребывания молекулы в текущем реакторе, вычисленное согласно распределению (2).

Шаг 7. Повторим последовательность действий с шага 3 по шаг 6 для каждого реактора каскада ( j = 1, m )

Шаг 8. Изменим общее время моделирования, увеличив его на минимальное время моделирования реакции во всех полимеризаторах:

t = t + min A t j .

• j = 1, m

Шаг 9. Для каждого реактора каскада переведём в следующий реактор всё молекулы, время выхода которых меньше общего времени протекания процесса. После этого возвратимся к шагу 3.

Шаг 10. Продолжая рассуждения и повторяя последовательность действий с шага 3 по шаг 9, выстроим всю схему моделирования процесса.

Построенная модель даёт возможности для исследования характеристик бутадиен-стирольного сополимера. При этом информация о состоянии образующегося продукта может быть получена как на выходе из каждого реактора, так и при достижении необходимых значений конверсии.

• 1.2 Результаты и обсуждение

На основе разработанного алгоритма создан программный комплекс в среде программирования Visual Studio на языках C# и Visual C++. Он позволяет проводить вычислительные эксперименты по моделированию непрерывного процесса сополимеризации бутадиена со стиролом в каскаде реакторов идеального смешения. Программный комплекс даёт возможность решать прямую задачу определения молекулярно-массовых и вязкостных характеристик получаемого продукта, а также исследовать композиционное распределение образующегося сополимера.

При проведении вычислительного эксперимента был исследован процесс сополимеризации бутадиена со стиролом при следующих технологических параметрах ведения процесса и производственной рецептурой порции реакционной смеси: ─ нагрузка на батарею по мономерам: 3,0 т/ч (бутадиен 70 мас. ч., стирол – 30 мас. ч.);

─ дозировка инициатора (гидроперекись пинана): 0,048 мас. ч.;

─ дозировка регулятора (трет-додецил меркаптан): 0,26 мас. ч. – первая точка (1 полимеризатор), 0,02 мас. ч. – вторая точка (7 полимеризатор);

─ соотношение вода/мономеры = 220,8 / 100;

─ рабочий объём полимеризатора V = 10,8 м³ ; ─ число полимеризаторов: 12;

─ объёмная скорость потока C f = 10,1432 м³/ч .

─ время нахождения реакционной смеси в одном полимеризаторе θ = V / C f = 1,065 ч .

Таблица 1.

Данные производственного эксперимента

Table 2.

Data of production experiment

Номер реактора Number of reactor	Конверсия мономе-ров,% Conversion of mono-mers,%	Характ. вязкость, дл/г Intrinsic viscosity, dl/g	Содержание связанного стирола,% Content of bound sty-rene,%
4	42,0	1,13	20,8
5	60,5	1,23	21,5
9	76,6	1,52	23,3
12	82,0	1,74	24,7

На рисунке 2–4 изображено поведение конверсионной кривой и зависимостей характеристической вязкости от порядкового номера реакторов и конверсии мономеров. Результаты были получены по итогам моделирования 15 и 30 часов ведения процесса и удовлетворительно согласуются с экспериментальными данными.

Поведение кривой характеристической вязкости связано с расходом регулятора (рис. 5). Основная часть регулятора (более половины порции) расходуется в первом и втором реакторах, что существенно замедляет рост характеристической вязкости. Дополнительная подача регулятора во вторую точку в седьмой реактор способствует повторному замедлению бурного роста характеристик продукта. В дальнейшем регулятор расходуется полностью, чему и соответствует резкий рост молекулярной массы, а соответственно и характеристической вязкости получаемого сополимера.

Характер изменения молекулярной массы образующегося бутадиен-стирольного сополимера отображает зависимость коэффициента полидисперсности от номера полимеризатора в каскаде (рис. 6). По итогам моделирования 30 часов ведения процесса значения коэффициента полидисперсности меняются от 2 ед. в первом реактора до 5.5 ед. в последнем реакторе каскада, что соответствует стандартным показателям бутадиен-стирольного каучука. Точка перегиба кривой зависимости коэффициента полидисперсности от номера реактора связана с дробной подачей регулятора.

Изменение массового состава образующегося бутадиен-стирольного сополимера изображено на рис. 7: содержание бутадиена меняется с 80% в первом реакторе до 72% в последнем реакторе каскада, стирола – с 20% до 28% соответственно.

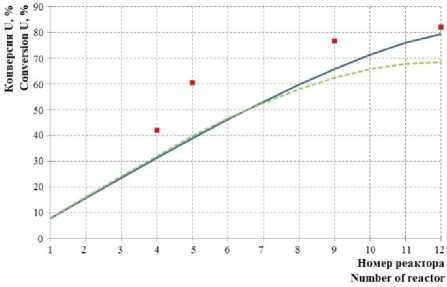
Рисунок 2. Зависимость расчётных (линия) и экспериментальных (точки) значений конверсии от номера реактора в каскаде: пунктир – 15 ч, сплошная линия – 30 ч ведения процесса

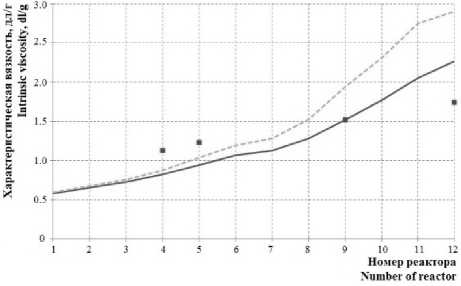
Рисунок 3. Зависимость расчётных (линия) и экспериментальных (точки) значений характеристической вязкости от номера реактора в каскаде: пунктир – 15 ч, сплошная линия – 30 ч ведения процесса

Figure 2. The dependence of the calculated (lines) and experimental (points) conversion’s values from reactor’s number in the cascade: the dotted line – 15 hours, the solid line – 30 hours conducting of the process

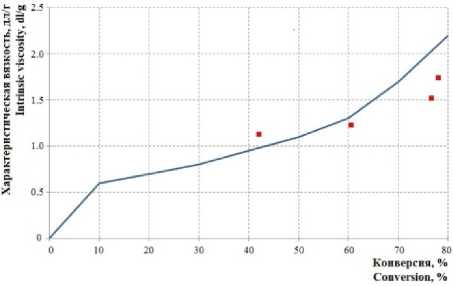
Рисунок 4. Зависимость расчётных (линия) и экспериментальных (точки) значений характеристической вязкости от конверсии мономеров

Figure 4. The dependence of the calculated (lines) and experimental (points) intrinsic viscosity’s values from conversion of monomers

Figure 3. The dependence of the calculated (lines) and experimental (points) intrinsic viscosity’s values from reactor’s number in the cascade: the dotted line – 15 hours, the solid line – 30 hours conducting of the process

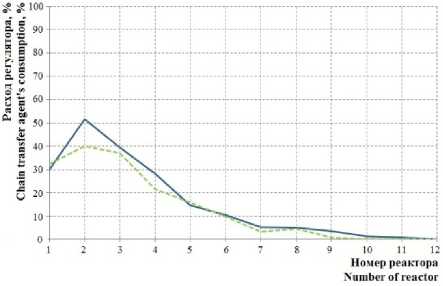
Рисунок 5. Изменение концентрации регулятора в реакторах: пунктир – 15 ч, сплошная линия – 30 ч ведения процесса

Figure 5. Changing chain transfer agent's concentration in the reactors: the dotted line – 15 hours, the solid line – 30 hours conducting of the process

Номер реактора Number of reactor

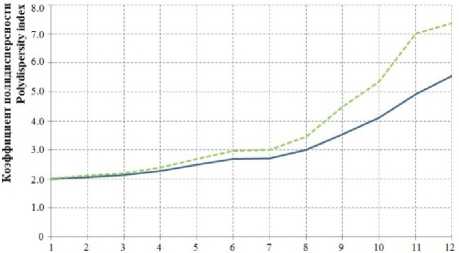
Рисунок 6. Изменение коэффициента полидисперсности образующегося сополимера в зависимости от номера реактора: пунктир – 15 ч, сплошная линия – 30 ч ведения процесса

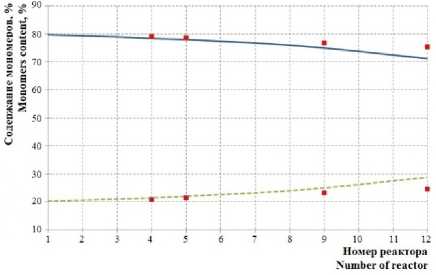
Рисунок 7. Зависимость массового содержания бутадиена (сплошная линия) и стирола (пунктир) от номера реактора (точки – экспериментальные данные)

• Figure 6.    Changing polydispersity index of the formed copolymer depending on the number of reactor: the dotted line –

15 hours, the solid line – 30 hours conducting of the process

• Figure 7.    Dependence of weight content of butadiene (solid line) and styrene (dotted line) from number of the reactor (points – experimental data)

На рисунке 8 изображена дифференциальная кривая молекулярно-массового распределения (ММР), которая демонстрирует соотношение макромолекул различной молекулярной массы в образце сополимера. При моделировании процесса сополимеризации методом Монте-Карло для построения ММР необходимо произвести численное фракционирование макромолекул образовавшегося сополимера по массе и рассчитать массовую долю каждой фракции сополимера. ММР бутадиенстирольного сополимера с увеличением объёма реакционной смеси повторяет поведение модельного распределения Шульца–Флори, которое учитывает обрыв цепи в результате взаимодействия с регулятором [5].

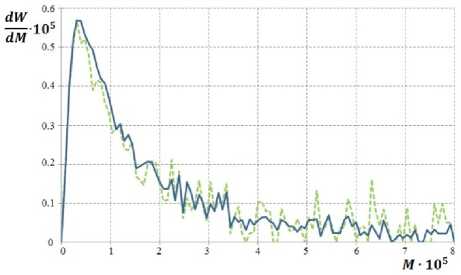
Рисунок 8. Дифференциальная кривая молекулярномассового распределения бутадиен-стирольного сополимера

• Figure 8.    Differential curve of the molecular weight distribution of the butadiene-styrene copolymer

Так как исследуемый процесс производства бутадиен-стирольного каучука является сополимеризационным, то для образующихся макромолекул сополимера помимо отличия по размеру характерно отличие по составу (доле звеньев бутадиена и стирола).

Состав образующегося сополимера характеризует композиционное распределение, которое позволяет определить состав преобладающих в сополимере макромолекул. Для построения композиционного распределения продуктов бинарной сополимеризации необходимо построить соотношение между долей массового содержания первого мономера (бутадиена) в образующемся продукте и числовой долей макромолекул сополимера с учётом их размеров.

На рисунке 9 представлена кривая композиционного распределения продукта сополимеризации бутадиена со стиролом по итогам моделирования 15 и 20 часов ведения процесса. В полученном продукте наблюдается преобладание макромолекул с долей бутадиена в составе в пределах 76–78%.

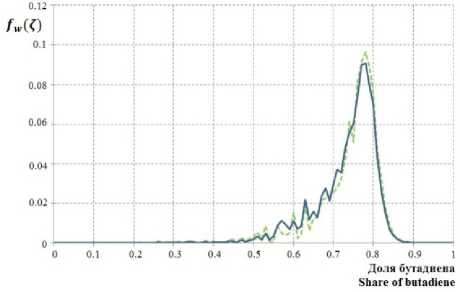
Рисунок 9. Композиционное распределение продукта сополимеризации бутадиена со стиролом, полученного в результате вычислительного эксперимента

• Figure 9.    Compositional distribution of the butadienestyrene copolymerization product received as a result of computing experiment

Для построения распределения макромолекул сополимера по размеру и составу необходимо поделить образовавшиеся макромолекулы сополимера на фракции по массовому содержанию бутадиена и построить соотношение между степенью сополимеризации и числовой долей соответствующих макромолекул сополимера с учётом их размера.

На рисунках 10–12 показаны стационарные состояния, отвечающие различным составам бутадиен-стирольного сополимера по результатам вычислительного эксперимента по моделированию 30 часов ведения процесса.

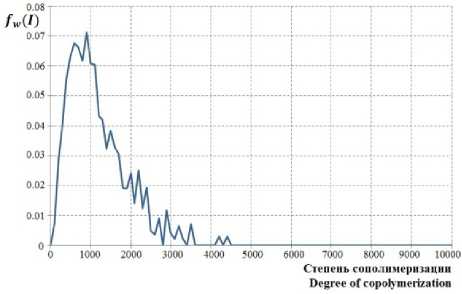
Рисунок 10. Распределение по размеру и составу макромолекул бутадиен-стирольного сополимера (бутадиен – 80%, стирол – 20%)

• Figure 10.    Distribution by the size and structure of the macromolecules of butadiene-styrene copolymer (butadiene – 80%, styrene – 20%)

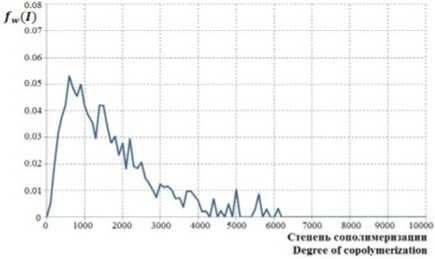
Рисунок 11. Распределение по размеру и составу макромолекул бутадиен-стирольного сополимера (бутадиен – 78%, стирол – 22%)

• Figure 11.    Distribution by the size and structure of the macromolecules of butadiene-styrene copolymer (butadiene – 78%, styrene – 22%)

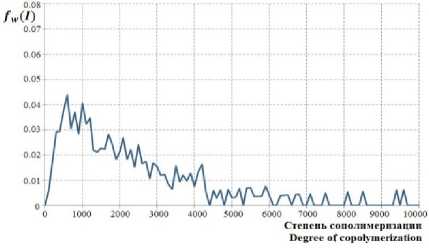
Рисунок 12. Распределение по размеру и составу макромолекул бутадиен-стирольного сополимера (бутадиен – 76%, стирол – 24%)

• Figure 12.    Distribution by the size and structure of the macromolecules of butadiene-styrene copolymer (butadiene – 76%, styrene – 24%)