Моделирование неустановившейся ползучести изгибаемых армированных пластин из нелинейно-наследственных материалов
Автор: Янковский Андрей Петрович
Журнал: Вычислительная механика сплошных сред @journal-icmm
Статья в выпуске: 1 т.11, 2018 года.
Бесплатный доступ
На базе определяющих соотношений нелинейно-наследственной теории ползучести Ю.Н. Работнова с привлечением идеи метода шагов по времени в геометрически линейной постановке сформулирована задача реономного поведения квазистатически изгибаемых перекрестно армированных в своей плоскости пластин. Выведены уравнения и соотношения, позволяющие в дискретные моменты времени с разной степенью точности устанавливать напряженно-деформированное состояние композитных пластин с учетом их ослабленного сопротивления трансверсальным сдвигам. Из построенных уравнений как частные случаи вытекают соотношения классической теории изгиба пластин и традиционных неклассических теорий Рейсснера и Редди. Рассмотрена модельная задача, для которой разработан упрощенный вариант уточненной теории, имеющий примерно такую же сложность реализации, как и теории Рейсснера и Редди. Проведены конкретные расчеты изгибного деформирования армированных кольцевых пластин при кратковременном и длительном нагружении. Продемонстрировано, что для композитных пластин с относительной толщиной порядка 1/10 ни классическая теория, ни теории типа Рейсснера и Редди не гарантируют получения надежных результатов для прогиба даже в рамках грубой 10%-ной погрешности. Точность вычислений по этим теориям ухудшается при увеличении времени длительного нагружения армированной конструкции. На основе соотношений уточненной теории обнаружено, что при изгибе плоско армированных пластин в ряде случаев (например, при использовании низкопрочного связующего и высокомодульных волокон) в окрестности опорных кромок возникают ярко выраженные краевые эффекты, характеризующие резкий сдвиг - «срез» - этих конструкций в поперечном направлении. Показано, что даже при весьма малых уровнях поперечной нагрузки, когда прогибы составляют всего несколько процентов от толщины армированной пластины, при длительном нагружении в связующем материале ее композиции деформации могут достигать 5% и более.
Изгибаемые пластины, армирование, неустановившаяся ползучесть, нелинейная наследственность, неупругое деформирование, теория рейсснера, теория редди, уточненная теория изгиба
Короткий адрес: https://sciup.org/143163493
IDR: 143163493 | УДК: 539.376 | DOI: 10.7242/1999-6691/2018.11.1.8
Текст научной статьи Моделирование неустановившейся ползучести изгибаемых армированных пластин из нелинейно-наследственных материалов
Тонкостенные элементы конструкций типа пластин и оболочек из композиционных материалов (КМ) находят все более широкое применение в инженерной практике. Известно, что все материалы в той или иной степени проявляют реономные свойства [1–5], поэтому актуальной является проблема адекватного математического моделирования армированных пластин, работающих в условиях длительного нагружения. Для успешного решения этой проблемы, с одной стороны, необходимо иметь структурную модель соответствующей композитной среды, материалы компонентов композиции которой обладают заданными реологическими свойствами. С другой стороны, при исследовании изгибного деформирования армированных пластин нужно обоснованно использовать те или иные кинематические гипотезы, позволяющие правильно учесть ослабленное сопротивление таких элементов конструкций поперечным сдвигам.
В работах [6, 7] изучалась реология зернистых КМ, а в [8, 9] моделировалась ползучесть однонаправленно армированных композитных сред (однако такие КМ редко применяются в реальности, разве что в силовых элементах стержневого типа). В [10, 11] построены структурные модели реономного поведения пространственно армированных КМ. Недостаток этих моделей заключается в том, что монолитный в реальности КМ представляется в виде отдельных стержней, ориентированных вдоль направлений армирования, причем указанные армирующие стержни являются несвязанными между собой. В работе [12] предложена структурная модель реономного поведения перекрестно армированных КМ, лишенная данного недостатка.
В отмеченных публикациях механическое поведение материалов компонентов композиции предполагалось линейно- или нелинейно-наследственным, что свойственно, как правило, полимерным материалам [2, 13, 14]. Структурные же теории, описывающие реономное поведение КМ с металлическими компонентами композиции на основе технических теорий ползучести [1, 3–5], на сегодняшний день отсутствуют. Однако, как известно, нелинейно-наследственная теория ползучести Ю.Н. Работнова достаточно хорошо описывает реономное поведение не только полимеров, но и некоторых металлов на первых двух стадиях ползучести при активном нагружении [1–3, 15, 16]. Следовательно, используя эту теорию, можно с единых позиций описать реономное поведение КМ, компоненты которых состоят как из полимеров, так и из металлических материалов.
В работе [17] исследовалась проблема неустановившейся ползучести продольно армированных балок-стенок из нелинейно-наследственных материалов, механическое поведение которых описывается теорией Ю.Н. Работнова. Показано, что при изгибном деформировании таких балок нужно учитывать их ослабленное сопротивление поперечному сдвигу. До последнего времени ползучесть тонкостенных элементов КМ-конструкций в основном изучалась в рамках классической теории изгибного деформирования [18, 19], не описывающей их ослабленного сопротивления поперечным сдвигам. Учет поперечных сдвигов в изгибаемых пластинах и оболочках традиционно осуществляется на базе кинематических гипотез теории Рейсснера– Миндлина [20–23] или теории Редди [24, 25] (которые в русскоязычной литературе называются, соответственно, первым и вторым вариантами теории Тимошенко [26–29]), а также с использованием более точной кинематической гипотезы ломаной линии [30]. В работе [17] показано, что решения задачи неустановившейся ползучести продольно армированной балки-стенки при изгибе, полученные по классической теории и первому варианту теории Тимошенко, недопустимо сильно занижают по модулю прогиб такой конструкции по сравнению с рассчитанным в рамках более точного — второго — варианта теории Тимошенко, учитывающего депланацию поперечных сечений балки. Однако при этом остался открытым вопрос о том, обеспечивает ли второй вариант теории Тимошенко достаточную для инженерных приложений точность вычисления характеристик неустановившейся ползучести армированных балок-стенок или требуется привлечение кинематических моделей изгиба тонкостенных конструкций с более высоким порядком точности [22, 31–33]. В работах [34–36] показано, что при расчете установившейся ползучести или нелинейно-упругого изгибного поведения продольно армированных балок-стенок и волокнистых пластин требуются более точные, чем второй вариант теории Тимошенко, модели изгибного деформирования таких конструкций.
Продольно армированные балки-стенки являются простейшим типом тонкостенных элементов конструкций, в котором реализуется обобщенное плоское напряженное состояние. В тонкостенных конструкциях более сложной геометрии (в частности, в пластинах) при учете их ослабленного сопротивления поперечным сдвигам имеет место объемное напряженное состояние, поэтому в силу нелинейного поведения материалов компонентов композиции (в рамках нелинейно-наследственной теории ползучести Ю.Н. Работнова [1–3, 15, 16]) деформирование армированных пластин в условиях неустановившейся ползучести может обладать специфическими особенностями, которые не проявляются при изгибе композитных балок-стенок.
В работах [37, 38] на основе теории Редди изучалось линейно-вязкоупругое поведение изотропных оболочек, подкрепленных системой ребер. В [28] в рамках классической теории и теории Редди моделировалось линейно-упругое поведение армированных пластин и оболочек при изгибе. Там же построены структурные теории термоупругого поведения композитных сред, исходя из которых с применением принципа Вольтерра [2, 13, 14] получаются определяющие уравнения для плоско армированных тонкостенных элементов конструкций из линейно-вязкоупругих материалов компонентов композиции. Однако никаких решений для композитных пластин и оболочек из вязкоупругих материалов в [28] не приводится.
В связи с этим настоящее исследование посвящено моделированию реономного поведения изгибаемых армированных пластин, механическое поведение материалов компонентов композиции которых описывается соотношениями нелинейно-наследственной теории ползучести Ю.Н. Работнова. При этом ослабленное сопротивление пластин поперечным сдвигам учитывается на базе уточненной теории изгиба, из которой как частные случаи следуют классическая теория, теория Рейсснера и теория Редди.
-
2. Постановка задачи
В ортогональной системе координат x i с началом в точке О рассматривается пластина толщиной 2 h , состоящая из регулярно чередующихся элементарных армированных слоев, параллельных отсчетной плоскости O x1 x 2, совмещенной со срединной плоскостью конструкции (Рис. 1); ось O x 3 ( x 3| < h ) направлена по ее толщине. Структура армирования в поперечном направлении — O x 3, квазиоднородна.
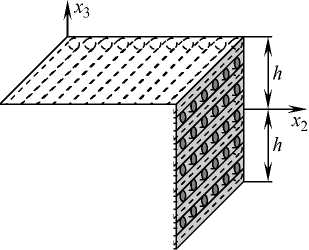
Рис. 1. Элемент армированной композитной пластины
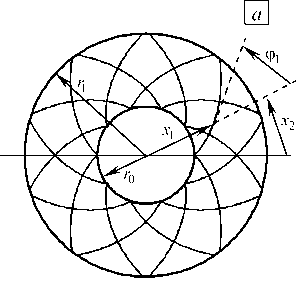
Рис. 2. Структуры армирования кольцевых пластин: ( а ) - спиральная; ( б ) - спирально-окружная
Дй-6-й-(^("^с*)-(')-(')■ (УД ооооооооооо ооооооооооо ^/ ооо-оооооооо x 1 д^^ПОПШЖПП 000-00000000
Предполагаем, что пластина армирована K семействами волокон (на рисунках 1 и 2 а изображены структуры при K = 2, а на рисунке 2 б — при K = 3 ), причем, как и в [17], материалы всех компонентов композиции однородны и изотропны, а их неупругое поведение описывается соотношениями нелинейнонаследственной теории ползучести Ю.Н. Работнова [1-3]:
-
t. ( k )
( k ) ( k ) ( k ) ( к ) т ( к )]_/ k ) B1 ( t Т)t( к )
g 1 (s * , s0 Де у -S у £0 ) = s ij ( t ) + J------ FaT s ij (T) d T ,
0 ( t -t) 1 (1)
t ( k )
g 0 k ) (e(? > , s0 k ) )s0 k ) = O k ) ( t ) +j о k ) ( t ) d T , i , j = 1,3, 0 < k < K , t > 1 0 = 0,
0 ( t -t ) “ 0
где
2 O ( k ) k ) s ( k )
c(k) _ 1 c(k) (k) _ 1 (k) „(k) (k) c(k) ] _ * X * , 0 / „(k) (k) e(
-
S0 = 3 SPP , O0 = 3 °PP , g 1 (S* , S0 ) = -------3 _.....-------, sij = Oij — Sij O0
_( k ) _ Л ( k ) _ „( k ) V + (n< k ) _ „( k ) V + („( k ) _ „( k ) V + 6 k )2 + Q( k )2 + Q( k )2
-
O* = ^— ^(°n ^22 ) + (O22 O33 ) + (O33 O11 ) + 6 (O12 + O23 + O31 ),
-
(k) _ V2 (k) _ (k) v /(k) _ (k) v /(k) _ (k) v (k)2 (k)2(
£ * 3 ^( ^ 11 ^ 22 ) + ( ^ 22 £ 33 ) + ( ^ 33 ^ 11 ) + 6 ( ^ 12 + ^ 23 + ^ 31 ) , i , j 1, 3, 0 < k < K .
В (1), (2) обозначено: о(к), s(jk) — компоненты тензоров напряжений и деформаций в k-й фазе композиции (значение индекса k = 0 определяет характеристики связующего, а значения k > 1 — характеристики k-го семейства арматуры); g(k) (s*k), s0k)) — известная из эксперимента функция, которая при умножении на 3/2 является коэффициентом пропорциональности между интенсивностями напряжений о*k) и деформаций s*k) в k-м компоненте композиции; g0k) (s*k), s0k)) — известная из эксперимента зависимость от аргументов s*k), s0k) утроенного объемного модуля материала k-й фазы композиции; а(k) — показатели слабой сингулярности ядер ползучести того же материала; B;(k) (t)
—
регулярные составляющие
(возможно, постоянные) ядер ползучести ( l = 0,1); 1 0 — начальный момент времени t ; S j — символ Кронекера; по повторяющимся греческим индексам производится суммирование от 1 до 3. Функции g 0 k ) , g 1 k ) (или o (, k ) ) рассчитываются по диаграммам мгновенного деформирования материала k -го компонента композиции, а их зависимость от двух аргументов s ( k ) и s 0 k ) позволяет учитывать разносопротивляемость материала, которая часто наблюдается в экспериментах на ползучесть [1, 3, 14].
Как и в работах [12, 17, 39], для описания реономного поведения композитной среды используем идею метода шагов по времени, причем считаем, что в предшествующие дискретные моменты времени tl ( l = 0,1,2,..., n ) решение исследуемой задачи уже известно, поэтому на основе структурных формул из [12] и результатов дискретизации по времени [17, 39] можем построить определяющие соотношения для КМ в текущий момент времени tn + 1.
Предполагая, что левые части равенств (1) удовлетворяют достаточным условиям сходимости метода последовательных приближений (см. стр. 199 в [14]), аналогичного методу переменных параметров упругости, линеаризуем соотношения (1) при t = tn + 1. Повторяя рассуждения из [39], исходя из (1) получим линеаризованные определяющие уравнения для всех компонентов композиции, которые на каждой итерации в момент времени tn + 1 формально совпадают с соотношениями для линейно-упругой среды с заданным начальным напряженным состоянием. Согласно [12], эти соотношения при t = tn + 1 на текущей итерации дают линейные определяющие уравнения для волокнистой композиции:
Су (r, t ) = aij а₽( r, t )£ар( r, t) + Py (r, t) , r = { x1, x 2, x 3} , t = tn+1, i = 1, 3, где cij, £у — осредненные напряжения и деформации в композиции; aijls — эффективные жесткости композиции на текущей итерации метода последовательных приближений, которые определяются через механические характеристики и деформированное состояние компонентов композиции (см. (1), (2)) и параметры армирования: плотности юk и углы армирования фk (1 < k < K), отсчитываемые от направления Ox1 (Рис. 2а); pij — компоненты «начальных» напряжений в композиции, которые обуславливаются предысторией нагружения представительного элемента композиции, зависят от параметров армирования и вычисляются, как и aijls , по структурным формулам, приведенным в [12].
Так как материалы фаз композиции изотропны, а армирование пластины осуществляется параллельно плоскости O x 1 x 2 (Рис. 1), не все эффективные жесткости в (3), согласно [12, 36], отличны от нуля, а именно:
aiil 3 a 12 l 3 a 3312 a 1323 0, l 1, 2 ( a ijms a msij a jims a jism a ijsm , i , j , m , s 1, 3) . (4)
В силу того что толщина армированной пластины много меньше ее характерного размера в плане, напряжение c 33 в (3) с приемлемой точностью будем считать определенным за счет его аппроксимации по координате x 3 на основе силовых граничных условий, заданных на лицевых поверхностях пластины. В первом приближении примем линейную по x 3 аппроксимацию с33 [29]. В работе [36] показано (см. там формулу (1.20)), как в случае квазистатического нагружения пластины с помощью метода дополнительных граничных условий и метода коллокаций можно существенно уточнить аппроксимацию напряжения с 33 по переменной x 3 при реализации метода последовательных приближений. Именно этот метод и применяется в данной работе. Заметим, что традиционно в тонкостенных элементах конструкций напряжением с 33 вообще пренебрегают при преобразовании определяющих соотношений (3), то есть исходя из силовой гипотезы используют аппроксимацию c 33 ( r , t ) ® 0 [17-28, 30, 34, 35, 37, 38]. Предполагая, что аппроксимация с .. по x 3 известна, из равенств (3), принимая i = j = 3 и учитывая (4), исключим деформацию £ 33. Тогда в момент времени tn + 1 на текущей итерации окончательно получим следующие определяющие соотношения для КМ рассматриваемой пластины:
С у ( r , t ) = j ( r , t ) £ ij ( r , t ) + C 0 ( r , t ) , i , j = 1,2; cn ( r , t ) = 2 ani3 ( r , t ) б , -3 ( r , t ) + P i 3 ( r , t ) , i = 1, 2,
где b..
iijj
— a iijj a 3333 a i. 33 a jj 33 , b ii 12 b ii 21 — a n 12 , CH — p H + a 3333 au 33 ( c 33
£ 33 = a 3333 ( c 33 — p 33 — a 33 ll £ ll ) ;
P 33 ) , C 02 — P 12 , i , j = 1, 2, (7)
по повторяющимся прописным латинским индексам проводится суммирование от 1 до 2. Согласно (7), величины bjls , ai3i3 , c 0 , pi3 в (5), (6) уже найдены в результате решения исследуемой задачи на предыдущей итерации метода последовательных приближений.
Равенства (5), (6) аналогичны определяющим уравнениям из [36], где под ст “ понимались мгновенные температурные напряжения. В настоящем исследовании величины ст “ и pi3 в (5), (6) зависят от предыстории нагружения представительного элемента композиции пластины, но в общем случае к ним могут быть отнесены и температурные напряжения, если учитывается тепловое воздействие на конструкцию. Далее ради экономии места в силу указанной аналогии будем использовать результаты работы [36].
Теории, учитывающие ослабленное сопротивление рассматриваемой армированной пластины (Рис. 1) поперечным сдвигам, традиционно строятся на базе тех же гипотез, что и классическая теория, но только при задании ненулевых деформаций поперечных сдвигов s i 3. Согласно теории Рейсснера, эти деформации принимаются постоянными в поперечном направлении O x 3 [20, 22, 23, 29], в рамках же теории Редди они аппроксимируются полиномами второго порядка по переменной x 3 [24-28]. В последнем случае удается удовлетворить статические граничные условия на лицевых поверхностях конструкции по касательным напряжениям ст i 3 ( i = 1,2). В соответствии с этой идеей для уточнения теории Редди представим деформации s i 3 в виде полиномов ( M + 2)-го порядка по переменной x 3. Тогда в рамках геометрически линейной постановки задачи в декартовой прямоугольной системе координат получим следующие выражения для перемещений u i и осредненных деформаций композиции sij [36]:
si3 (r, t ) = П x^+h s (^ ( x t ) — x^^h s /V ( x t ) + h-^x3- ]Tx 3m £(m) ( X, t ) , x = { xp x 2 } , _ 2 h 2 h J h m=o i = 1,2; (8)
s-j (r, t ) = (Vj +8Х ) /2 - x 38i8ju 30 + S fm ( x3 X^j? +8JS Й) ) + f(+) ( x 3 ^j +8^ (+1 )- m
- f H ( x 3 ) ( 8,s (j - ) +d j S( 3 -)) , x 6 G , | x 3| < h , t > t 0 , i , j = 1,2; (9)
u 3 ( r , t ) = U 0 ( x , t ) , x 6 G , |x 3] < h , t > 1 0 ;
U i ( r , t ) = u i ( X , t ) - x 3 d i u 0 ( x , t ) + 2 ^ f m ( x 3 ) s(3 m ) ( x , t ) + 2 f (+) ( x 3 ) s(3+) ( x , t ) - 2 f (-) ( x 3 ) s(3-) ( x , t ) , i = 1, 2 . (11)
m
В выражениях (8)-(11) приняты обозначения:
fm ( x 3 ) = h 2 xm +1 ( h 2 ( m + 1 ) 1 -p x 3 2 ( m + 3 ) 1 ) , f (±) ( x 3 ) = 0,25 ц h' x 3 ( x 3 ± 2 h ) , |x 3| < h ; (12)
u i 0 — перемещения точек срединной поверхности пластины в направлениях O x i ( i = 1,3); s j ±) — деформации поперечных сдвигов на верхней и нижней ( x 3 = ± h ) лицевых поверхностях конструкции; д i — оператор дифференцирования по переменной xj ( j = 1, 2); G — область, занимаемая пластиной в плане; п — параметр переключения. По индексу m производится суммирование от 0 до M , как указано в (8). Равенство (10) соответствует традиционной для тонкостенных элементов конструкций кинематической гипотезе, согласно которой изменяемостью прогиба u 3 в направлении O x 3 пренебрегают [17-28]. В качестве неизвестных выступают кинематические переменные u 0 , u 3 0 , s (±’ , s ( m ) ( i = 1,2, 0 < m < M ), зависящие от времени t и только двух пространственных координат x 1 и x 2.
В дальнейшем из (8)-(11) получаются следующие уравнения: при п = 0 и s im ) ( x , t ) = 0 (0 < m < M , i = 1, 2) уравнения, отвечающие кинематическим гипотезам классической теории [22, 28]; при п = 1 и M = 0 и учете (12) — соотношения, основанные на гипотезах теории Редди [24-28]; при п = 1 и M > 1 — уточнения теории Редди [24, 31-34, 36]; при п = 0 и M = 0 и (12) — равенства теории Рейсснера [20-23].
Подставляя (8), (9) в (5), (6) и учитывая (7) и (12), выразим осредненные напряжения в композиции ст (/ через кинематические переменные u 0 , s ( m ) и s (±) ( i = 1, 2 , j = 1, 3, 0 < m < M ). Используя получившиеся при этом выражения, определим все необходимые внутренние силовые факторы, возникающие в пластине (см. [36]):
-
( l ) l ) »0 R( l ) я0 Г’( l ■ m)й (mm ) 7Э( l ) p(+) T7( l ) p(-) P( l )
M ij ( x , t ) = A jJJ д I u J B UU д I д J u 3 + ^ C ijIJ д I s J 3 + D ijIJ д I s J 3 E ijIJ д I s J 3 + P j ( x , t ) ,
m
M ^ ( x , t ) = ^ G^ m ) s i 3 m ) + Ft 31 ) s (3+) - H il s i -) + Pt 31) ( x , t ) , (13)
m
-
i , j = 1,2, l = 0,1,..., ( 2/3 ) M + 1, x 6 G , t > 1 0 ,
где
hhh
M k ( x , t ) = J c ik ( r , t ) x ‘ dx 3 , P ‘ ) ( x , t ) = J ст 0 ( r t ) x ‘^ dx 3 , P i 3 ‘ ’ ( x , t ) = J P a ( r , t ) xidx 3 ,
- h - h - h
h
j ( x , t ) = J b ins ( r , t ) x 3 dx 3 , j ( x , t ) = j ” ( x , t ) ,
- h
h
j ’ ( x , t ) = 2 J b ijns ( r , t ) x ‘i f m ( x 3 ) dx 3 ,
- h
hh
D ils ( x , t ) = 2 J b ijns ( r , t ) x ‘i f (+) ( x 3 ) d x 3 , j ( x , t ) = 2 J b ijns ( r , t ) x if (-) ( x 3 ) d x 3 ,
- h - h
G^' 3 ) ( x , t ) = 2 J ai3 i 3 ( r , t ) x 3+ m dx 3, F i 3 ‘ ) ( x , t ) = П J ai3 i 3 ( r , t ) x 3 ( x 3 + h ) dx 3,
- h h - h
h
H ( 3 l ) ( x , t ) = П J a ,3,3 ( r , t ) x ‘ ( x 3 - h ) dx 3, h^
i , j , n , s = 1,2, k = 1,3, 0 < l < ( 2/3 ) M + 1, 0 < m < M .
Здесь и далее предполагаем, что число M кратно трем (см. (8)). Согласно первым равенствам (14), M j 0) = F j , M j1 = M j — мембранные силы и изгибающие и крутящие моменты в конструкции, M i ( 3 0) = F i 3 — поперечные силы, / /"’, p 30) , р /1’ — « начальные» мембранные и поперечные усилия, а также изгибающие и крутящие моменты; остальные внутренние силовые факторы — механические моменты высших порядков. Начальные силовые факторы P j‘ ) , р 3 ‘ ) ( i , j = 1, 2) на данной итерации метода последовательных приближений в текущий момент времени являются известными величинами.
Задача рассматривается в квазистатической постановке, поэтому силовые факторы M ( ) , введенные в (14), должны удовлетворять уравнениям равновесия [36]:
d J M ^J ) - lM ^-1) = - X (‘ ) - hl [ст (+) - ( - 1 ) ‘ ст i - ) ] , d J M Jl) = - X 3 ( l ) + l J x 3 - 1 ст 33 dx 3 - h l [ст 3+) - ( - 1 ) ‘ ст 3 - ) ] , - h
0 < l < ( 2/3 ) M + 1, i = 1,2;
0 < l < ( 2/3 ) M , x e G , t > 1 0,
где
X (‘ ) ( x , t ) = J X ( r , t ) x 3 dx 3 , ст i 3±) ( x , t ) = сти ( x , ± h , t ) , i = 1,3; (16)
- h
Xt — компоненты объемной нагрузки, действующей на КМ; напряжения ст (±) определяются из силовых граничных условий на лицевых поверхностях конструкции x 3 = ± h . Напряжение ст 33 ( r , t ) , как уже отмечалось при выводе соотношений (5) и (7), предполагается известным за счет аппроксимации его по заданным напряжениям ст (±) (подробнее см. формулу (1.20) в [36]), поэтому интеграл в последнем равенстве (15) перенесен вправо.
К системе уравнений (15) следует добавить четыре силовых граничных условия на лицевых поверхностях конструкции (см. (6) и (8)):
2 ai3i 3(x , ± h , t )I h 2 П x 3 У x m s ( 3m ) +n x ^+ h б * / ) -n x^- h e ( 3 - ) 1313 ( ) l h 2 Zm‘ 31 3 2 h i 3 2 h i 3
+ P i 3 ( x , ± h , t ) = ст (±) ( x , t ) ,
i = 1, 2, (17)
где pi 3, правые части и коэффициенты ai3i3 известны на текущей итерации, поэтому при п = 1 получаем
б (±) ( x , t ) = ( ст (±) ( x , t ) - p B ( x , ± h , t ) )/( 2 a i3i3 ( x , ± h , t ) ) , x e G , t > 1 0 , i = 1,2. (18)
Таким образом, при использовании теории Редди или ее уточнений ( п = 1, M > 0) из уравнений (17) на текущей итерации можно однозначно определить функции б i ±) ( x , t ) , i = 1, 2 (см. (18)), то есть два первых слагаемых в разложении (8). В рамках же теории Рейсснера ( п = 0, M = 0) или классической теории ( п = 0 , б im ) = 0) силовые граничные условия (17) в общем случае удовлетворить нельзя.
Для однозначного интегрирования исследуемой задачи на кромках пластины должны быть известны соответствующие граничные условия. Если на одной части торцевой поверхности конструкции (обозначим её как G a ) заданы силовые граничные условия, то для введенных силовых факторов (14) они имеют вид [36]:
n^M J " = M n 1К " ( x , t ) , ( - 1 ) I n з- , n J M J " = М П Т" ( x , t ) , 0 < l < ( 2/3 ) M + 1,
П/М# = МП 3) (x, t), 0 < l <( 2/3) M, n = cos y, n 2 = cos y, x eF„, t > t0, где hh мПn" (x, t) = J ann (r, t)x3dx3, мПТ) (x, t) = J anТ (r, t)x3dx3,
- h h - h (20)
М П 3" ( x , t ) = J ^ n 3 ( r t ) x 3 dx 3 , x еГ a , r е G a , t > t 0 ;
-
- h
a nn , a n Т , a n 3 — нормальная, касательная (в плоскости x 3 = const) и поперечная (в направлении x 3) внешние поверхностные нагрузки на G a ; Г a — проекция части торцевой поверхности G a на отсчетную плоскость x 3 = 0 ( Г a — часть контура Г, ограничивающего область G , занимаемую пластиной в плане); Y — угол между внешней нормалью и контуром Г; M nn , М П /, M nl 3 " — силовые факторы на контуре Г a . Согласно (20), являются известными М П 0" ^ Fnn , M n (0) ^ Fn Т — нормальная и касательная к Г a мембранные силы, М П 0) ^ Fn 3 — поперечная сила, M nn = Mnn , Мр = Mn Т — изгибающий и крутящий моменты на Г a , механические моменты высших порядков, входящие в правые части равенств (19) .
Если на части торцевой поверхности (обозначим ее G u ) заданы кинематические граничные условия, то, используя выражения (10) и (11), при учете (12) получим [36]:
и 3 ( x , t ) = и 30 ( x , t ) , x d u , t > t 0 ; (21)
h +1 ( l + 1 ) -1 ( 1 + ( - 1 ) l ) u " - h +2 ( l + 2 ) ' ( 1 - ( - 1 ) l )дц( 3 0 + 2 Е h m + 1 +2 ( 1 - ( - 1 ) l + m )( ( m + 1 ) -1 ( l + m + 2 ) -1 - m
-П (m + 3)-1 (l + m + 4) ')e(m" + nhl+2 [0.5(l + 3) ' (1 + (-1)l) + (l + 2)-1 (1 -(-1)l)]e3 ■ -
-
-П h1 + 2 [ 0.5 ( l + 3 )- 1 ( 1 + ( - 1 ) l ) - ( l + 2 )- 1 ( 1 - ( - 1 ) l ) ]e 3 d = u < 0" ( x , t ) , x еГ „ , t > t 0 , i = 1,2, 0 < l < M + 1, (22) где
h
-
u , (0" ( x , t ) ^ J ui0 ( r , t ) x l dx 3, x еГ u , r е G u , t > t 0, i = 1,2, 0 < l < M + 1; (23)
- h
Г u — проекция части торцевой поверхности G u на отсчетную плоскость ( Г = Г а U Г u ); и 30 — заданный на контуре Г и прогиб; и 0 — известные на торцевой поверхности G u перемещения в тангенциальных направлениях x i . Согласно (23), равенства (22) следуют из исходных кинематических граничных условий u i ( r , t ) = ui0 ( r , t ) ( r е G u , t > 1 0, i = 1, 2 ) в результате применения метода взвешенных невязок и при учете (11) и (12); в качестве весовых функций использованы однородные полиномы x 3 .
Подставим выражения (13) в равенства (15), примем во внимание (16) и тогда получим уравнения равновесия в разрешающем виде:
d L ( A LIj d , u J - B Lj д I д J U 30 + Е C Lm ) д I e Jm ) - 1 Е G 3 "'• m ) e (3 m ) = - X ( l ) - h l [a (+) - ( - 1 ) l a (-) ] - d l ( D « d , e J - mm
-
- E^ д I eJ- + PLl)) +1 (Fi 3l-1) e- H^1 e+ p 3l-1)), 0 < l <( 2/3) M +1, i = 1,2,(24)
h
У d, G < l3m )e< m )) = - X l ) + 1 x* -1 a33 dx 3 - h l [a (+) - - 1 ) l a (-) ] - d, F ( l"ep: - H e (,-’ + P/l )) , 0 < l < 2/3) M .
J \ J 3 J 3 / 3 I 3 33 3 33 у ) 33 J \ J 3 J 3 J 3 J 3 J 3 /,
-
m-
Подстановка выражений (13) в соотношения (19) приводит к статическим граничным условиям, выраженным через кинематические переменные:
( 1 ’ 8u0-R( 1 ’ 0 С( 1 - m ’йг( mА-М(1 ’ ( 1 ’ Rf^-F- ’ г(-) Р( 1 ’)
n N n L ( A NUJ ° I u J B NIIJ ° I ° J u 3 + A C NIIJ ° I S J 3 ) M nn n N n I ( D NIIJ ° I S J 3 E NIJJ ° I S J 3 + P NI ) , m
(-1) N n 3-nUi (ANIIJ 3 IuJ - BNIIJ dI djU 0 + £ CNIJ dI J ) = m (25)
= M U T’ - ( - 1 ) N n 3- nUi ( D N l IJ d I s J +’ - E NNIIJ d I s J -’ + P NI ') , 0 < 1 < ( 2/3 ) M + 1,
Ул G( 1 , m ’s( m ’ =M( 1’(l^ 1 )e( + ) -Я( 1 )e(-) +P( 1 ’^ 12/3)4/ хеГ
/ . nJ G J 3 s J 3 M n 3 n J ( FJ 3 s J 3 H J 3 s J 3 + P J 3 ) , 0 < 1 — ( 2/3 ) M , x ^ ст , t — t 0
m
В уравнениях (24) и (25) в правые части перенесены все известные на текущей итерации слагаемые, в частности, содержащие функции s^ , которые уже определены из равенств (18) при п = 1 . В случае П = 0 , согласно (14), коэффициенты при s N±’ ( i = 1, 2 ) и их производных тождественно равны нулю, и поэтому в (24), (25) соответствующие члены отсутствуют. Таким образом, решение исследуемой задачи в момент времени t n + 1 на каждой итерации метода последовательных приближений сводится к реализации уравнений (18), (24) при статических (25) и кинематических (21), (22) граничных условиях.
На основании формул перехода от декартовой прямоугольной системы координат к цилиндрической [40] и приведенных выше соотношений можно получить систему разрешающих уравнений и соответствующие ей граничные условия в полярной системе координат.
-
3. Модельная задача
Для демонстрации необходимости уточнения традиционных теорий изгиба (классической, Рейсснера и Редди) при реономном поведении тонкостенных волокнистых элементов изделий рассмотрим осесимметричный изгиб кольцевой пластины толщиной 2 h , ограниченной кромками с радиусами r0 и r (Рис. 2). Положения точек пластины зададим в цилиндрических координатах x i , где х , — полярный радиус, х 2 — полярный угол (0 < х 2 < 2 п ), х 3 — осевая координата, которая перпендикулярна плоскости рисунка 2. Закрепление и нагружение конструкции не зависят от х 2, внешние силы в окружном направлении отсутствуют. Пластина усилена осесимметрично: 1) двумя семействами волокон ( K = 2) с одинаковыми плотностями армирования (ц ( х 1 ) = ® 2 ( х , ) ), уложенных по радиально-симметричным направлениям ( ф 1 ( х , ) = -ф 2 ( х , ) ) (спиральное армирование, Рис. 2 а ); 2) тремя семействами волокон ( K = 3 ), два из которых уложены радиально-симметрично ( ф , ( х 1 ) = -ф 2 ( х , ) ) с одинаковыми интенсивностями армирования ( ® , ( х , ) = « 2 ( х , ) ), а третье семейство уложено в окружном направлении ( ф 3 ( х , ) = п /2) с плотностью ю 3 ( х , ) ( r0 < х , < г ) (спирально-окружное армирование, (Рис. 2 б )). В обоих случаях волокна разных спиральных семейств изготовлены из одного и того же материала.
При таком нагружении и структуре армирования, согласно [12, 36], имеют место равенства (см. (5), (6)):
b ii,2 = b 12 ii = b ii2, = b 2,ii = 0 ° 02 = P 23 = 0 i = I2. (26)
На основании соотношений (5)-(7), (26), а также особенностей закрепления и нагружения рассматриваемой пластины решение задачи ее изгибного деформирования не зависит от полярного угла х 2 , причем в реализующемся осесимметричном процессе обнуляются следующие компоненты:
и 2 ( х , , х 3 , t ) = 0, е 12 ( х , , х 3 , t ) = S 23 ( х , , х 3 , t ) = 0, о 12 ( х , , х 3 , t ) = ^ 23 ( х , , х 3 , t ) = 0. (27)
Исследуем наиболее часто встречающийся тип изгибного нагружения пластины, когда на лицевых поверхностях х 3 = ± h касательные силы отсутствуют ( ст i /’ ^ 0 ), поэтому при п = 1 (теория Редди или ее уточнения) из (18), согласно [12], имеем: s (±) ^ 0, i = 1,2. Функции s 13 ( х 1, х 3, t ) , s t1 ( х 1, х 3, t ) и U j ( х 1, х 3, t ) при этом определяются соотношениями (8), (9), (11), а деформация s 22, при учете (11), (12), выражается так [40]:
S 22 ( х , , х 3 , t ) = х /1 u , = х /1 ( u ,0 - х 3 8 ] u 30 + 2 ^ fm ( х 3 ) s ( m ’ ) , |х 3I < h , r , < х , < r , t — 1 0 . (28)
m
Для простоты проанализируем частный случай закрепления кольцевой пластины: одна из кромок (например, внутренняя) жестко заделана, то есть при х , = r 0 выполняются соотношения (21), (22),
Для простоты проанализируем частный случай закрепления кольцевой пластины: одна из кромок (например, внутренняя) жестко заделана, то есть при x 1 = r0 выполняются соотношения (21), (22), при этом ui0 = 0 ( i = 1,3); на другой кромке (например, внешней) заданы силовые граничные условия (19) и учитываются формулы (20) ( x 1 = r 1 , у = 0 и ст n т = 0). При этом можно построить упрощенный вариант уточенной теории, сложность реализации которого сопоставима со сложностью при применении теорий Редди и Рейсснера. Для внутренних силовых факторов (см. (14)) при этом получаем систему уравнений равновесия (см. формулы (2.4) и (2.5) в [36]):
di F11 + (Fu - F22)/xi = - X(Xi, t), diM11 +(M11 - M 22)/xi = F13 - X(1) (xn t), гй < xi < r, t — t0; (29) h d1 (x1 M 1(3)) = -x1 X3(l) (x1, t) + lx1 j x3-1ст33dx3 -hlx1 ^ст;,' (x1, t)-(-1)‘ ст3-) (x1, t)], 0 < I < M, r0 < x1 < ri, t — t0. (30) - h
В силу того, что на внешней кромке выполняются силовые граничные условия (19), где x 1 = r 1 , у = 0 и ст n т = 0, по аналогии с уравнениями (29) и (30) в текущий момент времени имеем:
F11 (ri, t) = Fnn (t), M11 (ri, t) = Mnn (t), t — 10;(31)
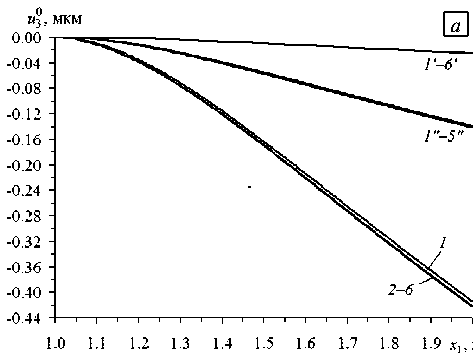
Mi(3)(r, t) =Mn3)(t), 0 Используя равенства (5), (6), (8), (9) и (28), при учете (14), (26) и (27) найдем все внутренние силовые факторы, входящие в соотношения (29)–(32): F A- 4 (0)Я „0 _ Л(1) Л2„0 . (0. m )я p( m) -I- vA „0 _ Л0) Я „0 . V C (0-m) p( m) ) 4. P (0) ( v Л Fii (xi, t) Aii 11d1 ui Aiiii^i u 3 + A Ciiii d1£13 + X1 (Ai 22 ui Ai22di u 3 + ^ Cii22 £13 ) + Pii (X1, mm W A— 4(1)Я и0 — /1(2)Я2»0 V Г’(1,m A P(m) 4- v-1 ( /f(1)11° — Л(2)Я 11° 4- V Г^1, m) P(m ) \ P(i) ( v i — 1 Э Mil (X1, t) Aiiii^i ui Aii11di u 3 + ^ Ciiii diei3 + X1 (Aii22 ui Aii22d1 u 3 +^ Cii22 £13 ) + Pi (X1, t), i 1, 2, mm (l) (l,m) (m) (l) M13 (xi, t ) / ^ VJ|3 (xi, t )&i3 (xi, t) + P 13 (xi, t), 0 < l< M , r) < xi < ri, t — t 0 (34) m Как и в разделе 2, предполагаем, что напряжение ст33(x1, x3, t) известно за счет соответствующей аппроксимации (см., например, формулу (1.20) в [36]), поэтому при каждом l правая часть в (30) определена, и это равенство представляет собой простейшее обыкновенное дифференциальное уравнение первого порядка относительно функции M1(3l)(время t играет роль параметра), для однозначного интегрирования которого следует использовать граничное условие (32). Если краевая задача (30) и (32) при каждом l решена (в текущий момент времени t = tn+1 на данной итерации метода последовательных приближений установлены M 1(3) (x1, t)), то равенства (34) при известных, согласно (14), функциях P113l) (x1, t) в каждой точке r0< x1 < r1 образуют замкнутую систему линейных алгебраических уравнений относительно искомых параметров s(m) (x1, t). В результате ее решения при t = tn+1 можно найти значения этих функций, входящих в разложение (8) при i = 1. После этого в выражениях (33) неопределенными остаются только функции U10(x1, t) и и30(x1, t). Подстановка соотношений (33) в (29) приводит к системе разрешающих уравнений относительно этих функций, которая, при соответствующих переобозначениях зависимых переменных и коэффициентов, полностью совпадает с системой (2.10) в [36]. Для однозначного интегрирования этой системы необходимы статические (31) (при учете (33)) и кинематические (21), (22) (при и30= 0, U0) = 0, x1 = r0, i = 1 и l = 0,1) граничные условия. Методы численного решения получающейся при этом двухточечной граничной задачи подробно рассмотрены в [36], поэтому здесь не приводятся. 4. Обсуждение результатов расчетов На конкретном примере кольцевой пластины толщиной 2h = 10 см, ограниченной кромками с радиусами r0= 1 м, r1 = 2 м, проанализируем особенности ее изгибного реономного деформирования. Нелинейно-наследственное поведение матрицы — алюминиевого сплава Д16Т, описывается соотношениями (1) и (2) при следующих механических характеристиках [3]: а (0)(Р(0) о (0)^ - 2 j(0) (р(0) Г 0‘ o-(0)fp(0) р(0)^- E nit R (0) (А - А(0) h r/(0)^-mnQf g 1 Iе. , е0 ) = ТAi (S, ) , g0 (8. , £0 ) = ----— . = const, Bi (t) = bi (1 -ai ) = const, 3 1 - 2V B00)(t) = 0, E(0) = 64 ГПа, v(0) = 0,31, A = 30,55 ГПа, b^ = 0,119 ч1—<’,(35) a(0)= 0,635, m0= 0,87. Пластина может быть осесимметрично армирована двумя (K = 2, Рис. 2а) или тремя (K = 3 , Рис. 2б) семействами углеродных (С) волокон марки Торнел-75 с механическими характеристиками [41]: (k)( B0k)(t) = Bk)(t) = о, g0k) (е<k), s0k) )= (k) = const, g(k) (s<k), s0k) ) = —ky = const, (36) 1 — 2V 1+ V E(k) = 525 ГПа, v(k) = 0,25, 1 < k< K. Здесь E(k), v(k) (0 < k< K ) — модуль Юнга и коэффициент Пуассона материала k-го компонента композиции. Согласно соотношениям (35) и (36), в рассматриваемых условиях углеродные волокна не ползут и ведут себя линейно-упруго [41], для сплава Д16Т связь между шаровыми тензорами напряжений и деформаций также является линейно-упругой [14]. На внутренней кромке пластина жестко закреплена (см. (21)-(23) при l = 0,1 и u30= ui0^ 0, х1 = r0, i = 1, 2), а внешняя кромка свободна от нагружения: Fnn = 0 , Mnn = 0 , МП3) = 0, 0 < l< M (см. (31) и (32)). Конструкция равномерно нагружена только поперечной распределенной нагрузкой ^3+) (^3—) ^ 0, □ i±) ^ 0 , Xj = 0, i = 1, 2 , j = 1, 3; см. (16)), которая прикладывается в соответствии с функцией класса Хевисайда: (+), х (0 при t< 0, о„) t = — qх, „ q = const>0
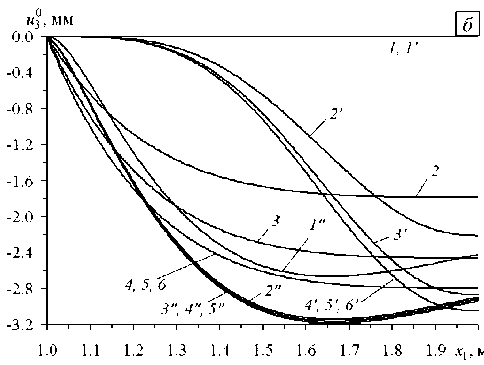
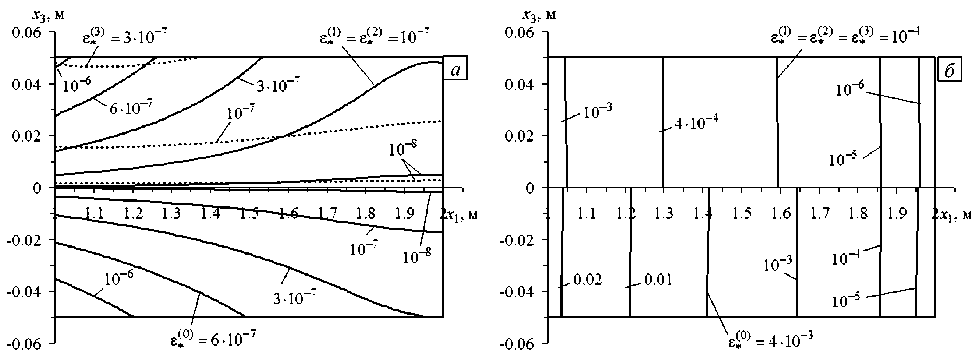
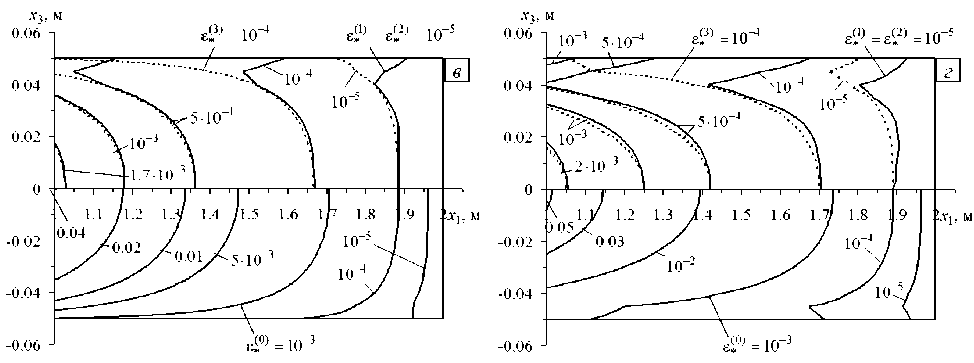
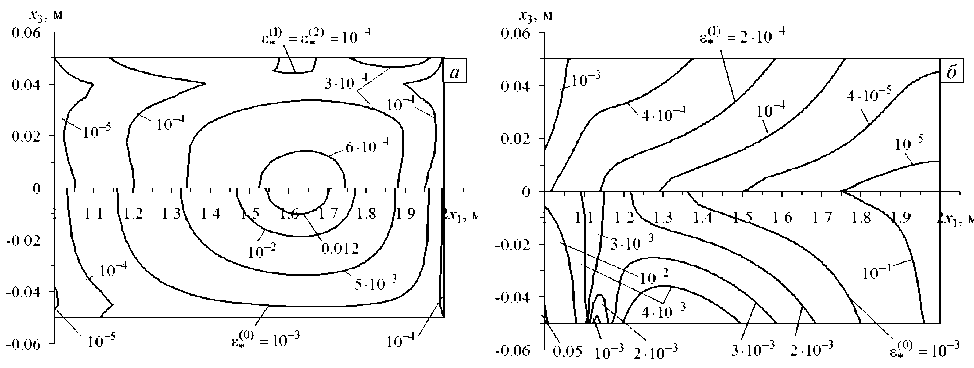
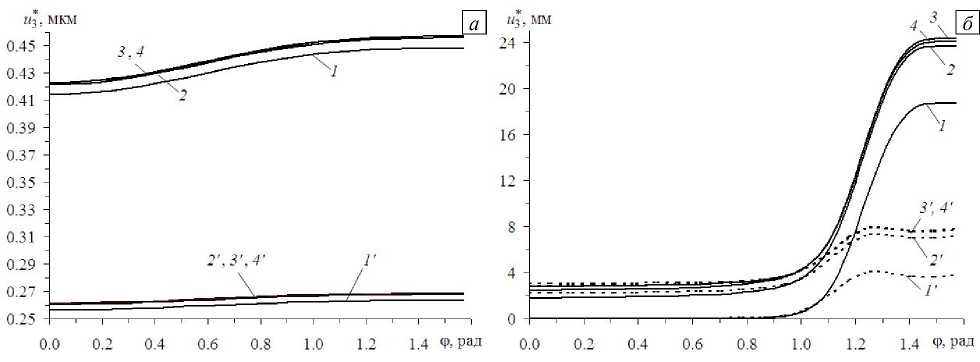
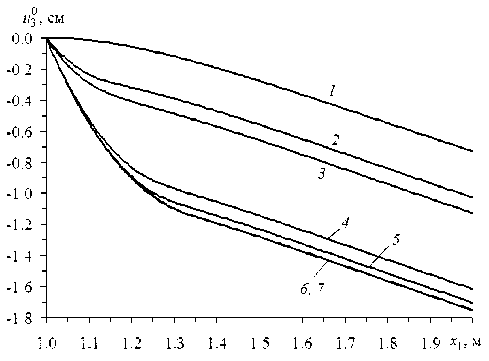
33 v ’ 4 [1 при t > 0, 4 Согласно модельной задаче, пластина осесимметрично армирована: 1) двумя семействами волокон Торнел-75 (K = 2) по логарифмическим спиралям (Рис. 2а), то есть ю (х1 ) = ю2 (х), Ф1 (х ) = —Ф2 (х1 ) = ф = const, г0 < х < г; 2) тремя семействами углеродных волокон (K = 3 ), причем первые два семейства (k = 1, 2) по-прежнему ориентированы радиально-симметрично по логарифмическим спиралям, для них выполняются соотношения (38), а третье семейство уложено в окружном направлении (ф3= л/2) с плотностью армирования ю3(х1) (Рис. 2б). Так как углеродные волокна имеют постоянные поперечные сечения [41], плотности армирования юk в осесимметричном случае при укладке волокон по логарифмическим спиралям под любыми углами φ изменяются по закону [28, 36]: Юk (Х1 ) = ^^, Г0< Х1 < Г(Ю0 k = Юk (Г0 ), k = 1,2 Ю01 =ю02), (39) x1 где ю0k — плотность армирования волокнами k-го семейства, заданная на внутренней кромке х1 = r0. Из равенств (39) вытекает, что при любых углах армирования φ (см. соотношения (38)) общий расход волокон спиральных семейств в конструкциях фиксированных размеров при одинаковых ю0k (k = 1, 2) будет один и тот же. Далее для спирально армированных пластин (K = 2; Рис. 2а) принимаем ю01=ю02= 0,35. Суммарная плотность армирования при этом на внутренних кромках (ю01+ю02= 0,7) достигнет предельно допустимого значения, которое на практике равно примерно 0,7. Согласно выражению (39), при спиральной укладке волокон (Рис. 2а) суммарная плотность армирования ю(х1) = ю1 (х1) + ю2 (х1) = 2ю1 (х1) монотонно убывает от внутренней кромки пластины х1 = r0 к внешней х1 = r1. Так как для окружного семейства волокон (ф3 =л/2 ; Рис. 2б) плотность армирования ю3 (х1) может быть произвольной функцией полярного радиуса х1 [28], выберем ю3 (х1) таким, чтобы при спирально-окружной укладке волокон суммарная плотность армирования ю(х1 ) = ю1 (х1 ) + ю2 (х1 ) + ю3 (х1 ) = 2ю1 (х1 ) + ю3 (х1) была величиной постоянной, причем потребуем выполнения равенства ю(х1 ) = 2ю01 = const. Следовательно, интенсивность армирования окружным семейством волокон при учете (39) определяется так: Юз (x ) = 2о . - 2toi (x ) = 2о . (1 - ro/ x), г, < x< r. (40) При указанных условиях нагружения, закрепления и армирования кольцевых пластин в них реализуется осесимметричный изгиб. На рисунке 3 изображены зависимости от времени t прогиба в точках внешней кромки пластины w(t) = u30(r1, t), вычисленные при q = 150 Па (см. (37)), ю01= ю02 = 0,35 (см. (39)) и радиально-окружной структуре армирования конструкции (см. Рис. 2б и формулы (38), (40) при ф = 0). Кривая 1 получена по классической теории (при этом в (22) и (33) следует принять п = 0 , s(m) = 0 , 0 < m< M = 0), кривая 2 — по теории Рейсснера (п = 0 и M = 0), остальные зависимости с номерами i определены по уточненным теориям при п = 1 и M = 2(i - 3), i > 3 (в частности, 3-я из них рассчитана по теории Редди). Сравнение на рисунке 3 кривых с номерами i > 3 показывает, что с возрастанием значения M, то есть с увеличением числа удерживаемых в разложениях (8), (9) и (11) слагаемых, для рассматриваемой композитной пластины имеет место достаточно быстрая сходимость этих частичных сумм (см. кривые 4–6, которые визуально не различимы). Из рисунка также видно, что вблизи начального момента времени 0 < t< 5 сут наблюдается стадия упрочнения, переходящая в стадию установившейся ползучести, которая для кривой 1 длится вплоть до t = 200 сут (см. Рис. 3б). Однако, согласно поведению кривых 2 6 на рисунке 3а, после t = 20 сут в композитной пластине, при расчете по теориям изгиба, учитывающим ее ослабленное сопротивление поперечным сдвигам, имеет место ускорение ползучести. Именно после t = 20 сут прогибы, полученные по классической теории (кривая 1), существенно отличаются от прогибов, определенных по другим обсуждаемым теориям (линии 2–6), причем это различие быстро возрастает со временем, и уже при t > 40 сут результаты вычислений по классической теории нельзя признать удовлетворительными. Следует подчеркнуть, что нелинейно-наследственная теория ползучести Ю.Н. Работнова описывает только первую и вторую стадии ползучести материала, но не принимает во внимание третью стадию ускоренной ползучести, предшествующую его разрушению [1, 2]. Поэтому ускорение ползучести после t = 20 сут, которое демонстрируют своим поведением кривые 2-6 на рисунке 3, объясняется не началом и развитием предразрушения материалов компонентов композиции, а активным и ускоренным развитием деформаций поперечного сдвига, которые классическая теория не учитывает (подробнее см. ниже). В случае изгибного деформирования балок-стенок, армированных в продольном направлении и изготовленных из нелинейно-наследственных материалов, аналогичные w (t) зависимости, определенные ранее как по классической теории, так и по второму варианту теории Тимошенко (русскоязычное обозначение теории Редди), качественно подобны кривой 1 на рисунке 3 (см., например, Рис. 3 в [17]), то есть для армированных балок-стенок ускорение ползучести не имеет места даже при учете их ослабленного сопротивления поперечным сдвигам. Следовательно, наблюдаемое ускорение ползучести армированной пластины (см. кривые 2–6 на рисунке 3) объясняется более сложным видом напряженно-деформированного состояния (НДС) в компонентах ее композиции (см. (5) и (6)) по сравнению с НДС в фазах композиции армированных балок-стенок (в которых реализуется обобщенное плоское напряженное состояние), а также нелинейным поведением связующего материала — сплава Д16Т (см. (35)). Отметим, что и при других структурах армирования (при 0 < ф < л/2 как при спиральной (Рис. 2а), так и при их спирально-окружной укладке волокон (Рис. 2б)) зависимости w (t) ведут себя качественно подобно кривым, изображенным на рисунке 3. А значит, изучение реономного поведения простейших тонкостенных композитных элементов (продольно армированных балок-стенок) не позволяет выявить все особенности деформирования тонкостенных армированных элементов конструкций более сложной геометрии (в частности, пластин). Кроме того, дополнительные расчеты показали, что при изгибе однородной пластины из сплава Д16Т (ю01=ю02 = 0) также отмечается ускорение ее ползучести, предсказываемое всеми обсуждаемыми теориями, в том числе и классической теорией, которая в этом случае дает вполне приемлемые с инженерной точки зрения результаты по прогибам. Это вновь свидетельствует о значительном влиянии сложного НДС в пластинах на их нелинейно-наследственное поведение при изгибе. Напомним, что кривые 4-6 на рисунке 3 визуально неразличимы, то есть при M > 2 (см. (8)) для пластины из изучаемой композиции практически не наблюдается уточнения решения, поэтому расчет, выполненный при M = 2 (линия 4), в этой задаче условно примем за эталонный. Сравнение ординат правых точек на кривых рисунке 3 б показывает, что к моменту времени t = 200 сут отличие w (t), установленного по классической теории (линия 1), от эталонного решения составляет 99,9%, по теории Рис. 3. Зависимость прогиба в точках внешней кромки кольцевой пластины с радиально-окружной структурой армирования от времени, рассчитанная вблизи начального момента времени (а) и при длительном нагружении (б) по разным теориям: классическая (кривая 1), Рейсснера (2), Редди (3), уточненные теории (4)–(6) Рейсснера (кривая 2) — 36%, а по теории Редди (линия 3) —12%. Следовательно, ни одна из наиболее часто используемых моделей изгибного деформирования тонкостенных элементов конструкций не гарантирует получения традиционной инженерной 5%-ной точности определения прогиба при длительном нагружении рассматриваемой армированной пластины. На рисунке 4 изображены эпюры прогибов, отвечающие начальному моменту времени t = +0 (Рис. 4а) и t = 200 сут (Рис. 4б). Здесь кривые 1 -6 рассчитаны при тех же условиях, что и на рисунке 3, и, согласно их поведению, все анализируемые теории в начальный момент времени предсказывают примерно одну и ту же податливость пластины с радиально-окружной структурой армирования (значения w (+0) отличаются от эталонного не более чем на 2%). Последнее объясняется тем, что анизотропия композиции такой конструкции является слабой (в соответствии с (35) и (36), отношение модулей Юнга волокон Торнел-75 и связующего Д16Т равно 8,2), поэтому даже классическая теория при кратковременном нагружении хорошо описывает изгибное поведение рассматриваемой композитной пластины [28]. Однако поведение кривых 1-6 на рисунке 4б свидетельствует о том, что в момент времени t = 200 сут зависимости и30(т1), предсказываемые разными теориями, сильно различаются, причем не только количественно, но и качественно. Так, поведение кривой 1 на рисунке 4б качественно подобно поведению линий 1–6 на рисунке 4а, а кривые 2–6 на рисунке 4б имеют кривизну, знак которой противоположен знаку кривизны линии 1. Такое необычное поведение кривых 2–6 на рисунке 4б объясняется именно тем, что в окрестности внутренней кромки, которая жестко закреплена, в процессе ползучести в связующем армированной пластины активно развиваются неупругие деформации поперечных сдвигов (подробнее см. ниже). Изменение структуры армирования конструкции может привести и к качественному изменению эпюры ее прогибов. Так, на рисунке 4 кривые 1‘-6‘ рассчитаны для радиально армированной пластины (ф1 = 0 на Рис. 2а) при q = 10 Па и ю01=ю02= 0,35, кривые 1"-5" — для пластины, усиленной в окружном направлении (ф, = л/2) при q = 50 Па и ю1 + ю2+ ю3= 0,7 (см. (39), (40)). Согласно поведению кривых 1 ‘-6′ и 1″–5″ на рисунке 4а, при кратковременном нагружении все обсуждаемые теории и в этих случаях предсказывают примерно одинаковую податливость таких пластин. При длительном же нагружении зависимости и30(х,), определенные по разным теориям изгиба, могут существенно различаться. Так, кривая 1′ на рисунке 4б визуально похожа на линию 1, и ее поведение качественно подобно кривым 1′–6′ на рисунке 4а. Линии же 2′–6′ и 1″–5″ на рисунке 4б качественно отличаются не только от кривых 1 и 1′, но и от 2–6. Действительно, кривые 2′–6′ и 1″–5″ на рисунке 4б имеют ярко выраженную знакопеременную кривизну, причем, согласно поведению линий 1″–5″, в пластине с окружной структурой армирования при ее длительном нагружении максимальный по модулю прогиб имеет место не на внешней кромке (т1 = r1 = 2 м), а в некоторой внутренней точке. Линии 4‘-6‘ и 3'—5" на рисунке 4б визуально неразличимы, следовательно, и в этих случаях расчеты, выполненные при M = 2 (см. (8)), можно условно считать эталонными (кривые 4′ и 4″). Сравнение ординат правых точек на кривых 1′–4′ показывает, что и для радиально армированной пластины при ее длительном нагружении традиционные теории изгиба (классическая, Рейсснера и Редди) не гарантируют достижения 5%-ной инженерной погрешности по прогибу. Судя же по поведению кривых 1″–4″ на рисунке 4б, для пластины, армированной в окружном направлении, теории Рейсснера и Редди обеспечивают вполне приемлемую точность вычислений прогиба, а классическая теория (линия 1″), по сравнению с эталонным расчетом (кривая 4″), дает ошибку более 16%. Рис. 4. Зависимость прогиба кольцевых армированных пластин от полярного радиуса, рассчитанная по разным теориям в два момента времени t : +0 (а); 200 сут (б) Для получения некоторого представления о деформированном состоянии компонентов композиции кольцевой пластины с радиально-окружной структурой армирования в условиях длительного нагружения, предсказываемом разными теориями изгиба при t = 200 сут и q = 150 Па, на рисунке 5 изображены радиальные сечения конструкции и изолинии, на которых интенсивность деформаций s*k) (см. (2)) в к-й фазе композиции (к = 0, 3) имеет постоянное значение. Так как отсутствуют нагружения пластины в радиальном и окружном направлениях, а также в силу равносопротивляемости материалов компонентов композиции растяжению и сжатию (см. (35), (36)) «картины» деформирования фаз композиции симметричны относительно срединной плоскости x3= 0. Поэтому для экономии места на нижних половинах рисунка 5 изображены изолинии деформирования связующего (s*0)= const), а на верхних — армирующих волокон. Сплошные линии соответствуют радиальному семейству волокон: s*1) = е*2)= const (ф = 0 ; см. (38) и Рис. 2), а пунктирные — волокнам, уложенным в окружном направлении (s*3)= const). На рисунке 5а изображены кривые, полученные по классической теории; на рисунке 5б — по теории Рейсснера (здесь сплошные и пунктирные линии на верхней половине рисунка визуально неразличимы); на рисунке 5в — по теории Редди; на рисунке 5г — результаты эталонного расчета (M = 2; см. (8)). Сравнение кривых s*k) = const, приведенных на рисунках 5а и 5б, с эталонными (см. Рис. 5г) показывает, что и классическая теория, и теория Рейсснера не дают даже качественно верного представления о картинах деформирования компонентов композиции рассматриваемой пластины в условиях ее длительного нагружения. Поэтому обе теории неправильно предсказывают и податливость такой конструкции при t = 200 сут (см. кривые 1 и 2 и эталонную линию 4 на рисунке 4б). Сопоставление изолиний s*k) = const (к = 0, 3), изображенных на рисунке 5в, с кривыми на рисунке 5г свидетельствует о том, что теория Редди достаточно грубо предсказывает картины деформирования фаз композиции. Рис. 5. Картины деформирования компонентов композиции кольцевой пластины с радиально-окружной структурой армирования, рассчитанные при t = 200 сут по разным теориям изгиба: классическая (а), Рейсснера (б), Редди (в), уточненной (при M = 2 ) (г) Рис. 5. Продолжение Так, эта теория дает значения е*0), меньшие примерно на 20% (см. нижние части Рис. 5в и 5г), что служит причиной значительного занижения по модулю прогиба, определенного по данной теории при t = 200 сут (ср. кривые 3 и 4 на Рис. 4б). Отметим, что интенсивность поперечной нагрузки q = 150 Па, приложенной к рассматриваемой пластине, является малой. При этом согласно поведению кривой 4 на рисунке 4б, прогиб по модулю также очень мал (не превосходит 3% от толщины пластины). Однако деформации связующего материала в момент времени t = 200 сут весьма значительны и достигают по модулю значений порядка 5% (см. нижнюю часть Рис. 5г). При кратковременном нагружении (t = +0) все анализируемые теории изгиба пластин предсказывают примерно одинаковые картины деформирования компонентов композиции, качественно аналогичные тем, что изображены на рисунке 5а. Изменение структуры армирования пластины может привести к существенному качественному изменению картин деформирования фаз композиции. Так, на рисунке 6 для сравнения приведены эти картины. Они рассчитаны при t = 200 сут и M = 2 (см. (8)) для радиально армированной конструкции (q = 10 Па; Рис. 6а) и пластины, усиленной в окружном направлении (q = 50 Па; Рис. 6б). Этим случаям соответствуют зависимости и30(т,), изображенные на рисунке 4б кривыми 4′ и 4″. Сравнение рисунка 5г и рисунка 6 показывает, что при длительном нагружении пластин с радиальной, радиально-окружной и окружной структурами армирования в компонентах их композиции развиваются совершенно разные деформированные состояния, а значения интенсивности деформаций в связующем могут достигать нескольких процентов. В разные моменты времени исследуем влияние углов армирования φ волокнами спиральных семейств (см. (38) и Рис. 2) на податливость КМ-пластин. В качестве меры податливости изгибаемых пластин примем величину: и3* (t; ф) = max и30(т,, t; ф) r0 < т,< r, I I , t > 0, 0 <ф<л/2. Рис. 6. Картины деформирования компонентов композиции кольцевых пластин с радиальной (а) и окружной (б) структурами армирования, рассчитанные при t = 200 сут по уточненной теории изгиба (M = 2 ) На рисунке 7 изображены зависимости (41) от угла спирального армирования φ в начальный момент времени t = +0 (Рис. 7а) и при t = 200 сут (Рис. 7б). Кривые 1 -4 рассчитаны для пластин со спиральноокружными структурами армирования (Рис. 2б), а линии 1′–4′ — со спиральными структурами (Рис. 2а) при тех же прочих равных условиях, что и кривые 1–4, 1′–4′ на рисунке 4, причем ординаты точек кривых 1′–4′ на рисунке 7а увеличены в 10 раз. Как видно по характеру кривых на рисунке 7, в оба момента времени зависимости (41) в основном являются возрастающими по φ (некоторая немонотонность малой изменяемости наблюдается лишь на правых участках кривых 1′–4′ рисунка 7б), причем наименьшей податливостью обладают пластины с радиальным армированием (см. кривые 1’–4’ на рисунке 7 при ф ^ 0) или с радиально-окружным армированием (см. кривые 1 -4 на рисунке 7 при ф ^ 0). Наибольшей же податливостью обладают либо пластины, армированные в окружном направлении (см. Рис. 7а и кривые 1 -4 на Рис. 7б при ф^п/2), либо конструкции со спиральным армированием, близким к окружному направлению (см. максимумы на кривых 1′–4′ на Рис. 7б). Однако, согласно рисунку 7, изменяемость зависимостей (41) по φ в разные моменты времени количественно существенно разная. Для относительной оценки этой изменяемости рассмотрим величину (umax - umin) t > 0, Au3 (t) = —------—, 3W(12)( u max + u min) где u3max (t )= max u3:(t; ф), 3 0<ф<л/2 3 umin(t )= min u3:(t; ф), t > 0, 3 0<ф<п/2 3 которую назовем относительной изменяемостью податливости. Рис. 7. Зависимость максимального по модулю прогиба кольцевых армированных пластин от угла спирального армирования, рассчитанная по разным теориям в два момента времени t : +0 (а); 200 сут (б) В таблице приведены значения Au3(t), вычисленные для двух моментов времени: t = +0 и t = 200 сут, по разным теориям деформирования пластин при двух типах их армирования, изображенных на рисунке 2. Как видно из рисунка 7 и таблицы, изменяемость податливости пластин, рассчитанная по всем сравниваемым теориям, в зависимости от угла спирального армирования φ с течением времени резко возрастает, и при t = 200 сут она более чем в 20 раз превышает значение в начальный момент времени. Следовательно, при длительном нагружении тонкостенной композитной конструкции ее податливость в существенно большей степени зависит от изменения параметров армирования, чем в случае кратковременного нагружения. Это обстоятельство актуализирует проблему оптимального армирования пластин, работающих в условиях ползучести. Согласно поведению кривых, изображенных на рисунке 7а, классическая теория (кривые 1 и 1’) при всех углах армирования волокнами спиральных семейств (0<ф<л/2) в начальный момент времени обеспечивает вполне приемлемую точность определения податливости рассматриваемых армированных пластин, так как кривые 1 и 1’ лежат близко к эталонным кривым 4 и 4’ (этот результат вполне согласуется с эпюрами прогибов, изображенных на рисунке 4а). Поведение же кривых на рисунке 7б свидетельствует о том, что изменяемость их податливости в момент времени t = 200 сут при 0 < ф < 0,6 рад незначительна, а существенная зависимость u3* от ф (см. (41)) в этот момент времени наблюдается при достаточно Таблица. Относительная изменяемость податливости Ди3 армированных пластин, установленная по разным теориям их изгибного деформирования Рис. 8. Зависимость прогиба АДМ–С-пластины с радиальноокружной структурой армирования от полярного радиуса, отвечающая разным теориям при t = +0 Напомним, что поведение всех кривых на рисунках 4а и 7а свидетельствует: при кратковременном нагружении армированных пластин, состоящих из композиции сплава Д16Т и С-волокон, при заданных уровнях нагружения даже классическая теория обеспечивает приемлемую точность расчета их податливости. Однако этот результат справедлив лишь в случае использования алюминиевого связующего из высокопрочного сплава Д16Т [41]. Дополнительные исследования показали, что при связующем из низкопрочного алюминиевого сплава АДМ даже в условиях кратковременного, но интенсивного нагружения классическая теория дает большую ошибку при определении прогиба по сравнению с теорией Редди. В связи с этим на рисунке 8 приведены зависимости и0 (т1), рассчитанные по разным теориям при t = +0 и q = 1,5 МПа для пластины из АДМ-С-композиции с радиально-окружной структурой армирования (ф = 0; см. (38) и Рис. 2б). Обозначения кривых здесь такие же, как и на рисунке 4. Использовалась идеализированная диаграмма деформирования сплава АДМ с линейным упрочнением и следующими механическими характеристиками [41]: E(0) = 71 ГПа, v(0) = 0,32, ^S”) = 30 МПа, Es(0) = 143 МПа, где ^S”), Es(0) — предел текучести и модуль линейного упрочнения. Расчетную кривую 6 на рисунке 8 условно назовем эталонной, так как дальнейшие уточнения соответствующего решения (при M > 8; см. (8)) приводят к зависимостям и0 (т1), визуально не отличимым от линии 6. Сравнение кривых 2 и 3 (теории Рейсснера и Редди) с линией 6 показывает, что в данном случае обе традиционные неклассические теории неприемлемы для адекватного описания механического поведения такой армированной пластины. Более того, сопоставление кривых 4 и 6 свидетельствует о том, что даже первое уточнение теории Редди (линия 4) не обеспечивает определения неупругого прогиба композитной конструкции с 5%-ной точностью (различие величин (41) составляет около 8%). Поведение кривой 6 на рисунке 8 показывает, что в окрестности внутренней кромки (1 < т1< 1.25 м) кольцевой пластины из АДМ-С-композиции возникает краевой эффект и деформированное состояние, близкое к «срезу» конструкции на опорной кромке в поперечном направлении. 4. Заключение Проведенный сравнительный анализ моделей изгибного деформирования неупругих армированных пластин показал, что из двух традиционных неклассических теорий кинематическая модель Редди лучше описывает поведение композитных тонкостенных элементов конструкций. В ряде случаев неупругого изгиба таких пластин (в том числе и с металлическим связующим) как при их длительном, так и кратковременном нагружении, не только классическая теория, но и теории Рейсснера и Редди не гарантируют достижения требуемой инженерной точности расчетов механического поведения тонкостенных армированных конструкций. Следовательно, для получения адекватных результатов в случае неупругого изгибного поведения волокнистых пластин необходимо использовать уточненные теории высших порядков (например, основанные на кинематических соотношениях (8)–(11) при M ≥ 6 ) особенно в условиях длительного нагружения таких конструкций, поскольку иногда даже при кратковременном нагружении в окрестности опорных кромок могут возникнуть ярко выраженные краевые эффекты, характеризующие «срез» армированных пластин в поперечном направлении, которые либо вообще не обнаруживают, либо плохо отслеживают теории низших порядков. В рамках расчетов по неклассическим теориям изгиба обнаружено ускорение ползучести КМ-пластин при достаточно длительных временах их нагружения, что не имеет места при изгибе простейших тонкостенных конструкций — продольно армированных балок-стенок, изготовленных из тех же материалов фаз композиции. С увеличением длительности времени нагружения изгибаемых КМ-пластин наблюдается существенное увеличение зависимости их податливости от параметров армирования: плотности и направления, что актуализирует проблему рационального и оптимального проектирования КМ-конструкций при их длительном нагружении.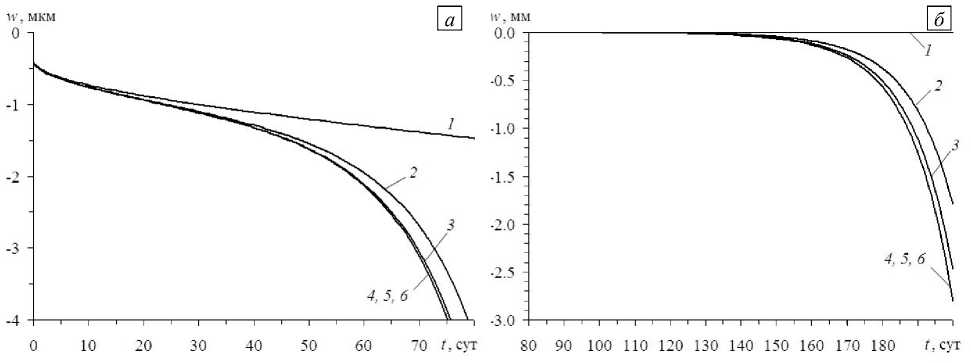
Теория деформирования пластин
Структура армирования
Спиральная
Спирально-окружная
t = +0
t = 200 сут
t = +0
t = 200 сут
Классическая
0,02696
1,9987
0,0788
1,9996
Рейсснера
0,02690
1,0709
0,0777
1,7185
Редди
0,02682
0,9362
0,0775
1,6314
Уточненная (M = 2 )
0,02682
0,8813
0,0777
1,5828
больших углах спирального армирования: л/4<ф<л/2. Кроме того, при этих же углах армирования точность вычисления податливости пластин, определяемой на базе традиционных теорий изгиба, увеличивается (см. кривые 1 и 1’ — отвечают классической теории, 2 и 2’ — теории Рейсснера, 3 и 3’ — теории Редди) по сравнению с эталонными расчетами (линии 4 и 4’). Так, значение и3*, найденное по классической теории для конструкции со спирально-окружной структурой армирования при ф^п/2 (см. кривую 1 на рисунке 7б), отличается от эталонного значения (см. кривую 4 при ф^л/2) всего на 22,2%. При радиально-окружном армировании (ф^ 0) это различие составляет 99,9%. Как уже отмечалось, последний факт объясняется развитием в окрестности внутренней жестко закрепленной кромки значительных деформаций поперечных сдвигов в связующем материале (см. нижнюю часть Рис. 5г).
Список литературы Моделирование неустановившейся ползучести изгибаемых армированных пластин из нелинейно-наследственных материалов
- Работнов Ю.Н. Ползучесть элементов конструкций. -М.: Физматгиз, 1966. -752 с.
- Работнов Ю.Н. Элементы наследственной механики твердых тел. -М.: Наука, 1977. -384 с.
- Никитенко А.Ф. Ползучесть и длительная прочность металлических материалов. -Новосибирск: НГАСУ, 1997. -278 с.
- Радченко В.П., Еремин Ю.А. Реологическое деформирование и разрушение материалов и элементов конструкций. -М: Машиностроение-1, 2004. -264 с.
- Локощенко А.М. Моделирование процесса ползучести и длительной прочности металлов. -М.: МГИУ, 2007. -264 с.
- Голотина Л.А., Кожевникова Л.Л., Кошкина Т.Б. Численное моделирование реологических свойств зернистого композита с использованием структурного подхода//Механика композитных материалов. -2008. -Т. 44, № 6. -С. 895-906.
- Апетьян В.Э., Быков Д.Л. Определение нелинейных вязкоупругих характеристик наполненных полимерных материалов//Космонавтика и ракетостроение. -2002. -№ 3 (28). -С. 202-214.
- Голуб В.П., Кобзарь Ю.М., Фернати П.П. Нелинейная ползучесть волокнистых однонаправленных композитов при растяжении в направлении армирования//Прикладная механика. -2007. -№ 5. -С. 20-34.
- Куликов Р.Г., Труфанов Н.А. Применение итерационного метода к решению задачи деформирования однонаправленного композиционного материала с нелинейно-вязкоупругим связующим//Вычисл. мех. сплош. сред. -2011. -Т. 4, № 2. -С. 61-71.
- Крегер А.Ф., Тетерс Г.А. Применение методов усреднения для определения вязкоупругих свойств пространственно армированных композитов//Механика композитных материалов. -1979. -№ 4. -С. 617-624.
- Крегерс А.Ф., Тетерс Г.А. Структурная модель деформирования анизотропных, пространственно армированных композитов//Механика композитных материалов. -1982. -№ 1. -С. 14-22.
- Янковский А.П. Моделирование механического поведения композитов с пространственной структурой армирования из нелинейно-наследственных материалов//Конструкции из композиционных материалов. -2012. -№ 2. -С. 12-25.
- Кристенсен Р. Введение в теорию вязкоупругости. -М.: Мир, 1974. -339 с.
- Ильюшин А.А. Труды. Т. 3. Теория термовязкоупругости/Составители: Е.А. Ильюшина, В.Г. Тунгускова. -М.: Физматлит, 2007. -288 с.
- Goldhoff R.M. The application of Rabotnov’s creep parameter//Proc. ASTM. -1961. -V. 61.
- Turner F.H., Blomquist K.E. A study of the applicability of Rabotnov’s creep parameter for aluminium alloy//JAS. -1956. -Vol. 23, no. 12.
- Янковский А.П. Анализ ползучести армированных балок-стенок из нелинейно-наследственных материалов в рамках второго варианта теории Тимошенко//Механика композиционных материалов и конструкций. -2014. -Т. 20, № 3. -С. 469-489.
- Янковский А.П. Установившаяся ползучесть сложно армированных пологих металлокомпозитных оболочек//Механика композитных материалов. -2010. -Т. 46, № 1. -С. 121-138.
- Немировский Ю.В. Ползучесть защемленных пластин при различных структурах армирования//ПМТФ. -2014. -Т. 55, № 1. -С. 179-186.
- Reissner E. On bending of elastic plates//Quarterly of Applied Mathematics. -1947. -Vol. 5, no. 1. -P. 55-68.
- Mindlin R. D. Thickness-shear and flexural vibrations of crystal plates//J. Appl. Phys. -1951. -Vol. 23, no. 3. -P. 316-323.
- Васидзу К. Вариационные методы в теории упругости и пластичности. -М.: Мир, 1987. -542 с.
- Баженов В.А., Кривенко О.П., Соловей Н.А. Нелинейное деформирование и устойчивость упругих оболочек неоднородной структуры: Модели, методы, алгоритмы, малоизученные и новые задачи. -М.: Книжный дом «ЛИБРОКОМ», 2012. -336 с.
- Reddy J.N. A refined nonlinear theory of plates with transverse shear deformation//Int. J. of Solids and Structures. -1984. -Vol. 20, no. 9. -P. 881-896.
- Reddy J.N. Energy and Variational Methods in Applied Mechanics. -N.Y.: John Wiley, 1984.
- Амбарцумян С.А. Теория анизотропных пластин (прочность, устойчивость и колебания). -М.: Наука, 1967. -268 с.
- Малмейстер А.К., Тамуж В.П., Тетерс Г.А. Сопротивление полимерных и композитных материалов. -Рига: Зинатне, 1980. -572 с.
- Немировский Ю.В., Резников Б.С. Прочность элементов конструкций из композитных материалов. -Новосибирск: Наука, 1986. -168 с.
- Богданович А.Е. Нелинейные задачи динамики цилиндрических композитных оболочек. -Рига: Зинатне, 1987. -295 с.
- Куликов Г.М. Термоупругость гибких многослойных анизотропных оболочек//Изв. РАН. МТТ. -1994. -№ 2. -С. 33-42.
- Mau S. A refined laminated plates theory//J. Appl. Mech. -1973. -Vol. 40, no. 2. -P. 606-607.
- Christensen R., Lo K., Wu E. A high-order theory of plate deformation. Part 1: homogeneous plates//J. Appl. Mech. -1977. -Vol. 44, no. 7. -P. 663-668.
- Thai C.H. Analysis of laminated composite plates using higher-order shear deformation plate theory and mode-based smoother discrete shear gap method//Appl. Mathematical Modeling. -2012. -Vol. 36, no. 11. -P. 5657-5677.
- Романова Т.П., Янковский А.П. Сравнительный анализ моделей изгибного деформирования армированных балок-стенок из нелинейно-упругих материалов//Проблемы прочности и пластичности. -2014. -Т. 76, № 4. -С. 297-309.
- Янковский А.П. Уточненная модель изгибного деформирования продольно армированных металлокомпозитных балок-стенок, работающих в условиях установившейся ползучести//Математическое моделирование. -2016. -Т. 28, № 8. -С. 127-144.
- Янковский А.П. Сравнительный анализ моделей термоупругопластического изгибного деформирования армированных пластин//Прикладная математика и механика. -2018. -Т. 82, вып. 1. -С. 58-83.
- Карпов В.В. Прочность и устойчивость подкрепленных оболочек вращения. В 2-х ч. Ч. 1. Модели и алгоритмы исследования прочности и устойчивости подкрепленных оболочек вращения. -М.: Физматлит, 2010. -288 с.
- Карпов В.В. Прочность и устойчивость подкрепленных оболочек вращения. В 2-х ч. Ч. 2. Вычислительный эксперимент при статическом механическом воздействии. -М.: Физматлит, 2011. -248 с.
- Янковский А.П. Моделирование ползучести ребристо-армированных композитных сред из нелинейно-наследственных фазовых материалов. 1. Структурная модель//Механика композитных материалов. -2015. -Т. 51, № 1. -С. 3-26.
- Демидов С.П. Теория упругости. -М.: Высш. школа, 1979. -432 с.
- Композиционные материалы. Справочник/Под ред. Д.М. Карпиноса. -Киев: Наук. думка, 1985. -592 с.


