Моделирование нормальной функции лактации человека

Проблема вскармливания детей раннего возраста особенно актуальна сегодня. В настоящее время многие младенцы вскармливаются искусственно [1]. Однако, уже доказана определяющая роль вскармливания первого года жизни в развитии и формировании жевательного аппарата, его строения и функции [2]. Таким образом, существует необходимость в изучении естественного и искусственного вскармливания. Количественное описание первого позволит оценить некоторые параметры, необходимые для моделирования процесса искусственного вскармливания. Полученные результаты могут быть использованы для усовершенствования конструкции соски и бутылочки.

Физиологи разделяют процесс лактации в норме на следующие этапы: молоко образуется в секреторных клетках альвеол, его выработка происходит постоянно и в небольших количествах; затем молоко по системе протоков поступает в молочные синусы, так называемые «хранилища» молока, где оно накапливается до начала кормления [4]. К моменту начала кормления протоковая система железы заполнена молоком. Ребенку для получения молока необходимо лишь преодолеть сопротивление сфинктера в соске. С началом кормления, в первую очередь, освобождаются синусы и крупные протоки. У женщины в момент начала кормления происходит выброс гормона окситоцина, который вызывает сокращение миоэпителия, что стимулирует активное течение молока из альвеол.

Исследования процесса выведения молока у женщин [6] установили, что молоко из молочной железы поступает ребенку не только благодаря разрежению в ротовой полости и стимулам сжатия соска, но вследствие избыточного внутрижелезистого давления (разница между реальным и атмосферным), (рис. 1, а). Измерение

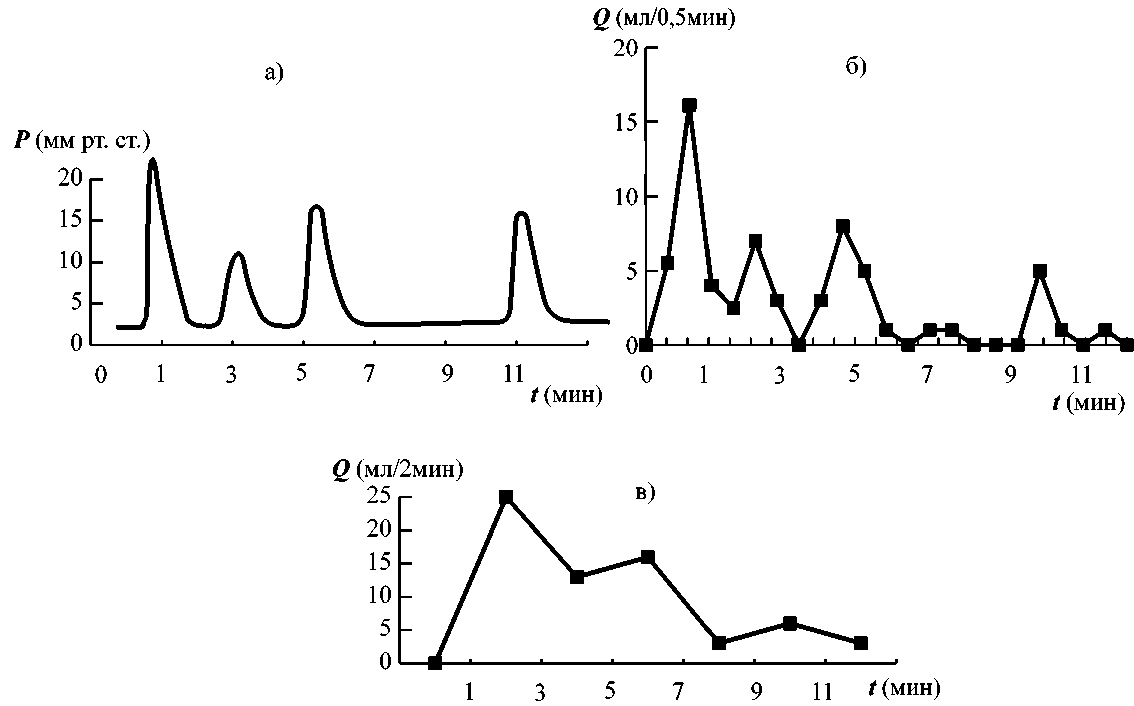
Рис. 1. Внутрижелезистое избыточное давление (а) и скорость выведения молока (б, в) у родильниц в зависимости от времени

P 0 (мм рт. ст.)

-50

-100

-150

0                4

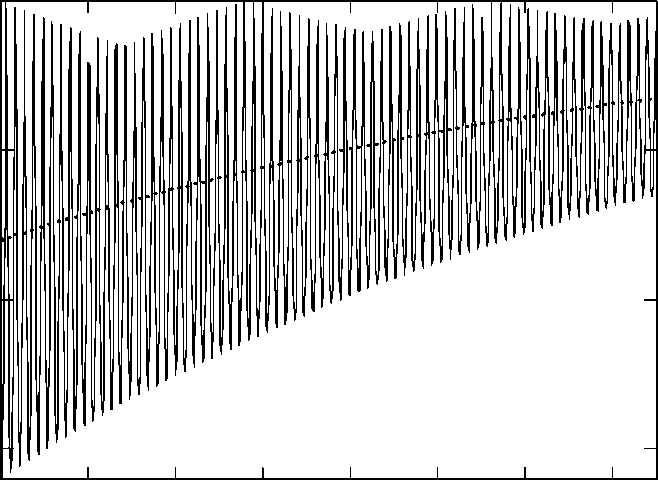
Рис. 2. График зависимости давления внутри ротовой полости у ребенка при естественном вскармливании и осредненного давления от времени

t (мин)

производилось с помощью металлического катетера диаметром 0,65 мм, который вводился в молочный проток на глубину 1,5 – 2 см. Катетер с помощью полиэтиленовой трубки с внутренним диаметром 0,8 мм соединялся с датчиком давления. Рефлекс молокоотдачи, также как и акт сосания, у младенца имеет импульсный характер. Наибольшие пики внутрижелезистого давления приходятся на первые минуты кормления и составляют примерно 2,7 кПа (20 мм рт. ст.). Кроме того,

Альвеолы и выводные протоки из альвеол

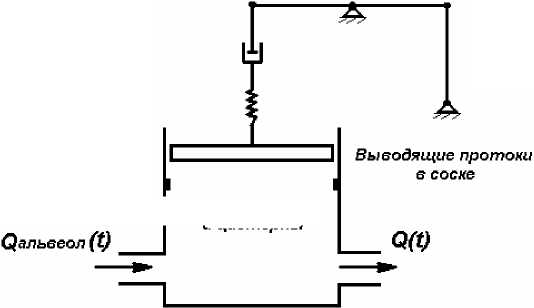
Рис. 3. Схематичное изображение течения молока

Крупные протоки и цистерны была получена расходная характеристика для процесса молоковыведения. Для выведения молока использовался специально разработанный аппарат, с помощью которого подавались пневмостимулы давления и вакуума на сосок и ареолу. Для сбора молока использовался градуированный стеклянный молокосборник емкостью 150 мл с ценой деления 1 мл. Объем молока измерялся каждые 30 с (рис. 1, б) и каждые 2 минуты (рис. 1, в).

Известны также данные о давлении (разница между реальным и атмосферным) внутри ротовой полости ребенка [8] во время естественного вскармливания (рис. 2). Для исследования использовалась силиконовая трубка длиной 15 см с катетером на конце, диаметр которого 0,16 см, и датчик давления. Трубка фиксировалась на груди матери, так чтобы один ее конец был во рту у ребенка во время кормления.

В работе [7] была построена модель молочной железы, позволяющая описать процесс естественного вскармливания и определить коэффициент податливости системы крупных протоков и цистерн, а также гидравлическое сопротивление выводных протоков в соске. При построении модели предполагалось, что коэффициент податливости и гидравлическое сопротивление постоянны во времени и пространстве. Опираясь на известные экспериментальные данные, был предположен вид функции объемного поступления молока из альвеол, усредненной по времени. Также был определен эффективный коэффициент податливости системы крупных протоков и цистерн.

Внутренняя стенка крупных молочных протоков и цистерн [4] имеет складчатую поверхность, слизистая оболочка их выстлана двухслойным цилиндрическим эпителием. Эпителиальный слой слизистой крупных молочных протоков покрыт гладкими мышечными волокнами, располагающимися по спирали и продольно. Миоэпителиальных клеток вокруг крупных протоков уже нет. В устьях последних можно наблюдать утолщения радиального слоя мышечных волокон в виде сфинктеров. Мышечные структуры обладают сократительной способностью, которая зависит от скорости приложения нагрузки. Таким образом, податливость крупных молочных протоков и цистерн и гидравлическое сопротивление протоков в соске изменяются во времени.

Построение математической модели железы

Учтем вязкоупругие свойства молочных протоков. При построении модели сделаны следующие допущения:

• 1)    Все крупные протоки и цистерны объединены в один резервуар с эластичными стенками (рис. 3). Резервуар обладает переменной податливостью, а его гидравлическим сопротивлением пренебрегаем.

• 2)    Система выводных протоков в соске представляет собой недеформируемую трубку. Гидравлическое сопротивление этой трубки велико, а податливостью протоков в соске будем пренебрегать.

• 3)    Податливость резервуара и гидравлическое сопротивление выводных протоков в соске изменяются во времени.

• 4)    Не рассматриваются переходные процессы установления движения молока (ламинарное течение).

• 5)    Система протоков всегда частично заполнена молоком, т.е. резервуар пустым не бывает.

Составим систему уравнений, описывающих процесс:

dV альвеол dt

^- Q ,

dV = d ( С • P ),

Q =

P - Р кон

W ’

dV

Альвеол ⁽ t ) ^{- объемный} расход

где — - скорость изменения объема резервуара, молока, поступающего из альвеол, Q(t) - расход молока в начале выводных протоков в соске, dV - изменение объема крупных протоков, C(t) - эффективная податливость,

P ( t ) - давление в крупных протоках, Р_кон - давление на выходе из жесткой трубки,

W ( t ) - гидравлическое сопротивление мелких протоков в соске.

Первое уравнение системы (1) свидетельствует о том, что скорость изменения объема резервуара равняется разности расходов притока в него молока из альвеол и оттока в выводные протоки в соске. Второе уравнение - это предположение, что изменение объема резервуара зависит от изменения податливости и давления молока в нем. Третье уравнение следует из предположения, что молоко является ньютоновской жидкостью и является результатом реализации течения Пуазейля в жесткой трубке.

В системе (1) экспериментально известны функция расхода молока, вытекающего из соска (рис. 1, б), давление внутри цистерн (рис. 1, а) и давление в ротовой полости ребенка во время естественного вскармливания (рис. 2). Функцию податливости резервуара можно построить, опираясь на физиологию и сделав ряд предположений. Следовательно, нужно определить расход молока, поступающего из альвеол, объем крупных протоков и гидравлическое сопротивление в соске.

Построение функции податливости резервуара

Учитывая складчатое строение молочных протоков железы и сделав ряд предположений, построим функцию податливости. До кормления крупные протоки и цистерны заполнены молоком, следовательно, в терминах предполагаемой модели, резервуар заполнен и растянут, его стенки обладают некоторой малой податливостью. Как известно из эксперимента, к моменту начала кормления происходит расслабление

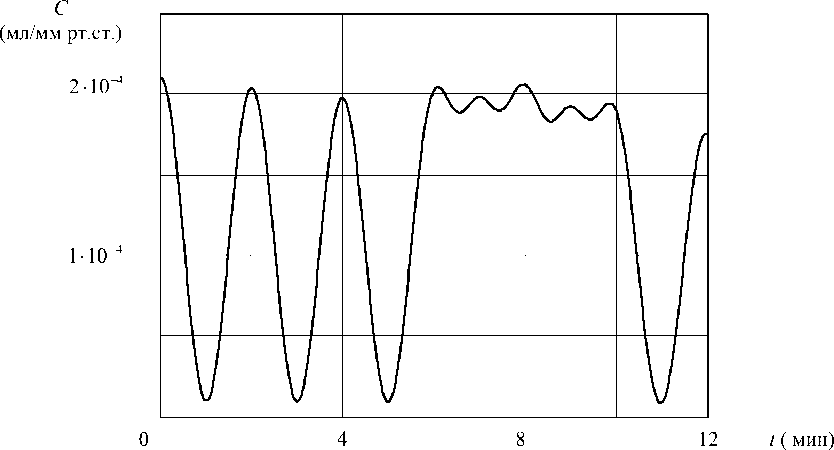
Рис. 4. График податливости резервуара как функции времени гладкой мускулатуры цистерны, т.е. податливость в этот момент увеличивается, что связано с особенностями физиологии молочной железы [5]. Это можно увидеть на рис. 4, при t = 0 мин (начало кормления) податливость резервуара максимальна. С началом кормления происходит выброс гормона окситоцина, что ведет к сокращению миоэпителия, окружающего альвеолы. Это, в свою очередь, способствует активному поступлению молока в крупные протоки и цистерны, т.е. резервуар, который в начальный момент времени оказался неполным, постепенно вновь заполняется, и податливость его уменьшается (при t = 1 мин резервуар заполнен поступившим из альвеол молоком, рис. 4). Затем, во время кормления, резервуар освобождается, его поверхность становится складчатой, и, значит, податливость в этот момент времени большая (t = 2 мин., рис. 4). После освобождения он вновь заполняется, т.е. функция податливости резервуара периодична. Но она должна быть убывающей, так как к концу кормления из альвеол молока поступает значительно меньше, кроме того, мышечная ткань протоков несколько утрачивает способность к расслаблению.

Предполагается, что резервуар заполнен, когда давление в нем максимально (рис. 1, а). Заполненный резервуар обладает малой податливостью.

Исходя из вышеизложенных данных и предположений, построена функция C ( t ) – податливость крупных молочных протоков.

t - m_x                       t - m 2

С ( t ) = ( A • cos(to • t ) + B + ( A + B ) • e ^ + ( A + B ) • e" ) • е "⁰-⁰¹⁵ t ,           (2)

где A = 0,0001, B = 0,00011, to = 3,158, о = 0,41, m₁ = 6,97, m ₂ = 8,96. Коэффициенты идентифицированы в вычислительном эксперименте по соответствию физиологическим данным.

График функции представлен на рис. 4. Отметим, что третий и четвертый члены в скобках обеспечивают приближенное постоянство функции, что соответствует промежутку от 6 до 10 минут на графике давления (рис. 1, а). Последний множитель в выражении (2) дает некоторое убывание функции, экспериментально известно, что напряжение молочной железы к концу кормления увеличивается [5].

Полученная функция C ( t ) имеет максимум при t = 0 равный 0,00021 мл/ мм рт. ст. и минимум при t = 10,944 равный 8,488*10 ^{- 6} мл/ мм рт. ст. Эти значения

Q альвеол

( мл/мин)

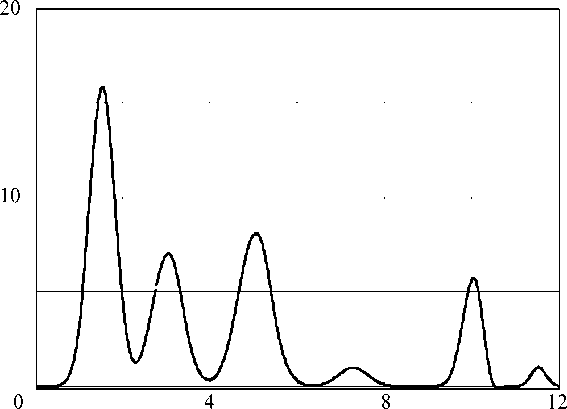
Рис. 5. График функции Q_{альвеол} ( t )

t (мин)

( мл/мин)

Q альвеол

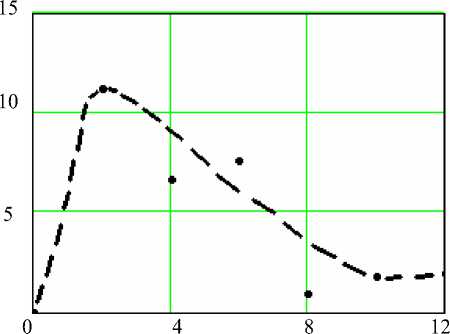
Рис. 6. График функции Q_{альвеол} ( t ) , осредненный по 2 минутам

t (мин)

соответствуют модулю Юнга материала резервуара, равному 6,35*10 7 Па в первом случае и 1,57*10 9 Па – во втором. По литературным данным модуль Юнга для коллагена составляет 109Па, а для эластина – 6*105Па [3], значит, податливость резервуара изменяется от более податливой подобно кровеносным сосудам до менее податливой, как мышечная ткань. Такой диапазон изменения значений модуля Юнга соответствуют известным физиологическим данным для мышечных волокон, выстилающих стенки крупных протоков.

Определение функции расхода молока, поступающего из альвеол

Подставим построенную функцию C ( t ) во второе уравнение основной системы уравнений (1), а затем из первого и второго уравнения определим расход молока, поступающего из альвеол Q_{альвеол} ( t ) :

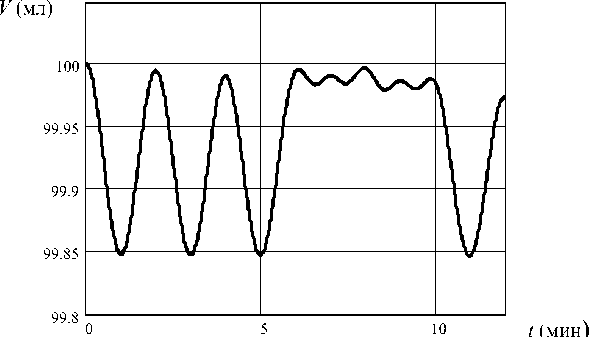
Рис. 7. График изменения объема резервуара

Q— (t) = Q(t) - d(C(t) ' (P (') + Р'Тм ” , (3) dt где Р(t) и Q(t) - экспериментально известные функции, но Р(t) - избыточное давление, поэтому к нему добавлено атмосферное давление (рис. 1, а, б, соответственно), Ратм = 760 мм рт. ст.

График функции представлен на рис. 5. Q_QЛ bвeo _Л ( t ) удовлетворяет физиологическим процессам, которые происходят в молочной железе во время кормления. Из альвеол поступает молоко в больших количествах в первые минуты кормления, так как оно накопилось в них в промежутке между кормлениями. Затем, после сокращения миоэпителия, молоко вырабатывается в секреторных клетках и накапливается в альвеолах до следующего сокращения. Вполне естественно предположить, что со временем молока вырабатывается меньше, а паузы между сокращением миоэпителия становятся больше. Значит, полученный результат соответствует физиологии.

Также осредненная по 2 минутам кривая (рис. 6) похожа на уже ранее построенную функцию Q_onbeeon ( t ), исходя из некоторых предположений и известных экспериментальных данных [7].

Проинтегрировав второе уравнение системы (1), можно определить изменение объема резервуара (рис. 7):

V ( t ) = V 0 + C ( t ) . ( Р ( t ) + Р атм ) - C (0) . ( P (0) + Р атм ) , (4)

где, исходя из некоторых физиологических данных, предположено, что V ₀ = 100 мл, C (0) = 0,00021 мл/мм рт. ст. - податливость резервуара при t = 0 мин (рис. 4), Р (0) = 0,56 мм рт. ст. - давление в крупных протоках и цистернах при t = 0 мин (рис. 1, а). Объем также изменяется периодично, но с небольшой амплитудой, так как расход молока, поступающий в резервуар, почти совпадает с расходом молока, которое вытекает.

W 400

мм рт. ст. • мин мл

г

4                     8                   12

t (мин)

Рис. 8. График зависимости гидравлического сопротивления в соске от времени

Определение сопротивления в выводных протоках

Для дальнейшего моделирования искусственного вскармливания необходимо определить гидравлическое сопротивление в выводных протоках в соске W ( t ) .

Рассмотрим последнее уравнение системы (1):

Q =

P - Р кон

W ^,

здесь P_кон – давление на выходе из соска (в ротовой полости ребенка). График этой функции экспериментально определен [8] (рис. 2). Установлена аналитическая зависимость осредненной по времени функции давления внутри ротовой полости ребенка во время кормления (рис. 2):

р_о „=- 80 • е     .                                   (6)

кон

Из уравнения (5) можно найти сопротивление:

р-р

W ( t ) =     QP . ,                                          (7)

график W ( t ) представлен на рис. 8. Полученная величина W ( t ) в выводных протоках в соске достаточно хорошо описывает процесс работы сфинктера в соске, большие пики сопротивления соответствуют его закрытию, а минимальные значения – тому значению, которое преодолевает ребенок при сосании.

Сделаем некоторую оценку полученных локальных минимумов коэффициента сопротивления (рис. 8).

Рассмотрим значения W mi _n1 = 4,6977 мин*мм рт. ст./ мл = 3,76*10¹⁰Па*с/м³ при t = 1,52 мин., и W min ₂ = 52,333 мин*ммрт. ст./ мл = 41,86*10¹⁰Па*с/м³при t = 7,26 мин., соответствующие пикам, когда молоко поступает из груди в ротовую полость ребенка (рис. 8).

Оценим эффективный радиус отверстия в соске по этим данным согласно формуле Пуазейля:

• I 8 • n • l

  
  

N n • W ’ где примем l = 0,01 м - длина выводного протока в соске, опираясь на известные физиологические данные [4], и n = 2*103 Па*с - известная вязкость грудного молока [4].

Полученные результаты R mi _n1 = 0,1 мм, R _min2 = 0,2 мм довольно достоверны.

Выводы

Построена математическая модель функционирования молочной железы в норме. Такая модель позволяет изучить и объяснить процесс естественного вскармливания младенца. Определены функция, описывающая процесс выработки молока Q_{альвеол} ( t ) , эффективная податливость крупных молочных протоков С(t) и сопротивление выводных протоков в соске W ( t ) . В дальнейшем эти результаты будут использоваться при проектировании соски для искусственного вскармливания.