Моделирование одиночного сокращения скелетной мышцы

В литературе для описания сокращения волокна скелетной мышцы, которое содержит достаточно большое число саркомеров (для портняжной мышцы лягушки эта величина порядка 105), используется простейшая модель Хилла [1] или ее различные модифи- кации [2–7], так как клеточные модели, представленные, например, в классических работах [8–13] и в более новых [14–20], описывающие сокращение каждого саркомера в отдельности, формально требуют для такой задачи учета сокращения всех саркомеров. Основным ограничением модели Хилла и ее модификации является отсутствие явного описания сократительного

Эта статья доступна в соответствии с условиями лицензии Creative Commons Attribution-NonCommercial 4.0 International

License (CC BY-NC 4.0)

This work is licensed under a Creative Commons Attribution-NonCommercial 4.0 International License (CC BY-NC 4.0)

элемента [21], который непосредственно отвечает за сокращение путем воздействия на нее со стороны центральной нервной системы (ЦНС) через мотонейроны. По этой причине описание подходом Хилла одиночного режима сокращения мышечного волокна, когда мышца возбуждается одиночным спайком, неудовлетворительно.

В работах [18; 19] представлена модель сокращения сердечной мышцы. Идеи, заложенные в ней, использованы в [22] для построения модели сокращения скелетной мышцы. Она учитывает кальциевые механизмы сокращения и представляет мышцу как комплекс активных двигательных единиц (саркомеров). Входом является средняя скорость притока ионов кальция в мышечную клетку. Основным ограничением является требование ко входному сигналу: входной сигнал должен быть «медленно» меняющейся гладкой функцией, характерные времена изменения которого должны быть равны или превосходить характерные времена рассматриваемого движения. Поэтому использование данной модели оправданно для сокращения в условиях гладкого тетануса. В работе [22] рассматривается как раз этот случай, когда на нагруженную постоянной нагрузкой мышцу подается сигнал из спайков с частотой, необходимой для образования гладкого тетануса. Показано, что модель работает, если в нее подается уже осредненный сигнал по всей мышце.

В данной работе обсуждается применение подхода [22] для описания одиночного сокращения, когда входом является одиночный спайк. Формально реакция данной упрощенной модели на такое возмущение на временах переходных процессов не обязана совпадать с откликом мышцы на данное одиночное возмущение с математической точки зрения. Но так как возмущение действует непосредственно на медленную переменную и поскольку модель строилась как набор последовательных приближений, представляется возможным посмотреть реакцию модели на одиночное возмущение для менее грубых упрощений, которые также представлены в работе [22]. Анализ отклика на одиночное возмущение будем проводить для портняжной мышцы лягушки, поскольку для нее в литературе представлены обширные экспериментальные данные о таком сокращении [23-28].

Материалы и методы

Модель сокращения волокна скелетной мышцы

Рассмотрим модель, описанную в [22]:

F a = , I EN xb NW ( l s ) n^ + ⁰ - ),

N i(1)

^ = f+(Ф (3i)( Ai-n)-nG (Si)), dδ

dt

= — v - 3,. Ф (3,.) f+

2h s     ii)

- n.

ni

W ( l s ) =

1 - k J l l ‘ l    ^ls 0,1

s 0,1

1, l s e ( l s 0,1 , l s 0,2 ]

,

1 - k ,,2

^ls    ls 0,2

ls 0,2

, l s >  l s 0,2

d dt

Ф ( ³ ) =

( s . - s ) ²

,3 >  0,

' b + c 3², 3 <  0

G (3) = ]

• 3.    - 3

d0 = fA.1 + e '" (3i)-0i)• dA dt

- а ( n 0;) — m

:₊l c (1 - — ) m

de X ⁽ ci ) dc

= Q i ( t ) -

^k ( c i ^{- c} * ) 2    Gn d- i

c i ⁺ k k

C dt ^,

X ( c ) = ^{1 +}

Bk B

( c ^{+ k}B ) ²

,

где Fa - активная сила, создаваемая актинмиозиновым комплексом, S - площадь «поперечного сечения» мышцы, N - число саркомеров в поперечнике, E - жесткость миозиновых мостиков, Nxb - количество головок миозина, приходящихся на половину длины миозиновой нити, Nm - количество миозиновых нитей на единицу поперечного сечения саркомера, ni - доля миозиновых мостиков в i-м саркомере, присоединенных к актину, 3, - среднее по ансамблю безразмерное смещение миозиновых мостиков после их присоединении к актину в i -м саркомере, 0, - доля мостиков, находящихся в состоянии генерации силы в i-м саркомере, h - перемещение головки миозина в состояние генерации силы, W (ls) - безразмерная длина зоны перекрытия в половине длины саркомера, ls - длина саркомера, f+ - скорость присоединения-миозновых мостиков в начальный момент времени; 3. - максимальное значение 3, во время растяжения, b, c, у - константы, — - максимальная вероятность присоединения мостиков в i-м саркомере, с, - безразмерная концентрация кальция в i-м саркомере, m и kn - параметр аппроксимации Хилла зависимости «сила – концентрация кальция» и «степень зависимости связывания Ca2+ c тропонином от количества присоединенных к актину миозиновых головок» соответственно, B – полная безразмерная концентрация кальциевого буфера в мышечных клетках, kB – нормированная постоянная равновесия буфера, λ – скорость откачки кальция в саркоплазматический ретикулум, c – нормированная концентрация кальция в расслабленной мышце, C – концентрация тропонина, C – концентрация кальция, соответствующая полунасыщению тропонина, а — ск°-рость перехода тропомиозина в открытое состояние после того, как тропонин связался с кальцием, k – константа, Q (t) - скорость притока ионов кальция в саркомере. Значения параметров приведены в работе [22].

Анализ системы (1) и ее применение в прикладных задачах достаточно затруднительно ввиду большого числа саркомеров в поперечном сечении мышцы (диаметр саркомера для скелетных мышцы человека в среднем составляет примерно 1 мкм [29], значит, площадь сечения саркомера можно оценить примерно как 0,785 мкм², тогда для камбаловидной мышцы человека с максимальной площадью в поперечнике 41 см² [30] получим порядка 10⁸ саркомеров). Поэтому в работе [22] предложен подход на основе методов разделения движения [31; 32] для упрощения (1). Опишем коротко данный подход. Характерные времена переменных n i , δ , θ , A , c i в системе (1) разнесены на несколько порядков [22]: характерное время изменения доли присоединенных мостиков в саркомере t 3 равно 0,005 с; характерное время смещения миозиновых мостиков t 2 равно 0,01 с; характерное время перехода мостиков в состояние генерации силы в саркомере t 4 равно 0,0004 c; характерное время изменения степени активации t 1 равно 0,2 с; характерное время изменения концентрации кальция t 0,5 c. Это обстоятельство позволило в (1) выделить иерархию малых параметров и использовать методы фракционного анализа [31; 32] для построения упрощенных моделей на базе системы (1). В этих моделях пренебрегается быстрыми движениями различного темпа. В модели

F a =

^S        2 ^W ( ls ) Ф

N i        Ф ( 8_t ) + G ( 8_; )

ф (^s,) A

n. =--------------------.

'   Ф (§,) + G (8,)

vs

А .

—

• ¹8,    G (§, ) = 0, А. = —¹— , b ^{( 1} )             2 f , + h’

0,= 0o (§/), c (1 — A)m — a(n9;)Am = 0, do = _L (Q (t) — ■        1

dt x( c ) Г     ( c : + k ,.) 1

сохранены только дифференциальные уравнения, описывающие изменение концентрации ионов кальция на временах порядка 0,5 с. В модели

SEN -     .ФММ)

• ■        n ^{2    ( s )} Ф (S~) + G ( 8 i ) i -

• _ Ф (s’) A

n   Ф (s’) + G (s’) ’ v-—1 s’G (s’ ) = 0, А* b i''

0" = 00 (s’), dA     f^

“X = a +1 с(1—A)m— a(n0i)Am I, dt      ^j dc, = 1 L z. ^( c,— c*)2 -Ct^ ] dt X(c,) I         (c,2 +k*)    Со dt J

также сохранено описание динамики присоединения мостиков, имеющее характерное время порядка сотой доли секунды. Это добавляет в систему дополнительную нелинейную дифференциальную связь, которая усложняет систему и ее поведение, но которая позволяет описывать процесс сокращения на временах меньших, чем это позволяет делать модель (2), что будет показано дальше. А* - это характерная скорость сокращения саркомера, переменные ni, δ , θ , A – это переменные, приближенно описывающие изменение соответствующих величин ni, δ , θ , A – для выбранных диапазонов времени описания процесса в модели. Системы (2), (3) в представленном виде неприменимы для прикладных задач ввиду большого числа саркомеров в мышце, динамика каждого из которых описывается своей системой уравнений. Используя соотношения:

^l s ~_N ’ ^{N sarc} ~ o ’ v s Xv '  ’

1 v sarc                 z 0                sarc

где L – длина мышцы, l 0 – средняя длина саркомера, L 0 – длина мышцы в нерастянутом состоянии, N sarc – число саркомеров вдоль мышцы, можно построить упрощенные модели сокращения, которые уже могут быть применены в приложении. Переход от описания сокращения единичного саркомера к описанию сокращения мышцы будем проводить, формально изменив в рассмотренных уравнениях смысл индексируемых переменных.

В этом случае вероятности окажутся замененными на средние значения соответствующих величин, имеющими те же обозначения, но лишенные индекса. Так, для системы (2) получим упрощенную модель, которая приближенно описывает сокращение на временах порядка 0,5 с:

Для дальнейшего изложения (5), (6) назовем «упрощенная модель I» и «упрощенная модель II» соответственно. Дополнительно рассмотрим модель одного саркомера, которая получается из (1) формальной подстановкой N равно 1 и заменой суммы по саркомерам на одно слагаемое:

( J А Ф ( 5 )( 5 + 0)_

F a = ^SEN xb ^N m ^hW —        Д ^A ,

V N sarc ) Ф ( 5 ) + G ( 5 )

_    Ф (5) A n   Ф (5) + G (5),

F_a = SEN xb N m hW ( l s ) n ( 5 + 0 ) , dn = f , + ( Ф ( 5 )( A - n ) - nG ( 5 ) ) ,

d 5 dt

= ^Ev. - ^5ф ( ⁵ ) ^f *

A - n , n

vs

Л *

- 1 5G ( 5 ) = 0, у b

- I L dt

V sarc

,

d 0 dt

= f + ( 1 + e -⁵ )(0_O ( 5 ) - 0),

0 = 0 0 ( 5 ) ,

c (1 - A ) m - a( n 0)( A ) m

dA    I .

— = a₊ l c (1 - A ) ^m dt        I

- a( n 0) A^m

= 0,

dc =  1   Q (t) - dt   X(c),

X( c - c * )^{2 ( c 2 +} k x )

X^{( c} ) dc = ^{Q (} t )

dt

X( c - c, )² ( c ² + k x )

^C Tn ^dA

Co dt ’

,

A = - У A , N i ⁱ

где n - средняя доля миозиновых мостиков в мышце, присоединенных к актину, 5 - среднее по ансамблю безразмерное смещение миозиновых мостиков после их присоединении к актину, 0 - средняя доля мостиков, находящихся в состоянии генерации силы, A - средняя максимальная вероятность присоединения мостиков в мышце, c - средняя безразмерная концентрация кальция в мышце, Q ( t ) - средняя скорость притока ионов кальция в мышце.

Для системы (3) получим упрощенную модель, которая приближенно описывает сокращение на временах свыше 0,2 с:

( _т А Ф ( 5 )( 5 + 0)_

F a = ^SEN xb ^N m ^hW\ _у I4A-4 A , V N sarc ) Ф ( 5 ) + G ( 5 )

_    ф (5) A n   Ф (5) + G (5),

где переменные n i , 5, , 0, , A_; , c i заменены на n , 5 , 0 , A , c соответственно. Такую модель назовем полной.

Для упрощенной модели I в [22] показано, что она может описывать с погрешностью порядка 5 % тетаническое сокращение, если в качестве входа Q ( t ) использовать среднее по ансамблю всех двигательных единиц и по времени воздействие при частотах импульсации порядка 30 Гц. В данной работе будет рассматриваться сокращение после одиночного импульсного воздействия, продолжительность которого на 2 порядка меньше характерного времени системы 0,5 с. Такое воздействие нельзя отнести к медленным, однако по завершению переходного процесса, вызванного единичным импульсом, предлагаемые упрощенные модели должны корректно описывать развитие суммарного накопления изменений.

v s- - ¹ 8G (5) = 0, Л * b ^u

d I L v = — — s sarc

,

0 = O o ( 5 ) ,

I-

— = a+ c(1 - A) m - a(n0)(A) m, dt)

dc _  1   —    X(c - c*) CTndA

1               ^{Q (} t )      ^_2

dt   X(c) V       (c + k)   C0

Моделирование сократительной реакции мышцы на одиночный импульс

Применим упрощенные модели I и II для построения одиночного сокращения. Рассмотрим сокращение портняжной мышцы лягушки в двух режимах - в изометрическом и изотоническом. Нерастянутую длину L 0 возьмем равной 3 см [25]. Число саркомеров вдоль мышцы N _sarc найдем из соотношения (8):

N sarc = у = 15 000, l ₀

где 1 0 - средняя длина саркомера в мышце. Для описания пассивных сократительных свойств, как и в [22],

введем пассивную составляющую усилия F p . Тогда сила мышцы F будет складываться из двух компонент (9), пассивной F p и активной F a , задаваемой системой (5) или (6).

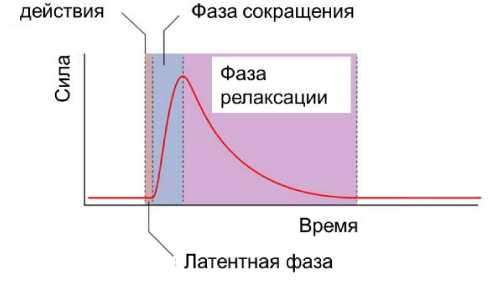
Мышечное сокращение на возбуждение одиночным импульсным воздействием описывается тремя фазами [35] - латентной фазой, фазой сокращения и фазой релаксации на рис. 1.

F p = k ( L - L_o), ^F = F p + F a ,

Изометрический режим сокращения

где k - это пассивная жесткость мышцы. Значение пассивной жесткости возьмем равной 84 Н/м из работы [33]. Площадь поперечного сечения мышцы лягушки S рассчитаем из соотношения (10):

S = M- , (10) ^{р L} 0

где M - масса портняжной мышцы лягушки, р - плотность портняжной мышцы лягушки. Значение плотности портняжной мышцы лягушки возьмем из [34], где р равно 1,035 г/см³. Масса мышцы лягушки M равна 35 мг [25]. Тогда площадь поперечного сечения S можно имеет примерное значение 0,0113 см².

Рассмотрим изометрический режим сокращения. Для такого режима длина мышцы будет постоянной, и мышечное сокращение будет описываться системами (5), (6), (11).

L ( t ) = L o -                           (11)

Для описания одиночного сокращения требуется определить вход Q(t). Строго говоря, одиночное сокращение - это одиночный спайк, который приходит от ЦНС на мотонейрон. В результате этот сигнал провоцирует выброс ионов кальция в мышечные клетки. Поэтому скорость притока ионов кальция Q(t) связана с потенциалом на мотонейроне V [36]:

Q ( t)~ V -

Потенциал

Точная зависимость между притоком кальция и потенциалом на мотонейроне неизвестна, поэтому будем рассматривать гладкую зависимость между притоком ионов кальция и потенциалом на мотонейроне, качественно соответствующую данным из [36]:

( t - 1 0 )² --7-----

Q ( t ) = Q * e ²°^Q A t ,

где Q - это максимальное значение среднего притока ионов кальция, t - это середина интервала воздействия, A t = 5 мс - продолжительность импульсного воздействия [36], и g_q = A t /6.

Рис. 1. Качественное поведение мышечного сокращения в результате одиночного импульсного воздействия [35]

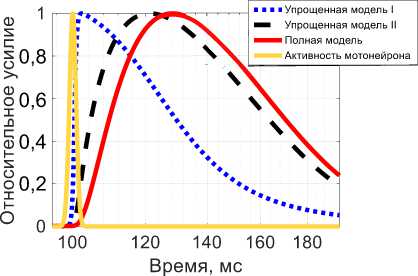
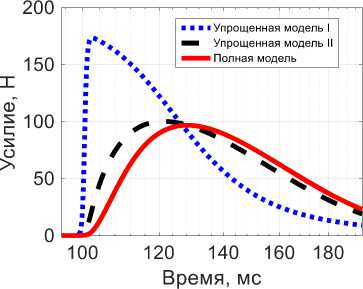
Рис. 2. Активная сила при изометрическом сокращении в ответ на одиночный импульс Q : красная линяя (сплошная) - результат полной модели, синяя линяя (точки) - результат упрощенной модели I, черная линяя (тире) - результат упрощенной модели II, желтая линяя (сплошная) - импульсное воздействие

На графиках рис. 2 и 3 представлены результаты моделирования реакции полной модели и упрощенных моделей I и II на одиночный импульс, задаваемый Q .

Значение t ₀ = 0,1 c, величина Q* = 2 - 10⁴ с^-1 выбрана таким образом, чтобы максимальная величина концентрации ионов кальция при сокращении была в диапазоне от 5 до 10 мкмоль (рис. 3), что обычно и наблюдается при сокращении мышцы в результате одиночного импульса [24].

Для полной модели в сокращении присутствуют три фазы сокращения – латентная фаза, фаза сокращения и фаза релаксации. Латентный период длится порядка 1 мс, фаза сокращения – порядка 30 мс. Для упрощенной модели I латентный период и период сокращения практически отсутствуют (рис. 2), а сразу после окончания воздействия начинается период релаксации. Более того, поведение упрощенной модели I разительно отличается от поведения полной модели.

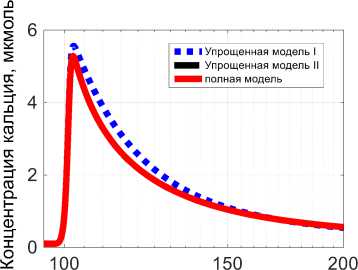
Рис. 3. Концентрация кальция в мышце при изометрическом сокращении в ответ на одиночный импульс Q : красная линяя (сплошная) – результат полной модели, синяя линяя (точки) – результат упрощенной модели I, черная линяя (тире) – результат упрощенной модели II

Эти обстоятельства делают упрощенную модель I применимой только для описания релаксации. Такое расхождение вызвано тем, что упрощенная модель I применима на временах порядка 0,5 с, что существенно больше, чем время импульсного воздействия A t . Для упрощенной модели II, наоборот, присутствует латентный период порядка 1 мс, и период сокращения ярко выражен. Время достижения пика сокращения составляет порядка 20 мс (см. рис. 2), что по порядку величин совпадает с данными мышечного сокращения [23; 28]. Хотя упрощенная модель II формально применима на характерных временах, превышающих 0,2 с, но ввиду наличия еще одного дифференциального нелинейного звена, она может качественно и количественно описывать одиночное сокращение [23; 26–28].

Изотонический режим сокращения

Рассмотрим изотонический режим сокращения. Для изотонического сокращения будем рассматривать мышцу, воздействующую на груз массы M , один конец которой жестко закреплен, а другой находится под воздействием постоянной силы P . Тогда уравнение движения мышцы будет иметь вид (14),

Mx = р - F , F = F p + F ,

где F – сила, создаваемая мышцей, которая складывается из, Fp – пассивной составляющей силы (9) и Fp – активной составляющей силы, в соответствии с (5),  (6) при x = L. Параметры моделирования задаются такие же, как и для изометрического сокращения, внешнюю силу P примем равной 0,0294 Н, что соответствует весу груза массой 3 г. Результаты моделирования представлены на графиках рис. 4 и 5.

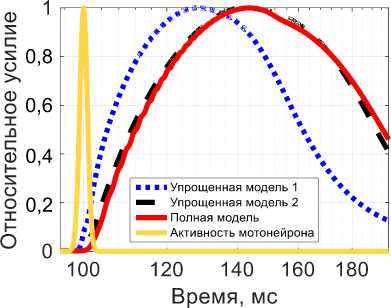
Рис. 4. Активная сила при изотоническом сокращении в ответ на одиночный импульс Q : красная линяя (сплошная) -результат полной модели, синяя линяя (точки) – результат упрощенной модели I, черная линяя (тире) – результат упрощенной модели II, желтая линяя (сплошная) – импульсное воздействие

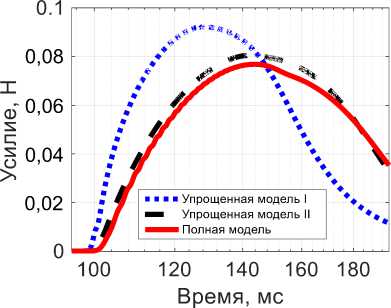
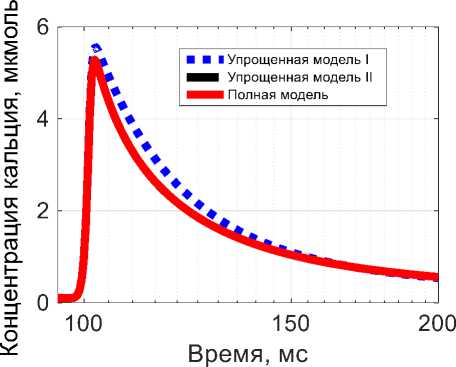
Рис. 5. Концентрация кальция в мышце при изотоническом сокращении в ответ на одиночный импульс Q : красная линяя (сплошная) – результат полной модели, синяя линяя (точки) – результат упрощенной модели I, черная линяя (тире) – результат упрощенной модели II

Для случая изотонического сокращения полная модель также воспроизводит качественно поведение мышцы при одиночном импульсном воздействии, причем фаза сокращения длится около 45 мс, а положительность латентного периода соизмерима с длительностью импульса на мотонейроне. Поведение упрощенной модели I для изотонического сокращения отличается от поведения упрощенной модели I для изометрического сокращения. Для упрощенной модели I наблюдается характерное сокращение с пиком максимального сокращения через 30 мс, что по порядку совпадает с данными из [23; 28]. Также для нее видна небольшая латентная фаза. Но для упрощенной модели I все еще видны существенные отличия от полной. Для упрощенной модели II время сокращения составляет порядка 40 мс, что достаточно хорошо соответствует экспериментальным данным для времен сокращения [23; 28]. Более того, поведение упрощенной модели II качественно повторяет поведение полной, чего не было для изометрического сокращения. Все модели качественно повторяют экспериментальную зависимость реакции мышечного волокна на одиночный импульс [23; 26–28].

Отличие между изометрическим и изотоническим сокращением состоит в изменяющейся длине мышцы. В случае изометрического сокращения длина постоянна, а значит, средняя длина саркомера ls = L/Nsarc тоже постоянна. Поэтому часть переменных остаются постоянными: δ , θ . В случае изотонического сокращения, появляется еще дополнительное дифференциальное уравнение в системах (5), (6), что усложняет описание поведения системы, так как появляется дополнительная нелинейная связь между параметрами сокращения и длиной мышцы. Изменение концентрации кальция при изотоническом сокращении практически осталось таким же, как и в изометрическом сокращении, поскольку длина саркомера в уравнении на концентрацию ионов кальция влияет опосредованно на изменение концентрации кальция.

Заключение

Исследовалось поведение упрощенной модели скелетной мышцы [22] в ответ на импульсное воздействие, то есть одиночное сокращение, в двух режимах сокращения – изометрическом и изотоническом. Хотя изначально упрощенные модели I и II строились для описания тетанического сокращения порядка 0,5 и 0,2 с и выше соответственно и формально описывают установившиеся процессы на этих временах, но не описывают переходные процессы на меньших временах, подход, предложенный в [22] для построения упрощенной модели, позволяет описывать реакцию мышцы на одиночное импульсное воздействие, длительность которого составляет 5 мс с помощью модели II.

Дополнительным применением упрощенной модели II видится возможность анализа зависимости между активностью мотонейрона и концентрацией ионов кальция в мышце. Поскольку выходом упрощенной модели II является мышечное усилие, можно измерить силу в процессе сокращения, миографическую активность и попытаться восстановить усилие по миограмме, подобрав некоторую зависимость между миограммой и скоростью притока ионов кальция.

Упрощенная модель II состоит из двух нелинейных дифференциальных звеньев, учитывает изменение кальция в мышце в ответ на одиночное импульсное воздействие (спайк), создаваемое ЦНС, и может описывать сокращение на такое воздействие. Характерные времена сокращения для такой модели соизмеримы с характерными временами одиночного сокращения, данные по которым представлены в литературе для портняжной мышцы лягушки [23; 28].