Моделирование отклика микроферрогеля на внешнее магнитное поле

Магнитные полимерные микрогели или микроферрогели (МФГ) — это сверхминиатюрные объекты, которыми можно управлять посредством приложенного извне магнитного поля. Если компоненты МФГ прочно связаны друг с другом (например, наночастицы ферромагнетика химически сшиты с полимером), приложенное поле способно не только перемещать объект как целое, но также позволяет модулировать его форму, структуру и объём. Благодаря этим особенностям, МФГ — предмет большого интереса для тераностики и наномедицины, где предполагается использовать их в качестве контейнеров для доставки лекарств, нанохирургических инструментов и манипуляторов, и другого [1–4].

Активные экспериментальные исследования в указанном направлении начались сравнительно недавно и сразу вызвали большой интерес. Отметим значительные успехи в области синтеза водных МФГ с различными химическими составами сетки и наночастиц. Но, как это часто бывает, прорыв в эксперименте привёл к тому, что накопленный в наблюдениях объём информации пока слабо систематизирован. Для понимания нужны модельные представления, обладающие достаточным уровнем общности, которые на сегодняшний день отсутствуют. Следовательно, в той области науки о мягком веществе, которая призвана изучать МФГ, остро стоит вопрос разработки моделей упомянутых объектов, где бы явно учитывалась их специфика: взаимное влияние полимерной сетки и наночастиц и, конечно, взаимодействие наночастиц с приложенным магнитным полем.

Выбор адекватного способа описания МФГ, на взгляд авторов предлагаемой вниманию работы, довольно очевиден. Малый размер образца означает, что в его состав входит, хотя и значительное, но счётное число элементов — полимерных звеньев и наночастиц. Отсюда следует, что наибольшего успеха в решении задач данного класса можно добиться с помощью современных методов многочастичного компьютерного моделирования [5], то есть при рассмотрении изучаемого объекта как совокупности взаимодействующих «элементарных» частиц. Таким образом, указанный метод в его модификации, называемой крупнозернистой молекулярной динамикой, используется для описания структурных изменений, которые происходят в модельном МФГ при его намагничивании. Конкретная цель публикации — показать, как влияют концентрация наночастиц, их магнитные свойства и характер взаимодействия с полимерным гелем на структурный и механический отклики микрообъекта.

2.    Модельный микроферрогель

В методе крупнозернистой молекулярной динамики, прежде всего, следует конкретизировать, из каких элементов конструируется модельный образец. В обсуждаемой задаче предполагается, что МФГ состоит из бесструктурных элементов двух типов: 1-й — монодисперсные сферические однодоменные частицы ферромагнетика; 2-й — монодисперсные сферические «мономеры» полимерной сетки. Под «мономером» здесь понимается некоторый многоатомный фрагмент макромолекулы (блоб), который при рассмотрении динамики системы можно считать неделимой структурной единицей [6]. Взаимодействия между указанными элементами описываются с помощью межчастичных потенциалов. Так, взаимную непроницаемость для всех элементов ансамбля обеспечивает так называемый урезанный потенциал Леннард-Джонса [7]:

U L ( r j H

4s

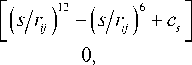
0 < rj < R cutoff, у > P rj — 1 Vcutoff ,

где r — расстояние между частицами i и j ; R _cutof f = ( d i + d_j ) /2 — расстояние, равное полусумме диаметров частиц, на котором их взаимодействие урезается; s и 5 = 2 -16 R _cutoff — параметры потенциала Леннард-Джонса; c_s — сдвиг, обеспечивающий непрерывность потенциала на расстоянии R _cutoff . Здесь и далее в качестве единицы измерения длины берётся диаметр магнитной наночастицы, так что диаметр блоба равен 13. В этом представлении расстояние s , зависящее от типа бесструктурных элементов, составляет для двух наночастиц 2 ^{- 1/6}~ 0,891, для двух блобов ~ 0,297, а для смешанной пары 0,594. За единицу измерения энергии принимается энергия теплового движения k _B T ; для придания элементам ансамбля «твёрдости» характерное значение крутизны отталкивательного потенциала (1) устанавливается достаточно большим: s = 10.

Каждая магнитная наночастица характеризуется векторными переменными: направлением e _i , магнитным дипольным моментом ц , а также единичным вектором оси легкого намагничивания n i . Последняя необходима для того, чтобы задать одноосную магнитную анизотропию, присущую реальным наночастицам, которые используются в феррогелях. В настоящей работе рассмотрены два предельных случая указанной анизотропии, которым, по терминологии физики магнитных явлений, приписывается либо полная магнитная мягкость, либо полная магнитная твёрдость. В магнитомягкой частице дипольный момент имеет полную внутреннюю свободу вращения [8]; в магнитотвёрдой частице момент «вморожен» и может вращаться только вместе с ней как одно целое [9]. Помимо взаимодействия твёрдых сфер (при урезанном потенциале Леннард-Джонса), в выражение для энергии каждой i -й магнитной наночастицы включены: энергия взаимодействия с внешним полем H ₀ (зеемановское слагаемое), энергия одноосной магнитной анизотропии E _A [10], а также суммарное магнитное диполь-дипольное взаимодействие со всеми остальными наночастицами:

N magn

Ui”P = EL«UL (r)- це ■ H0- Ea (ei ■п. )2 +ц2 E [(e ■ eM r3"3 (ei ■ r.) (ej ■ r.) I r5 ], k, k *i где rij — межцентровой вектор частиц i и j , имеющий длину rij , N — общее число частиц в модели, Nmagn — число магнитных частиц.

Взаимодействие мономеров, связанных в цепочки, описывается посредством идентичных парных линейно-упругих потенциалов. Каждую связь можно представить как пружину заданной равновесной длины, подчиняющуюся простому закону Гука. Составленные таким образом полимерные цепочки сшиты в трёхмерную сетку, частью узлов которой являются магнитные наночастицы. Крайний мономер любой цепочки, начинающейся/оканчивающейся на данном заполненном узле, жёстко прикреплён к поверхности частицы в фиксированной точке. Вследствие этого деформация сетки МФГ происходит и при поступательных, и при вращательных движениях наночастиц. Энергия i-го «мономера» записывается в виде:

N              V

^^^^^^^

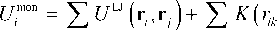
j, j * i                        k, k * i

где K — коэффициент упругости связи на растяжение/сжатие, l ₀ — равновесная длина связи, равная диаметру «мономера», v i — число соседей i -й частицы в полимерной цепочке. На длину связей наложено условие большой жёсткости ( K = 10 3 ), в соответствии с известным фактом, что энергия разрыва скелетной связи в полимере весьма высока (температура термодеструкции много выше комнатной). Однако при этом цепочка сохраняет высокую конформационную подвижность за счёт того, что энергия (2) не зависит от ориентации связи: мономеры могут свободно «кататься» друг по другу.

Элементы модели располагаются внутри ограниченной кубической расчётной области. Поскольку рассматривается уединённый объект, а не представительный объём некоторой среды, то нет необходимости в использовании периодических граничных условий. В связи с этим вычисление диполь-дипольного взаимодействия между частицами — самого трудоёмкого по временным затратам и требуемым машинным ресурсам этапа решения задачи, выполняется прямым суммированием по всем магнитным частицам.

Формирование модельного образца МФГ начинается с геометрической расстановки 10³ точек (узлов) так, чтобы они образовывали простую кубическую решётку. Узлы, занимаемые магнитными наночастицами, выбираются случайным образом в соответствии с заданным значением c — их числовой концентрацией в образце, то есть долей количества узлов, в которых будут находиться частицы; в остальные узлы помещаются мономеры (блобы). Затем все узлы соединяются между собой полимерными цепочками, содержащими равное число блобов — по 12 частиц–«мономеров», втрое меньших по диаметру, чем магнитные частицы. Все цепочки имеют одинаковую контурную длину, величина которой равняется периоду решётки. Таким образом, при выбранном типе связанности (простая кубическая решётка) каждый внутренний узел образца соединён со своими соседями в общей сложности шестью полимерными цепочками. В дальнейшем все связи типа наночастица–блоб и блоб–блоб считаются химическими, то есть неразрывными.

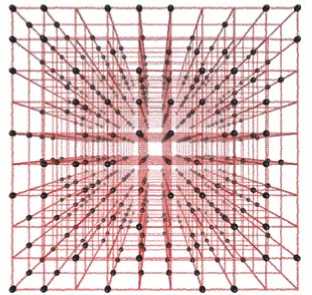
а

Рис. 1. Затравочная конфигурация, отражающая геометрию модели и связь элементов в образце ( а ); типичная начальная конфигурация, сформировавшаяся в термостате и обусловленная только стерическими взаимодействиями, межчастичные магнитные силы отсутствуют ( б ); наночастицы представлены элементами чёрного цвета, мономеры, соединённые в цепочки, – красные; доля узлов, заполненных частицами, составляет 50%

б

Когда построение «скелета» МФГ (Рис. 1а) заканчивается, очевидно, что получившаяся структура неравновесна. Тогда в компьютерную модель добавляют термостат по схеме из [11] и «включают» все межчастичные взаимодействия кроме магнитных. В этих условиях выполняется интегрирование методом Верле уравнений движения всех элементов, входящих в образец; процесс продолжается до тех пор, пока полная энергия системы не достигнет стационарной величины. Итогом этого этапа является равновесная конфигурация МФГ, имеющего заданную долю магнитных частиц (Рис. 1б). Для того чтобы снизить влияние случайных факторов (флуктуаций плотности, вызванных случайным распределением частиц по объёму образца, и стохастических колебаний температуры термостата), расчёт стационарного состояния был выполнен для 10 реализаций образца (под реализациями понимаются модели образца, отличающиеся расстановкой магнитных частиц по узлам), а затем эти реализации использовались для нахождения конфигураций с учётом магнитного взаимодействия и внешнего поля. Представленные далее результаты структурного анализа, вычисленные намагниченность и объём получены усреднением данных по этим реализациям.

Модель становится полной после включения межчастичного магнитного диполь-дипольного взаимодействия. В начале процесса вычислений частицам придаются случайные направления магнитных моментов ц i при соблюдении условия | ц i | = ц = const, то есть предположения об однодоменности частиц. Влияние этого взаимодействия на систему характеризуется безразмерным параметром, выражающим отношение энергий — магнитодипольной и тепловой — у пары частиц при их плотном контакте: Х = ц ²Д d П_р к _B T ) , где d _np — диаметр наночастицы, к _B — постоянная Больцмана, T — температура. В настоящем расчёте энергия E _A внутренней магнитной анизотропии может принимать только два значения: 0 и да , поэтому таким же будет и безразмерный параметр анизотропии: ст = E A к к _B T ; однако он удобен для обозначения предельных случаев.

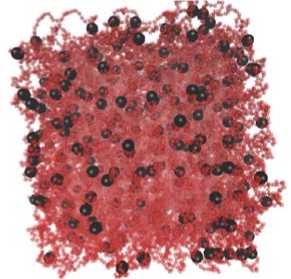
Определение равновесных конфигураций МФГ выполнялось как для случая отсутствия внешнего магнитного поля H ₀ (см. Рис. 2 а ), так и в полях конечной величины (Рис. 2 б ); напряжённость поля задавалась в безразмерной форме посредством параметра ^ = ц Я 0 /к _B T , часто называемого в литературе ланжевеновским аргументом.

а

Рис. 2. Конфигурация МФГ, полученная в результате полного расчёта с диполь-дипольным взаимодействием ( X = 5,5 ) ( а ); конфигурация, отвечающая внешнему магнитному полю § = 20 , направленному вертикально вверх ( б); магнитные частицы представлены элементами чёрного цвета, мономеры, соединённые в цепочки – красные; доля заполненных узлов 50%; для всех конфигураций ст = 0

Примеры, представленные на рисунке 2, показывают, что при достаточном уровне взаимодействия магнитные наночастицы могут отчасти преодолеть сопротивление полимерной сетки и приблизиться друг к другу. Приложенное внешнее поле усиливает эту тенденцию. В образце создаётся некоторая структура, что сказывается не только на механическом отклике образца, но и вызывает изменение его объёма. Представленные ниже результаты описывают характер образующихся структур в зависимости от концентрации частиц и их магнитных свойств.

• 3.    Структурирование под влиянием приложенного магнитного поля

  • 3.1.    Анализ цепочечных агрегатов в отсутствие внешнего магнитного поля

Равновесные конфигурации модельного МФГ были получены методом крупнозернистой молекулярной динамики с использованием программного обеспечения ESPResSo [12]. Рассматривались системы с параметрами анизотропии ст = 0 и ст = да в диапазоне значений параметра межчастичного взаимодействия X от 2,5 до 11,5 при различных концентрациях магнитного наполнителя. Величина концентрации задавалась параметром с , он, как и выше, выражает числовую долю частиц в образце.

Для измерения степени агрегирования структур из наночастиц вводится функция q(j,d): её значение отражает долю магнитных частиц, имеющих хотя бы j соседей в окрестности радиусом d [10]. Таким образом, доля частиц, находящихся в любых агрегатах, равна индикатору q(1, d), где в качестве 5 выбрана величина, близкая к диаметру наночастицы.

Результаты, представленные на рисунке 3, соответствуют значению d = 1,1 dnp. На диаграммах отчётливо прослеживается вызванный увеличением параметра X переход МФГ от неагрегированного состояния: q(1, d) — 0, к ситуации, где почти все частицы объединены в цепочечные кластеры: q(1, d) — 1.

В то же время сравнение зависимостей на рисунках 3а и 3б ясно показывает разницу в агрегировании МФГ с разной анизотропией. Как видно, для частиц, обладающих нулевой магнитной анизотропией, частицы начинают объединяться при меньших значениях параметра дипольного взаимодействия. Кроме того, переходная область в случае частиц с ст = 0 оказывается существенно уже, чем её аналог при частицах с бесконечной магнитной анизотропией.

Описанное различие обусловлено, конечно же, тем, что частицы с ст = да гораздо сильнее связаны со своим полимерным окружением. В самом деле, движущим механизмом агрегирования является выстраивание частиц в конфигурацию «голова–хвост», что отвечает состоянию с минимальной взаимной энергией (выигрыш порядка 2 X по принятой шкале). Для реализации указанного состояния магнитоизотропным частицам достаточно совершить некоторое пространственное перемещение. На этом деформация сетки прекратится, поскольку нужная взаимная ориентация магнитных моментов будет достигнута за счёт их поворотов внутри каждой из частиц. В то же время магнитотвёрдым частицам для агрегирования требуется преодолевать сопротивление сетки как при пространственных перемещениях, так и при поворотах магнитных моментов. Очевидно, что эффективное агрегирование таких частиц может реализоваться только при условии достаточно большого выигрыша в магнитостатической энергии, то есть при увеличенных значениях параметра взаимодействия X .

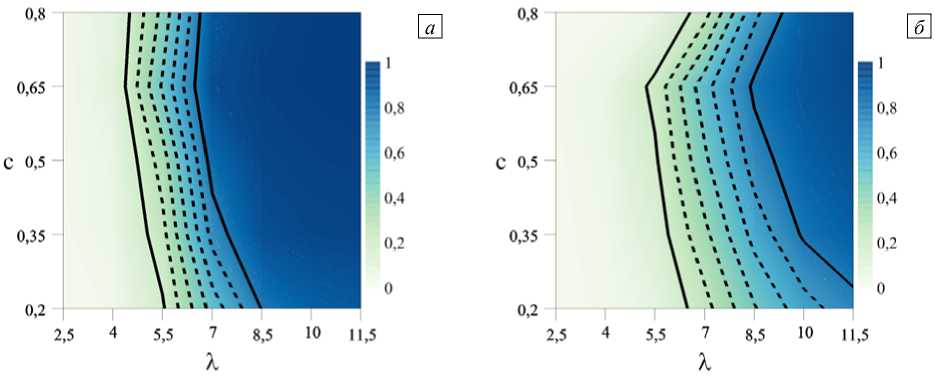
Зависимость степени агрегирования частиц q ( j , d )

Рис. 3.

при от параметра диполь-дипольного взаимодействия X и доли заполненных узлов c при магнитной

( а )

и ст = да (б); тёмные области j = 1 и d = 1,1 dnp анизотропии ст = 0

соответствуют более высокому значению степени агрегирования; сплошными кривыми изображены изолинии q = 0,2 и q = 0,8, штриховыми – изолинии для промежуточных значений

Отметим нетривиальную особенность «фазовых диаграмм» (Рис. 3). При фиксированном значении параметра взаимодействия X доля агрегированных частиц как функция концентрации ведёт себя немонотонно (см. движение по вертикали на любом из рисунков). Более отчётливо этот эффект прослеживается для МФГ с магнитотвёрдыми частицами (Рис. 3 б ). Достигнув максимума при с = 0,65, степень агрегирования затем начинает снижаться (см., например, на Рис. 3 б область вблизи с = 0,8). Иными словами, очень концентрированные феррогели менее склонны к структурной перестройке.

Общая причина такого повышения агрегативной устойчивости, на взгляд авторов настоящей статьи, заключается в следующем. Агрегирование частиц в МФГ возникает при подходящем сочетании двух основных факторов: близости взаимного расположения частиц и «полноты» воспринимаемого ими магнитодипольного притяжения. В многочастичной системе каждая частица испытывает действие полей многих соседей, но при этом создаваемые ими поля имеют очень разную величину, поскольку парный диполь-дипольный потенциал довольно быстро спадает с расстоянием. Поэтому в системе с низкой концентрацией наиболее вероятный сценарий агрегирования заключается в том, что для данной частицы случайным образом находится только один ближайший сосед, поле которого практически без помех, наводимых дальними соседями, заставляет пару сближаться. При небольшом увеличении концентрации число таких пар возрастает (поскольку среднее расстояние между частицами уменьшается), а энергетический выигрыш от объединения остаётся близким к максимальному значению 2 X . Таким образом, изменение концентрации от малых значений в сторону повышения вызывает рост степени агрегирования.

В сильно концентрированной системе среднее межчастичное расстояние невелико, и, казалось бы, агрегирование должно расти неограниченно. Однако появление многих ближайших соседей, которые окружают данную частицу по всем направлениям, приводит, в силу анизотропии магнитодипольного потенциала, к сильному экранированию их действия: локальное поле представляет собой среднее от многих знакопеременных источников и тем самым усредняется до малой величины. Иными словами, при объединении какой-либо пары выигрыш в общей энергии (как суммы большого числа знакопеременных слагаемых) оказывается незначительным. Отсюда следует, что при постоянном значении параметра взаимодействия X степень агрегирования с дальнейшим увеличением концентрации будет не расти, а снижаться.

С одной стороны, значение c = 0,65, которое соответствует воображаемым разграничительным горизонтальным линиям на рисунке 3, конечно, не является универсальным и зависит от материальных параметров конкретной изучаемой системы. С другой стороны, эффект повышения агрегативной устойчивости концентрированных МФГ, качественное объяснение которому дано выше, должен обладать достаточной степенью универсальности.

• 3.2.    Намагничивание микроферрогеля

• 3.3.    Магнитное управление объёмом микроферрогеля

Намагничивание изучалось на моделях МФГ с параметром магнитного дипольного взаимодействия Х = 5,5 и двумя близкими значениями концентрации частиц: с = 0,35 и с = 0,50, при обоих вариантах магнитной анизотропии: ст = 0 и ст = да . Указанный выбор параметра дипольного взаимодействия обусловлен следующими соображениями. Как показали предварительные численные эксперименты, при X « 5,5 агрегирование не происходит даже в образцах с высокой долей наполнителя (индикатор q (1, d ) ® 0,0). С другой стороны, при X » 5,5 система является агрегированной уже в исходном состоянии (индикатор q (1, d ) ® 1,0), поэтому при наложении внешнего поля она претерпевает лишь структурную перестройку: цепочки вытягиваются вдоль поля, вызывая тем самым некоторое увеличение объёма образца [13]. В то же время, как следует из рисунка 3, точки, представляющие образцы, выбранные для моделирования, лежат в области слабого агрегирования, но близки к переходной области. Таким образом, есть основания ожидать, что при X = 5,5 поле даже умеренной величины станет причиной интенсивного образования агрегатов, вытянутых в его направлении (см. Рис. 2 б ), иными словами, позволит эффективно управлять структурными процессами в МФГ.

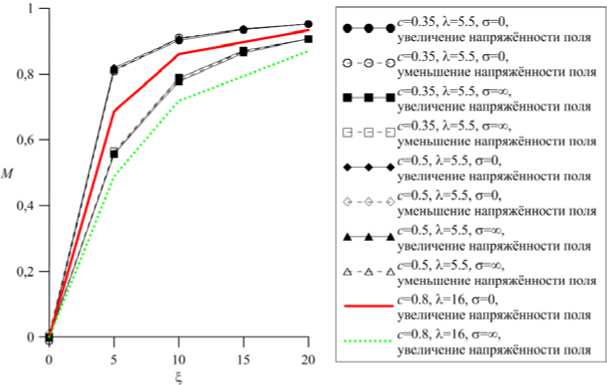
Моделирование намагничивания выполнялось путём пошагового изменения безразмерного параметра внешнего поля ^ . Для каждого следующего расчёта стартовой являлась равновесная конфигурация, к которой привело интегрирование уравнений движения всех элементов системы с предыдущим значением напряжённости приложенного поля. Параметр ^ изменялся от 0 до 20 и обратно до нуля. Результаты вычислений приведены на рисунке 4. Как видно из представленных кривых, при квазиравновесном режиме изменения поля намагниченность модельного МФГ ведёт себя обратимо: структура агрегатов соответствует данному значению напряжённости поля; в системе не наблюдается сколь-нибудь заметного количества «замёрзших» цепочечных структур, которые, однажды сформировавшись, не распадаются даже в нулевом поле. Вполне ожидаемо, что кривые намагничивания для образцов с нулевой магнитной анизотропией лежат выше графиков для микроферрогелей, содержащих частицы с ст = да . Вследствие меньших затрат энергии на деформацию сетки МФГ с такими частицами более восприимчив к намагничиванию. Для сравнения также приведены кривые для упомянутых уже высоконаполненных образцов ( с = 0,8) [13] с предельной магнитной анизотропией и сильным межчастичным взаимодействием ( Х = 16). Видно, что в этих образцах намагничивание существенно затруднено из-за наличия сформировавшейся уже в нулевом поле структуры из длинных изогнутых, пронизывающих весь образец цепочек. В этом случае выстраиванию магнитных моментов препятствуют как соседние магнитные частицы, так и взаимодействия с упругими полимерными нитями.

Рис. 4. Кривые намагничивания для выбранных конфигураций при последовательном увеличении и уменьшении величины напряжённости действующего магнитного поля; M = ( N magn H 0 )^{- 1} X ( e . ' H ) — нормированная сумма проекций магнитных моментов e _i на направление внешнего поля H ₀ , где N ^magn – количество магнитных частиц

Взаимосвязь между расположением частиц и конфигурацией сетки в МФГ приводит к зависимости эффективного объёма, занимаемого образцом, от его намагниченности, то есть, в конечном счёте, от приложенного поля. Под эффективным объёмом V понимается объём вспомогательного многогранника, построенного по следующим правилам: координаты центров всех частиц конвертируются в формат, пригодный для построения конечно-элементной сетки; затем с помощью команд программного обеспечения FEniCS [14] вычисляется объём тела, покрытого сгенерированной сеткой. Как и при расчёте намагниченности, результат вычисления объёма усредняется по 10-ти реализациям модели.

Поскольку в рассматриваемой модели МФГ и число элементов, и объём каждого из них неизменны, то эффективный объём (за вычетом суммы объёмов структурных элементов) является мерой количества растворителя, удерживаемого МФГ в равновесии. Таким образом, уменьшение/увеличение эффективного объёма при изменении напряжённости приложенного поля означает, что образец либо отдаёт, либо поглощает окружающий его растворитель. Другими словами, магнитное поле позволяет регулировать порцию растворителя, переносимую МФГ.

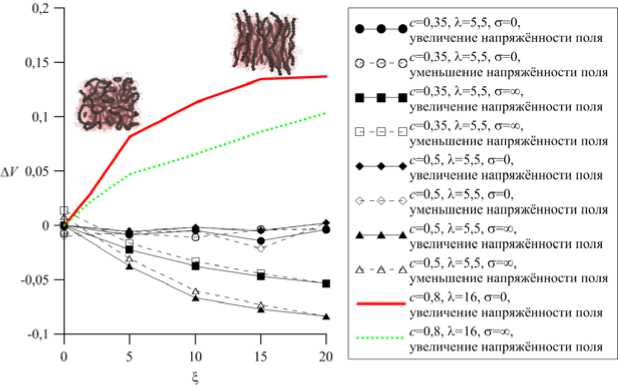
На рисунке 5 показана полевая зависимость относительного изменения объёма А V = ( V - V 0 )/ V 0 , где V 0 — объём в отсутствие поля ( ^ = 0). Как показывает структурный анализ, с ростом ^ доля агрегированных частиц увеличивается. Сближающиеся друг с другом наночастицы увлекают за собой присоединённые полимерные цепочки и тем самым сжимают сетку. Локальные уплотнения, образующиеся вокруг агрегатов, вызывают уменьшение эффективного объёма МФГ. Но при этом системы с магнитомягкими и магнитотвёрдыми частицами ведут себя по-разному.

Как показывает рисунок 5, в феррогеле с магнитомягкими частицами изменение объёма незначительно — менее 2%. В случае магнитотвёрдых частиц эффект оказывается более существенным. Так, в образце с концентрацией с = 0,5 объёмное сжатие превышает 8%. Для сравнения на рисунке 5 также приведены ранее полученные результаты для образцов с с = 0,8 и дипольным взаимодействием Х = 16. Для этих образцов основной фактор, влияющий на изменение их объёма — это перестройка изначальной «клубковой» структуры, состоящей из изогнутых агрегатов, в вытянутые вдоль поля столбцы. Микроферрогели с такой морфологией демонстрируют принципиально иной характер отклика на намагничивание. В них преобладает взаимное отталкивание цепей, что в зависимости от типа магнитной анизотропии приводит к всестороннему расширению МФГ на 10–15%.

Таким образом, можно выделить несколько типов отклика микрогеля. Для МФГ, частицы которых обладают слабым магнитным моментом, воздействие поля не приводит к агрегированию и перестройке структуры; объём образца практически не меняется. В МФГ с очень сильными диполями структура из случайно направленных цепочек образуется уже в отсутствие поля; при намагничивании эти цепочки выстраиваются вдоль направления поля. Эффект наиболее значителен при высоких концентрациях магнитной фазы, представление о такой перестройке дают вставки (картинки со структурами) на рисунке 5. Объём образца в этом случае увеличивается.

Если же намагничивать конфигурации, которые в исходном состоянии имеют малую степень агрегирования, то вызываемое сближение частиц приводит к появлению локальных сжатий сетки и, в целом, к снижению объёма образца. Эффект наиболее выражен для систем с высокоанизотропными (магнитотвёрдыми) частицами и становится всё заметнее с увеличением их концентрации.

Рис. 5. Зависимость относительного изменения объёма микроферрогеля от величины прикладываемого поля; на вставках – начальная и намагниченная конфигурации в случае высоконаполненного образца с большим параметром диполь-дипольного взаимодействия

4.    Выводы

Предложена модель, основанная на подходе крупнозернистой молекулярной динамики, явно учитывающая взаимодействие двух подсистем малого магнитополимерного объекта — магнитного микрогеля. Результаты расчётов показали значительное влияние типа магнитной анизотропии на образование цепочечных агрегатов в отсутствие поля. В рассмотренных диапазонах изменения параметров, характеризующих концентрацию частиц и их магнитный момент, представлена фазовая диаграмма, которая описывает переход к состоянию с цепочечными агрегатами. Начальные значения параметра диполь-дипольного взаимодействия, при которых начинается интенсивное агрегирование, в случаях нулевой и бесконечной магнитной анизотропии ожидаемо отличаются: повышенная анизотропия затрудняет объединение частиц.

Установлено, что доля заполненных магнитными частицами узлов полимерной матрицы оказывает заметное влияние на степень агрегирования МФГ. Как оказалось, рост содержания таких частиц (число занятых ими узлов сетки) способствует росту степени агрегирования лишь до определённого предела. По его достижению дальнейший рост числа магнитных узлов приводит к снижению агрегирования, что связано с взаимной компенсацией полей от близко расположенных соседей в месте расположения любой данной частицы.

Выполнено моделирование кривых равновесного намагничивания микроферрогелей. Обнаружено, что при невысоких значениях концентрации и параметра диполь-дипольного взаимодействия значение намагниченности, достигаемой в данном поле, существенно зависит от типа магнитной анизотропии частиц.

Показано, что эффективный объём образца МФГ изменяется под действием приложенного поля. Результат мал для случая магнитомягких частиц, но становится заметным в МФГ с магнитотвёрдыми частицами; с увеличением концентрации частиц эффект проявляется всё заметнее.

Моделирование проведено для параметров, соответствующих типичным размерам и магнитным свойствам реальных частиц наполнителей феррогелей. Так, учитывая, что значение объёмной намагниченности насыщения M s = цДл d 3 p /б ) для ферритов составляет около 400 Гс, при комнатной температуре ( k _B T « 4 - 10 - ¹⁴ эрг) получаем для Х = 2,5 и Х = 11,5, соответственно, частицы размером ~ 13 нм с магнитным моментом ~ 4,6 - 10 ^{- 16} эрг/Гс и 22 нм и магнитным моментом ~2,2 - 10 ^{- 15} эрг/Гс. При этом значения напряжённости внешнего магнитного поля при наибольшем рассмотренном значении Е = 20 для представленных параметров диполь-дипольного взаимодействия находятся в интервале ~0,4–1,7 кЭ. В зависимости от предполагаемого размера частиц поперечник образца модельного микроферрогеля составляет от 0,35 до 0,6 мкм. Исследованные концентрации, в пересчёте на объёмную долю частиц в полимерной матрице, находятся в интервале от 0,95% до 3,8%. Таким образом, эти интервалы параметров соотносятся с достижимыми в лабораторных условиях значениями, и данные, приведённые в работе, могут быть полезны как для интерпретации экспериментов, проводимых с магнитными гидрогелями с целью их биомедицинского использования, так и для предсказания свойств вновь синтезируемых микроферрогелей.

Работа выполнена при финансовой поддержке РФФИ (проекты № 17-42-590504-р_а и 18-31-00326-мол_а).