Моделирование отклонений показателей качества объекта от нормы

Ключевым понятием управления любым реальным или мыслимым объектом (Об) является его состояние [1]. В каждой предметной области задаются свои требования к состоянию управляемого Об, но общим для всех является либо сохранение состояния на заданном уровне (гомеостазис), либо его подстраивание (целенаправленное изменение) под состояние внешней среды (открытая система). Эти требования касаются как живых, так и искусственных систем, что позволяет рассматривать их с самой общей, онтологической точки зрения.

Поскольку состояние Об представляется набором значений характеризующих его показателей (параметров), целесообразно требования к описанию состояния представлять на языке задания значений показателей. На практике требования к значениям показателей формулируются на языке норм [2-4]. В прикладном смысле норме присущи следующие свойства:

• ■    любая норма относительна , ибо её устанавливает человек;

• ■    норма устанавливается теоретическим , статистическим и опытным путём;

• ■    статистическая норма - это усреднённые значения показателя, полученные при обследовании представительной группы однородных Об;

• ■    в отличие от физических и математических констант норма изменчива ;

• ■    границы нормы расплывчаты по причине усреднения значений показателя;

• ■    индивидуальные нормы отличаются от обобщённых;

• ■    профессиональные нормы отличаются от норм непрофессионалов в жёсткую сторону.

Изменчивость внутренней и внешней среды влечёт отклонение текущего значения показателя от нормы. Отслеживание отклонений показателей от нормы осуществляется в рамках мониторинга объекта. В [5] мониторинг определён как «специальная форма наблюдения (слежения) за текущим изменением тех или иных процессов или объектов в пространстве и во времени, осуществляемая на постоянной основе». Для отражения расплывчатости оценок показателей в процессе мониторинга объектов востребованы методы мягких измерений [6,7].

С точки зрения безопасности объекта различают две меры отклонения от нормы - допустимую и предельно допустимую [8, 9]. Допустимым считается процент отклонения от нормы, не оказывающий существенного влияния на функционирование Об. К предельно допустимому отклонению относится краткосрочное отклонение от нормы, не влекущее угрозы существованию Об. Выход за предельно допустимые значения показателя рассматривается как угроза существованию Об.

Недопустимое отклонение от нормы является сигналом для выработки управляющего воздействия в системе управления (СУ) Об [10]. Общность применения нормы влечёт потребность в обобщённой модели отклонений по многим показателям. Решению этой задачи посвящена настоящая статья.

1    Требования к значениям показателя

Исходя из понятия нормы, она выражается отрезком [ c _н j , c _в j ] на шкале j -го показателя, j = 1, n . Исходными данными для создания модели отклонений j -го показателя от нормы являются:

• ■    нижняя c _н j и верхняя c _в j границы интервальной нормы [ c _н j , c _в j ];

• ■    допустимые отклонения от нормы к меньшим (ДОМ) и большим (ДОБ) значениям: с _дом j ^{и с} доб j .

• ■    предельные отклонения от нормы к меньшим (ПОМ) и большим (ПОБ) значениям: с _пом j ^{и с} поб j .

Графическое представление на шкале j -го показателя интервальной нормы и отклонений от неё приведено на рисунке 1.

Норма yj cj пом        cj дом cj н        cj в cj доб      c j поб

Рисунок 1 - Графическая модель отклонений от нормы

Предельные отклонения от нормы C j _пом и C j _поб принимаются за границы шкалы j -го показателя [y j min , y j max ]: c j пом = y j min , C j поб = y j max . В общем случае допустимые и предельные отклонения в обе стороны от границ нормы не равны:

[ c j н    c j дом ^] ^ [ c j доб    c j в ^], [ ^Cj

н

c j пом

^] ^ ^[ c j поб    c j в ^] .

Выход текущего значения j -го показателя за границы шкалы модели требований к значениям показателя (y j <  y j _min или y j >  y j _max ) является сигналом для незамедлительного принятия мер. При моделировании отклонений их необходимо обнаруживать на этапе анализа исход-

ных данных.

Интервальное задание нормы можно рассматривать как интервальное ограничение показателя: y j е [ C j _н, C j _в]. Частным случаем интервального ограничения является точечная норма c j н = C j _в = C j . За точечную норму C j может быть принято среднее значение интервальной нормы C j = ( C j _н + C j _в)/2.

Принятому за норму отрезку шкалы [ y j min , C j н ] соответствует полуинтервальное ограничение сверху: y j <  C j _н (не более нижней границы), а отрезку шкалы [ C j _в, y j _max ] - ограничение снизу: y j >  C j _в (не менее верхней границы). Эти ограничения могут рассматриваться как частные случаи совпадения одной из границ интервальной нормы с границей шкалы - предельным отклонением от нормы. Ограничение «не более» C j показано в верхней части рисунка 2, а ограничение «не менее» C j - в его нижней части.

1_________________	Норма	--1            1                                  1 \
			yj
с j пом		C j    Cj доб       C j поб
		Норма
-1----------------	------------------------1--------------------------------------------	--   ч	y j
с ____ j пом	c j дом	C j               C j поб

Рисунок 2 - Модель нормы в терминах полуинтервальных ограничений

С точки зрения допустимости отклонения от нормы целесообразно различать нейтральные и оптимизируемые показатели. У нейтрального показателя отклонения значений в обе стороны от границ нормы нежелательны, а у оптимизируемого показателя отклонение значения за одну из границ нормы предпочтительно, что соответствует полуинтервальным ограничениям «не более» и «не менее».

2    Моделирование отклонения показателя качества от нормы

Направленность и величину отклонения от нормы отражает биполярная функция отклонений. Она была предложена в [11] для моделирования ограничительных критериев «не более» (≤) и «не менее» (≥). Графики соответствующих функций отклонений применительно к точечной норме показаны на рисунке 3. Переход к интервальной норме реализуется разбиением точечной нормы Cj на интервал [cнj, cвj], представляемый полочкой на оси абсцисс. Положительной полуоси функции отклонений от нормы ставится в соответствие штраф d (yj) > 0 за нарушение ограничения, а отрицательной полуоси - премия (поощрение) d (yj )<0 за пре- вышение ограничения. Значение dн(у) = 0 означает принадлежность значения j-го показателя точечной или интервальной норме.

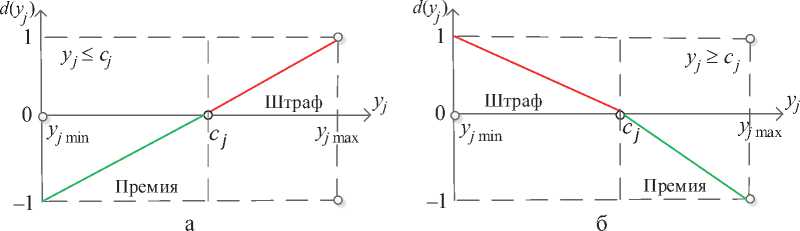
Рисунок 3 - Функции отклонения от точечной нормы: а - минимизируются; б - максимизируются

Значения кусочно-линейной функции отклонений от нормы для предиката «не более» (минимизируемый показатель) вычисляются по следующим формулам [12]:

d_ (yj) = yj cн j если yj < cн j,(1)

c н J — yj min yj-c ■ d+ (yj) =------—, если у > cв j.(2)

y j max - c в J

Значения кусочно-линейной функции отклонений от нормы для предиката «не менее» (максимизируемый показатель) вычисляются по следующим формулам:

d+(yj) = cнj yj , если yj < cнj,(3)

н j y j min d ’ (yj) = cв j yj , если yj > cв j.(4)

• v.—

• y j max     в j

• 3.1    Кусочно-линейная функция принадлежности классу

Функции отклонения от нормы применимы к оптимизируемым показателям, значения которых минимизируются (рисунок 3а) или максимизируются (рисунок 3б). Функция отклонения нейтрального показателя униполярна, поскольку отклонения в обе стороны от нормы нежелательны и оцениваются только штрафами.

3 Моделирование меры принадлежности показателя качества норме

Моделирование принадлежности норме предполагает построение соответствующей функции принадлежности (ФПр) на шкале каждого оцениваемого показателя [13]. В отсут- ствие уточняющей информации эта функция является кусочно-линейной -для интервальной нормы эта функция трапецеидальная, а для точечной нормы треугольная. У трапецеидальной функции на отрезке шкалы [cj н, cj в] принадлежность норме одинакова, а при отклонении от границ cj н и cj в в обе стороны принадлежность норме равномерно убы-

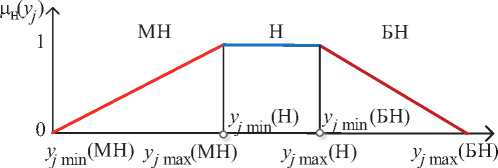
Рисунок 4 - Функция принадлежности классу «Норма»

вает (рисунок 4). Шкала значений показателя на рисунке 4 делится на три отрезка:

[y j min (MH), y j max (MH)], [ y j min (H), y j max (H)], [ y mln (БН), y j max (БН)]. Эти ОТреЗКИ ШКаЛЫ Значений показателя трактуются как «меньше нормы» (МН), «норма» (Н) и «больше нормы» (БН).

Согласно требованию раздельного анализа отклонений значений показателя по обе стороны от границ нормы модель ФПр классу Н с нечёткими границами разделим на три класса: МН, Н, БН. Значения показателя, не достигающие нижней границы нормы, относятся к классу МН, а превышающие верхнюю границу нормы - к классу БН. ФПр p k (y j ) классов Н, МН, БН строятся автоматически по признакам норм (предикатов [], < , > ).

Классифицируемый Об по значению любого показателя относится к одному из трёх классов МН, Н, БН. Принадлежность значения показателя классу МН или БН позволяет оценить направление и относительную величину его отклонения от нормы.

На рисунке 5 показана классификация значений j -го показателя на три класса. Для вычисления величины принадлежности каждому из трёх классов привлекается функция отклонений от нормы d(y j ), изображённая на рисунке 6. С учётом того, что принадлежность классу «Норма» р _н ( у ) = 1, величина принадлежности классам МН и БН вычисляется по формулам:

Если d(yj) = 0, то рн (yj) = 1;          Рмн (yj) = 0;  рбн (yj) = 0;(5)

Если d(yj) < 0, то рмн (yj) = 1 - | d(yj )|; Рн (yj) = 0;    p бн (yj) = 0;(6)

Если d(yj) > 0, то рбн (yj) = 1 - d(yj);  Рн (yj) = 0;    Рбн (yj) = 0.(7)

рД)

МН

Н

БН

y> mln (БН)

y. . (МН) y. (МН)     y.    (Н)

Jj min'    ' yj max           yj max y.   (БН)

j max

Рисунок 5 - Кусочно-линейные функции принадлежности трём классам

^{d (} y_j )

0 т----- y j min

МН

Норма

БН

c j в

y j max ^yj

Рисунок 6 - Функция отклонений от интервальной нормы

Нулевая принадлежность классу Н в формулах (6) и (7) следует из прямоугольной формы функции принадлежности и реализует закон двоичной логики, не учитывая взаимозависимости класса Н с соседними классами. Для учёта этой взаимозависимости требуется вычисление величины принадлежности классу Н как дополнения отклонения от нормы до 1. Это достигается заменой средних членов выражений (6) и (7) на формулы:

Р н (y j ) = 1 - Р мн (y j );

Р н (y j ) = ^{1 -} Р бн ⁽y j )•

Частичная принадлежность классу Н реализуется с применением нелинейных ФПр клас- су.

• 3.2    Нелинейная функция принадлежности классу

Для учёта соотношения классов МН и БН с классом Н следует использовать принцип усиления / убывания интереса лица, принимающего решения (ЛПР), к отклонению от нормы, подобного принципу склонности / несклонности ЛПР к риску [14]. В качестве уточняющей информации в модель отклонений от нормы включены допустимые отклонения от нормы к меньшим (ДОМ) и большим (ДОБ) значениям: C j _дом и C j _доб.

Ценность информации об отклонении значения показателя на отрезках шкалы [ с, н, Cj дом] [ с, в, с, доб] от границ нормы до допустимых значений j-го показателя невелика. До приближе- ния к допустимым границам отклонения от нормы принадлежность отклонениям принимается незначительной и нелинейно возрастает по мере приближения к границам шкалы с максимальным ростом в точках с, дом и с, доб. Этот принцип реализуется логистической функцией - убывающей для класса МН и возрастающей для класса БН. Моделирование классов МН и

БН соответственно убывающей и возрастающей логистическими функциями показано на рисунке 7.

Применительно к ФПр классу Н принцип реализуется в двух вариантах - полной и убывающей принадлежности норме. Он демонстрируется верхней и нижней моделями на рисунке 7. Для полной принадлежности норме сохраняется условие ц _Н( x ) = 1, x е [ с , _н, с , _в]. На областях определения [ с , _дом, с , _в] и [ с , _н, с j доб ] строятся соответственно возрастающая и убывающая параболы . Убывающая принадлежность норме описывается колоколообразной функцией с ц _Н( x ) = 1 в средней точке нормы ( с , _н + с , в )/2.

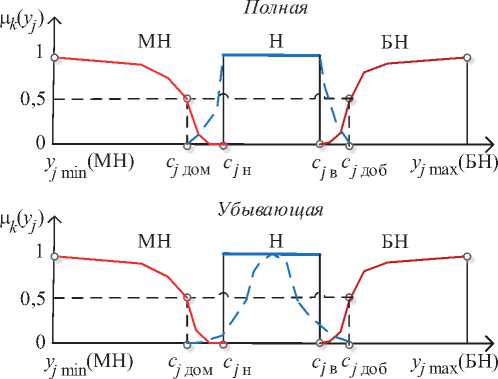
Рисунок 7 - Нелинейные функции принадлежности трём классам

4    Классификация объекта относительно нормы

При непересекающихся ФПр классам значение показателя может принадлежать только одному классу и двум классам - в противоположном случае. Принадлежность Об классу по многим показателям вычисляется как средневзвешенная функция частных принадлежностей этому классу по формуле:

n

Ц k ( x ) = £ w , • ц ,k ( x ),    k = Н, МН, БН.                       (10)

j = 1

Весовой коэффициент w , отражает важность показателя по отношению к остальным. При равенстве весов w , =1/n формула (10) сводится к среднеарифметической функции.

Для общей характеристики Об представляет интерес не только мера его принадлежности норме и классам МН и БН, но и отношения ЛПР к этим отклонениям. Для представления этого отношения вводятся два дополнительных класса «хуже нормы» (ХН) и «лучше нормы» (ЛН). Нежелательность отклонения значения нейтрального показателя в любую сторону от границ нормы выражается через делегирование принадлежностей классам МН и БН в класс ХН.

Для оптимизируемых показателей нежелательной является принадлежность только одному из этих классов. Принадлежность противоположному классу предпочтительнее принадлежности норме и имеет значение ЛН. Значения класса ЛН формируются из принадлежностей классу БН для максимизируемых показателей и из принадлежностей классу МН для минимизируемых показателей.

Принадлежность Об классам ХН и ЛН по всем показателям вычисляется также по формуле (10). Обобщённая оценка принадлежности классам Н, ЛН, ХН называется индексом класса. Согласно смыслу этих классов их оценки трактуются соответственно как индексы стабильности , развития и ухудшения свойств Об. В таблице 1 приведены примеры формирования классов ХН и ЛН на основе классов МН и БН и расчёта принадлежности Об каждому из классов применительно к кусочно-линейной модели принадлежности.

Таблица 1 – Примеры расчёта меры принадлежности объекта классам

Нейтральные показатели						Показатели min
	МН	Н	БН	ХН			МН	Н	БН		ХН	ЛН
П1	0	1	0			П4	0	1	0
П2	0,25	0,75	0	0,25		П5	0	0,5	0,5		0,5
П3	0	0,5	0,5	0,5		П6	0,25	0,75	0			0,25
						Показатели max
						П7	0	1	0
						П8	0,25	0,75	0		0,25
						П9	0	0,5	0,5			0,5
Расчёт	0,25/3	2,25/3	0,5/3	0,75/3			0,5/6	4,5/6	1,0/6		0,75/6	0,75/6
Индекс	0,083	0,75	0,167	0,25			0,083	0,75	0,167		0,125	0,125

Левая часть таблицы охватывает три возможных состояния нейтральных показателей П1-П3, а именно, принадлежность классам Н, МН и БН. Величина принадлежности норме определена как дополнение принадлежности отклонению от нормы до 1 (числа помечены курсивом). В класс ХН делегируются принадлежности классам МН и БН. В строке «Расчёт» приведены формулы вычисления среднеарифметических оценок принадлежности классам по всем равноважным показателям, а в строке «Индекс» – полученные оценки.

Правая часть таблицы охватывает по три возможных состояния оптимизируемых показателей П4-П9. В класс ХН минимизируемых показателей переносятся данные из класса БН, а для максимизируемых показателей – из класса МН. В столбец ЛН переносятся данные из противоположных классов. Жирным шрифтом в строке «Индекс» выделены индексы стабильности , ухудшения и развития Об. По нейтральным показателям индекс развития не вычисляется из-за отсутствия класса ЛН.

5    Обобщённые оценки состояния объекта

Отклонение какого-либо показателя качества Об от нормы является поводом для принятия решения по управлению его состоянием. Наряду с частными отклонениями Об от нормы представляет интерес общая оценка его состояния. Она востребована при наблюдении динамики состояния Об, а также для сопоставления его с состояниями однородных Об, что особенно актуально для сложных Об, характеризуемых десятками показателей. Эта задача может быть решена введением числового индикатора состояния (ИС) Об [15].

В качестве индикатора состояния объекта x , отражающего принадлежность норме и отклонениям от неё, примем аддитивную свёртку оценок соответствующих показателей:

ИС⁽ x ) = Е wk ■ Pr (и k ⁽ x ), c k ).                                    (ii)

k = 1

В формуле (11) сомножитель Pr ( ц k ( x ), c k ) представляет собой значение критерия, сформированного на основе показателя принадлежности объекта x k-му классу, c k и w k - целевое значение и важность этого показателя. Значениями c k являются min или max.

В решаемой задаче рассматриваются две тройки показателей принадлежности классам – с первичными и вторичными отклонениями. К первой тройке относятся показатели принадлежности классам Н, МН и БН, а ко второй - показатели принадлежности классам Н, ХН и ЛН.

В задаче мониторинга объекта используются классы Н, МН и БН. Требованию соответствия всех показателей объекта норме отвечают следующие критерии:

ц _Н( x ) ^ max, ц _МН( x ) ^ min, ц _БН( x ) ^ min. (12)

Соотношение между составляющими целостной оценки задаётся вектором весов: w = ( w ( ц _МН( x )); w ( ц _Н( x )); w ( ц _БН( x ))). Значения весов задаются в зависимости от интереса ЛПР к этим составляющим. В том случае, когда отклонения в разные стороны от границ нормы неравноценны, классы МН и БН имеют разную важность. Бо_̀льшая важность одного из двух отклонений значения показателя качества от границы нормы будет указывать на бо_̀льшую опасность ухудшения свойств Об. Учёт важности отклонений от нормы позволяет оценить тенденцию более опасного ухудшения свойств Об.

В задаче оценивания объекта с точки зрения соотношения его стабильности и развития используются классы Н, ХН и ЛН. Принадлежность классу ХН отражает степень ухудшения состояния Об, а классу ЛН - его улучшение по отношению к норме. Таким образом, качество состояния Об отражают критерии:

Ц _ХН( x ) ^ min, ц _Н( x ) ^ max, ц _ЛН( x ) ^ max. (13)

Соотношение между составляющими целостной оценки задаётся вектором весов: w = ( w ( ц _ХН( x )); w ( ц _Н( x )); w ( ц _ЛН( x ))). Значения весов задаются в зависимости от интереса ЛПР к этим составляющим. Предпочтение стабильности выражается большим весом показателя ц _Н( x ), например, w ₀ = (0,17; 0,5; 0,33), а предпочтение развитию - большим весом показателя Ц _ЛН( x ), например, w _₽ = (0,17; 0,33; 0,5).

Нейтральные показатели участвуют только в оценивании стабильности Об. Из этого следует их нулевая принадлежность классу ЛН. Она отражается и в назначении только двух весовых коэффициентов классов. Например, при равной важности классов Н и ХН вектор w с имеет следующий вид: w ₀ = (0,5; 0,5; 0). Поскольку индикатор состояния Об вычисляется по разным исходным данным для нейтральных и оптимизируемых показателей, целесообразно оценивать их раздельно.

При равной важности критериев принадлежности классам величина индикатора состояния Об зависит только от их значений, а они, в свою очередь, зависят от меры принадлежности первичных показателей норме и отклонениям от неё. Таким образом, для фиксированного набора первичных показателей и установленных для них норм индикатор состояния объекта представляет собой конкретную обобщённую характеристику состояния объекта относительно нормального состояния. Его величина равна единице в том случае, когда для тройки классов Н, МН, БН ц _МН( x ) = ц _БН( x ) = 0. Из этого условия следует ц _ХН( x ) = 0. Величина индикатора состояния играет роль потенциала объекта в отношении его стабильности и развития. Чем она ближе к единице, тем выше качество оцениваемого по этим свойствам объекта. Это даёт возможность оценивать динамику стабильности и развития объекта, а также сопоставлять его по этим свойствам с другими объектами.

6    Программная реализация задачи анализа отклонений объекта от нормы

Задача анализа отклонений Об от нормы реализована в новой редакции инструментальной системы выбора и ранжирования СВИРЬ-М, разработанной на языке Java к.т.н. доцентом Д.П. Бураковым во взаимодействии с автором. Эта задача является разновидностью многомерной классификации Об. В отличие от произвольной классификации число классов в этой задаче и их назначение фиксированы и являются производными от класса Н. По заданию границ нормы, отклонений от неё, признаков ФПр классу, типа показателя автоматически строится любая из трёх рассмотренных моделей на шкале каждого показателя, участвующего в оценивании.

Под признаками ФПр классу понимаются линейность / нелинейность её значений. Под типом показателя понимается нейтральный, минимизируемый и максимизируемый показатели. Подготовка исходных данных для решения задачи выполняется в табличном пакете MS Excel в виде таблиц «Объекты/Показатели» и «Требования к показателям».

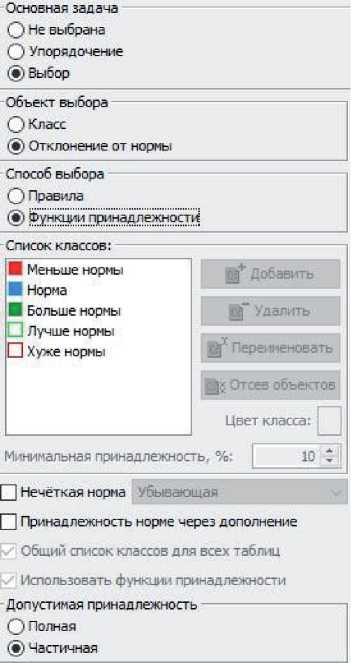
Автоматически сформированная модель для решения задачи многомерной классификации при необходимости уточняется пользователем системы средствами редактирования модели. Изменению подлежат границы классов и отклонений, параметры нелинейности нелинейной модели. Простота формирования модели задачи достигается автоматизацией построения классов на шкалах показателей на этапе ввода требований к показателям. На рисунке 8 показано разделённое на две части окно настройки параметров задачи «Отклонения от нормы» в системе СВИРЬ-М.

Левая часть окна настроена на решение одной из четырёх базовых задач аксиоматической классификации [16], а именно, на отклонение от нормы по ФПр. В окне «Список классов» приведён автоматически формируемый список пяти классов. С учётом возможных отклонений от нормы выбрана опция «Частичная принадлежность» классам.

Для оценивания меры принадлежности классам по всем показателям выбрана аддитивная обобщающая функция (правая часть рис. 8). Для вычисления индикатора состояния Об активировано «Сквозное упорядочение объектов». Принимается способ формирования класса ХН из классов МН и БН по максимальному отклонению. Весам (приоритетам) классов в специальном окне задана равная важность.

Пример результатов расчёта принадлежности классам Об 1 по трём нейтральным и шести оптимизируемым показателям показан на рисунках 9 и 10. Значения показателей П1-П9, измеренных в общей шкале [0, 10], равны (5, 3, 8, 5, 8, 3, 5, 3, 8). Границы общей для всех показателей нормы определены интервалом [4, 6]. Границы и значения показателей подобраны под реализацию принадлежностей классам в таблице 1. Требованиям нормы удовлетворяют показатели П1, П4, П7 со значением 5. Остальные показатели имеют отклонения в обе стороны от границ нормы.

На рисунке 9 приведены меры принадлежности Об 1 классам по нейтральным показателям П1, П2, П3 со значениями (5, 3, 8).

Принадлежности объекта 1 по нейтральным показателям классам совпали с расчётными величинами, приведёнными в левой части таблицы 1. Принадлежность объекта 1 классу ЛН равна нулю. Индикатор состояния объекта 1 относительно вектора важности (0,5; 0,5; 0) классов ХН и Н равен 0,5.

На рисунке 10 приведены меры принадлежности объекта 1 классам по шести оптимизируемым показателям П4-П9 со значениями (5, 8, 3, 5, 3, 8).

Принадлежности объекта 1 классам совпали с расчётными величинами, приведёнными в правой части таблицы 1. Принадлежность объекта 1 с оптимизируемыми показателями классу ЛН 0,125 > 0 отражает меру его развития. Индикатор состояния объекта 1 относительно вектора важности (0,33; 0,33; 0,33) классов ХН, Н, ЛН равен 0,58. Среднеарифметическая оценка ИС объекта 1 по всем показателям вычисляется как (0,50 + 0,58)/2 = 0, 54. Эта величина, далёкая от единицы, отражает значительные отклонения объекта 1 от нормы и от оптимальных значений показателей.

• - Способ выбора класса

О Экстремальный

@ Обобщающая функция

О Мажоритарный

Обобщающая функция принадлежности

• (•) Аддитивная

Q Мультипликативная

О Гармоническая

] Отсеивать неклассифицированные объекты

2| Учитывать важность показателей

0 Сквозное упорядочение объектов

Порядок на множестве классов:

О Общий для всех показателей

Лучший класс: Норма

@ Индивидуальный для каждого показателя

Принадлежность отклонений от нормы классу "Хуже нормы’ для нейтральных показателей:

(•) Максимальная

О Минимальная

О Средняя

• - Способ упорядочения объектов

О По лексикографическому доминированию

(•) По обобщающей функции

Приоритеты классов.

Рисунок 8 – Две части окна настройки параметров задачи «Отклонения от нормы»

Рисунок 9 – Принадлежность объекта 1 классам по трём нейтральным показателям

1\6	Меньше нормы	Норма	Больше нормы	Лучше нормы	Хуже нормы	Общая оценка
Объект 1	0.083	0.750	0.167	0.125	0.125	0.58

Рисунок 10 – Принадлежность объекта 1 классам по шести оптимизируемым показателям

Применение нелинейных ФПр норме и отклонениям от неё (см. рисунок 7) существенно влияет на результаты оценивания состояния объекта за счёт быстрого роста принадлежности отклонениям. Влияние этого свойства ФПр можно показать на рассматриваемом примере с применением функций, приведённых в нижней части рисунка 7. На рисунке 11 приведены меры принадлежности Об 1 классам по нейтральным показателям П1, П2, П3 с нелинейными ФПр классам.

На рисунке 12 приведены меры принадлежности объекта 1 классам по шести оптимизируемым показателям П4-П9 с нелинейными ФПр классам.

1\з	Меньше нормы	Норма	Больше нормы	Лучше нормы	Хуже нормы	Общая оценка
Объект 1	0.167	0.334	0.318	0.000	0.485	0.285

Рисунок 11 – Принадлежность объекта 1 классам по трём нейтральным показателям с нелинейными функциями принадлежности

Рисунок 12 – Принадлежность объекта 1 классам по шести оптимизируемым показателям с нелинейными функциями принадлежности

Применение нелинейных ФПр классам удвоило меру принадлежности объекта классам МН и БН, что повлияло на принадлежность классам ХН и ЛН, и через них – на индикаторы состояния объекта в сторону их уменьшения. Таким образом, применение нелинейных ФПр отражает большее влияние отклонений от нормы на индексы и индикатор состояния объекта.

Заключение

Проблема качества функционирования объекта носит всеобщий характер. Оценивание качества осуществляется путём контроля значений показателей, характеризующих состояние объекта, на предмет соответствия норме. Однако, с одной стороны, нормы условны, поскольку задаются человеком, а, с другой стороны, под влиянием внутренних и внешних факторов имеет место выход значений показателей за границы норм. Он может считаться как недопустимым, с точки зрения стабильности функционирования объекта, так и желательным, с точки зрения его развития.

Предложенная в работе модель ФПр норме и отклонений от неё позволяет оценить направленность и величину отклонений значений показателей от нормы. Модель строится на основе задания границ нормы – номинальных, допустимых и предельных. Номинальные и предельные границы достаточны для построения кусочно-линейной (грубой) модели отклонений от нормы. Включение в модель допустимых отклонений от нормы даёт дополнительную информацию для построения нелинейных ФПр норме и отклонений от неё, учитывающих отношение к ним ЛПР.

Предложенная модель является двухступенчатой. Модель первой ступени включает классы «Норма», «Меньше нормы», «Больше нормы». Эти классы используются для решения задач мониторинга объекта. На основе принадлежности этим классам по многим показателям вычисляется индикатор состояния объекта, по которому можно судить об общем состоянии объекта.

В модели второй ступени класс «Норма» сопоставляется с двумя фиктивными классами «Хуже нормы» и «Лучше нормы», сформированными из представителей классов «Меньше нормы» и «Больше нормы». Для их формирования используется деление показателей на нейтральные и оптимизируемые. Индикатор состояния объекта, вычисляемый на основе принадлежности классам Н, ХН, ЛН по многим показателям, позволяет судить об объекте с точки зрения стабильности и развития его свойств. По отношению к единице значение индикатора состояния объекта может рассматриваться как его потенциал для сравнения развития объекта во времени и сопоставления с другими объектами. Общность предложенной модели и возможность моделирования в различных режимах системы СВИРЬ-М определяет широкую сферу её применения.