Моделирование отсрочки поимки цели в ADT-игре с тремя защитниками

лицензии, перейдите по ссылке

Существуют различные способы защиты подвижного объекта в водной среде от мобильного атакующего, оснащенного системой самонаведения: маневр уклонения, выпуск ловушки, генерирующей пузырьки [1], использование пассивных ложных целей, отражающих гидроакустический сигнал, буксируемых постановщиков гидроакустических помех (jammer, towed decoy, towed acoustic countermeasures, false-target generator) [2, 3], активный защитник, который перехватывает атакующего (hard-kill) [3], активная ложная цель (decoy) [4–5].

В настоящей статье рассматривается случай активной защиты, в то время как основная цель уклоняется от атаки, она может выпустить три ложных цели. Ложные цели отвлекают внимание атакующего, вынуждают атакующего тратить энергоресурс на свою поимку, и позволяют тем самым основной цели уйти от перехвата атакующим в связи с исчерпанием его запаса хода (soft-kill). В таком случае взаимодействие объектов может быть математически описано как ADT-игра (Attacker–Defender–Target), "атакующий – защитник – цель" [6–11].

В [8] приводится обзор методов определения управления для каждого из игроков ADT-игры. Управление может определяться на основе как нейросетевых [8, 9], так и классических подходов. В статье [10] Рубиновичем Е. Я. задача решена геометрически – найдено управление, при котором защитник, обладающий большей маневренностью, чем цель, гарантированно перехватит атакующего на его пути движения к цели.

В работах [11–13] ADT-игры исследуются на основе подхода теории дифференциальных игр, предполагается, что защитник движется быстрее цели.

В большинстве исследований каждая из сторон "атакующий – защитник – цель" представлена одним игроком. Отметим работы [12, 13], в которых проанализирована игра в случае двух атакующих. В [14] при этом решается уравнение Риккати. В работе [15] рассмотрен случай сразу нескольких преследователей, в статье [16] исследовалась дифференциальная игра с несколькими нападающими, несколькими защитниками в случае неподвижной цели.

Настоящая работа является развитием [17], в которой рассматривалась ADT-игра в плоской постановке при использовании одного или двух защитников, движущихся медленнее цели и атакующего, на случай трех защитников.

1.    Постановка задачи

Все игроки представляют собой материальные точки. Перемещение цели и защитников рассматривается в простых движениях. В декартовой системе координат движение цели описывается соотношениями:

(x_T = v _T cos(yt), lУ т = Vt sin(YT),

(1.1)

где ( x_T ( t ) , y_T ( t )) = r _T ( t ) - координаты цели в момент времени t , при этом x_T (0) = y_T (0) = 0.

Движение защитников описывается аналогичными соотношениями:

(* Di = v_d COS(Y Di ).

(1.2)

IУ Di = Vd sin(YDi) , где i = 1..3, (xD(tt), yD(tt)) = rDitt) — координаты i -го защитника в момент времени t,

Автономный атакующий аппарат двигается с постоянной скоростью и в качестве системы самонаведения использует пропорциональную навигацию [18–20]. Его перемещение задается уравнением:

r _A (t)=v _A (t)

r(t)-r_A(t) \f‘(t)—r A (t)\ ,

(1.3)

где r _A (t) - положение атакующего в момент времени t, r(t) - положение выбранной для преследования цели. Вначале атакующий движется к центру масс всех видимых объектов, осуществляя совместное преследование, т.е. r(t) = 1 (r _T (t)+r _D1 (t) + r _D2 (t) + r _D3 (t)). Далее атакующий преследует объекты отдельно, по очереди, пока не поразит основную цель или пока у него не закончится энергоресурс, т.е. пока не наступит момент времени T ax .

Курсовой угол цели у_т полагается постоянным, углы выпуска защитников y_Di оптимизируются с целью максимизации времени перехвата цели атакующим:

T — > max. (1.4)

2.    Методы исследования

Положения цели и защитников в любой момент времени вычисляются аналитически по формулам (1.1)–(1.2). Для определения траектории атакующего необходимо интегрировать уравнение (1.3), что в работе осуществлялось численно методом Рунге–Кутты с автоматическим выбором шага. Корректность работы метода была проверена на тестовых примерах с известным ответом.

На первом этапе преследования на каждом шаге интегрирования сравнивалось расстояние l = \r _A (t) — r(t) | между атакующим и центром масс коалиции цели и защитников со всеми расстояниями между игроками коалиции l ij . В случае существования таких i,j, что l > l ij , начинался второй этап преследования, на котором атакующий переключался с преследования центра масс на поочередное преследование ближайших целей. Ближайшая цель при этом определялась на каждом шаге интегрирования, атакующий мог переключаться между ними.

На каждом шаге обоих этапов преследования определялись расстояния от атакующего до ложных целей и в случае, если оказывалось, что расстояние до i-го защитника меньше е , то атакующий распознает его как ложную цель и далее этот защитник не оказывает на него влияние, движение же самого i-го защитника в этот момент прекращается.

Оптимизируемые углы выпуска защитников y_Di перебирались на сетке их возможных значений с измельчением данной сетки в окрестности максимумов функционала (1.4), полученных при решении на более грубой сетке.

Игра заканчивалась проигрышем коалиции цели и защитников в момент времени т: ^гд (т)= г_т(т), т <  T _maх, такой что в этот момент происходит поражение цели атакующим или выигрышем коалиции по полной выработке энергоресурса атакующим в момент t = T _maх, если к этому моменту цель не была достигнута атакующим.

В случае проигрыша атакующего, вычислялось расстояние между ним и целью на момент окончания игры d ( T ), а также проводилось дальнейшее моделирование до перехвата им цели в некоторый момент T в предположении о неограниченности энергоресурса атакующего, что всегда возможно при условии v _A > v _T .

3.    Результаты численного моделирования

Моделирование проводилось для обезразмеренных значений параметров: v_D = 0.3 , v_T = 0.6, v_A = 0.9 - скорости игроков, d (0) = 10 - начальное расстояние между атакующим и целью, T_m = 30 - запас энергоресурса атакующего, е = 1 - расстояние на котором атакующий распознает защитника как ложную цель.

На рисунках 1–3 закрашенными кругами отражено положение всех игроков в момент перехода атакующего от совместного преследования к поочередному, квадратом – центр масс сигналов коалиции в этот момент времени, треугольниками – начальное положении цели, защитников и атакующего. Черной линией показана траектория движения атакующего, синей – цели, красными – защитников.

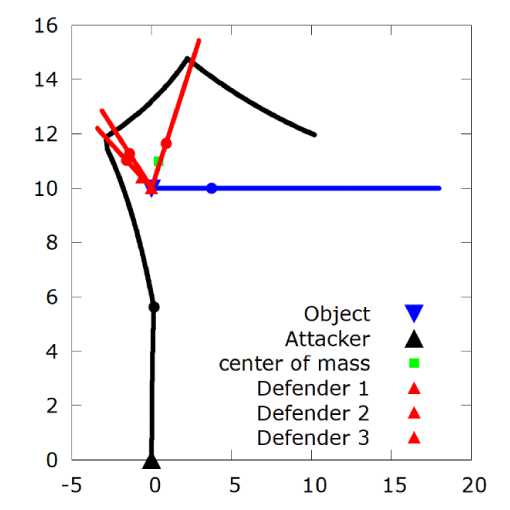
Рис. 1. Траектории движения атакующего, цели, трех защитников, соответствующие оптимальным углам выпуска защитников для курсового угла цели у_Т = 0°

В случае курсового угла цели у_т = 0 ° оптимальными углами выпуска трех защитников оказались 61.3 6°, 13 7.56° и 147.17° соответственно. При этом d ( T _maх) = 8.04 , T = 56.49, см. рис. 1.

В случае у_т = 30 ° оптимальными углами выпуска защитников оказались -133.40°, -4.3 8° и 143.41°. При этом d ( T _max) = 7.82, T = 55.78, см. рис. 2.

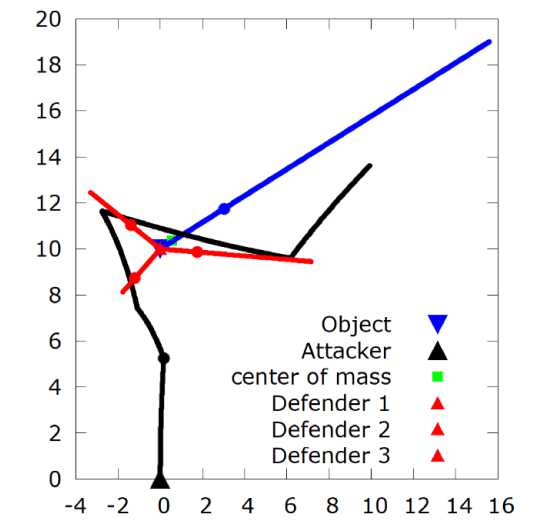
Рис. 2. Траектории движения атакующего, цели, трех защитников, соответствующие оптимальным углам выпуска защитников для курсового угла цели у_Т = 30°

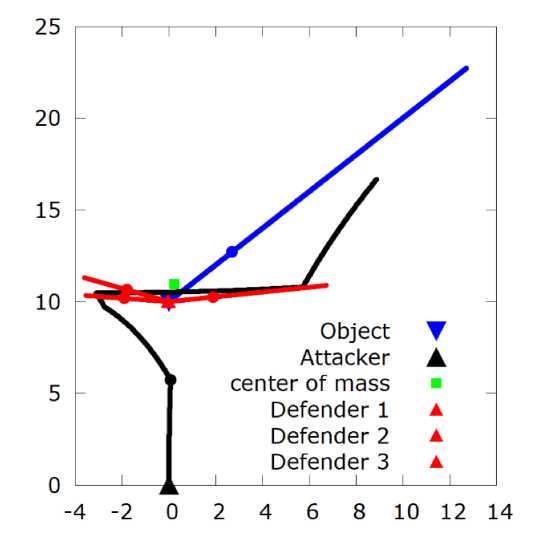
Рис. 3. Траектории движения атакующего, цели, трех защитников, соответствующие оптимальным углам выпуска защитников для курсового угла цели у_Т = 45°

В случае у_т = 45 ° оптимальными углами выпуска защитников оказались 7.47°, 160.12° и 174.65°. При этом d (T^ _х) = 7.19, T = 53.75, см. рис. 3.

Отметим, что в каждом из рассмотренных случаев атакующему хватает энергоресурса для перехвата цели в случае отсутствия защитников.

В результате проведенного численного моделирования, в котором оптимизировался выпуск защитников, во всех трех рассмотренных случаях получены сценарии выпуска защитников, при которых атакующий не сумеет догнать цель до исчерпания своего энергоресурса, что означает целесообразность выпуска ложных целей для защиты от атакующего, оснащенного системой самонаведения.

4.    Заключение

В работе рассмотрена ADT-игра пяти игроков: атакующего и коалиции из цели и трех защитников. Динамика задачи рассматривается в простых движениях, цель и защитники движутся прямолинейно. Атакующий оснащен системой самонаведения, его траектория определяется законом пропорциональной навигации.

Проведено численное моделирование для трех различных курсовых углов цели, найдены оптимальные углы выпуска защитников, позволяющие максимально отсрочить поимку цели атакующим. В каждом из случаев найдены решения для коалиции, при которых атакующий последовательно преследует ложные цели и в итоге ему не хватает энергоресурса для перехвата основной цели.

В качестве развития работы задача может быть рассмотрена в 3-мерной постановке с более сложной динамикой объектов, с ограничением на время выпуска защитников, может быть исследован вопрос оптимизации угла маневра защищаемого объекта и проанализирован случай нескольких атакующих.