Моделирование параметров бурного потока при обтекании выпуклого угла

Настоящая работа, является продолжением исследования решения плановых задач гидравлики по определению основных параметров двухмерных бурных потоков. В отличие от физической плоскости течения, в которой базовая система, уравнений движения существенно нелинейная и для которой в настоящее время аналитические решения плановых задач не известны, в плоскости годографа, скорости получена, линейная система, уравнений, на. основе которой строится широкий класс решений двухмерных плановых задач.

Задача, обтекания бурным равномерным потоком выпуклого тупого угла, рассматривалась в [1] непосредственно в физической плоскости течения потока. Двухмерная плановая задача, об обтекании выпуклого угла, решалась в [1] аналитически в предположении, что после обтекания потоком тупого угла, вдоль границы течения поток также является равномерным. “ “

Для развития метода, расчета, параметров бурного потока, с применением плоскости годографа, скорости в работе [2] этим методом была, решена, задача, о радиальном растекании бурного потока, с последующим переходом в физическую плоскость. Также была, предложена, методика, решения ряда, задач по плановому растеканию бурных потоков и была, обоснована, правомерность использования плоскости годографа, скорости.

Целью настоящей работы также является применение плоскости годографа, скорости для определения параметров бурного потока, при обтекании выпуклого угла, и сопоставление полученных результатов расчета, с результатами в [1].

Пусть бурный равномерный поток движется вдоль прямой стенки BA в точке A граница плана течения терпит излом, в этой точке стенка развернута на угол -е ₀ (рис. 1). Пусть поток, огибая угловую точку A. движется вдоль стенки AC. которая также явля ется прямой.

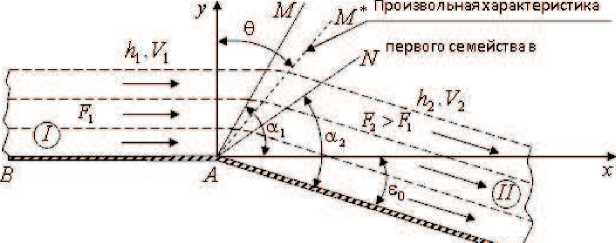
С

Рис. 1. Образование простой центрированной волны в окрестности выпуклого угла.

Считаем достоверным условием, что стенка AC является линией тока и поток вдоль стенки AC является равномерным.

Как показано в [1], границей между равномерным и неравномерным потоком всегда, служит прямолинейная характеристика, тогда, к области равномерного течения, которой в плоскости годографа, соответствует одна, точка, примыкает простая волна, т. е. простые волны служат переходной формой от равномерного потока, к неравномерному. Таким образом, два. равномерных потока, разделены простой волной. Определим границы этих потоков. Обозначим числа Фруда для каждого из равномерных потоков I и II соответственно F1 1i F 2. пусть при этом F 2 > F1. Согласно [1]. границами этих потоков являются прямые AM и AN, которые являются характеристиками первого семейства с соответствующими волновыми углами (рис. 1):

α = arcsin , α = arcsin .                          (1)

1              F1 ,     2              F2

Вдолв характеристики второго семейства, пересекающей характеристики, выходящие из тонки A. будет выполнено условие [1]

ε -  ^√3 arctg ^{r F}

-

+ arcsin

F

-

2η,

или в виде, предложенном в [3]

ε -

3 arctg

3 τ - 1

3(1 - τ )

1 + arcsin

-

τ

2τ

-

2η,

где т = FF+2' т = 2VH — квадрат скоростного коэффициента потока: е — угол, опреде ляющий направление Лектора скоростей частиц потока; H 1 — постоянная, определяемая

V ²

H = 1 +h              V h           I η величина вдоль характеристики.

Так как в потоке I выполняется е = 0. F = F 1. то

1 η=2

√3 arctg rF

-

+ arcsin

F

.

Поскольку угол е в задаче обтекания выпуклого угла изменяется от нуля до е = — Е о т. е. всегда, отрицателен, то уравнение (2) с учетом (4) примет вид:

Е* =	√3 arctg         + arcsin       -  √3 arctg    1    + arcsin        ,   (5) 3              F                   3              F 1

Е* = |Е|-

Максимальный угол поворота, при безотрывном обтекании стенки с изломом при за данной кпистнчпостп F 1 первого потока определяется из условия F 2 = то. h₂ = 0.

Е ε max

π

-

3 arctg

F 1₃-1

+ arcsin

F 1

)

Предельный угол поворота бурного потока достигается в (9), если положить поток I критическим, т. е. F 1 = 1. В таком случае

Emax = (V3 — 1) П « 1, 15 rad « 65, 88°.

Эти расчеты согласуются с результатами в [1].

Из (5) также следует, что для безотрывного обтекания потоком выпуклого тупого угла, должно выполняться условие:

ε0=f(F2)-f(F1),

где f (F ) = V3arctg л F- + arcsin —=.

3F

Зная, что в центрированной волне параметры потока, связаны условием (2) с исполь зованием (4). можно задавать F G [F1; F 2 ]. определяя соответствутощпй угол е вдоль характеристики первого семейства, т. е. на произвольной прямой AM * (рис. 1).

Угол 9 для характеристики первого семейства, отсчитываемый от оси OY (рис. 1) определяется по формуле

θ = ^π ₂ - α + ε .                                 (9)

Определив 9 ii F. можно определить и параметра! потока вдоль прямой 9 = const:

h = H1(1 — т ), V = т ^1/2 P2gH,                      (10)

где h1. V1- глубина, ii скорость равномерного потока. I

Таким образом, параметры потока, в центрированной волне полностью определены. Для построения линий тока, в центрированной волне выявим основные свойства, потока, в этой области течения. Поскольку два. равномерных потока, соединены простой центрированной волной, то в данной волне характеристики первого семейства. — прямые, они проходят через начало координат и имеют уравнения 9 = const, при этом вдоль прямолинейной характеристики параметры потока, постоянны, следовательно, в каждой точке характеристики выполняется

∂u ∂u ∂h rθ

= ,        = ,       = .

∂r ∂r ∂r

Согласно [1] система уравнений движения планового потока в полярных координатах совместно с уравнением неразрывности имеет вид:

Г,, dur , ue dur   ^u2 _                 пи^Т'"^{1 +} h )    Tur бЭТ ⁺ V dD---~ = -g ^sln Ц ^cos ° - g ^cos Ц dr-- Tr ;

< ц ^due l " » ^du6 -I- u r ue —             infl a и ^d(zo+h)     Tn-                 fl24

u r^F ⁺ VdTT ⁺~ = ^{— g sln} Ц ^sln ° ^{- g cos} Ц d(6)-- ^T 6 ;            ^{( )}

. ddr (rur h) + d6 (u6 h) = 0, где r. 9 — полярные радиус и угол жидкой частипы потока: ur. U6 — радиальная ii трансверсальная проекции вектора скорости; z0 — отметка дна русла; ц — продольный уклоп русла: g ^кореше силы тяжели.              ........

В рассматриваемой задаче имеем

Tr = Тб = 0, zo = const, ц = 0.(13)

В силу условий (И) и (13) система. (12) упрощается:

' '=

* U6 (.e + Ur) = -gdh;(14)

jur h ^{+ u} 6^dh ⁺ h uu ⁶ = 0.

Третье уравнение системы (14) выражает в полярных координатах условие неразрывности движения потока Q = 0, при этом справедлив интеграл Бернулли

U 2 + U2

H1 =        + h.                               (15)

2g

Из второго и третьего уравнений системы (14), как показано в [1], следует:

U 6 = Vgh-                                 (16)

Уравнение линии тока, в полярных координатах имеет вид [4]:

dr rdθ

u _r     u θ

τ h = Hi(1 - т), U6 = VgHi(1 - т), ur = PgHi (3т - 1), V = т1/2 V2gHT.

Перепишем уравнение (17) в виде

dr r

u r dθ u θ

= /

3т - 1

1-

τ

dθ.

Из уравнения (3) выразим

^Т-^^ Д1Я этого (3) перепишем в виде:

ε∗

- a =

V3 arctg

3т - 1

3(1 - т )

- 2п,

где е * = |е|. пли

Из (21) следует

Из равенства, (9) найдем d9:

Обозначим выражение

Тогда, из (22) и (23) следует

или

ε^∗ - α + 2η √₃

3τ - 1

= arctg _{3(1 - τ)}

√    ε∗ - α + 2η

3·tg

dθ = dε∗ - dα.

γ=

ε^∗ - α + 2η √₃

3τ - 1

1-τ.

dε∗ - dα   dθ dγ =       =

dθ = √3dγ .

Учитывая формулы (22), (24) и (25), уравнение (19) представим в форме

dr r

= 3tgγdγ.

Интегрируя уравнение (26), получим:

r ln = ln r0

cos3 γ0 cos3 γ

При этом, если начальную точку траектории выбрать на луче AM, то Y0

- α 1 +2 η √₃

• а, если - на. луне AN. то Y 0 = ~ТТ^'

Потенцирование (27) приводит к уравнению з cos3 γ0 r=r0 cos3 γ .

Из (28) следует, что линии тока, в простой центрированной волне являются подобными кривыми, расстояния между которыми при F2 > F > 1 увеличиваются вниз по течению потока. ”

Таким образом, поставленная в работе задача, по определению параметров потока, при обтекании выпуклого тупого угла, решена, методом использования плоскости годографа, скорости. При этом результаты, полученные в работе, совпадают с результатами в [1], где был предложен аналитический метод расчета, параметров потока, непосредственно в физической плоскости — в плане течения потока.