Моделирование перестройки трабекулярной костной ткани в ветви нижней челюсти человека

Нижняя челюсть является непарной и единственной подвижной костью лицевого скелета; к ней прикрепляется большое количество мышц, приводящих ее в движение. Эта особенность определяет сложность строения нижней челюсти и ее влияние на развитие лицевого скелета и покрывающих скелет мягких тканей [1].

Няшин Юрий Иванович, д.т.н., профессор кафедры теоретической механики и биомеханики, Пермь

В течение жизни форма и структура нижней челюсти человека претерпевают значительные изменения [10], что во многом обусловлено влиянием на нее возрастающей с момента рождения нагрузки: изначально под давлением процесса сосания, а с прорезыванием зубов – акта жевания [1]. По мере роста структура внутреннего пористого слоя кости (трабекулярная костная ткань) изменяется в соответствии с возникающим напряженным состоянием (рис. 1). Экспериментально показано, что структурные единицы трабекулярной кости – трабекулы ‒ выстраиваются вдоль линий главных напряжений, т.е. вдоль главных направлений тензора напряжений, и образуют арочную архитектуру в ветви нижней челюсти [1, 6, 9]. Данное утверждение согласуется с законом Вольфа, согласно которому трабекулярная кость в локальной области структурно приспосабливается к местному напряженному состоянию.

Помимо роста, такие факторы, как, например, возникающие патологии, приводят к изменению давления и, следовательно, перестройке костной ткани.

Решение задачи с использованием кинетических уравнений в трехмерной постановке достаточно сложно из-за большого количества обрабатываемых данных [3–6] и подробно рассмотрено только для случая перестройки бесконечно малого объема, вызванной сжимающей нагрузкой, растяжением и изгибом консоли в состоянии гомеостаза. Заложенная природой симметрия в теле человека позволяет перейти от 3 D- к 2 D- постановке и рассмотреть перестройку нижней челюсти в сагиттальной плоскости.

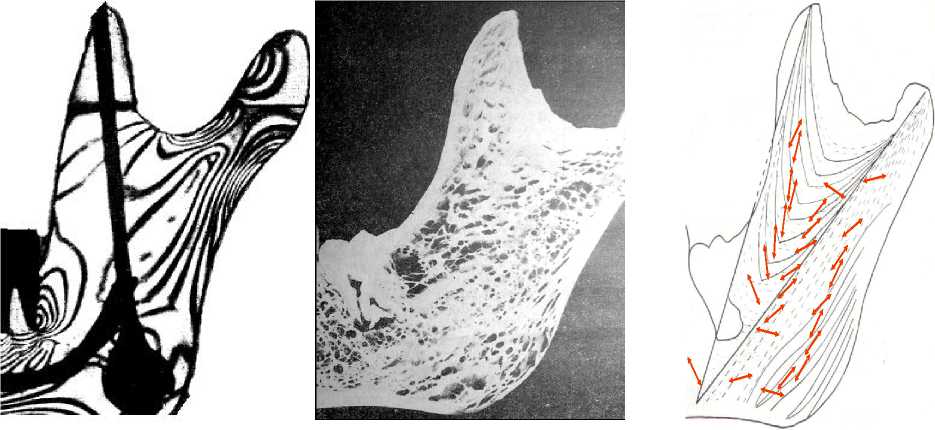
а                               б                              в

Рис. 1. Ветвь нижней челюсти. Траектории напряжения, полученные методом фотоупругости [6] ( а ), трабекулярная структура ветви нижней челюсти [1] ( б ), траектории ветви нижней челюсти и главные направления тензора структуры [10] ( в )

Постановка задачи

Нормальное функционирование кости без разрушения осуществляется в малом диапазоне деформаций, поэтому физические и геометрические соотношения, содержащие в себе зависимость от тензора деформации, линейны. Биологические ткани являются многофазными и анизотропными [10], поэтому необходимо отразить различие свойств материала в направлениях рассматриваемой координатной системы.

Из вышесказанного следует, что математическая постановка представляет собой линейную задачу теории упругости анизотропного тела, дополненную кинетическими уравнениями, описывающими эволюцию костной ткани (подробнее в статье [6]).

Концептуально задачу можно описать в следующем виде: для элементарного объема dV трабекулярной костной ткани задана начальная структура, описываемая девиатором тензора структуры K 0 и величиной, описывающей изменение доли твердого объема e ⁰ . При приложенной нагрузке P ⁰ в данном объеме возникают напряжения с тензором 6 0 и деформация с тензором в 0 . Собственные значения деформации E_t , при i = 1...3 не выходят за рамки диапазона, характеризуемого В₄ *, при котором отсутствует перестройка ( lazy zone ). В момент времени t ⁰ на тело начинает действовать добавочная нагрузка Д Р , такая что Р = Р ⁰ + Д Р , а новое значение деформации в выходит из lazy zone . Это вызовет адаптацию структуры и изменение доли твердого объема к соответствующему напряженному состоянию б .

Для сравнения тензорных величин используют их главные значения [12]. Известно [6, 12], что согласно закону Вольфа ( Wolff’s law ) окончание перестройки происходит при соосности тензоров K, 5, £ . Углы между главными направлениями K и 6 , обозначаемые через a, i = 1...3, при окончании перестройки стремятся к нулю. Необходимым и достаточным условием соосности тензоров второго ранга является коммутативность их скалярного произведения, т.е. K ■ 5 = 5 • K [2]. Деформированное состояние меняется в процессе перестройки за счет изменения K и e при неизменном напряженном состоянии. Из литературы известно, что среднее время окончания перестройки трабекулярной костной ткани человека при неизменном нагружении составляет T « 160 дней [6, 10, 12]. Для состояния всестороннего сжатия собственные значения тензора деформации E_t = 0,003 [12]. Описанную концепцию удобно представить в виде таблицы.

В качестве исходных данных для решения задачи в ANSYS Mechanical заданы величины, представленные в таблице.

В данной задаче силы, действующие на кость от мышц нижней челюсти, приложены в точках, хотя, вообще говоря, места крепления мышц образуют поверхность (рис. 2, 3).

Характеристика этапов эволюциии трабекулярной костной ткани

Этап эволюции	Гомеостаз	Начало перестройки	Процесс перестройки	Новое состояние гомеостаза
Численная характеристика	1В0  у0  с0  «г0  Р( , e , £ , о , p	K 0 , e °, £, 5, Р	K i , e i , в i, 5i , P , а i	T OT CT , e , £ , 5 , p
Условие состояния	K ■ б = 5 ■ K а,. ^ 0, i = 1..3	E i >  E * i , i = 1...3	E i > E * , i = 1...3	K ■ <5 = <5 ■ IC а, ^ 0, i = 1..3
Временной период/момент	t <  0	t = 0	0 <  t <  T , i = 1..160	t = T

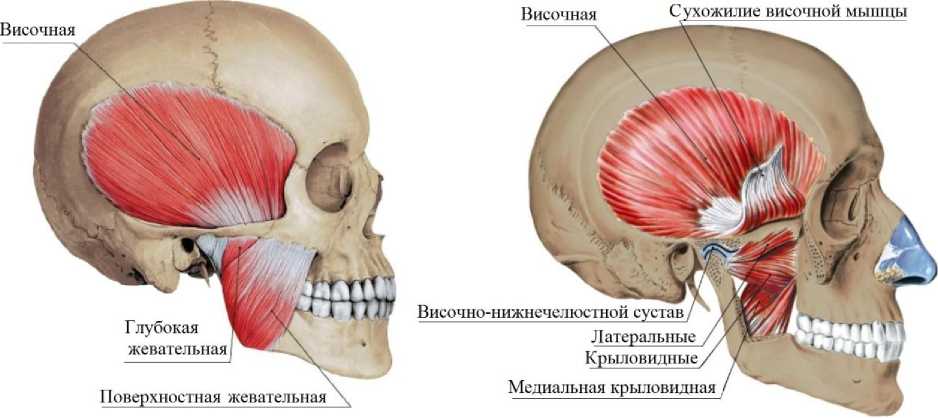
а

б

Рис. 2. Жевательные и височная мышцы, вид справа: без удаления венечного отростка и скуловой кости ( а ), с их удалением и приподнятым лоскутом височной мышцы ( б )

Напряженное состояние

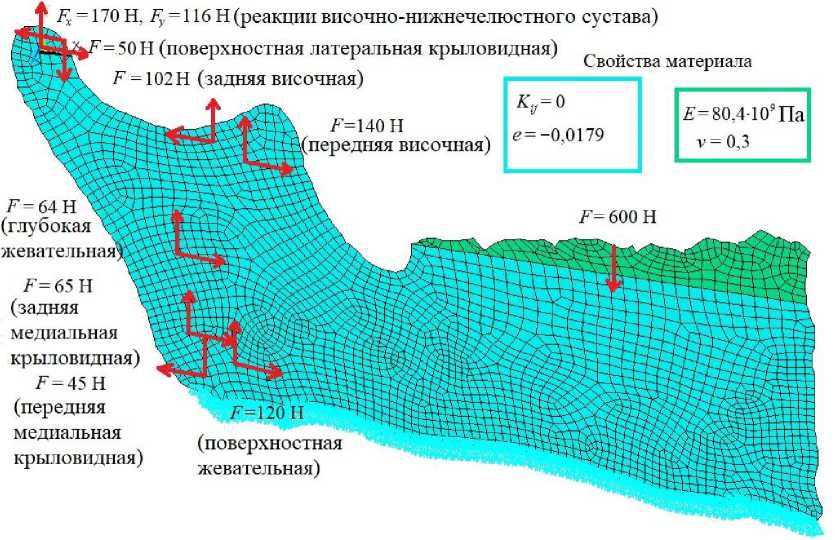
Расчет напряженно-деформированного состояния производился с помощью метода конечных элементов в ANSYS Mechanical (см. рис. 3).

Для задания конечно-элементной сетки использовался двумерный конечный элемент Plane182 , поддерживающий задание анизотропных свойств. Численное интегрирование кинетических уравнений осуществлялось методом Рунге – Кутта четвертого порядка.

материала

£= 80,410s Па v = 0,3

>=120 Н (поверхностная жевательная)

F=64H (глубокая > жевательная'

^=65Н (задняя " медиальная крыловидная)

У=45Н (передняя медиальная крыловидная)

F= 600 Н

А' =0

е=-0,0179

А=140Н ((передняя височная)

F_x = 170 Н, F_y = 116 Н (реакции височно-нижнечелюстного сустава) 3^F= 50 Н (поверхностная латеральная крыловидная) „

F = 102Н (задняя височная)

Рис. 3. Конечно-элементная постановка. Координаты мест прикрепления жевательных мышц и нагрузка от их действия на кость взяты из работы [9], силы разложены по осям

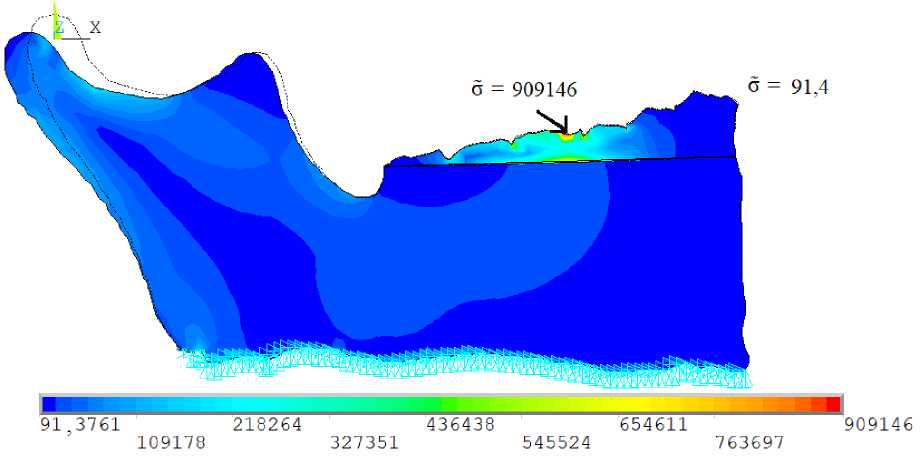
Рассмотрим картину распределения интенсивности напряжений в момент начала эволюции в двух случаях: без учета зубного ряда, при этом нагрузка прикладывается непосредственно к кости челюсти между предполагаемым нахождением второго и первого премоляра, непосредственно к зубам с изотропными свойствами ( E = 80,4 - 10⁹, v = 0,3) (рис. 4). В первом случае концентратором напряжений выступает участок между зубами, к которым приложена сосредоточенная сила, а арочное распределение напряжений в ветви нижней челюсти одинаково в обоих случаях.

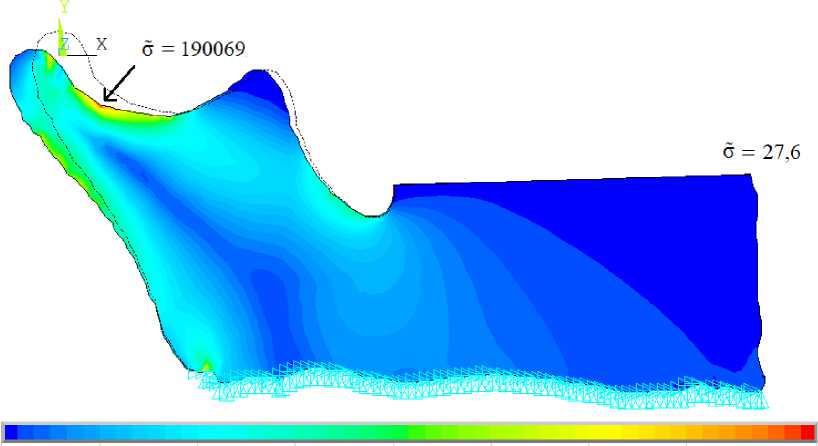
27,6066         45637,5          91247,5         136857             190069

22832,6          68442,5          114052           159662

а

б

Рис. 4. Интенсивность напряжений по Мизесу: а ‒ без учета зубного ряда; б ‒ с учетом зубного ряда

Еще одним наглядным и удобным для последующих вычислений способов иллюстрации напряженного состояния является изображение главных направлений тензора напряжений, которые показывают, как ориентированы трабекулы внутри костной ткани (рис. 5).

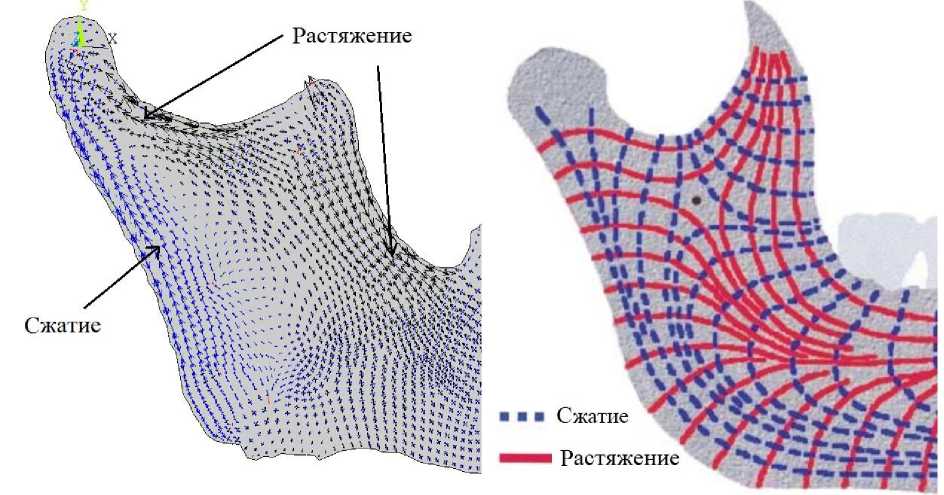
а

б

Рис. 5. Упрощенное представление распределения напряжений: главные направления, подсчитанные в ANSYS ( а ), траектории, в среднем наблюдаемые в челюсти [12] ( б )

Далее имитируется начало перестройки путем увеличения нагрузки без изменения ее вида и направления. Полученные после решения задачи компоненты тензора напряжений и деформации всех узлов геометрии импортируются в более подходящую для дальнейшего решения программу MATLAB в виде таблиц (подробнее в статье Горожениновой [4]). Моделирование следующих этапов перестройки происходит путем интегрирования эволюционных соотношений [3, 4].

Распределение пористости

Полученная по окончании перестройки кости пористость считается для каждого узла конечно-элементной сетки по формуле v = e + v (см. рис. 5) [6], где v – начальная пористость, затем v нормируется [4].

Учитывая, что красные зоны отвечают за зоны наибольшей пористости и синие, соответственно, за зоны наименьшей пористости, получим картину распределения пористости в нижней челюсти (рис. 6).

Предположение, что вся нижняя челюсть, включая зубы, состоит из трабекулярной костной ткани, на самом деле является упрощением. На рис. 6 и на рис. 1, б наблюдается некоторое сходство в распределении пористости: места прикрепления мышц являются слабопористыми участками, а середина ветви – сильнопористая. В процессе перестройки, вызванной увеличением нагрузки на зуб, происходит увеличение сильнопористой зоны и смещение ее в центр челюсти, при этом по внешним краям остается плотная костная ткань (рис. 7).

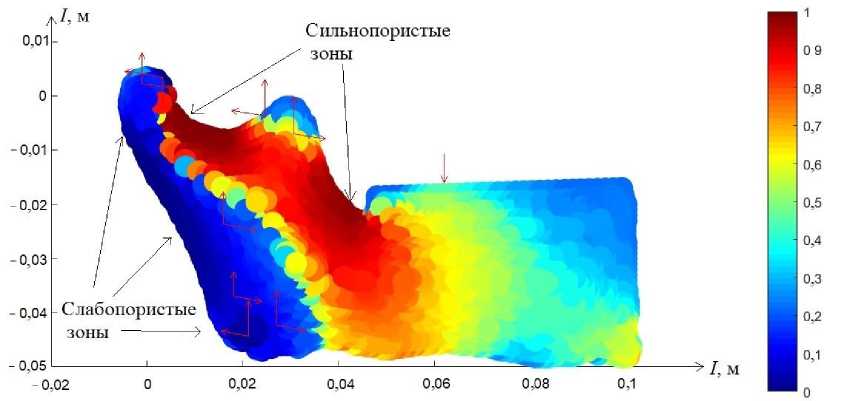
Рис. 6. Распределение пористости при t <  100 сут

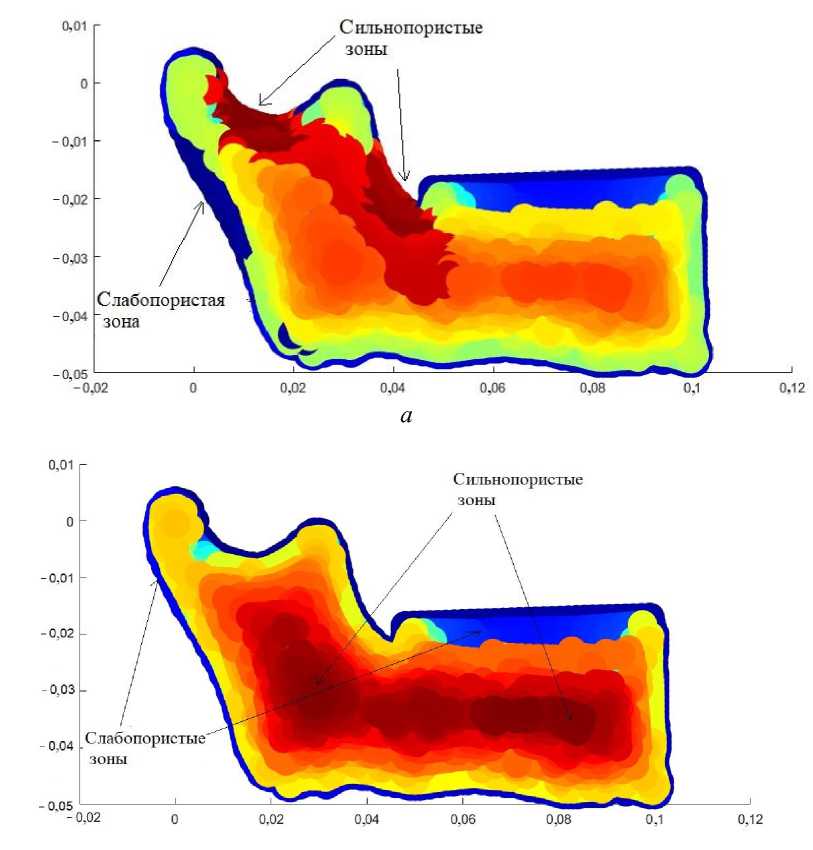
б

Рис. 7. Распределение пористости при: a - t = 120 сут, б - t = 160 сут

Результаты распределения пористости, полученные для геометрии челюсти с зубами и без них, при рассматриваемых условиях нагружения качественно совпадают.

Заключение

Рассмотрена модель перестройки трабекулярной костной ткани в ветви нижней челюсти, реализованная с помощью метода конечных элементов, с учетом кинетических уравнений феноменологической теории [12], описывающих изменения трабекулярной архитектуры на мезоуровне с помощью тензора структуры. Показаны результаты изменения пористости в течение периода адаптации и по его окончании. Рассчитанные изолинии напряжений в ветви нижней челюсти (см. рис. 4) достаточно схожи с траекториями напряжений, полученными методом фотоупругости (см. рис. 1, а ). На рис. 6 и в сравнении с рис. 1, б видно сходство в распределении пористости.

Благодарности

Работа поддержана грантом Российского фонда фундаментальных исследований № 18-01-00589_а.