Моделирование полных покрытий отрезка на основе сумм элементов плоских сечений пирамиды Паскаля

В последние десятилетия неуклонно растет число математических комбинаторных объектов и их разнообразие, что связано с решением задач моделирования и исследования различных явлений и процессов в вопросах обработки и хранения данных, анализе данных, создании алгоритмов и оптимизации. Уникальная «The on-line encyclopedia of integer sequences» (OEIS) [8], основанная Нилом Слоуном в 1964 г., содержит в настоящее время более 350 000 статей по числовым последовательностям, встречающимся в комбинаторике, теории графов и т. д. [1] Единым подходом для получения и изучения таких объектов является рассмотрение их как многоуровневых систем или систем с иерархической структурой [4, 5].

Для моделирования ряда числовых последовательностей, описываемых в OEIS, в [2] было введено понятие обобщенной пирамиды Паскаля, которую в 1993 г. предложил О. В. Кузьмин. В данной работе рассматриваются число полных покрытий отрезка и его взаимосвязь с суммой элементов плоского сечения пирамиды Паскаля. Определяются числа полных покрытий отрезка, рекуррентные соотношения и производящие функции, которым удовлетворяют эти числа. В качестве примеров приведены известные числовые последовательности.

• 1    Полные покрытия отрезка

Рассмотрим покрытия отрезка длины m тремя отрезками, длины которых равны m i , m 2 и m 3 , учитывая при этом, что m i < m 2 < m 3 , m, m i , m 2 , m 3 Е N = {1, 2, 3,...} (рис. 1). Отрезки полностью покрывают рассматриваемый отрезок, перекрывая его и друг друга только в граничных точках. Если длины двух или всех трех покрывающих отрезков совпадают, то есть m i = m 2 и/или m i = m 3 и/или m 2 = m 3 , то соответствующие совпадающие по длине покрывающие отрезки полагаем разных цветов (рис. 2), при этом граничные точки всех отрезков для определенности оставляем бесцветными. Два покрытия считаем различными, если они отличаются либо составом покрывающих элементов, либо порядком их расположения. Такие покрытия назовем полными (m; m i , m 2 , m 3 )-покрытиями.

Обозначим через µ наибольший общий делитель чисел m 1 , m 2 и m 3 :

ц = НОД (mi, m2, m3) , тогда возможны два случая:

• 1)    если m = цк, к Е N , то число полных (m; m i , m 2 , m з )-покрытий совпадает с числом полных (к; m 1 /ц,m 2 /ц,m з /ц)-покрытий;

• 2)    в противном случае, если m = цк, к Е N , то не найдется ни одного полного (m; m _i , m 2 , m з )-покрытия.

Поэтому в дальнейшем, не умаляя общности рассматриваемых случаев, положим

НОД (m i , m 2 , m 3 ) = 1

и найдем число полных покрытий отрезка.

Рис.

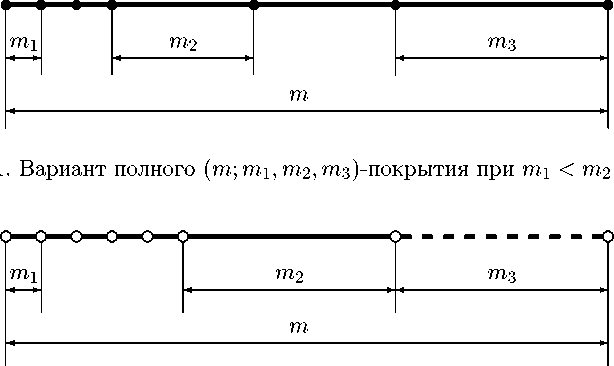
< m 3

Рис. 2. Вариант полного (m; m i , m 2 , m з )-покрытия при m i < m 2 = m 3

2 Плоские сечения пирамиды Паскаля

Пирамидой Паскаля называем бесконечную иерархическую трехгранную пирамидальную структуру, элементы которой для целых неотрицательных n, k, l удовлетворяют рекуррентным соотношениям:

n + 1 k, l

n

к —

1,1

+

n

k, l - 1

+

n

k, l

с граничными условиями:

(°°°) = 1; (knj = 0, если min(n, k,l,n — к — l) < 0, где (knz) = k! l! (n— k-Г)'. — триномиальные коэффициенты, для которых справедливы равенства:

n

k, l

n

0, 0

n n, 0

n

0, n

= 1,

n

n

n

l, k

n

— к — l,l

к, n — к — l

что свидетельствует о наличии трех осей симметрии в пирамиде Паскаля [2].

Для решения поставленной задачи будем рассматривать пирамиду Паскаля в прямоугольной декартовой системе координат в пространстве, при этом вершину пирамиды совместим с точкой (0; 0; 0), числа n расположим по оси абсцисс, k — по оси ординат, l — по оси аппликат. Таким образом, все элементы пирамиды Паскаля однозначно совмещаются с точками (n; k; 1) целочисленной решетки первого октанта, имеющими неотрицательные координаты и ограниченными плоскостями k = 0, n = 0 и n — k — 1 = 0.

Рассмотрим треугольное плоское сечение пирамиды Паскаля, образующее углы φ 1 и φ 2 с осями ординат и аппликат соответственно. Уравнение такого сечения имеет вид [7]:

n + tg ф 1 • k + tg ф ₂ • 1 = const. (1)

Нумеруем, начиная от вершины пирамиды Паскаля, все параллельные между собой сечения, заданные уравнением вида (1), и рассматриваем последовательность сумм элементов таких сечений:

{ S n (tg Ф 1 , tg Ф 2 )} ,N E N o = {0,1,2,3,...}.

Пусть tg фг = Pr/qr,Pr E Z,qr E N, НОД (pr,qr) = 1,r = 1, 2.

В случае p r /q r > — 1 треугольник сечения конечен, и уравнение N -го плоского сечения пирамиды Паскаля принимает вид [3]:

p 1       p 2           N

q i        q 2       НОК (q i ,q 2 ) ^.

Обозначим через q наименьшее общее кратное чисел q 1 и q 2 :

q = НОК (q i ,q 2 ).

Теорема 1. Сумма элементов N -го плоского сечения пирамиды Паскаля задается формулой:

S N

p 1 p 2 q 1 ^, q 2

h q i N i h    q ₂ N    i -i

L q ( p i+ q i)J [q ( P 2+ q 2)J

E i =0

E j =0

N _ Eli _ Eli q qii q2j i, j

.

Доказательство.

N   p 1     p 2

- i- j qq q

Действительно, все элементы вида q   q1   q2    содержатся в i, j плоскости N-го сечения пирамиды Паскаля, заданного уравнением (2), поскольку

N

q

i q i

Р2 Л , Pi . , P2    . N

—j +--- i +---j = —

q

для любых целых неотрицательных i и j , являющихся соответственно ординатами и аппликатами элементов пирамиды Паскаля. Других элементов пирамиды в этой плоскости нет, рассмотрены все возможные значения i и j для узлов целочисленной решетки первого октанта.

Ограничения пирамиды Паскаля k = 0, n = 0 и n — k — l = 0 определяют вершины треугольника сечения, а именно элементы

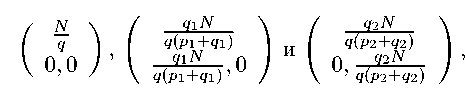
которые задают верхние и нижние пределы суммирования. Таким образом, получаем формулу (3) для вычисления суммы элементов N -го плоского сечения пирамиды Паскаля. Теорема доказана.

3 Число полных покрытий отрезка

Для нахождения числа полных (m; m i ,m 2 ,т з )-покрытий введем в рассмотрение сумму элементов m-го плоского сечения пирамиды Паскаля следующего вида:

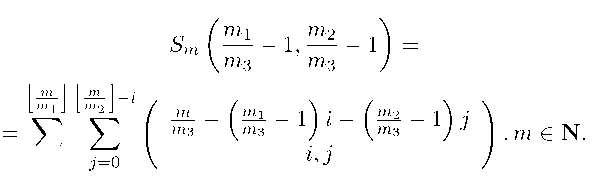
m mm

Теорема 2. Число всех полных (m; m i , m 2 , m 3 )-покрытий равно сумме (4) элементов m-го плоского сечения пирамиды Паскаля.

Доказательство.

Пусть xi,j — число полных (m; mi, m2, mз)-покрытий, составленных из i отрезков длины mi, j отрезков длины m2 и (m — mii — m2])/m3 отрезков длины m3 соответственно. Тогда число всех возможных полных (m; mi, m2, mз)-покрытий равно mm m1 m2

i =0 j =0

О. В. Кузьмин, М. В. Стрихарь. Моделирование полных покрытий отрезка на основе сумм элементов плоских сечений пирамиды ...

Так как всего покрывающих отрезков i + j +

m     m 1         m 2

следовательно m - m1i - m2j m3

----1 i ----1 j, m3   m3         m3

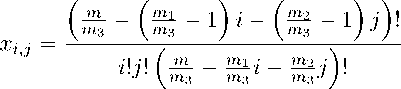
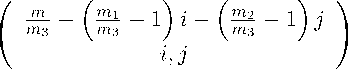
Поэтому число всех полных

h m i h m i-i m1 m2 X X i=0   j=0

(m; m i , m 2 , т з )-покрытий равно

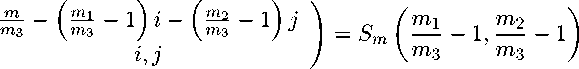
что и требовалось доказать.

Замечание. Рассмотрим случай полного (m; m i , m 2 , m з )-покрытия при m — 0. Для любых натуральных значений m i , m 2 и m 3 , при условии, что m 1 ≤ m 2 ≤ m 3 , имеем

Это число соответствует вершине пирамиды Паскаля и будет играть большую роль в нахождении рекуррентных соотношений и формальной производящей функции для числа полных покрытий отрезка. Поэтому далее берем значения m из множества неотрицательных целых чисел, то есть считаем, что m ∈ N 0 .

4 Рекуррентные соотношения

Обозначим S _m — S _m (m 1 — 1, m 2 — 1) и рассмотрим последовательность {S _m }, m Е N o полных (m; m i , m 2 , m з )-покрытий.

Теорема 3. Последовательности чисел {Sm}, m ∈ N, удовлетво- ряет рекуррентному соотношению

S m — Sm-m i ⁺ S m-m 2

⁺ S m-m 3

с начальными условиями

S i — S 2 — ... — S m i - i — 0;                     (7)

S m , при m = m i , ...,m _m 2 - i задаются соотношениями

S m — Sm-m i ^;

S m , при m — m 2 , ...,m _m 3 - i задаются соотношениями

S m

S m-m 1

⁺ S m-m 2 .

Доказательство.

Действительно, при m ≥ m 3 имеются три возможности полного (m; m i , m 2 , m з )-покрытия. В первом случае сначала произведем полное (m — m i ; m i , m 2 , m з )-покрытие, а затем добавим справа отрезок длины m i . Во втором случае сначала выполним полное (m — m 2 ; m i , m 2 , m a )-покрытие, а затем добавим справа отрезок длины m 2 . В третьем случае сначала осуществим полное (m — m 3 ; m i , m 2 , m з )-покрытие, а затем добавим справа отрезок длины m 3 . Указанные возможности образуют рекуррентное соотношение (6). В случае m — m 3 приходим к соотношению (5).

Если 1 <  m < m i — 1, то нет ни одного полного (m; m i ,m 2 ,m 3 )-покрытия, что доказывает начальные условия (7).

Если m i <  m < m 2 — 1, то число полных (m; m i , m 2 , m з )-покрытий совпадает с числом полных (m — m i ; m i , m 2 , m з )-покрытий. Получаем соотношение (8). При m — m i снова приходим к соотношению (5).

Если m 2 < m < m 3 — 1, то можно произвести полное (m; m i , m 2 , m 3 )-покрытие только отрезками длины m 1 и m 2 . Имеется только две возможности сделать это. В первом случае сначала произведем полное (m — m i ; m i , m 2 , m з )-покрытие, а затем добавим справа отрезок длины m i . Во втором случае сначала осуществим полное (m — m 2 ; m i , m 2 , m 3 )-покрытие, а затем добавим справа отрезок длины m 2 . Указанные возможности образуют формулу (9). В случае m — m 2 получаем (5).

Теорема доказана.

В силу симметрии пирамиды Паскаля из Теоремы 3 имеем:

Следствие. Для натуральных чисел m 1 , m 2 и m 3 , m 1 ≤ m 2 ≤ m 3 , НОД (m i , m 2 , m 3 ) — 1 справедливы равенства:

S m	m i — 1. m 2 — 1   =  S™ m — 1. m i — 1    = m 3     , m 3               m m 3     , m 3
= S m	( m i — 1, m 3 — 1 )   = Sm ( m 3 — 1, m i — 1 )    =     (10) m 2     , m 2               m m 2     , m 2
= S m	( m i — 1, m i — 1 )   =  S m ( m i — 1, m i — 1 ) .

5 Производящая функция

Сопоставим последовательности {S _m }, m ∈ N 0 формальный степенной ряд и найдем производящую функцию.

О. В. Кузьмин, М. В. Стрихарь. Моделирование полных покрытий отрезка на основе сумм элементов плоских сечений пирамиды ...

Теорема 4. Производящая функция последовательности сумм {Sm}, m Е No, имеет вид:

F s (x) =

1 - x m i

- x m 2 - x m a

Доказательство. Согласно Теореме 3 последовательность сумм {S m }, m Е N o , удовлетворяет соотношениям (6) — (9).

Перепишем рекуррентное соотношение (6) в виде

^S m + m a — ^S m + m a -m i + ^S m + m a -m 2 + ^S m ^.

Умножая последнее соотношение почленно на x m + ma и суммируя по m в пределах от нуля до бесконечности, получаем

∞∞

ЕС    ™ m+ma _ mi X^ с        m+ma-mi , m+max     — x /  °m+ma-mix        +

∞∞

+x ^m 2 X S m + m a -m 2 x m ⁺ m ^a -m 2 + x m ^a X S m x m . m =0                        m =0

Пусть

∞

Fs (x) — X Smxm, m=0

тогда из предыдущего равенства имеем ma-1                /         ma-mi-1\

Fs (x) - X Smxm — xmi Fs(x) -  X Smxm + m=0             \         m=0/ ma-m2-1

F s (x) - X S m x m + x ^{m a} F s (x).

m=0/

Раскрывая скобки, получаем ma -1                           ma -mi -1

Fs(x) - X Smxm — xmi Fs(x) - xmi  X m=0

m a -m 2 - 1

+xm2 Fs (x) - xm2  X  Smxm + xmaFs (x), m=0

Fs (x) - xmi Fs (x) - xm2 Fs (x) - xmaFs (x) — ma -1              ma -mi -1              ma -m2 -1

— X Smxm - xmi  X  Smxm - xm2  X  Smxm m=0              m=0               m=0

Учитывая начальные условия (7) и рекуррентные соотношения (8) и (9), преобразуем отдельно правую часть последнего равенства:

m 3 — 1               m 3 —m i — 1               m 3 —m 2 — 1

X SmXm - xm1  X  SmXm - xm2  X  SmXm = m=0              m=0               m=0

m 2

m 1 — 1

m 2 — 1

m 3 — 1

S O + E S m X m + E S m x m + E S m x m

m = m i

m = m 2

)

-

-

m i — 1

-

x m 1

S m x ^m

+

m 3 —m i — 1

X  Smxm m=m2—mi

)

-

m 3 —m 2 — 1

x ^{m 2   X}   S m x ^m

m 2 — 1

m 3 — 1

— 1 + 0+ 52 S m x m + ^ S m X m

m 2

-

m 1 — 1

-

S _m x m + m 1

-

m = m i

m = m 2

-

m 3 —m i — 1

E C m + m i

Smx m=m2 —mi

-

m 3 -m 2

X

— 1

c _mm + m2 _ mx —

m 2 — 1

— 1 + ^X S m X ^m m = m i

m 3 — 1

+ X Smxm m=m2

-

m 2 — 1

X Sm-m1xm m=mi

-

-

m 3 — 1

X Sm-m1xm m=m2

-

m 3 — 1

X Sm-m2xm m=m2

m 2 — 1

— 1+ X m=mi

(S m

-

m 3 — 1

S m—m i ) X m + 52 (S m m = m 2

-

S m-m 1

-

S m — m 2 )X m

m 2 — 1           m 3 — 1

• — 1+ X 0 • x ^m + X 0 • x ^m — 1.

m = m i        m = m 2

Следовательно,

F s (x) (1 - x ^{m i} - x ^m 2 - x ^m 3 ) — 1,

F S (X) —

1 - x m i - x ^m 2 - x ^m 3 ,

что и требовалось доказать.

6 Частные случаи

Рассмотрим некоторые наиболее важные частные случаи.

• 6.1    Числа Трибоначчи

При m i = 1, m 2 = 2, m 3 = 3 получаем полные (m; 1, 2, 3)-покрытия (рис. 3).

m = 0 : m = 1 : m=2: m=3:

m = 4 :

•   ( S o = 1)

•—•  (Si = 1)

r

(S 2 = 2)

(S 3 = 4)

r

m = 5 :

(S 4 = 7)

r

r

rr

(S 5 = 13)

Рис. 3. Полные (m; 1, 2, 3)-покрытия

Числа S m , m ∈ N 0 в данном случае являются суммами элементов плоских сечений пирамиды Паскаля, для которых, согласно (4) и (10), один из шести вариантов расположения имеем при tgф 1 = 1, tgФ 2 = 2.

Суммы элементов этих сечений образуют последовательность чисел 1, 1, 2, 4, 7, 13, 24, 44, 81, 149, 274, 504, . . . , которая совпадает с последовательностью чисел Трибоначчи, указанной под номером A000073 в [8] и определяемой при помощи рекуррентного соотношения:

t m +3 = t m +2 + t m +i + t m , t 0 = t i = ⁰, t 2 = 1,

при этом S m — t m +2 .

Число полных покрытий в данном случае вычисляется по формуле:

[m] [m]-i Sm (1,2) = X X i=0 j=0

m — i — 2 j

i, j

и удовлетворяет, согласно (6) — (9), рекуррентному соотношению:

S m = S m - i + S m - 2 + S m - 3 , S o = S i = 1, S 2 = 2.

Производящая функция сумм элементов таких сечений, исходя из (11), имеет вид:

F S ⁽x) = 1 - Ж - Ж2 - ж3 ^. xx x

• 6.2    Числа Якобсталя

При m i = 1, m 2 = m 3 = 2 получаем полные (m; 1, 2, 2)-покрытия, при этом покрывающие отрезки, совпадающие по длине, окрашены разными цветами (рис. 4).

Числа S m , m ∈ N 0 в данном случае являются суммами элементов плоских сечений пирамиды Паскаля, для которых один из шести вариантов расположения получаем при tg ф 1 = tg Ф 2 = 1.

Суммы элементов этих сечений образуют последовательность чисел 1, 1, 3, 5, 11, 21, 43, 85, 171, 341, 683, 1365, . . . , которая совпадает с последовательностью чисел Якобсталя [6], указанной под номером A001045 в [8] и определяемой при помощи рекуррентного соотношения:

J m — Jm

1 + 2 J m- 2 , J o = 0,J i = 1,

при этом S m = J m +1 .

Число полных покрытий в данном случае вычисляются по формуле:

[m] [m]-i Sm (1,1) = X X m-i-j

i, j

i =0 j =0

и удовлетворяет, исходя из (6) — (9), рекуррентному соотношению:

S _m = S _m

1 + 2S m - 2 , S 0 = S 1 = 1.

Соответствующая производящая функция, согласно (11), имеет вид:

F S ^{( x )} = 1 - x - 2x 2 .

m = 0 : о (S o = 1)

m = 1 : о—о (S 1 = 1)

m = 2 : о—о—о о----о о----о (S 2 = 3)

m = 3 : о—о—о—о о—о----о о—о----О о----о—о о----о—о (S3 = 5)

Рис. 4. Полные (m; 1, 2, 2)-покрытия

• 6.3    Степени числа 3

При m i = m 2 = m 3 = 1 имеем полные (m; 1,1,1)-покрытия. Поскольку все покрывающие отрезки совпадают по длине, то они окрашены разными цветами (рис. 5).

Числа S _m , m ∈ N 0 в данном случае являются суммами элементов горизонтальных плоских сечений пирамиды Паскаля, для которых согласно (4) и (10), tg ф 1 = tg ф ₂ = 0.

Суммы элементов этих сечений образуют последовательность чисел 1, 3, 9, 27, 81, 243, 729, . . . , которая совпадает с последовательностью A000244 (степени числа 3) в [8].

Число полных покрытий в данном случае вычисляется по формуле:

m m-i

Sm (0, 0) = XX ’"), i=0 j=0     , и удовлетворяет, согласно (6) — (9), рекуррентному соотношению:

S m — ^{3 S} m

1 , ^S 0      ¹.

Производящая функция сумм элементов таких сечений, согласно

(11), имеет вид:

F s (x) =

1 - 3x.

m = 0 : о  (S o = 1)

m = 1 : о—о о—о  о----о

^m == 2 : О ОО О   О— —О

(S 1 = 3)

о—о----о

О----О---О О----О--О О----О----О

(S 2 = 9)

^m — 3 : О ООО О о о- -о

О--О--О---О

о—о----о—о

О---о----о---о

о- -о ...Q— о

О-.-С^— о— о   Q....Q—O- -о

О---О- -О— О О---О- -О- -О О---0— -о---о

(S 3 = 27)

Q....Q....Q— О    Q....Q....Q- -О 0----О---О---0

Рис. 5. Полные (m; 1,1,1)-покрытия

В таблице 1 приведены некоторые значения чисел m1 , m2 и m3 , последовательность Sm, m Е No чисел полных (m; mi, m2, mз)-покрытий и соответствующие этим числам углы плоских сечений пирамиды Паскаля (один из шести случаев согласно (10)), а также приведены номера этих последовательностей в [8].

Таблица 1. Полные покрытия отрезка длины m и некоторые известные комбинаторные числа

m i	m 2	m 3	S m ,m е N o	tg ф 1	tg ф 2	№ в [8]
1	2	3	1, 1, 2, 4, 7, 13, 24, 44, 81, 149, ...	1	2	A000073*
1	1	2	1, 2, 5, 12, 29, 70, 169, 408, 985, ...	0	1	A000129*
1	1	1	1, 3, 9, 27, 81, 243, 729, 2187, ...	0	0	A000244
1	2	2	1, 1, 3, 5, 11, 21, 43, 85, 171, ...	1	1	A001045*
1	3	4	1, 1, 1, 2, 4, 6, 9, 15, 25, 40, 64, ...	2	3	A006498
2	2	3	1, 0, 2, 1, 4, 4, 9, 12, 22, 33, 56, ...	0	1/2	A008346
1	1	3	1, 2, 4, 9, 20, 44, 97, 214, 472, ...	0	2	A008998
1	1	4	1, 2, 4, 8, 17, 36, 76, 160, 337, ...	0	3	A008999
2	3	4	1, 0, 1, 1, 2, 2, 4, 5, 8, 11, 17, 24, ...	1/2	1	A013979
3	3	4	1, 0, 0, 2, 1, 0, 4, 4, 1, 8, 12, 6, ...	0	1/3	A052922
1	4	4	1, 1, 1, 1, 3, 5, 7, 9, 15, 25, 39, ...	3	3	A052942
2	3	3	1, 0, 1, 2, 1, 4, 5, 6, 13, 16, 25, ...	1/2	1/2	A052947
1	2	4	1, 1, 2, 3, 6, 10, 18, 31, 55, 96, ...	1	3	A060945*
3	4	4	1, 0, 0, 1, 2, 0, 1, 4, 4, 1, 6, 12, 9, ...	1/3	1/3	A077909**
1	3	3	1, 1, 1, 3, 5, 7, 13, 23, 37, 63, ...	2	2	A077949
3	4	6	1, 0, 0, 1, 1, 0, 2, 2, 1, 3, 5, 3, 6, ...	1/3	1	A079956
1	2	5	1, 1, 2, 3, 5, 9, 15, 26, 44, 75, ...	1	4	A079971
1	4	5	1, 1, 1, 1, 2, 4, 6, 8, 11, 17, 27, ...	3	4	A079972
1	1	5	1, 2, 4, 8, 16, 33, 68, 140, 288, ...	0	4	A098588
1	2	6	1, 1, 2, 3, 5, 8, 14, 23, 39, 65, ...	1	5	A120400
1	3	6	1, 1, 1, 2, 3, 4, 7, 11, 16, 25, 39, ...	2	5	A120415
1	4	6	1, 1, 1, 1, 2, 3, 5, 7, 10, 14, 21, ...	3	5	A120446
1	5	6	1, 1, 1, 1, 1, 2, 4, 6, 8, 10, 13, 19, ...	4	5	A121832
2	3	6	1, 0, 1, 1, 1, 2, 3, 3, 6, 7, 10, 15, ...	1/2	2	A121833
1	5	5	1, 1, 1, 1, 1, 3, 5, 7, 9, 11, 17, 27, ...	4	4	A143447*
1	6	6	1, 1, 1, 1, 1, 1, 3, 5, 7, 9, 11, 13, ...	5	5	A143448*
1	7	7	1, 1, 1, 1, 1, 1, 1, 3, 5, 7, 9, 11, ...	6	6	A143449*
1	8	8	1, 1, 1, 1, 1, 1, 1, 1, 3, 5, 7, 9, 11, ...	7	7	A143450*
1	9	9	1, 1, 1, 1, 1, 1, 1, 1, 1, 3, 5, 7, 9, ...	8	8	A143451*
1	10	10	1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 3, 5, 7, ...	9	9	A143452*

Символ * рядом с номером последовательности означает, что приведенные члены последовательности совпадают с числами, указанными в [8], начиная с некоторого номера, а символ ** указывает на то, что приведенные члены последовательности являются абсолютными величинами чисел, указанных в [8].

Заключение

Полученные результаты могут играть особую роль в построении моделей машинного обучения при вычислении различных комбинаций событий; в проектировании баз данных при подсчете количества возмож- ных комбинаций данных для определения требований к их хранению; в исследовании свойств данных и прогнозировании изменений для принятия более обоснованных решений; в разработке алгоритмов машинного обучения для анализа больших объемов данных; в определении оптимальных решений для различных задач, связанных с обработкой данных, таких как управление проектами, планирование и оптимизация производственных процессов.

Рассмотренные в данной статье вопросы также имеют важное значение для развития общей теории комбинаторного анализа и решения ряда прикладных задач перечислительной комбинаторики. Дальнейшее изучение частей пирамиды Паскаля позволит расширить число соотношений между известными объектами, а также получить новые, ранее неизвестные объекты.