Моделирование потока релятивистских электронов на геостационарной орбите в магнитосфере Земли

В околоземном космическом пространстве, внутри магнитосферы Земли, в области замкнутых силовых линий магнитного поля образуется магнитная ловушка, для заряженных частиц. Эта. геомагнитная ловушка, (естественный радиационный пояс) имеет форму искаженного тороида, и содержит потоки высокоэнергичных частиц, интенсивность которых может в миллионы раз превосходить потоки частиц за. ее пределами. Принято условно считать, что естественный радиационный пояс Земли (ЕРПЗ) разделен на. два: внутренний (протонный) и внешний (электронный) [1].

Геостационарная орбита. (ГСО) космического аппарата, расположена, в плоскости географического экватора, па. расстоянии около 36 тыс. км от поверхности Земли в области внешнего ЕРПЗ. Это соответствует магнитной оболочке L « 6, 6 ( L - параметр Мак-Илвейна). В плоскости геомагнитного экватора магнитная оболочка L удалена от центра Земли на расстояние равное LRe, где R e ~ средний радиус Земли.

Потоки частиц в области ГСО подвержены как регулярным, так и не регулярным изменениям. Фактически вся динамика, частиц внешнего радиационного пояса, контролируется состоянием межпланетной среды [2]. При этом особую роль в наполнении релятивистскими электронами внешнего ЕРПЗ играют рекуррентные высокоскоростные потоки плазмы солнечного ветра. В отличие от вспышечных потоков рекуррентные потоки солнечного ветра, всегда, сопровождаются более сильными и продолжительными возрастаниями потоков релятивистских электронов во внешнем радиационном поясе.

Основной вклад в радиационные условия на. ГСО дают электроны ЕРПЗ и их тормозное излучение, потоки частиц солнечных космических лучей и потоки галактических космических лучей.

На ГСО наблюдаются периодические вариации интенсивности ионизирующих излучений, связанные с рекуррентными высокоскоростными потоками солнечного ветра, и не периодические, связанные с солнечными вспышками. При этом интенсивность релятивистских электронов на. ГСО может изменяться в течение нескольких суток более чем в десять раз и на. ГСО наблюдаются потоки электронов ЕРПЗ с энергией до 6 МэВ и протонов ЕРПЗ с энергией до 2 МэВ [3].

Существует несколько моделей для предсказания релятивистских электронов во внешнем ЕРПЗ. В работе [4] описана, модель предсказания для суточного усредненного потока, релятивистских электронов на. ГСО. Эта. модель численно решает одномерное уравнение радиальной диффузии, используя параметры солнечного ветра. В [5] использована, модель предсказания [4], чтобы развить модель прогноза, для предсказаний па. 24 часа, и 48 часов логарифма, суточного усредненного потока, релятивистских электронов на. ГСО. Эта. модель включает несколько других особенностей в дополнение к солнечному ветру. В [6] создана, модель предсказания, которая использовала, поток низкоэнергичных электронов, чтобы предсказать релятивистский поток па. ГСО. В [7] предложили осповаппую па. данных модель, чтобы получать предсказание на. одни сутки для суточного максимума, потока, электронов па. ГСО. Модель комбинирует условную вероятность с техниками нелинейного анализа, временных рядов. В [8] развили осповаппую па. физике модель среды радиационного пояса. RBE (Radiation Belt Environment), чтобы исследовать внешний ЕРПЗ и обеспечивать реальное во времени текущее предсказание популяции электронов внешнего пояса. В [9] ввели другую модель предсказания, которая предсказывает кубический корень от суточного усредненного потока, электронов с энергией >2 МэВ на. ГСО. Их метод использует два. уравнения с источниками и потерями. Модель предсказания потока. (FluxPred) [10] — это нейронная сетевая модель, использующая 17 входов, состоящих из последних 10 дней данных о потоках па. ГСО и 7 дней Кр - индекса, геомагнитной активности. Выходом нейронной сети были предсказания на. 24 часа, 48 часов и 72 часа, суточного усредненного потока, электронов с энергией >2 МэВ на. ГСО. В работе [11] рассматривается прогнозирование максимальных за. сутки значений потока, релятивистских электронов на. ГСО при помощи адаптивных методов.

В [12] представлена, улучшенная система, предсказания для релятивистских электронов на. ГСО, которая включает три реальные во времени модели предсказания. Результаты недавних измерений протонов и электронов па. ГСО и их обсуждений представлены, например, в [13, 14].

Целью данной работы является математическое моделирование потока, релятивистских электронов с энергией больше 2 МэВ па. геостационарной (геосинхронной) орбите в магнитосфере Земли. Моделирование в виде: 1) повой математической модели, описывающей дифференциальные и интегральные потоки релятивистских (>2 МэВ) электронов на. ГСО в зависимости от местного времени LT на. ГСО и Кр - индекса, геомагнитной активности, 2) аналитической формулы для оценки (при прогнозировании или предсказании) суточного максимума, потока, релятивистских ( >2 МэВ) электронов на. ГСО в зависимости от Кр - индекса, геомагнитной активности и 3) сравнения модельного потока, релятивистских (>2 МэВ) электронов с усредненными экспериментальными данными па. ГСО КА “GOES”.

1.    Математическая модель

Будем рассматривать питч-угловую диффузию в пространстве скоростей с потерями вследствие взаимодействий волна — частица, где под питч-углом а понимается угол между вектором скорости заряженной частицы и вектором напряженности магнитного поля (т.е. направлением магнитной силовой линии) в точке нахождения частицы (или ее ведущего центра). Поэтому необходим соответствующий коэффициент диффузии в пространстве скоростей, а. именно коэффициент питч-угловой диффузии. Функция потерь обусловлена, попаданием заряженных частиц в так называемый “конус потерь” в результате взаимодействий волна. - частица. Функция источника, частиц может быть связана, например, с заряженными частицами, которые движутся из хвоста, магнитосферы к Земле под влиянием магнитосферной конвекции.

Одномерное модифицированное уравнение Фоккера-Планка (или уравнение питч-угловой диффузии) для плотности фазового пространства, описывающее только “чистую” питч-угловую диффузию с потерями от взаимодействий волна-частица, может быть выражено [15, 16]

• У. = — д- ( D. sin ." - ^sin 2 ^аcos ^а A_f) - ' + _S± sin2 а • f. (1) dt sin а да da 2L dt T_wp '

Здесь, f - плотность фазового пространства, (или функция распределения): t - время; L - параметр Мак-Илвейна; а - локальный питч-угол; D.. - коэффициент питч-угловой диффузии [15, 16]; dL/dt - радиальная скорость дрейфа заряженных частиц в магнитосфере Земли [15, 16]; T_wp - время жизни вследствие взаимодействий волна - частица [15, 16]; S^ - перпендикулярный коэффициент функции источника частиц ( а = 90° ) [15, 16].

Уравнение (1) содержит некоторые математические модели “чистой” питч-угловой диффузии как частные случаи, например, [17-19].

Используя (1), как новая модель предлагается обыкновенное дифференциальное уравнение для аналитического описания перпендикулярного ( а = 90°) дифференциального потока заряженных частиц в магнитосфере Земли, которое зависит от времени и нескольких параметров:

d/ + / £ dL +    7х - 7±о \ . = о dt 2L dt 7±о (7±о + 2) Tw jX ’ где jx - перпендикулярный дпффс'репцшгльный поток заряженных частиц . = 2mEf. т - масса, заряженной частицы, E - энергия частицы), 7x0 - хорошо известный (когда j = jx sin7 а) показатель питч-углового распределения заряженных частиц (или индекс анизотропии питч-углового распределения), ио взятый для питч-угла 90° при t = 0, 7х = 7x(t) - зависимость от времени показателя питч-углового распределения заряженных частиц на. интервале времени вычисления.

При проведении численных расчетов будем полагать в уравнении (2), что dL/dt « ^dLjdtY Тогда, баупс-усредпеппая радиальная дрейфовая скорость движения заряженных частиц в магнитосфере Земли будет определена, например для дипольного магнитного поля Земли, так [20]:

( 5 ) = —П^ cosФ'                       Й'

где ф - азимутальный угол (местное время LT = 0 ч в полночь) или геомагнитная восточная долгота в плоскости магнитного экватора; П = 24 - угловая скорость вращения Земли в [1/ч]; фо = 92 кВ. а зависимость ф₂. измеренная в кВ. от геомагнитной активности, т.е. от Кр = Кр(€) - индекса, определяется по формуле [21]

0, 045

(1 - 0,16Кр + 0, 01Кр2)3 "

Тогда, уравнение (2) с учетом (3) записывается следующим образом

djx + / nф2(t)L³(t) cosф(t) +     7x(t) -7x0   \ . = 0

^dt у        ^2фо           7±о ⁽7хо^{+ 2) Т}-шр

Теперь к уравнению (5) можно добавить уравнения, описывающие траекторию движения космического аппарата. (КА), например, в гравитационном поле Земли. Но еще проще будет, если задать траекторию КА в параметрическом виде. В этом случае для ГСО (аналогично для любой круговой орбиты) получаем

L(t) = 6, 6; ф(t) = fit + р, (G)

где р = const будет определяться из сопоставления с экспериментальными данными на. ГСО. a t -это уже местное время (local time) LT вдоль ГСО.

В дальнейшем, для КА с любой круговой орбитой и с эллиптической орбитой движения такую замену в (5) можно будет делать аналогично (6).

Таким образом, в предлагаемой модели учитываются два. фундаментальных взаимодействия: электромагнитное - за. счет влияния магнитосферного электромагнитного поля па. движение заряженных частиц и гравитационное - за. счет влияния гравитационного поля Земли па. траекторию движения КА в космическом пространстве.

Для первого приближения предположим, что, например, в течение одних суток на. ГСО 7x(t) ~ 7хо ^и Кр ~ const, т.е. (4) ф₂(t) « const, тогда уравнение (5) упрощается. С учетом (6)

получается уравнение

djx /

IT +(

fiф2L3 cos(fit + р)

------2фо------ДХ =0,

которое решается аналитически

jx(t) = .хо exp

/ ^ф2^L3 - "ФФ?

[sin (fit + р) — sin

pf) •

Здесь, 33° - перпендикулярный дифференциальиый поток заряженных частиц при t = 0, т. е. когда местное время вдоль ГСО LT = 0 ч в полночь.

Дополнительно найдем перпендикулярный интегральный поток заряженных частиц. Для этого надо проинтегрировать перпендикулярный дифференциальный поток 3±(t) по энергии от какого-то значения энергии (например, E = 2 МэВ) до бесконечности (в идеале) или до очень большого значения энергии [3]. Так как левая часть и правая часть уравнения (8) не зависят от энергии, интегрирование (8) по энергии слева, и справа, дает одну и ту же константу. В итоге, получаем зависимость перпендикулярного интегрального потока заряженных частиц J (> E)^(t) от местного времени LT вдоль ГСО

J(> E)_±(t) = J(> Е)_±о exp -*2^ [sin (Qt + p) - sin pA , V  ²w                /

где J (> E )з° - перпендикулярный интегральный поток заряженных частиц в полночь на ГСО (для LT = 0 ч).

Зная из экспериментальных данных зависимости 3з° и J(> Е )з° от Кр индекса геомагнитной активности, можно будет вычислять (прогнозировать) перпендикулярный дифференциальный поток j±(t) (8) и перпендикулярный интегральный поток заряженных частиц J (> E)^(t) (9) от местного времени LT вдоль ГСО, когда Кр « const, например, в течение одних суток.

Если Kp(t) = const и (4) ф ₂ (t) = const (зависимость от t может быть сложной), получим, используя (6), следующие общие формулы для модельных (прогнозных) расчетов па. ГСО и па. любой круговой орбите КА

t cos (Qt + p)^ dt

(Ю)

(

^{3 3} № = ^{3 30 exp}J ---

И

J(> E )₃(t) = J(> E)₃₀ exp j ^— ^^(^ cos (Qt + p)^ dt.

Обычно в реальной жизни планетарный трехчасовой (в силу своего определения) Кр индекс геомагнитной активности зависит разным образом от времени. Этот индекс уже хорошо прогнозируется на. сутки, а. иногда, и на. несколько суток вперед. Поэтому чаще всего для прогноза, надо использовать формулы (10) и (11), хотя бы, вероятно, для определения тренда, основанного на. физической модели, во временном развитии потока, заряженных частиц при использовании других моделей или при сравнении с другими моделями или подходами к прогнозированию потоков, например, па. ГСО [4-12].

Для второго приближения надо использовать полное уравнение (2), по для этого еще необходимы дополнительные (теоретические и экспериментальные) исследования па. ГСО зависимости от времени показателя (индекса, анизотропии) питч-углового распределения заряженных частиц на интервале времени вычисления 73 = 73 (t) и времени жизни вследствие взаимодействий волна - частица T_wp. Поэтому в этой статье будет рассмотрено только первое упрощенное приближение для потоков заряженных частиц на. ГСО (7) - (11) с учетом (4), (6).

2.    Экспериментальные данные и расчеты

Как экспериментальные данные используются наблюдения с КА “GOES” потоков релятивистских (с энергией больше 2 МэВ) электронов, усредненные по местному часу LT вдоль ГСО с 1995 г. по 2009 г. [12]. На рис. 1 эти данные показаны кружочками и хорошо видно, что распределение усредненного интегрального потока релятивистских электронов J (> 2 МэВ)(Д от местного времени LT вдоль ГСО имеет максимум около полудня (между 1100 и 1200 LT) и наблюдается минимум потока, около полночи (между 2300 и 0000 LT). Средняя величина, этого распределения потока.

• - это суточная средняя величина, которая может быть значительно меньше, чем максимальный поток, встречаемый на. ГСО [12].

Для сравнения с результатами расчетов будем предполагать, что с хорошей точностью усредненный интегральный поток релятивистских электронов приблизительно равен перпендикулярному ( а = 90° ) усредненному интегральному потоку релятивистских электронов, т.е. на рис. 1 кружочки — это J (> 2 MdB)(t) и J (> 2 МэВ)_±Д).

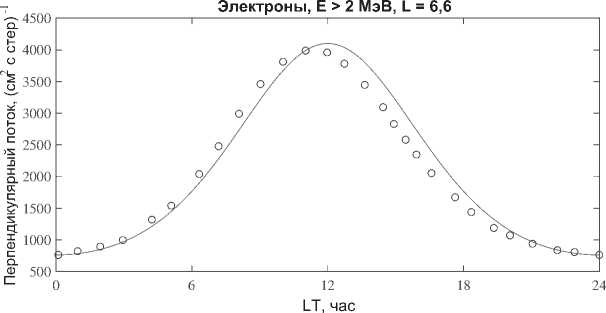
Рис. 1. Кружочками показан по данным КА “GOES” интегральный поток релятивистских электронов J (> 2 M3B)(t), усредненный по местному часу LT вдоль ГСО с 1995 г. по 2009 г.. Сплошная линия - это модельный (по формуле (12)) перпендикулярный (питч-угол а = 90° ) интегральный поток релятивистских электронов J(> 2 МsB)_±(t) в зависимости от местного времени LT вдоль ГСО.

Затем из сопоставления зависимости (9) с экспериментальными данными па ГСО (рис. 1) находим для модельного максимума потока в 1200 LT, что величина у = д/2, a J (> 2 МэВ)до и 762 электрона/(см²с стер). Отсюда получается окончательная аналитическая зависимость для усредненного перпендикулярного интегрального потока, релятивистских электронов с энергией больше 2 МэВ на ГСО, когда Кр и const, например, в течение одних суток

J(> 2 MaB)_±(t) = J(> 2 МэВ)_±о exp

Г- ^3 [cos (fit) - 1]) , ^2фо

где О 24 - угловая скорость вращения Земли в [1/ч], at- это местное время LT вдоль ГСО в часах.

Чтобы найти усредненное значение Кр индекса геомагнитной активности по экспериментальным данным (например рис. 1), надо сначала найти отношение максимального потока J (> 2 МэВ)_±(12) к минимальному потоку J (> 2 МэВ)_±(0) = J (> 2 МэВ)д₀, используя формулу (12)

J (> 2МэВ)_±(12)

J (> 2 МэВ)_±о

_    Г ^2^3 )

^exp( Ф о Л

Далее, из формулы (13) определяем ф ₂

Фо, J (> 2МэВ)_±(12) —77 Ш  7----------7 L³     J (> 2 МэВ)_±о

а потом, используя (4), Кр индекс геомагнитной активности.

По экспериментальным данным на рис. 1 максимальный поток J (> 2 МэВ)_±(12) и 4100 электронов (см²с стер), поэтому формула. (14) даст ф ₂ и 0.5385 кВ или усредненное за. сутки Кр и 5,2215 (по Международной классификации примерно Кр = 5+). Именно усредненное значение Кр, так как учитывались потоки релятивистских электронов с энергией больше 2 МэВ, усредненные по местному часу LT па. ГСО примерно за. 15 лет с 1995 г. по 2009 г. [12].

Теперь известно все необходимое для того, чтобы по формуле (12) построить сплошную кривую для сопоставления с экспериментальными данными на. рис. 1.

Ясно видно, что даже для первого приближения (12) наблюдается хорошее согласие, особенно с 0000 LT до 1100 LT и с 1800 LT до 2400 LT.

Используя аналитическую зависимость (12), найдем среднюю величину перпендикулярного интегрального потока релятивистских электронов с энергией больше 2 МэВ на ГСО, когда Кр « 5,2215 в течение одних суток, по формуле

У (> 2 МЗВЫ = ^J( >²¹ U .—- _МШ) - 1]) d,         (15)

24 У \ 20о             у где t - местное время LT вдоль ГСО в часах.

Подставляя в (15) соответствующие дополнительные данные, получаем, что (J(> 2 МэВ)^) « 2095 электронов/(см2с стер). Тогда как средняя величина группы данных КА “GOES” для потоков релятивистских (с энергией больше 2 МэВ) электронов, усредненных по местному часу LT па. ГСО с 1995 г. по 2009 г. [12] (рис. 1), (J(> 2 МэВ)) « 2050 электронов/(см2с стер).

Поэтому относительная погрешность для этих величии получается такая е = 2095—0050 1 00% ~ 2, 2%, что говорит в космической физике в целом об очень хорошем соответствии между моделью и экспериментальными данными.

Иногда, еще вычисляют суточные флюенсы релятивистских электронов внешнего радиационного пояса. Земли, в том числе и па. ГСО. При этом под флюенсом (fluence), в общем, понимается интеграл по времени от плотности потока, частиц или энергии. Здесь рассмотрим суточный флюенс от модельного распределения (12) перпендикулярного интегрального потока, релятивистских электронов с энергией больше 2 МэВ на ГСО, имеющего размерность [электроны/(см²с стер)]. Поэтому берем телесный угол 4т стер, временной интервал t = 24 ч LT и используем следующую формулу для расчета, модельного (прогнозируемого) суточного флюенса.

F (> 2 МэВ)_± = 4 tJ (> 2 МэВ)_±о3600

И. '£

[cos(fit) — 1]^ dt,

где t - местное время LT вдоль ГСО в часах, но после интегрирования в (16) размерность времени [ч] переводится в [с]. Тогда итоговая размерность для флюенса [электроны/(см2)], как это и должно быть. Подставляя в (16) соответствующие дополнительные данные, в том числе Кр « 5,2215 в течение одних суток, получаем, что F (> 2 МэВ)^ « 2,27 10⁹электронов/(см²).

Формула. (16) справедлива, тогда, когда, в течение одних суток индекс геомагнитной активности Кр = const или Кр « const. Если Kр(t) = const и (4) 02 (t) = const, надо сначала воспользоваться формулой (11), чтобы найти J (> Е )±(t), а затем по найденному распределению от времени найти модельный (прогнозируемый) суточный флюенс аналогично (16). Но, вероятно, более адекватно, так как используется перпендикулярный (питч-угол а = 90° ) интегральный поток релятивистских электронов, не умножать на 4т стер и тогда получаем следующий вариант определения модельного суточного флюенса (16) в других единицах измерения F (> 2 МэВ)^ « 1,81 10⁸ электронов/(см²стер), используя усредненные с 1995 г. по 2009 г. экспериментальные данные КА “GOES” [12] па. рис. 1.

На рис. 2 па. ГСО представим модельное (прогнозируемое) отношение максимального интегрального потока J (> 2 М эВ)±(12) (в полдень) к минимально му интегральному потоку J (> 2 МэВ)±(0) = J(> 2 МэВ)хо (в полночь) в зависимости от Кр индекса геомагнитной активности, используя для этого (13) и (4). При этом надо заметить, учитывая (8), что формула. (13) справедлива. и для отношения аналогичных дифференциальных потоков. Таким образом, получается очень интересная нелинейная зависимость, когда примерно в течение одних суток Кр = const или Кр « const. Так как правая часть (13) не зависит от энергии заряженных частиц, эту теоретическую зависимость от Кр индекса можно назвать “идеальной” или “универсальной” для прогнозирования. Возможно, она. будет предельной для оценки отношения потоков.

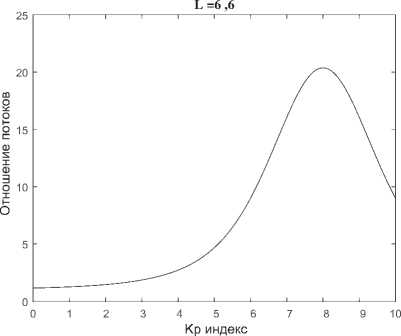
Рис. 2. Сплошная линия - это модельное (прогнозируемое) отношение максимального интегрального потока J (> 2 МэВ)_±(12) (в полдень) к минимальному интегральному потоку J (> 2 МэВ)_±(0) = J (> 2 МэВ)то (в полночь) в зависимости от Кр индекса геомагнитной активности. Эту теоретическую зависимость от Кр индекса можно назвать “идеальной” или “универсальной” для прогнозирования.

Далее будет приведена, примерная классификация состояния магнитосферы Земли [3] по величине трехчасовых значений планетарного Кр индекса геомагнитной активности.

Если магнитосфера Земли спокойная (0 <  Кр <  4) отношение потоков меняется мало (от 1,15 до 2,72) (рис. 2). Если магнитосфера возбужденная (4 <  Кр <  5), то отношение потоков меняется от 2,72 до 4,68. Если слабая магнитная буря (5 <  Кр <  6) отношение потоков меняется от 4,68 до 9,0. Если средняя магнитная буря (6 <  Кр <  7) отношение потоков меняется от 9,0 до 16,06. Если сильная магнитная буря (7 <  Кр <  8) отношение потоков меняется от 16,06 до 20,37, т.е. до максимального значения отношения потоков на рис. 2. Если очень сильная магнитная буря (8 <  Кр <  9), что бывает редко, отношение потоков меняется уже в сторону уменьшения от 20,37 до 16,06, т.е. прогнозируется симметричный спад относительно Кр = 8. И если экстремально сильная магнитная буря (9 <  Кр <  10), что бывает очень редко, отношение потоков продолжает уменьшаться от 16,06 до 9,0, т.е. прогнозируется дальнейший симметричный спад относительно Кр = 8. Таким образом, теоретическая (модельная) зависимость на рис. 2 прогнозирует для Кр >  8 спад отношения потоков, несмотря на увеличение Кр индекса геомагнитной активности. Это кажется особенно интересным и неожиданным не только с теоретической точки зрения и прогнозирования. Поэтому необходимо обратить внимание на. соответствующие экспериментальные данные для сравнения теории с экспериментом. В целом, строгая симметрия в теории наблюдается от Кр = 6 до Кр = 10 с максимумом отношения потоков по предложенной модели (13), (4) только в 20,37 раза (это теоретический предел) при Кр = 8 (рис. 2). Но самое главное, формула (13) вместе с (4) позволяет па. сутки вперед практически “мгновенно” прогнозировать в будущий полдень максимальный (интегральный или дифференциальный) поток релятивистских электронов на. ГСО, если известен поток в полночь и примерно в течение одних суток Кр = const или Кр « const. Такое прогнозирование очень важно, например, при использовании электронной аппаратуры па. КА, находящемся па. ГСО.

Заключение

Предложена новая математическая модель, описывающая аналитически (когда Кр = const или Кр « const) и численно (если Кр(£) = const) перпендикулярные дифференциальные и интегральные потоки релятивистских электронов с энергией больше 2 МэВ на. геостационарной (геосинхронной) орбите в магнитосфере Земли, а. также на. любой круговой орбите в зависимости от местного времени LT на орбите и Кр - индекса геомагнитной активности.

Как экспериментальные данные использованы наблюдения с КА “GOES” потоков релятивистских (с энергией больше 2 МэВ) электронов, усредненные по местному часу LT вдоль ГСО с 1995 г. по 2009 г.. При сопоставлении с усредненными экспериментальными данными модельного перпендикулярного интегрального потока, релятивистских электронов с энергией больше 2 МэВ на. ГСО, когда Кр « const, например, в течение одних суток, наблюдается хорошее согласие, особенно с 0000 LT до 1100 LT и с 1800 LT до 2400 LT.

Средняя величина, модельного перпендикулярного интегрального потока, релятивистских электронов с энергией больше 2 МэВ на. ГСО определена, с относительной погрешностью приблизительно 2,2 % по отношению к аналогичной средней величине по экспериментальным данным.

Предложена, формула, для расчета, модельного (прогнозируемого) суточного флюенса, от перпендикулярного интегрального потока, релятивистских электронов с энергией больше 2 МэВ на. ГСО.

Получена, аналитическая формула, для определения модельного (прогнозируемого) отношения максимального интегрального потока, (в полдень) к минимальному интегральному потоку (в полночь) в зависимости от Кр индекса геомагнитной активности. Формула представлена графически в виде нелинейной зависимости, когда Кр изменяется от 0 до 10. При этом наблюдается строгая симметрия от Кр = 6 до Кр = 10 с максимумом отношения потоков по предложенной модели только в 20,37 раза (это теоретический предел) при Кр = 8.

Эта. же формула, позволяет па. сутки вперед практически “мгновенно” прогнозировать в будущий полдень максимальный (интегральный или дифференциальный) поток релятивистских электронов на ГСО, если известен поток в полночь и примерно в течение одних суток Кр = const или Кр « const, что очень важно, например, при использовании электронной аппаратуры на КА, находящемся па. ГСО.