Моделирование поверхности головки височно-нижнечелюстного сустава человека в связи с частичной кондилэктомией

Нижняя челюсть человека соединяется с черепом посредством двух височнонижнечелюстных суставов. Между двумя соответствующими поверхностями костей расположен суставной диск, который, как считается, уменьшает контактное давление путем увеличения области контакта между неконгруэнтными суставными поверхностями. Клинические исследования показали, что височно-нижнечелюстной сустав человека часто нагружен при работе. Вырождение суставных тканей и перегрузка приводят к некоторым нарушениям функционирования височнонижнечелюстного сустава. Аналитические и численные модели жевательной системы человека, включающей височно-нижнечелюстной сустав, могут служить мощными инструментами анализа действующих на сустав нагрузок, влияния давления и распределения напряжений.

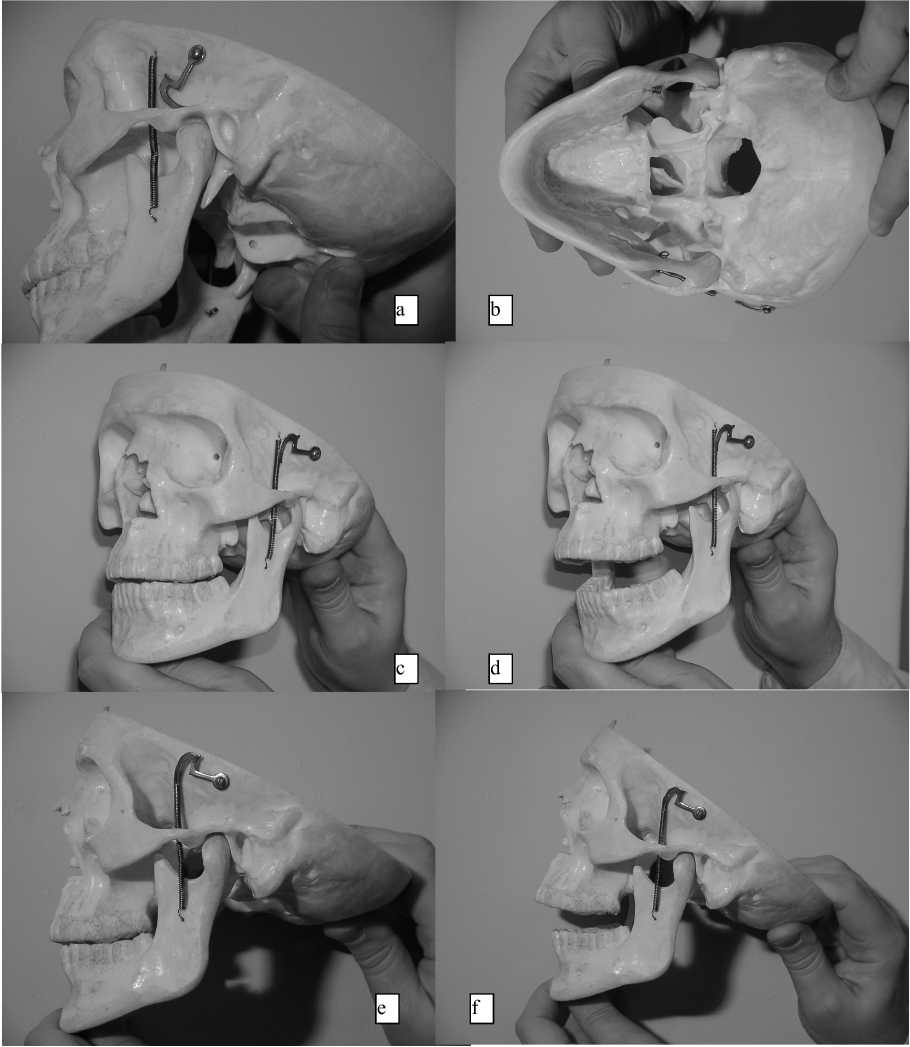
Рис. 1. Модель височно-нижнечелюстного сустава: a – вид сбоку при окклюзии; b – вид c основания черепа при окклюзии; c – вид спереди; начало фазы открывания; головка нижней челюсти в центральном положении; d – вид спереди; фаза полного открытия; головка нижней челюсти в передней части сустава; e – вид сбоку; начало фазы открывания; головка нижней челюсти в центральном положении; f – вид сбоку; фаза полного открытия; головка нижней челюсти в передней части сустава

В литературе упоминаются некоторые аналитические модели, которые описывают механику височно-нижнечелюстного сустава [3, 9, 16, 19, 20]. С другой стороны, некоторые авторы проводят численное описание височно-нижнечелюстного сустава, используя метод конечных элементов [1, 2, 17]. Есть также исследования по геометрии головки нижней челюсти и височно-нижнечелюстного сустава [7, 8]. В некоторых работах рассматриваются проблемы механики суставов [11, 12, 15, 18]. В ряде статей изложены анатомические и клинические проблемы суставов человека, включая суставы нижней челюсти [5, 6, 13, 14]. Анатомия височно-нижнечелюстного сустава представлена в известных монографиях [4, 10].

Новизна настоящей работы по сравнению с упомянутыми состоит: 1) в получении аналитических выражений для коэффициентов Ламе, которые могут быть использованы при постановке и решении задачи о гидродинамической смазке в височно-нижнечелюстном суставе; 2) в анализе частичной кондилэктомии головки нижней челюсти. Использование аналитических и численных моделей височнонижнечелюстного сустава может быть полезно при разработке протезов и в клинической практике.

Некоторые примеры движений височно-нижнечелюстного сустава при дыхании, глотании слюны и кусочков пищи и при разговоре показаны на рис. 1a–f.

Аналитическое нахождение коэффициентов Ламе в эллипсоидальной системе координат

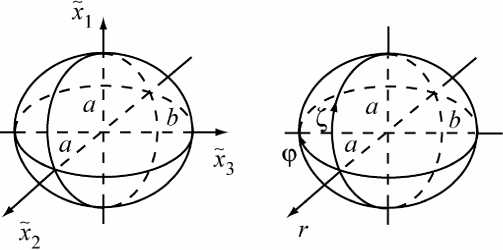
Известно, что головка и впадина височно-нижнечелюстного сустава человека имеют характерную геометрию (рис. 2a–b). В данной работе учитывается эллипсоидальная форма головки нижней челюсти. Необходимо определить коэффициенты Ламе для поверхности эллипсоида. Уравнение поверхности эллипсоида вращения имеет в декартовой системе координат ( x 1 ,x ₂, x₃) следующий вид (рис. 3a), [3]:

xxx

2 + 2 + Z,2

aab где a < b . Длины осей эллипсоида равны 2а и 2b в метрах. Параметрические уравнения поверхности этого эллипсоида имеют вид

Г Z )                             fZГZ )

х1 = а • sin I — I cos(ф), x2 = а • sin I    I sin(ф), x3 = b • cos  II

I a )                         I a )                           I п п Z где — < ф < —, 0 < — < 2п и a < b . Переменная ф отвечает окружному направлению, Z 22a

– меридиональному направлению и r – радиальному направлению в [м] (рис. 3b).

Радиус-вектор r 0 точки поверхности может быть записан следующим образом (рис. 4a):

где

^r 0 =

Г о = Х 1 1 + x 2 j + x 3 k

fZ)

a sin — cos ф 1 + a sin I a J

Z

Z ) •       • A f Z

- I sin ф j ⁺ b cosI -

k.

a

a

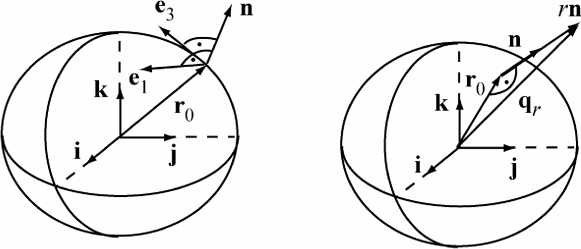
Единичные векторы e ₁ , e ₃ имеют вид [3, 19, 20]:

5 r o

5 r₀ e i = ЧТ0 • „ 5ф 5ф

5 r₀ и e₃ = —⁰ •

³ 5Z 5Z

5 r o

- 1

.

a

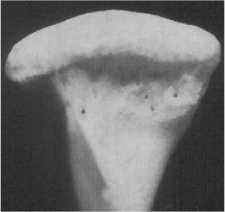
Рис. 2. Вид спереди головки нижней

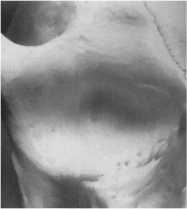
b

челюсти (a) и впадина височно-нижнечелюстного

сустава (b)

a                               b

Рис. 3. Декартова x 1 , x₂,х₃ (а) и эллипсоидальная ортогональная ф , r , Z (b) системы координат

a                                   b

Рис. 4. Геометрическая интерпретация векторов e ₁, e ₁, n (a) и r ₀, q _r (b)

Подставляя (4) в (5), получим для e ₁ , e ₃ :

e 1 = ( - sin ф ) i + (cos ф ) j + 0 • k ,

^e 3 =

cos

S 1

/

Z

\

cos ф I + —cos - sin ф J + _    L S i

V a J

b 1

---sin a S1

k,

(Z

S 1 = cos² I —

a

+ bZ sin 2 ^(Z a ²

.

a J

Вектор нормали n определяется формулой [3, 19]:

n = e 1 x e ₃ =

- sin ф

¹     (Z)

— cos I — I cos ф S 1     V a J

j cos ф

1     (Z) •

— cos I — I sin ф

S 1     V a J

k

b 1

---sin a S1

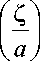
Окончательный вид вектора n следующий:

n =

b 1 • (Z) ---sin I — I cos ф aS1   V a J

i +

b 1 - (Z) ----sin I — I sin ф a S1    V a J

j +

--cos

S 1

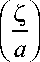
k ,

где S 1 выражается формулой (8). Радиус-вектор q _r слоя имеет вид (рис. 4b):

q r = r + r , n ^ X 1 i + x 2 j + Х з к ,                           (11)

где радиус-вектор r ₀ точки поверхности определяется соотношением (4) и вектор нормали n – формулой (10).

Подставляя (4) и (10) в (11), получим:

x 1 i + x 2 j + x ₃ k ^

- (Z) r ( b ) . (Z)

i +

a sin I — I cos ф+--I — I sin I — I cos ф

V a J        S 1 V a J   V a J

+

■ fZY , r ( a sin I — I sin ф+--I

V a J        S 1 V

b (Z)

— I sin I — I sin ф a J   V a J

j +

( Z b cos I —

V a

r (Z

--cos I —

S 1     V a

k = q r .

Сравнив коэффициенты в левой и правой частях (12), получим систему параметрических уравнений для слоя в виде:

. (z) r ( b ) . (Z)

x 1 = a sin I — I cos ф+--I — I sin I — I cos ф ,

V a J        S 1 V   a J   V a J

( Z )       r ( b )   ( Z )

x 2 = a sin I — I sin ф+--1 — I sin I — I sin ф ,

V a J        S 1 V   a J   V a J

= b cos

r (Z

--cos —

S 1    V a

x ₃

где S 1 выражается формулой (8).

Коэффициенты Ламе имеют, как известно, следующий вид [3, 19, 20]:

hm = i	( 5 x 1 )	2	+	(5 x 2 )	2	+	(5 x 3 )	2	(16)
ф   Д	V д ФJ			V5ф;			V5ф;
hr =ii	I	2	+	(3 x 2	2	+	(5 x 3	2	(17)
r	V 5 r J			<5 r J			v 5 r J
h Z = ^	( d x 1	2	+	(5 x 2 )	2	+	(5 x 3 )	2 .	(18)
	VdZ J			d-			VdZ J

Подставляя (13)–(15) в (16)–(17), найдем коэффициенты Ламе для произвольного эллипcоидального слоя в виде:

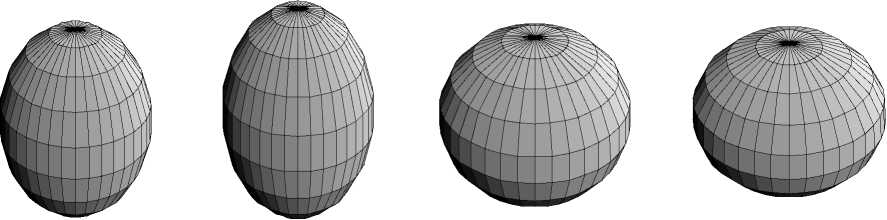
a                       b                         c                           d

Рис. 5. Компьютерное моделирование эллипсоидальной поверхности головки нижней челюсти. Параметры: a – 2a=20 мм, 2b=28 мм; b – 2a=20 мм, 2b=32 мм; c – 2a=26 мм, 2b=24 мм; d – 2a=30 мм, 2b=24 мм hz (r, Z) - , cos

[z

hф(r,z) - asin

V a

2 [Z

1 —

a

V

T

— b ¹ sin

S 1

h_r - 1,

T 1 b

z

a

,

S 3 a J

+

—

b . [z - sin I

V a

a

. ^i b 2 ■

+ r^-sin

S ₁ ³ a ²

z

a

J

,

r ^ 1 - -,

a

Таблица 1

Значения длин осей 2 a и 2 b для эллипсоидальной головки нижней челюсти, мм

Эллипсоидальная головка нижней челюсти	Источник			Численный расчет [Авторы]
	Синельников [4]	Łasiński [10]	[Авторы]
Длина 2 a	18,75–20	18–20	18–22	20, 24, 28, 32
Ширина 2 b	6,25–7,5	5–15	8–9	18, 22, 26, 28

„ z „ где 0 < r <8 , 0 < — < 2n, a < b и через 8 обозначена толщина слоя в метрах. a

Коэффициенты Ламе для тонкого эллипсоидального слоя получаются при

^ 1 ^ 0. Окончательно коэффициенты Ламе в эллипсоидальных координатах равны:

rzi hф(z) - a sin I    I,

V a J hr -1,

h z ( z )-. cos^{2 [z} V V a

b ² - ₂[z + -ysin²

a ²      V a

,

ζζ где 0 ≤ ≤ 2π , a < b . Величины ϕ ,   , hr , hζ безразмерны; размерности других aa величин: [r]=[м], [ζ]=[м], [a]=[м], [b]=[м], [hϕ]=[м] и [ε]=[м]. Принятые в численных расчетах длины осей для головки нижней челюсти показаны в табл. 1.

Компьютерное моделирование эллипсоидальной головки нижней челюсти

Результаты компьютерного моделирования с использованием лицензионного пакета “Mathematica 4.1” приведены на рис. 5a–d. На рис. 5a, b показано изменение большей оси эллипсоида 2 b , а на рис. 6c, d показано изменение меньшей оси 2 a . Программы, написанные в пакете “Mathematica 4.1” , приведены в табл. 2. Перед использованием программ следует ввести строку <

Таблица 2

Примеры программ в пакете “Mathematica 4.1”

Рис	Программа компьютерного моделирования:	Полуоси		Углы
		a	b	u ≡ζ	v ≡ϕ
5a	ParametricPlot3D[({10 ∗ Sin[u/10]) ∗ Cos[v], (10 ∗ Sin[u/10] ∗ Sin[v], (14 ∗ Cos[u/10])}, {u, 0, 10 ∗ 2Pi}, {v, -Pi/2, Pi/2}, Axes->False, Boxed->False, ColorOutput->GreyLevel]	10	14	<0,20 π >	ππ - 2 , 2
5b	ParametricPlot3D[({10 ∗ Sin[u/10]) ∗ Cos[v], (10 ∗ Sin[u/10] ∗ Sin[v], (16 ∗ Cos[u/10])}, {u, 0, 10 ∗ 2Pi}, {v, -Pi/2, Pi/2}, Axes->False, Boxed->False, ColorOutput->GreyLevel]	10	16	<0,20 π >	ππ - 2,2
5c	ParametricPlot3D[({13 ∗ Sin[u/13]) ∗ Cos[v], (13 ∗ Sin[u/13] ∗ Sin[v], (12 ∗ Cos[u/13])}, {u, 0, 13 ∗ 2Pi}, {v, -Pi/2, Pi/2}, Axes->False, Boxed->False, ColorOutput->GreyLevel]	13	12	<0,26 π >	ππ - 2 , 2
5d	ParametricPlot3D[({15 ∗ Sin[u/15]) ∗ Cos[v], (15 ∗ Sin[u/15] ∗ Sin[v], (12 ∗ Cos[u/15])}, {u, 0, 15 ∗ 2Pi}, {v, -Pi/2, Pi/2}, Axes->False, Boxed->False, ColorOutput->GreyLevel]	15	12	<0,30 π >	ππ - 2 , 2

Случай пациента с частичной кондилэктомией головки нижней челюсти

Пациент P.S., возраст 62 года, госпитализирован в отделение челюстно-лицевой и зубной хирургии, с жалобами на боль в области височно-нижнечелюстного сустава (рис. 6). Пациент имел частичную кондилэктомию левой головки нижней челюсти (рис. 6). Во время операции хирурги удалили часть поверхности головки нижней челюсти с покрывающим хрящом. После операции болевые ощущения в области височно-нижнечелюстного сустава оставались. Пациент был направлен в отделение зубного протезирования с диагнозом “дисфункция височно-нижнечелюстного сустава” для дальнейшего консервативного лечения.

При исследовании и на пантомографической рентгенограмме, датированной 21 сентября 2002 г. (рис. 6), наблюдалась потеря боковых зубов, соответствующая классификации Eichner B4. По словам пациента, он использовал только регулируемый съемный верхний протез.

Пациенту было назначено протезирование. Дополнительно была изготовлена межзубная шина для стабилизации окклюзии. Была рекомендована общая терапия с применением болеутоляющих и противовоспалительных средств. Пациент прошел курс лечения салициловыми и лигнокаиновыми препаратами, а также электротерапию.

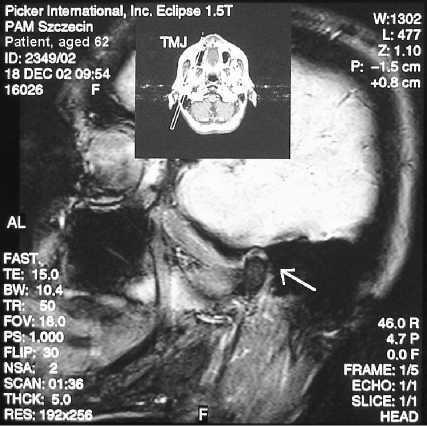
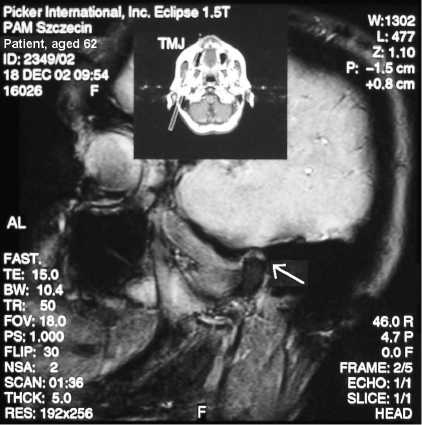
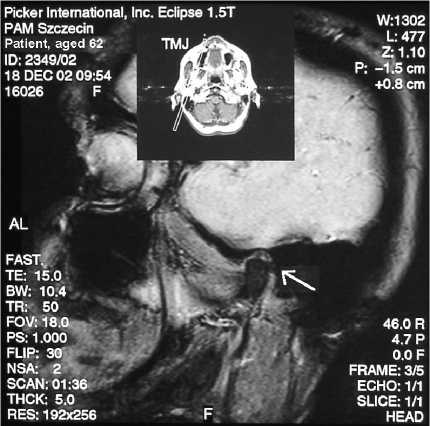
Для данного пациента был получен ряд компьютерно-томографических снимков левого и правого височно-нижнечелюстных суставов. Движения правого сустава показаны на рис. 7a–d. На первом и втором кадрах показаны два этапа фазы окклюзии (рис. 7a, b); на третьем и четвертом – два этапа фазы открывания (рис. 7c, d).

Можно видеть не только движение головки нижней челюсти (см. стрелки), но также элементы височно-нижнечелюстного сустава. Представляет интерес анализ поверхности головки нижней челюсти.

Движения левого височно-нижнечелюстного сустава показаны на рис. 8a–d. На первом и втором кадрах показаны два этапа фазы окклюзии (рис. 8a, b); на третьем и четвертом – два этапа фазы открывания (рис. 8c, d).

Можно видеть не только движение головки нижней челюсти (см. стрелки), но также элементы височно-нижнечелюстного сустава. Представляет интерес наблюдение поверхности поврежденной левой головки нижней челюсти.

В результате проведенного лечения было достигнуто некоторое снижение болевых ощущений (рис. 9).

Обсуждение

Болевые ощущения являются основными и трудноустранимыми симптомами заболеваний височно-нижнечелюстного сустава. Для устранения болей применяется операция частичной кондилэктомии. При этой операции удаляется часть поверхности мыщелкового отростка нижней челюсти.

Предварительный план операции основывается на визуальной диагностике. Имеются, например, рентгеновские технологии ( RTG -снимки, пантомографические рентгенограммы нижней челюсти) и магниторезонансные технологии. Операция в области височно-нижнечелюстного сустава часто изменяет механику его функционирования.

Анализ геометрии соприкасающихся поверхностей головки нижней челюсти и суставной впадины может быть полезным при планировании операций в области височно-нижнечелюстного сустава.

Информация о параметрах функционирования височно-нижнечелюстного сустава, особенно о давлении, напряжениях и нагрузках, поможет при диагностировании и лечении заболеваний.

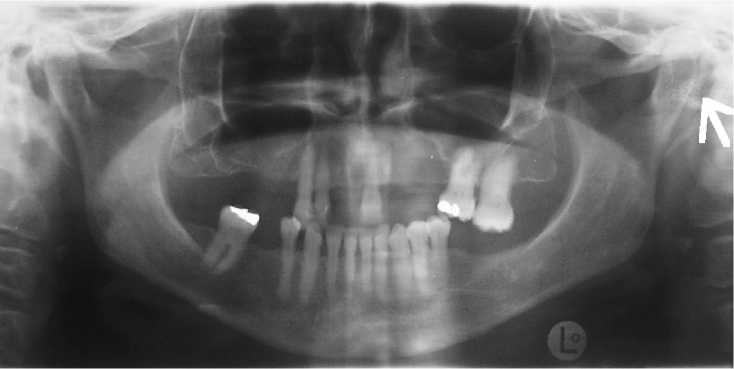
Рис. 6. Пантомографическая рентгенограмма перед операцией, 21 ноября 2002

a

b

c

Рис. 7. Компьютерно-томографические снимки правого височно-нижнечелюстного сустава (a, b – окклюзия, c, d – открывание). До операции, 18.12.2002

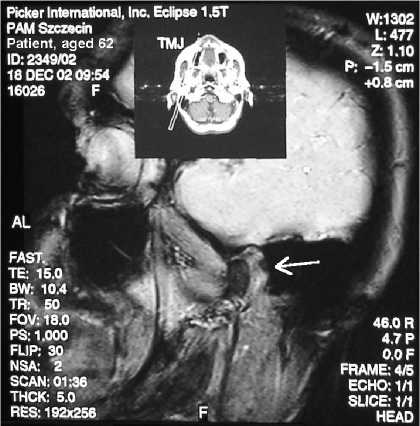
d

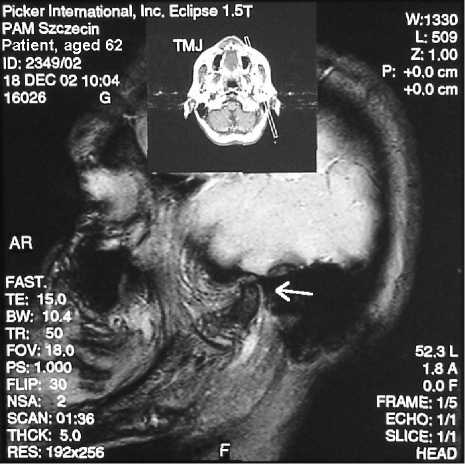
a

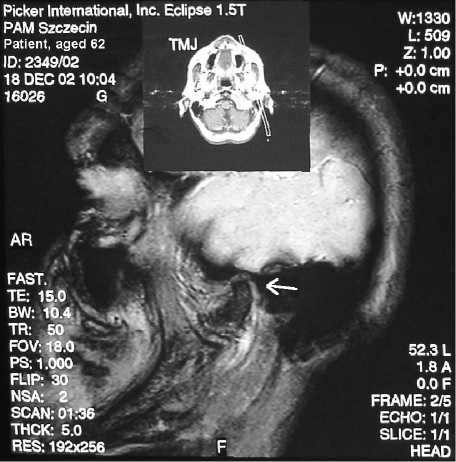
b

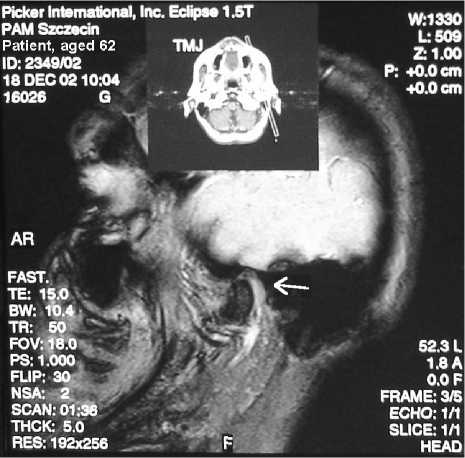
c

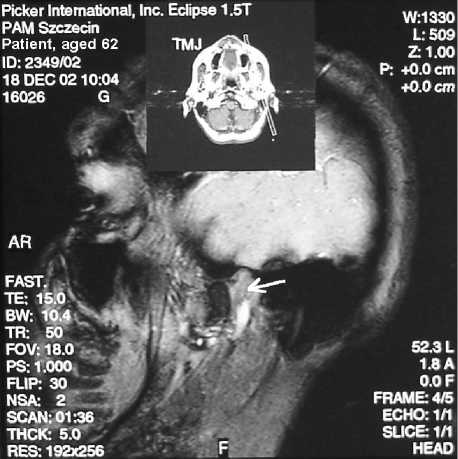
d

Рис. 8. Первый компьютерно-томографический снимок левого височно-нижнечелюстного

сустава (a, b – окклюзия, c, d – открывание). До операции, 18.12.2002

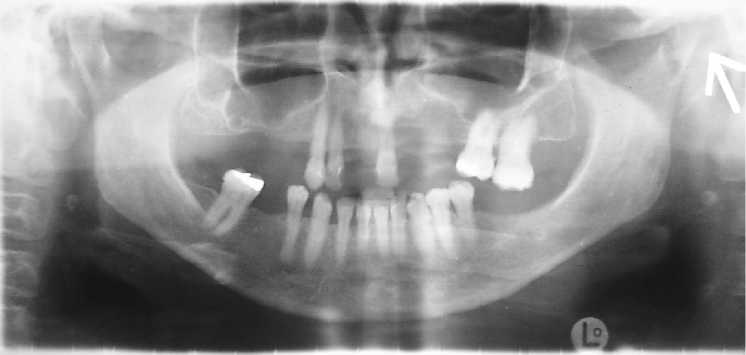
Рис. 9. Пантомографическая рентгенограмма после операции, 14 января 2003 г. Можно видеть хирургическое вмешательство на левой головке нижней челюсти

Выводы

На основе клинической практики, аналитических и численных расчетов можно сделать следующие выводы.

• •    Клинические наблюдения показывают, что головки нижней челюсти человека могут иметь разнообразные геометрические формы. Предположение об эллипсоидальности формы позволяет построить приемлемую аналитическую модель. Можно записать в явном виде уравнение поверхности эллипсоида вращения. Можно также использовать параметрические формулы для перехода от декартовой к эллипсоидальной системе координат.

• •    Используя модель эллипсоидальной поверхности височно-нижнечелюстного сустава, можно найти коэффициенты Ламе как для произвольного, так и для тонкого эллипсоидального слоя в эллипсоидальных координатах.

• •    Вычисленные коэффициенты Ламе могут быть использованы в основных уравнениях задачи гидродинамической смазки в височно-нижнечелюстном суставе. В этом случае необходимо составить систему уравнений, описывающих несимметричное и нестационарное течение синовиальной жидкости между двумя суставными поверхностями

• •    Знание геометрии головки нижней челюсти может быть очень полезно при выборе и уточнении плана операции в области височно-нижнечелюстного сустава.