Моделирование процесса абразивной обработки внутренних теплозащитных покрытий с учетом взаимодействия упругой и тепловой систем

приповерхностных слоях материала вызывают значительные механические и тепловые нагрузки, приводящие иногда к трещинам и прижогам на обработанных поверхностях, что ухудшает качество обработки. С другой стороны, высокие температуры при шлифовании воздействуют на шлифовальный круг, приводят к выгоранию связки, затуплению зерен, повышенному износу, что снижает производительность и ухудшает условия обработки [4]. Обработка теплозащитного покрытия производилась на токарновинторезном станке модели 166 при помощи шлифовальной головки (рис. 1).

Шлифовальная головка крепится на трубе-качалке, которая является несущей конструкцией установки и монтируется на продольном суппорте токарного станка. Внутри трубы-качалки расположены электропроводка, воздушные шланги, необходимые для обдува зоны обработки и охлаждения двигателя, гаситель колебаний и система рычагов для обеспечения необходимой силы прижатия абразивного круга к обрабатываемой поверхности. Шлифовальная головка состоит из асинхронного электродвигателя переменного тока типа АИР 80 В4, редуктора и шпинделя со шлифовальным кругом. Для обработки теплозащитного покрытия использован шлифовальный круг 1-180x20x32 25AF36OBF 30 м/с, который имеет на периферии проточки с шагом 12 градусов для обеспечения прерывистого шлифования.

Качество поверхности при абразивной обработки теплозащитных покрытий оценивается не только по точности выполненных размеров, но и по ряду специфических признаков: наличию вырывов, отслоений, разнотонности обработанного покрытия, появление которых зачастую является следствием потери режущей способности абразивного круга. Потеря режущих свойств в большинстве случаев связана с «засаливанием» рабочей поверхности круга. Причиной «засаливания» является то, что в процессе обработки изношенные зерна и частицы обрабатываемого материала, окружающие зерно, не успевают удаляться из зоны обработки. Засаливание приводит к повышению температуры в зоне обработки, в результате возможно превышение теплоемкости связки абразивного инструмента и преждевременное выкрашивание зерна абразива. В силу низкой теплопроводности теплозащитного покрытия тепло локализуется в зоне резания, что приводит к нагреву поверхностного слоя обрабатываемого материала и периферийных зерен абразивного круга, вызывающему преждевременное выкрашивание абразивных зерен, т.к. силы сцепления зерен со связкой в этом случае существенно понижаются.

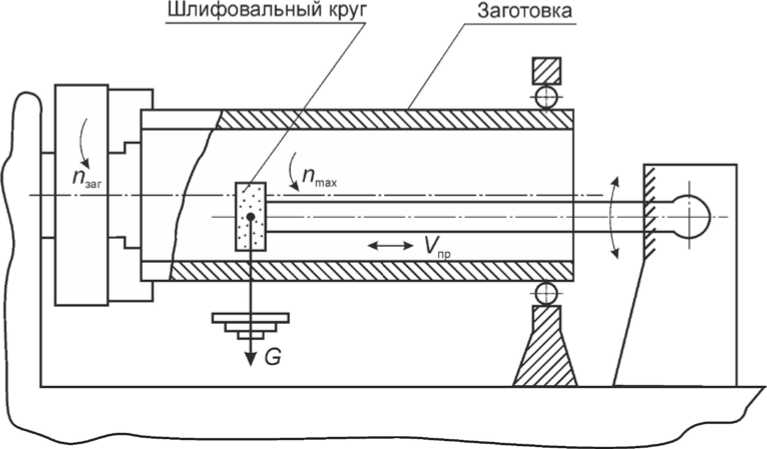
Рис. 1. Схема обработки теплозащитного покрытия

Цель работы : определение температурносиловых параметров при абразивной обработке поверхностей теплозащитных покрытий на основе моделирования технологической системы, включающей упругую систему, процесс резания и тепловые процессы.

Задачей математического моделирования процесса абразивной обработки теплозащитного покрытия является установление взаимосвязи между параметрами обработки (подача, глубина и скорость резания, ширина круга, зернистость и т.д.) и силами резания при температурах, допускаемых условиями работы абразивного инструмента [5]. Схема контактного взаимодействия абразивного инструмента и обрабатываемого материала представлена на рис. 2, где C Y , C Z - жесткость опор шлифовального круга по осям Y и Z ; V К и V И - окружная скорость круга и обрабатываемой детали (изделия); R Y и R Z - элементы сопротивлениямеханической системы перемещениям в направлениях Y и Z ; t- глубина резания, / _д - длина линии контакта.

Характер взаимодействия инструмента и обрабатываемой поверхности определяются, прежде всего, работой абразивных зерен как основных режущих элементов. Изучение работы единичного зерна позволяет получить расширенные представления о силах резания, процессе износа и температуре зоны контакта зерна с обрабатываемой поверхностью.

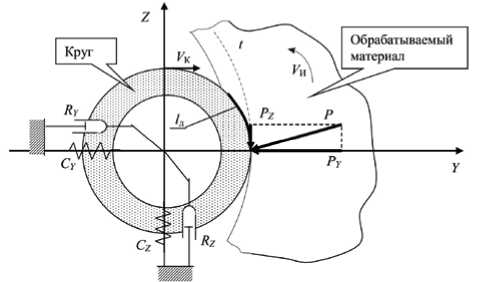
Рис. 2. Схема контакта шлифовального круга с обрабатываемым материалом

Силы резания, представленные на рис. 2, могут быть вычислены в соответствии со следующими выражениями:

P , = 2 Р з Y,

+ p + p

⁺ Св Y ⁺ Ст Y ,

P_Z = У PZi

Z          З Zi

^{+ Р} Св Z

+ p

⁺ Ст Z ,

где P _{З Yi} , P _{З Zi} , P _{Св Y} , P _{Св Z} , P _{Ст Y} , P _{Ст Z} – радиальная и тангенциальная составляющие силы резания соответственно при микрорезании единичным зерном; от контакта материала со связкой круга; от контакта материала со стружкой, заполняющей поры круга.

Кинематика процесса абразивной обработки определяется главным образом величиной P З. Составляющие P Св и P Ст мало зависят от относительного смещения круга и заготовки, и их

можно принять постоянными величинами и учесть в модели постоянными внешними усилиями. Схема процесса абразивной обработки для определения составляющих силы резания представлена на рис. 2, где F ТР – сила трения, F УП – сила сопротивления прижиму круга.

При прохождении абразивным зерном зоны контакта детали с кругом силы резания изменяются синхронно с изменением глубины микрорезания a . Ширина площадки на вершине абразивного зерна связана с глубиной микрорезания зерна и с учетом формы зерна можно принять b =2 a .

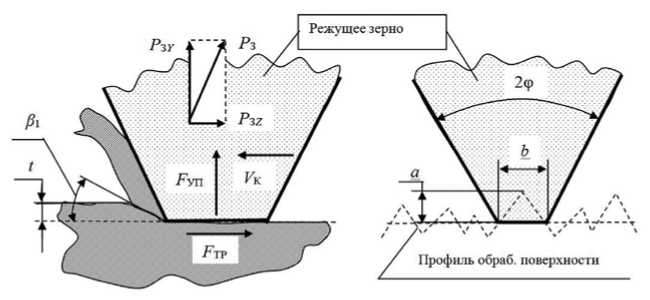
Рис. 3. Схема сил, действующих на режущее зерно

При моделировании динамики процесса резания при шлифовании процесс резания будем отображать в виде полной линейной модели [68], так как процесс микрорезания зерна соответствует процессу резания резцом. При этом процессы микрорезания зерен, находящихся в контакте с заготовкой, представим в виде некоторого совокупного процесса

P + — p = hpxx + kpyy + НруУ + kpzZ + hpzz, TP где kPx, kPy – коэффициенты резания по осям x иy; hPx, hPy , hPz – коэффициенты демпфирования по координатам x, y, z.

Коэффициенты резания по осям y и z при шлифовании можно вычислить по следующим выражениям:

где a – глубина микрорезания единичным абразивным зерном; в - угол между равнодействующей силы резания и скоростью резания; в , — угол сдвига; т - среднее касательное напряжение в плоскости сдвига; n _р – фактическое число зерен, участвующих в резании на единице площадки контакта круга с заготовкой; B – ширина контакта круга с заготовкой; l _д – длина контакта круга с заготовкой.

Величину фактического числа зерен, участвующих в резании на единичной площадке контакта круга с заготовкой можно определить исходя из законов теории вероятности по выражению [9]:

₍ = 0,4     № * • K *

Р   xс2р Vuк • (1 -е),

kPy =

' 3,25 • sin p   )

• _R-----⁺¹ ^ n p • B • ^l д , ^     Sin P 1        J

где x _ср - средняя величина зерна, мм; K * - кон

^k Pz

73,25 • cos P   ) _D ,

[    Sin P ,     ⁺7" n p • B • ^l Д '

центрация режущего материала в круге, %; и _к -скорость шлифования, м/с; £ - относительная глубина заделки зерен, (е~0,7-0,8); ® * - скорость погружения зерен в обрабатываемый материал, мм/с.

В данной модели учитывается жесткость и демпфирование по ортогональным координатам z , y , которые определяют величину сечения срезаемого слоя материала. По координате x учитывается только демпфирование резания. В левой части уравнения отражена инерционность процесса резания. Несмотря на то, что постоянные времени процесса резания при шлифовании не велики, намного меньше, чем при обработке лезвийным инструментом, мы пытаемся в модели учесть их влияния. Итоговые потоки тепла определяем как результат совокупности элементарных потоков, соединенных параллельно. Элементарные источники представим аналогично в виде соответствующих совокупных источников.

Q = q • n д • l д • B ,                 (5)

где n _д – средневероятное количество режущих зерен, активно участвующих в процессе шлифо вания на единице контакта ; l_д – длина контакта ; B – ширина контакта.

Математическая модель термодинамической системы установки для абразивной обработки теплозащитного покрытия представляет собой систему обыкновенных дифференциальных уравнений с постоянными коэффициентами:

M z z + hz + C_zz + k_zP = 0 ,

M x x + h x x + C x x + k _x P = 0 ,

M y y + h_yy + С у У + k y P = 0 ,

^h Px x ^{+ h} Py y ^{+ k} Py y ^{+ h} Pz z ^{+ k} Pz z ⁺ — P ⁺ P = ⁰ , T _P

к

Сстр d61 + 1 —+ — 6

—

к

(

R R стр тп 7

к

1- 6+1—+-|a тп

к Rтп  Rz 7

—

—

1- 6 2 = Q Д b , R тп

—    6 3 = Q тп ,

R _Z

к

—6₂ + c _p d^ + —+—+— 6

R ^{2 р} ^ У У У ³

—

Z

dt

к

R

p

к

R

Y

R

-^Z 7

6₄ = 0 ,

^RY ⁴

1- 63 +1 — + — |6

R _Y

к R Y    ^R _T3 _y

„  ⁶ 5 = ^Q ТЗ ’

R ТЗ

—

Т" ⁶ 4 ^{+ С} И    + !/?+/?   ⁶ 5 = ^Q ^ ^{(1 —} b )

R тз         at    к R тз    R и 7

где 6 i - средние температуры в узловых точках эквивалентной схемы; k Py , k Pz – коэффициенты резания по соответствующим координатам; h Px , h Py , h Pz – коэффициенты демпфирования резания по соответствующим координатам; k x , k y , k z – коэффициенты, определяемые проекциями силы резания на соответствующие оси. Обозначения остальных параметров, входящих в выражения (6), приведены ниже.

Используя метод электротепловой аналогии и метод узловых потенциалов, можно составить эквивалентную схему термодинамической системы установки для абразивной обработки теплозащитного покрытия (рис. 4).

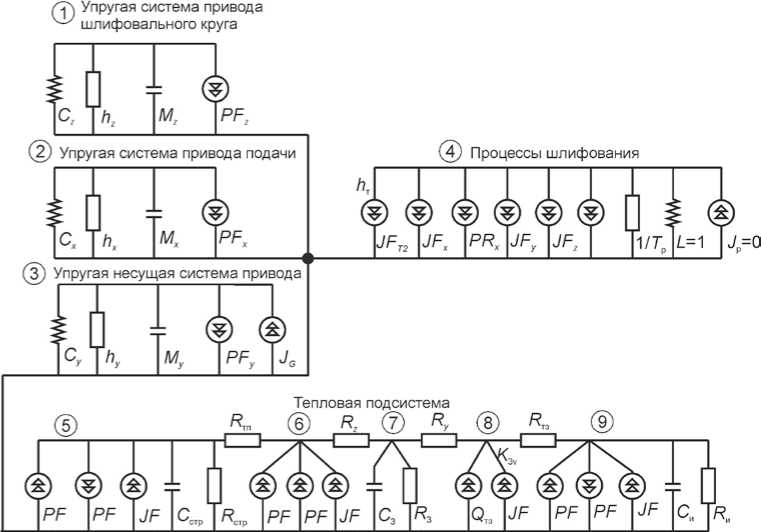
Рис. 4. Эквивалентная электротепловая схема замещения термодинамической системы установки для абразивной обработки теплозащитного покрытия

где C z ,C x , C y – приведенные жесткости соответствующих подсистем, h z ,h x, h y – приведенные коэффициенты демпфирования механических подсистем; M z , M x , M y, J G – приведенные инерционные параметры подсистем, L – условная податливость процесса резания единичной величины; T p – постоянная времени стружкообразования; J p – номинальная сила резания, определяемая припуском; . Q ТЗ – источник тепла от трения по задней поверхности зерен; PF, JF - фиктивные источники, отражающие взаимодействие подсистем. C и , C стр и С з – емкостные элементы, учитывающие теплоемкость соответствующих участков и определяемые удельной теплоемкостью материалов и размерами рассматриваемых участков (изделие, стружка,зерно); R стр , R тп , R у , R z , R тз, R и , R з – резистивные элементы, отражающие теплопроводность участков: R тп отражает теплообмен между стружкой и передней поверхностью резца, R тз – между обрабатываемой поверхностью и задней поверхностью резца, R стр отражает отвод тепла со стружкой из зоны резания, R и учитывает теплоотвод из зоны резания в глубину изделия, элементы R у и R z отражают теплообмен между задней и передней поверхностями зерна, R з – теплоотвод в связку круга.

Выводы: на основании предложенной модели были рассчитаны зависимости температуры и сил резания от механических свойств теплозащитного покрытия, скорости шлифования и скорости детали, величины зерна абразивного круга и его коэффициента затупления, коэффициента трения на контактной поверхности абразивного инструмента и обрабатываемого материала.

Сопоставление расчетных данных и результатов проведенных экспериментов свидетельствует о целесообразности использования разработанной модели для повышения эффективности технологического процесса абразивной обработки теплозащитных покрытий, а также для повышения качества обрабатываемой поверхности.