Моделирование процесса измерения корпусных деталей на координатно-измерительной машине

Наиболее часто операторы проводят процесс измерения методом сканирования. Траекторией движения измерительной головки (ИГ) является кривая и в результате контроля измеряется несколько сотен точек. Подобный метод является самым точным среди контактных методов измерения, однако с увеличением количества контролируемых точек повышается время контроля. Точность измерения промышленных КИМ, не предназначенных для прецизионных измерений, варьируется от 3 мкм до 1,8 мкм и точнее. Как правило, точность КИМ в десяток раз превосходит контролируемые значения допусков. Следовательно, в процессе измерения будет достаточно пользоваться контактным методом, сократив тем самым время контроля [1].

В работе изучено влияние стратегии измерения при контроле длинны корпусной детали на точность измерения. Замеры проводились контактным методом. Измерения проводились на КИМ Contura фирмы Carl Zeiss с измерительной системой RDS. В качестве измеряемого образца была выбрана деталь, представленная на рис.1. В качестве измеряемого параметра выбрана ширина детали (размер длины между поверхностями 1 и 2). Ширина детали измерялась по следующим стратегиям: расстояние между точкой на плоскости и противоположной плоскостью измеренной по 4 точкам (т-пл4); расстояние между т-пл6; расстояние между т-пл8; расстояние между пл4-пл4; расстояние между пл6-пл6; расстояние между пл8-пл8.

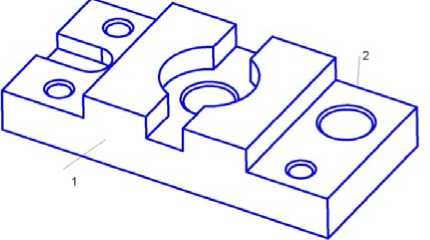
Рис. 1. Рабочая деталь

формы будем считать отклонение от плоскостности. Приняв погрешность ощупывающей головки ∆ КИМ =4,78 мкм; погрешность формы: ∆ ф1 =4 мкм для поверхности 1 и ∆ ф2 =2 мкм для поверхности 2, получим, что ширина зоны разброса для каждой стороны составит:

∆ 1 = ∆ КИМ + ∆ ф1 = 4 + 4,78 = 8,78 мкм;

∆ 2 = ∆ КИМ + ∆ ф2 = 2 + 4,78 = 6,78 мкм;

Из рис. 2 видно, что размах значений, будет равен:

При разработке математической модели оптимизации процесса измерения за основу была взята модель прогнозирования погрешности измерения концевых мер длинны [2-4]. Суть модели заключается в том, что взаимосвязь между параметром точности и количеством измеряемых точек будет выражаться через величину размаха с учетом влияния погрешностей при измерении. Теоретически с каждой стороны измеряемой детали имеется зона (разброс точек) шириной равной ∆, которая обуславливается погрешностью измерительной головки и погрешностью формы детали. В эту зону попадают точки измерения. При измерении расстояния между поверхностями по методу от точки на одной поверхности до точки расположенной на другой, ширина разброса с каждой стороны будет равна ∆ (рис. 2). Если использовать метод аппроксимации поверхностей в плоскости, и измерять расстояние между плоскостями, тогда зона разброса точек усредняется и сужается на величину n , где n – количество точек измеренных на плоскости, соответственна она будет равна Д/Vn с каждой стороны (рис. 2).

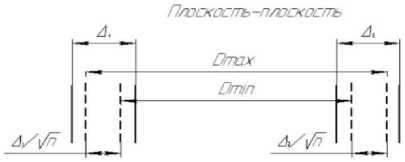
Рис. 2. Графическое представление процесса измерения

Ширина зоны разброса ∆ будет складываться из погрешности ощупывающей головки и погрешности формы измеряемых поверхностей детали. Так как измерение будет проходить между плоскостями, в качестве погрешности

RТП = Dmax - D min Л    A 2 = А1 + “/=; n Rnn =D -D = ^L + А^ ПП max min nn где RТП – размах по точке и плоскости; RПП – размах по двум плоскостям; n – количество точек на плоскости.

Подставляя значения ∆ 1 и ∆ 2 в выражения разма-хов рассчитывается значения R ТП и R ПП . Данные о полученных величинах размаха представлены в табл. 1. По данным табл. 1 строится диаграмма (рис. 3).

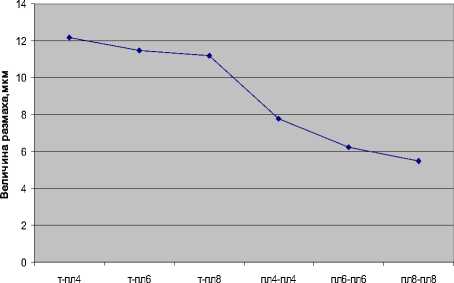
Метод измерения

Рис. 3. Диаграмма распределения размаха

Согласно полученным результатам математическая модель отражает зависимость между методом измерения и величиной размаха. Из рисунка видно, что минимальная величина размаха соответствует методу измерения – пл8 - пл8. Это обуславливается тем, что уменьшается величина разброса из-за более точной аппроксимации поверхностей. Эксперимент проводился при заданной степени уверенности Р=0,95%, таким образом количество замеров для одной стратегии равняется n=10. Базирование детали осуществлялось по трем перпендикулярным плоскостям. Графическое представление процесса измерения выполнено в системе «ТехноКорд» и представлено на рис. 4. Результаты экспериментов представлены в табл. 2.

Таблица 1. Данные величин размаха

Размах	Метод измерения
	т-пл4	т-пл6	т-пл8	пл4-пл4	пл6-пл6	пл8-пл8
R, мкм	12,17	11,49	11,18	7,78	6,22	5,50

Согласно полученным результатам математическая модель отражает зависимость между методом измерения и величиной размаха. Из рисунка видно, что минимальная величина размаха соответствует методу измерения – пл8 - пл8. Это обуславливается тем, что уменьшается величина разброса из-за более точной аппроксимации поверхностей. Эксперимент проводился при заданной степени уверенности Р=0,95%, таким образом количество замеров для одной стратегии равняется n=10. Базирование детали осуществлялось по трем перпендикулярным плоскостям. Графическое представление процесса измерения выполнено в системе «ТехноКорд» и представлено на рис. 4. Результаты экспериментов представлены в табл. 2.

Из анализа табл. 2 следует, что минимальная величина размаха соответствует методу измерения – от плоскости до плоскости по 8 точкам. Максимальная величина размаха соответствует методу измерения от точки до плоскости, измеренной по 4 точкам. Данные полученные в ходе моделирования и в ходе экспериментального исследования сопоставлены в табл. 3. Анализ табл. 3 показывает, что математическая модель не противоречит данным эксперимента и отражает характер поведения величины размаха. Расхождение данных модели с данными, полученными экспериментальным путем не превышают 17%.

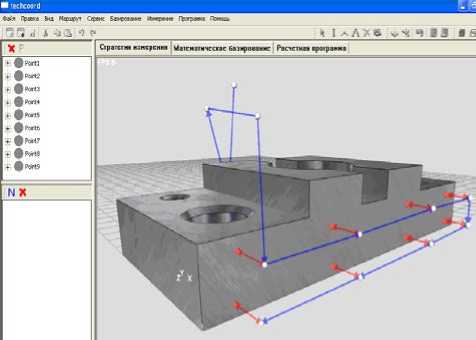
Рис. 4. Схема измерения т-пл8

Установлено, что процесс измерения от плоскости до плоскости по восьми точкам является наиболее точным, так как аппроксимация плоскостей происходит с двух сторон измеряемой детали. Это говорит о том, что вероятность события, когда какая либо точка, попадая во впадину или выступ, влияет на процесс измерения, снижается, так как средняя плоскость будет строиться из заданного условия аппроксимации по всему набору измеренных точек. Таким образом, процедура контроля корпусных деталей состоит из следующих этапов:

Таблица 2. Результаты экспериментов

Параметр	Значение диаметра D,мм
	т-пл4	т-пл6	т-пл8	пл4-л4	пл6-л6	пл8-л8
Dmax ,мм	58,0257	58,0240	58,0131	58,0348	58,0080	57,9999
Dmin ,мм	58,0111	58,0097	57,9992	58,0260	58,0009	57,9936
R ,мм	0,0146	0,0143	0,0139	0,0088	0,0071	0,0063

Таблица 3. Данные моделирования

Размах	Метод измерения
	т-пл4	т-пл6	т-пл8	пл4-пл4	пл6-пл6	пл8-пл8
R теор , мкм	12,17	11,49	11,18	7,78	6,22	5,50
R экспер , мкм	14,60	14,30	13,90	8,80	7,10	6,30
Расхождение %	17	11	10	11	12	12

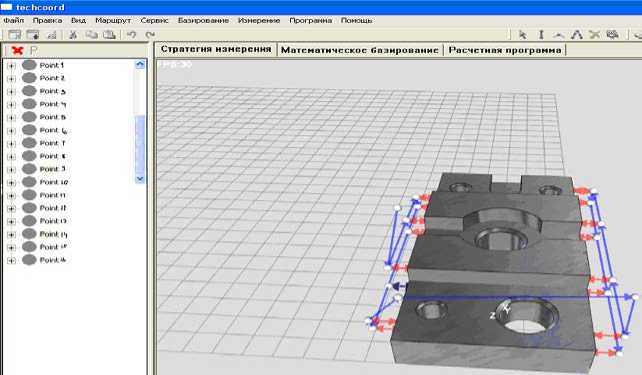
Рис. 5. Измерение по схеме пл8 – пл8

• 1.    Установка детали на стол КИМ.

• 2.    Математическое базирование детали.

• 3.    Написание управляющей программы для стратегии измерения пл8-пл8:

• 3.    Измерение длинновых размеров. Алгоритм измерения представлен на рис. 5.

• 4.    Распечатка протокола контроля.

Plane plane1 = Average. Plane (Point1, Point2, Point3, Point4, Point5, Point6, Point7, Point8);

Plane plane2 = Average. Plane (Poin9, Point10, Point11, Point12, Point13, Point14, Point15, Point16);

Number d1 = Distance. PlanePlane (plane1, plane2);