Моделирование процесса охлаждения элементов радиоэлектронной аппаратуры в SolidWorks
Автор: Соловьв Аркадий Николаевич, Глазунова Лейла Владимировна
Журнал: Advanced Engineering Research (Rostov-on-Don) @vestnik-donstu
Рубрика: Физико-математические науки
Статья в выпуске: 4 (47) т.10, 2010 года.
Бесплатный доступ
С увеличением интеграции современной радиоэлектронной аппаратуры (РЭА) существенно возрастает и трудоемкость ее проектирования, что связано с ростом размерности задач, решаемых в процессе разработки. Эффективным способом решения этой проблемы является применение системы автоматизированного проектирования SolidWorks. В работе с помощью этой системы решается задача расчета параметров радиатора охлаждения для бесперебойной работы одного из элементов РЭА.
Моделирование процесса охлаждения, тепловыделяющие элементы, теплоотдача, метод конечных элементов (мкэ)
Короткий адрес: https://sciup.org/14249382
IDR: 14249382 | УДК: 004.414.23:62-714:621.37
Текст научной статьи Моделирование процесса охлаждения элементов радиоэлектронной аппаратуры в SolidWorks
В расчетном модуле SolidWorks Flow Simulation необходимо задать условия задачи, максимально приближенные к реальным условиям эксплуатации, провести расчеты и интерпретацию полученных результатов.
В основе расчетной методики лежит, во-первых, математическая модель рассчитываемых физических процессов и, во-вторых, способ решения поставленной математической задачи.
Математические модели конкретной инженерной задачи представляют собой начальнокраевые задачи, отражающих законы физики и механики с привлечением полуэмпирических и эмпирических констант и зависимостей.
Движение и теплообмен в жидкости и газе моделируется с помощью уравнений Навье– Стокса [3], описывающих законы сохранения массы, импульса и энергии этих сред. Эта система уравнений нестационарного пространственного течения имеет следующий вид в рамках подхода Эйлера в декартовой системе координат (хi, i = 1, 2, 3):
где
Уравнение состояния газообразной среды:
P = р ( р , T , У )
У = ( У 1 , У 2 >—> Уп ) — вектор концентраций компонентов среды.
Уравнение состояния жидкости:
P = P( т , У ) .
Тензор вязких сдвиговых напряжений определяется следующим образом:
т
дu дuj j=P + дx, дх,.
V j i
—
2 д u i
-
2 -j 5
-
3 д x i
\
ij
— 3 р к 5 ij ,
где
ц = ц i + ц d , — коэффициент динамической вязкости ц d ; ц t — коэффициент турбулентной вязкости; 5 ik — дельта-функция Кронекера; к — кинетическая энергия турбулентности.
Диффузионный тепловой поток моделируется с помощью уравнения qk =
—
г >
P i , P t 1
Р п
V r 0 c 7
д T 7 1 т т
Ср —, к = 1,2,3 , дxk
где о С = 0,9 , P r — число Прандтля; c P — удельная теплоемкость при постоянном давлении; T — температура среды.
Теплопередача в твердых телах рассчитывается с помощью уравнения [4]: др cT д Г. д T ) _
= х^ + Q H - (8)
дt дxi V дxi J где С — удельная теплоемкость; T — температура; X — теплопроводность.
Радиационный теплообмен моделируется в соответствии с законом Стефана — Больцмана:
Q h =80 0 ( T W — T S ) ,
где е — степень черноты поверхности; о — постоянная Стефана—Больцмана; TW — температура поверхности, испускающей излучение; TS — температура окружающей среды.
Поскольку используемые в математической модели системы дифференциальных уравнений не имеют аналитического решения, они приводятся к дискретному виду и решаются на некоторой расчетной сетке.
Моделирование в SolidWorks. В системе SolidWorks (Договор № И05110-77 от 05.11.2009 г.)строим объемную модель корпуса и радиатора (рис.1). Для проведения расчета модель блока упрощаем в силу лимитированности вычислительных ресурсов: заменяем элементы сложной геометрии более простыми, исключаем элементы, влиянием на результаты расчета которых можно пренебречь. Выполняем две заглушки в радиаторе жидкостного радиатора, «герметизирующие» полость каналов внутри радиатора, и две заглушки на корпусе блока. Это сделано для того, чтобы сформировать подобласть, занятую охлаждающей жидкостью, в первом случае, и подобласть, заполненную воздухом, во втором случае. Условия входа и выхода теплоносителей должны быть приложены к внутренним сторонам заглушек.
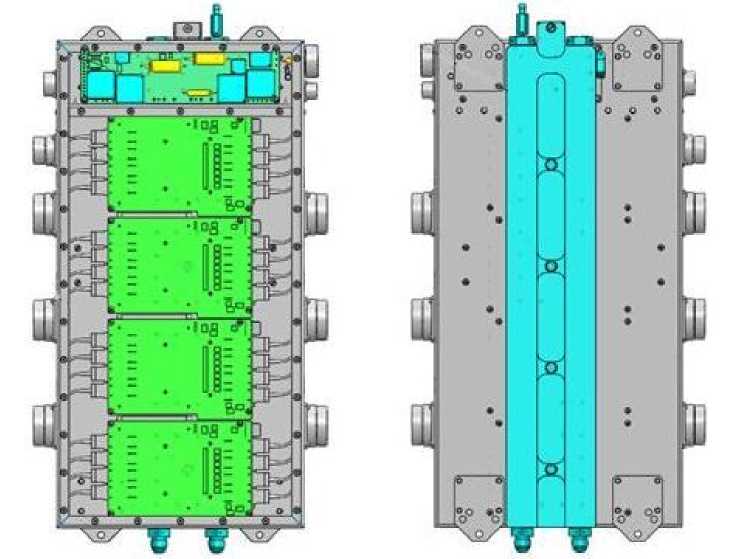
а)
б)
Рис.1. Блок обработки приемного сигнала: а – вид спереди; б – вид сзади (на виде спереди крышка скрыта)
Конструкция блока (рис.2) включает в себя корпус 3 , тепловыделяющие элементы, крепления, пластинчатые радиаторы между корпусом и тепловыделяющими элементами. Тепловыделяющими элементами являются микросхемы. Две микросхемы 1 входят в состав модуля электропитания VICOR V24C5T50BL3 с тепловыделением 7,5 Вт каждая и располагаются между платой модуля и пластинчатым радиатором. Четыре микросхемы 2 , мощностью 25 Вт каждая, входят в состав устройства управления и цифровой обработки. Вся конструкция изготовлена преимущественно из алюминиевого сплава АМг5, за исключением плат из стеклотекстолита. Радиатор охлаждения примыкает ко дну корпуса блока. Блок проектируем таким образом, чтобы тепловыделяющие элементы плотно прилегали к пластинчатым радиаторам, отводящим тепло к корпусу блока. А затем от корпуса блока тепло передается общему радиатору жидкостного охлаждения. Жидкость, в качестве которой выбран водный раствор этиленгликоля ОЖ-65, циркулирует по П-образному каналу круглого сечения диаметром 10 мм. Температура охлаждающей жидкости на входе в канал равна +35±5 ºС, расход – 1 л/мин. Задачей охлаждения является обеспечение отвода тепла с теплонагруженных элементов на несущую конструкцию, а затем осуществление конвективной теплопередачи между конструкцией и теплоносителем.
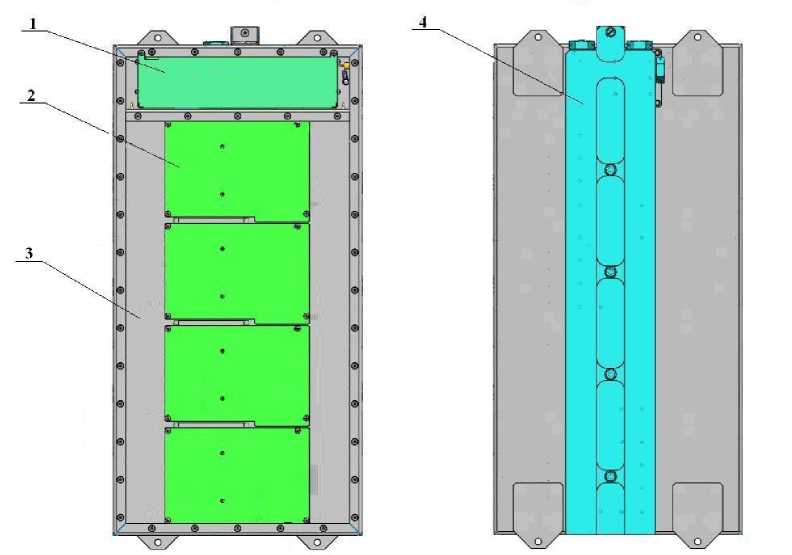
а) б)
Рис.2. Модель блока для расчета:
а – вид спереди; б – вид сзади (на виде спереди крышка скрыта)
Деградационные процессы при пониженной температуре, связанные с конденсацией влаги, изменением электрических характеристик, деформаций сопряженных деталей, в расчетах не рассматриваются вследствие ограниченных возможностей программы. В расчете рассмотрен случай, соответствующий наибольшей вероятности появления перегрева, при котором температура окружающего воздуха +65 ºС.
Для адаптации математической модели к конкретной физической задаче и области пространства задаем условия задачи.
Граничные условия: температура блока - + 65 °С, температура окружающего воздуха - + 65 °С. Назначены две текучие среды: внутри блока: воздух и теплоноситель ОЖ-65 (в каналах радиатора). Условие входа охлаждающей жидкости в канал радиатора: температура жидкости - + 40 °С и скорость жидкости - 0,213 м/с. Условие выхода охлаждающей жидкости: статическое давление. На стенках блока — теплоотдача наружных стенок блока с учетом окружающей температуры, статическое давление - на боковой стенке блока (имитация негерметичности блока).
Назначены коэффициенты излучения и степень черноты элементов конструкции, массовый расход, шероховатость поверхности каналов радиатора, мощность термоактивных элементов по условию задачи. Создана модель контактного теплового сопротивления между термоактивными элементами и корпусом блока, соответствующего защитному покрытию корпуса блока, применяемому в связи с повышенной влажностью окружающей среды. Также активизирована опция «Давление в точке отсчета», при которой статическое давление жидкой среды автоматически корректируется по высоте с учетом гравитационного ускорения.
Для нахождения искомого численного решения задачи континуальная математическая модель физических процессов дискретизируется по пространству. Решение задачи о движении и теплообмене жидкой среды и газа определяется как установившееся во времени. Исходя из условия Куранта [5], шаги дискретизации по пространству в ячейке определяются в зависимости от значений физических величин. На сформированной таким образом некоторой расчетной сетке дискретное решение поставленной дифференциальной математической задачи в общем случае зависит от размеров ячеек расчетной сетки. Для дискретизации дифференциальных уравнений в SolidWorks Flow Simulation используется метод конечных объемов. Чтобы решить поставленную математическую задачу с заданной точностью, необходимо провести несколько расчетов на разных более редких и более частых расчетных сетках, чтобы определить такую частоту сетки, начиная с которой решение задачи перестает значимо зависеть от частоты сетки, что указывает на достижение необходимой точности решения математической задачи, т.е. сеточной сходимости решения математической задачи. Таким образом, допустимый уровень разрешения сеткой выступов поверхности задаем максимальным. Включаем опцию дробления сетки в узких каналах и устанавливаем критическое число ячеек поперек узкого канала, равное 11. Минимальный размер ячеек - 0,123 мм, минимальная толщина стенок твердого тела- 0,7 мм.
Численные результаты. Решение системы уравнений (1)-(3) для стационарных процессов зависит от следующих условий:
-
- физические условия, характеризующие теплофизические свойства среды: с р , р , X , в , ц , ц i ;
-
- геометрические условия, определяющие форму и размеры системы, в которой протекает процесс;
-
- граничные условия, определяющие взаимодействие между различными средами на внешних и внутренних границах рассматриваемой системы.
Варьируя эти условия, можно повлиять на параметры теплового процесса.
Расчет показал, что при пониженном атмосферном давлении и повышенной температуре окружающего воздуха излучение тепла с теплонагруженных элементов в воздух по сравнению с нормальными условиями эксплуатации снижается на 17,8 %, а конвекция с воздухом - на 9 %, так как уменьшается теплоемкость воздуха. Таким образом, наибольший отвод тепла осуществлен радиатором жидкостного охлаждения. Температура микросхем не превышает допустимую и равна +52 °С (рис.3), что ниже допустимого значения на 18 °С; температура плат - 54 °С; температура воздуха внутри блока - 63,8 °С (рис.4,а); температура жидкости на выходе из радиатора повысилась на 0,4 ºС (рис.4,б). Это позволяет прогнозировать надежную работу блока. Эффективное
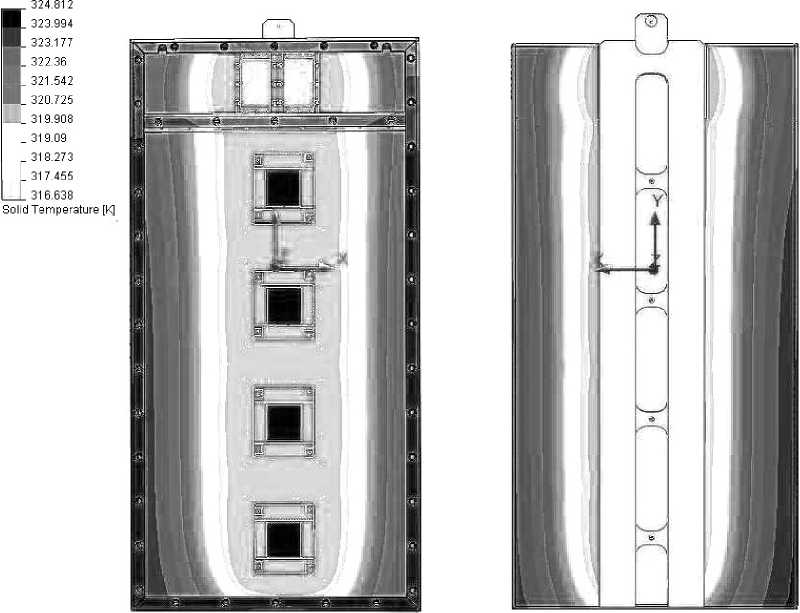
Рис.3. Распределение температуры в блоке: а – вид спереди; б – вид сзади (крышка и платы скрыты)
охлаждение обусловлено оптимальным сочетанием следующих свойств охлаждающей жидкости, величины которых входят в уравнения (1)-(6): коэффициент динамической вязкости, коэффициент турбулентной вязкости, скоростной напор, плотность, теплоемкость.
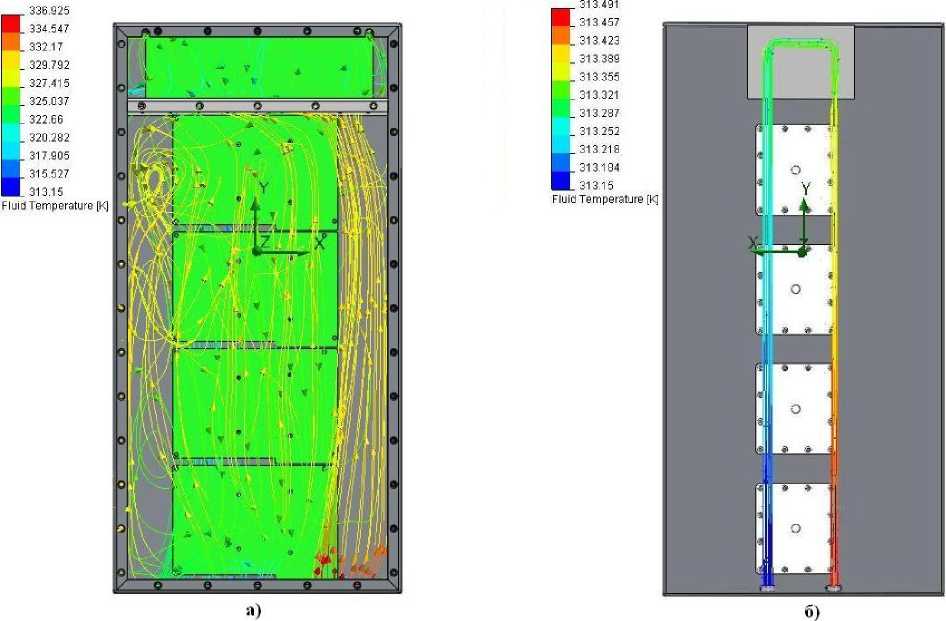
Рис.4. Температура воздуха в блоке и потока жидкости в радиаторе охлаждения: а – вид спереди; б – вид сзади (радиатор скрыт для визуализации результатов)
Если варьирование физическими и граничными условиями невозможно, можно изменить, во-первых, геометрию канала и, во-вторых, поверхность съема тепла.
В первом случае при сужении диаметра канала от 11 до 2 мм происходит интенсификация теплоотдачи, обусловленная повышением турбулизации пограничного слоя охлаждающей жидкости вследствие увеличения скорости ее течения. При диаметре меньше 2 мм происходит уменьшение теплоотдачи, вызванное сокращением площади съема тепла (см. табл.). При увеличении диаметра канала более 13 мм теплоотдача снижается в результате снижения скорости течения. При любом из диаметров канала рассматриваемого диапазона теплоотдача эффективна.
Зависимость параметров теплового процесса от диаметра канала
|
Диаметр канала радиатора, мм |
Температура жидкости на выходе из канала, ºС |
Минимальная температура кристалла, ºС |
Максимальная температура кристалла, ºС |
Скорость течения охлаждающей жидкости, м/с |
Отведенная радиатором тепловая мощность, Вт |
|
2 |
40,2 |
48,5 |
55,4 |
5,3 |
82,1 |
|
4 |
40,1 |
48,0 |
54,5 |
1,327 |
81,29 |
|
6 |
40,15 |
48,6 |
55,1 |
0,589 |
79,92 |
|
8 |
40,25 |
51,3 |
55,9 |
0,332 |
78,02 |
|
10 |
40,35 |
51,7 |
56,9 |
0,212 |
76,39 |
|
11 |
40,4 |
52,1 |
57 |
0,175 |
75,38 |
|
13 |
40,3 |
53,7 |
57,3 |
0,126 |
76,57 |
|
15 |
40,45 |
49,4 |
55,9 |
0,094 |
76,51 |
Во втором случае на теплоотдачу влияет шероховатость поверхности каналов радиатора. Причина в том, что вблизи шероховатой стенки скорость потока уменьшается больше, чем вблизи гладкой, что приводит к уменьшению теплового потока на 10 %. Наличие же шероховатости, по крайней мере, в модели SolidWorks Flow Simulation, никак не сказывается на излучающих свойствах поверхностей.
Выводы . Результат расчета показывает наличие в блоке дополнительных напряжений термического происхождения. Величина максимального напряжения составила 1972 Па. Термостойкость должны повышать все факторы, уменьшающие величину деформации при термических нагрузках, в первую очередь, снижение коэффициента термического расширения и увеличение теплопроводности. Следовательно, для снижения напряжений в конструкции необходимо увеличить толщину деталей, а также заменить материал конструкции на более термостойкий, например, АМг6.
Перспектива продолжения работы состоит в решении вопроса о взаимном действии механических и тепловых эксплуатационных нагрузок и подтверждении результатов расчетов экспериментальной проверкой.
Список литературы Моделирование процесса охлаждения элементов радиоэлектронной аппаратуры в SolidWorks
- Дульнев Г.Н. Тепловые режимы радиоэлектронной аппаратуры/Г.Н. Дульнев, Н.Н. Тарановский. -Л.: Энергия, 1971.
- Справочник конструктора РЭА. Общие принципы конструирования/под ред. Р.Г. Варламова. -М.: Советское радио, 1980.
- Исаченко В.П. Теплопередача/В.П. Исаченко, В.А. Осипова, А.С. Сукомел. -М.: Энергия, 1981. -417 с.
- Михеев М.А. Основы теплопередачи/М.А. Михеев, И.М. Михеева. -М.: Энергия, 1977. -343 с.
- Галлагер Р. Метод конечных элементов. Основы/Р. Галлагер; пер. с англ. -М.: Мир, 1984.
- Dul'nev G.N. Teplovye rejimy radioelektronnoi apparatury/G.N. Dul'nev, N.N. Taranovskii. -L.: Energiya, 1971. -in Russian.
- Spravochnik konstruktora REA. Obschie principy konstruirovaniya/pod red. R.G. Varlamova. -M.: Sovetskoe radio, 1980. -in Russian.
- Isachenko V.P. Teploperedacha/V.P. Isachenko, V.A. Osipova, A.S. Sukomel. -M.: Energiya, 1981. -417 s. -in Russian.
- Miheev M.A. Osnovy teploperedachi/M.A. Miheev, I.M. Miheeva. -M.: Energiya, 1977. -343 s. -in Russian.
- Gallager R. Metod konechnyh elementov. Osnovy/R. Gallager; per. s angl. -M.: Mir, 1984. -in Russian.


