Моделирование процесса отделения крышки узлов подвески от возвращаемого аппарата с учётом упругих свойств вытяжного блока

Одним из этапов ввода парашютной системы (ПС) пилотируемого транспортного корабля (ПТК) является ввод вытяжного парашюта (ВП) в рабочем диапазоне скоростных напоров (рис. 1). После отстрела крышки узлов подвески (КУП) в поток вводится вытяжной блок (ВБ) с ВП. ВБ связан с КУП уздечкой, а внутри ВБ уложено звено ВП [1], которое вытягивается из ВБ при его движении. При полной выработке звена ВП из ВБ происходит ввод ВП (рис. 2).

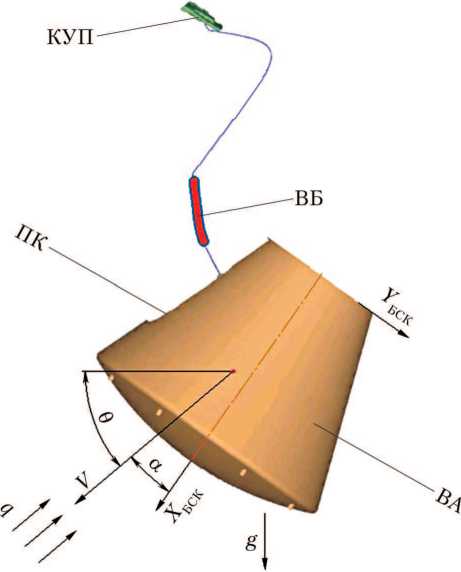
Рис. 1. Схема ввода вытяжного парашюта: КУП — крышка узлов подвески; ВБ — вытяжной блок; ПК — парашютный контейнер; ВА — возвращаемый аппарат; q — скоростной напор; V — скорость аппарата; g — ускорение свободного падения; 6 — угол наклона траектории; а — угол атаки; X БСК и Y БСК — оси базовой системы координат (рисунок создан автором)

Рис. 2. Вытяжной блок с вытяжным парашютом: m — масса вытяжного блока (рисунок создан автором)

Динамика движения КУП после отстрела с учётом аэродинамической интерференции от возвращаемого аппарата (ВА) исследовалась в работах [2–5]. Основным инструментом исследования являлся программный комплекс FlowVision , позволяющий осуществлять на каждом шаге интегрирования расчёт аэродинамического воздействия на КУП и ВА методом конечных объёмов с применением динамической сетки, где моделируется течение вязкого сжимаемого газа с использованием осреднённых по Рейнольдсу уравнений Навье – Стокса и k е -модели турбулентности [6—9].

Анализ результатов проведённых расчётов позволил выявить потенциальную возможность раскрутки автономно двигающейся КУП в потоке до угловых скоростей более 2 000 ° /с, создавая риск наматывания ВП на КУП, что может привести к отказу ввода ПС.

Постановка задачи

Очевидна необходимость создания динамической модели процесса отделения, которая позволит учитывать взаимодействие ВБ и КУП и оценить его влияние на угловую скорость КУП. ВБ, связанный с КУП и ВА, оказывает влияние на движение КУП, в т. ч. на участке ударного взаимодействия при выдёргивании ВБ из парашютного контейнера, и определяет положение КУП в момент полного вытягивания звена ВП и его раскрытия в потоке.

В связи с этим, целью настоящей работы является разработка адекватной модели ВБ, отражающей физический процесс, которую впоследствии можно будет использовать в составе динамической модели процесса отделения КУП от ВА.

К основным задачам исследования можно отнести разработку методики подбора параметров модели ВБ и методики её валидации.

ВБ представляет собой чехол с плотно уложенным внутри ВП и звеном ПС, связывающим вытяжной и тормозной парашюты. Известны массово-инерционные характеристики ВБ и его геометрия в исходном состоянии в начальный момент времени. В результате проведённых экспериментов было установлено, что сила, выдёргивающая ВБ из парашютного контейнера, существенно деформирует ВБ.

В настоящей статье рассмотрен процесс создания и валидации модели ВБ с учётом изгибных и крутильных деформаций ВБ на основе экспериментальных данных , полученных при отстрелах имитатора КУП, который соединён с ВБ через уздечку.

Модель вытяжного блока

Рассматривается возможность моделирования ВБ в виде динамической системы, представляющей из себя совокупность отдельных твёрдых тел (звеньев), соединённых вязкоупругими пружинами, которые обеспечивают взаимодействие между звеньями системы (рис. 3).

Модель предполагает расчёт параметров движения каждого звена с учётом взаимодействия с соседними телами через пружины. Для адекватного моделирования динамики движения данной системы необходимо определить жёсткостные характеристики пружин, массы звеньев и коэффициенты демпфирования [10].

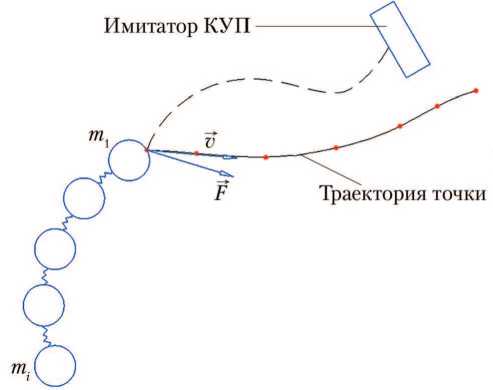
Рис. 3. Принципиальная схема модели вытяжного блока (ВБ): КУП — крышка узлов подвеса; m ₁ и m_i — маса 1-го и i-го тела соответственно; ^→ v — скорость точки подвеса ВБ; F — сила, действующая на точку подвеса ВБ (рисунок создан автором)

Центровочные и инерционные характеристики звеньев модели ВБ выбираются таким образом, чтобы суммарная масса звеньев соответствовала массе ВБ, моменты инерции жёстко скреплённых звеньев в начальный момент времени соответствовали моментам инерции недеформирован-ного ВБ.

Характеристики динамической модели ВБ определяются и корректируются на основании разработанной и описанной ниже методики, использующей данные, полученные при проведении наземной экспериментальной отработки.

Экспериментальная отработка

Рассмотрена серия отстрелов массового макета — имитатора КУП — на аэробаллистическом стенде. Экспериментальная установка (рис. 4) позволяет произвести отстрел имитатора КУП из ствола пускового устройства. Начальная скорость имитатора лежит в диапазоне штатных скоростей отстрела КУП. Проводилась видеофиксация отстрелов высокоскоростной камерой и измерялся профиль силы натяжения уздечки с помощью тензо-резисторного динамометра, установленного в разрыве уздечки.

Имитатор КУП, связанный уздечкой с ВБ, разрывает швартовку ВБ, и в процессе движения из ВБ вытягивается звено ВП.

По видеозаписям проведённого отстрела были созданы раскадровки (последовательности кадров с одинаковым шагом по времени). Время между соседними кадрами обратно пропорционально частоте съёмки видеокамеры. С использованием раскадровок создаётся кинограмма (рис. 5) и определяется траектория точки подвеса ВБ.

В неподвижной инерциальной системе координат в ОXY с началом в точке крепления уздечки к ВБ (на первом кадре раскадровки) определяются координаты и отмечаются реперами положения точек подвеса ВБ на каждом кадре в исследуемом диапазоне времени. Совокупность нанесённых реперов представляет из себя траекторию движения точки подвеса ВБ (рис. 6).

Координаты точки подвеса ВБ (таблица) приведены в инерциальной системе координат (рис. 6).

Рис. 4. Схема проведения испытаний по отстрелу имитатора крышки узлов подвески на аэробаллистическом стенде: 1 — пусковое устройство; 2 — стропа; 3 — вытяжной блок; 4 — динамометр; 5 — уздечка; 6 — имитатор крышки узлов подвески (рисунок создан автором)

0,0168 c                  0,0336 c                   0,0504 c                   0,0672 c

0,0840 c                       0,1008 c                       0,1176 c                     0,1344 c

Рис. 5. Кинограмма положений вытяжного блока при разгоне (рисунок создан автором)

Зависимость координат точки подвеса вытяжного блока от времени

Время, с	X , мм	Y , мм
0	0	0
0,0168	387	52
0,0336	628	51
0,0504	951	127
0,0672	1 338	299
0,0840	1 745	461
0,1008	2 120	637

Рис. 6. Траектория точки подвеса вытяжного блока с равным шагом по времени (рисунок создан автором)

По этому массиву координат методом сплайновой интерполяции находится дважды дифференцируемая функция (для возможности определения скорости и ускорения точки подвеса ВБ) перемещения точки подвеса ВБ от времени, предполагающая интерполяцию вне заданной сетки точек. Точки (рис. 6) должны быть соединены сплайнами таким образом, чтобы полученная функция соответствовала физическому процессу движения и исключала резкие изменения скоростей и ускорений на участках интерполяции. Наиболее близкие результаты интерполяции по указанным критериям для данной задачи даёт метод сплайновой интерполяции пятого порядка Акимы, который обеспечивает непрерывность самой функции и всех её производных до второй включительно.

В результате анализа функции определяются данные о координатах, скоростях и ускорениях точки подвеса ВБ, и появляется возможность интегрировать движение звеньев динамической системы, представляющих ВБ. Используя вышеперечисленные данные, можно решить обратную задачу динамики: определить силу, действующую на ВБ в точке подвеса. Ниже представлен алгоритм определения этой силы.

Подход к определению силы, действующей на точку подвеса вытяжного блока

Для

тел, на должны

расчёта динамики движения каждом шаге интегрирования быть вычислены главный

— вектор сил ∑Fk и

главный момент сил

—

∑Mk, которые состоят из векторной суммы всех действующих на тело сил и моментов соответственно.

В данной задаче в составе ∑ F_k и У M k появляются неизвестная сила F и момент этой силы M ( F ), вызывающие движение точки P подвеса ВБ по заданной траектории (рис. 7). _—

Значения внешней силы Fвн и её момента Мвн, являющиеся суперпозицией вязкоупругих силовых связей на i-е звено системы со стороны последующих звеньев, сил гравитации и аэродинамического воздействия, вычисляются на каждом шаге интегрирования.

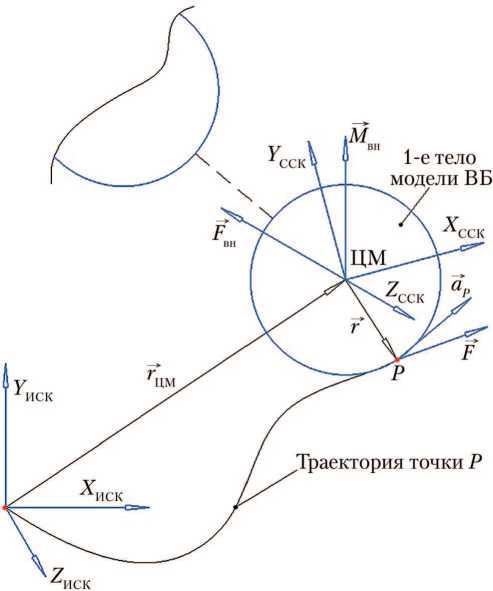
Рис. 7. Расчётная схема для первого тела модели: ВБ — вытяжной блок; ЦМ — центр масс; XИСК, YИСК, ZИСК — оси инерциальной системы координат; XССК, YССК, ZССК — оси связанной системы координат; →rЦМ — радиус-вектор из инерциальной системы координат в ЦМ объекта; →r — радиус-вектор из связанной системы координат в точку подвеса ВБ; F→вн — внешняя сила; M→вн — момент внешней силы; P — точка подвеса ВБ; F — сила, действующая на точку P; →aP — ускорение точки Р (рисунок создан автором)

Главный вектор сил Е F k и главный момент сил ∑ M_k , действующих на тело, можно раскрыть следующим образом:

^{—         —        —}                .

Е F_b = F + F = ma ; k         вн      ЦМ

_ ——        ^     ——         —— ——

Е Mb = M(F) + М = — X F + м , k                    вн                   вн’ где aЦМ — ускорение центра масс; m — масса i-го тела системы.

—

Формулу е = I ^-1 Е M_k - 1 ^-1[ —^— х ( I ^— )] можно раскрыть следующим образом:

^    .^      .

е = Г\г у- F) + I-1 Мвн -1-1[ю х (1ю)], где I–1 — обратный тензор инерции;

У — вектор углового ускорения.

Умножим каждое слагаемое векторно на г , обозначив известные члены как вектор Z :

^.       ^

_Sxr= [ I-\r x F )] X r + Z .               (1)

Ускорение точки P можно определить следующим образом: -         -            -         - >. - - ар = а ЦМ + ® х (® х г ) + е х г •

Выполнив необходимые преобразования, получаем:

—         —

F I е х r = - — ----- © х (ffl х r ) + a m m              P

Обозначим известные члены, являющиеся вектором, как вектор У :

——

F — е х r =--+ Y.

m

Из уравнений (1) и (2), введя вектор R, являющийся разностью векторов ( У - Z ), получаем следующее выражение:

r      F r

[ I-\r x F )] X г+ — = R .                (3)

Левую часть уравнения (3), являющуюся вектором, представим в матричном виде (условимся, что все проекции кинематических параметров будут приведены в осях системы координат, связанной с телом), что позволит представить данное выражение в виде произведения известной матрицы M на вектор неизвестной силы F :

__  ^r. ~     ^ ^F

[ I -\r x F )] X г+ ~

M 11 F x + M 12 F y + M 13 F z M ₂₁ F _x + M ₂₂ F _y + M ₂₃ F _z

M 31 F x + M 32 F y + M 33 F z

F x

= M ^. F ^y

F z

где M_{i, j} — соответствующий элемент матрицы M .

Тогда уравнение (3) принимает следующий вид:

M .

F x

_F ^y

F z

R x

R ^y

R z

Умножение обеих частей уравнения на обратную матрицу M ^–1 позволяет однозначно определить проекции на оси связанной си_стемы координат неизвестной силы F , вызывающей движение тела по заданной траектории:

F x		R x
F y	= M –1 .	R y
F z		R z

Моделирование процесса испытаний

В отечественном программном комплексе Euler реализован инструментарий, позволяющий смоделировать движение тела по известной траектории одной из его точек и определить силу, которая действует на данную точку.

В расчётах использовалась модель ВБ, состоящая из варьируемого количества тел, соединённых между собой вязкоупругими невесомыми пружинами, работающими на растяжение, сжатие и кручение. На рис. 8 представлен вариант такой модели, состоящей из пяти тел.

Настройка параметров модели ВБ производится в соответствии с разработанными критериями корректности модели ВБ. Суть основного критерия заключается в том, чтобы подобрать количество тел, коэффициенты продольной, крутильной жёсткости и демпфирования пружин таким образом, чтобы при покадровом сопоставлении координат, угловых положений звеньев компьютерной модели и соответствующих участков реального ВБ в процессе испытаний, данные параметры отличались в пределах заданной точности (рис. 9).

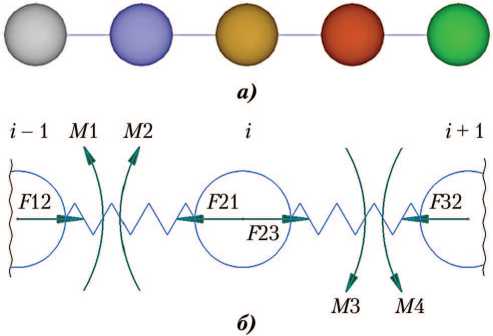
Рис. 8. Программная реализация вытяжного блока (ВБ): а — модель ВБ из пяти тел в программном комплексе Euler; б — принципиальная схема воздействия на i-ю массу ВБ со стороны соседних масс: M1, M2, M3, M4 — моменты, действующие на тела; F12, F21, F23, F32 — силы, действующие на тела (рисунок создан автором)

Дополнительным критерием корректности является сравнение профиля силы натяжения уздечки, измеренной тензо-резисторным датчиком при проведении эксперимента, и силы, вызывающей движение точки подвеса модели ВБ по траектории, определённой в программном комплексе Euler при компьютерном моделировании эксперимента.

Принимая во внимание тот факт, что ручной подбор характеристик модели ВБ — это трудоёмкая и затратная по времени задача, была написана программа на языке Python, позволяющая автоматизировать данный процесс. Программа позволяет многократно запускать расчёт динамики движения, изменяя значения жёсткости пружин и коэффициент демпфирования в требуемом диапазоне с заданным шагом изменения параметров.

Для поиска подходящих комбинаций параметров модели ВБ, удовлетворяющих вышеописанным критериям корректности, был написан ряд условий-флагов, отслеживающих некоторые промежуточные и конечные положения звеньев ВБ в пространстве. Координаты звеньев модели ВБ в этих положениях сравнивались с координатами соответствующих участков ВБ на видеозаписи эксперимента. При этом определялась степень совпадения силы, действующей на точку подвеса ВБ с данными эксперимента.

По результатам проведённых исследований по вышеописанной методике в качестве рабочей была выбрана

Рис. 9. Покадровое сопоставление положений модели вытяжного блока и видеозаписи проведённого эксперимента (см. рис. 5) (рисунок создан автором)

модель ВБ, состоящая из пяти тел с продольным коэффициентом жёсткости пружин с = 2,01·10⁴ Н/м, коэффициентом крутильной жёсткости пружин с кр = 5,28 Н-м/ ° и коэффициентом демпфирования k _д = 0,001 с.

Предполагается, что валидация модели ВБ будет осуществляться по вышеописанной методике с использованием результатов всех отстрелов имитатора КУП на аэробаллистическом стенде и предстоящих экспериментов.

Выводы

В статье рассмотрен один из критически важных этапов ввода ПС ПТК — процесс отделения КУП, от которого зависит успешность ввода ПС.

Для уточнения динамической модели процесса отделения КУП от ВА была разработана модель ВБ, позволяющая учитывать упругие свойства ВБ и его взаимодействие с КУП в процессе отделения.

По результатам анализа видеозаписей проведённой наземной экспериментальной отработки разработана методика по определению силы, действующей на точку подвеса ВБ.

Создана методика настройки модели ВБ на базе анализа видеозаписей проведённого эксперимента и показаний тензорезисторного динамометра.

Предполагается валидация разработанной модели ВБ по результатам предстоящих экспериментов и использование её в расчётах процесса отделения КУП от ВА.