Моделирование процесса разрушения сварных соединений

В обзоре экспериментальных работ [1] указывается, что одним из наиболее важных факторов, вызывающих разрушение сварных узлов (основного источника разрушения в машиностроительных конструкциях) является неизбежное наличие скрытых трещин или трещиноподобных дефектов. Проводится физико-техническая классификация процессов разрушения и обсуждение причин возникновения трещин в самом сварном шве, на границе раздела сред и в основном материале вне видимой при изготовлении конструкции зоны термического влияния. Кроме того, в работе [1] отмечаются проблемы построения аналитических моделей процесса разрушения в рамках линейной механики разрушения.

Исследование прочностных свойств сварных соединений проведено в работе [2], в которой применяется когезионная модель для достаточно общих параметров сварного соединения. В работе [3] даны оценки трещиностойкости границы раздела материалов. Отметим, что при использовании когезионной модели [2, 3] отсутствуют параметры, описывающие ширину сварного шва, поперечник зоны предразрушения и структуру самой зоны предразрушения. В экспериментальной работе [4], посвященной изучению распространения трещины нормального отрыва в биматериале керамика–алюминий, показано, что зона предразрушения для трещины на границе раздела сред, как правило, располагается только в одном, более слабом, материале (см. [4], Fig. 5) и локализуется в окрестности этой границы. Такое расслоение в результате лабораторного эксперимента наблюдалось в работе [5] (см. page 801, Fig. 7). В результате численного моделирования методом конечных элементов (МКЭ) в [6] показано притягивание продвигающейся трещины к границе раздела сред (см. Fig. 3, Fig. 7).

В [7] при описании процесса разрушения учитываются пределы упругости составляющих композит материалов, но не рассматривается их структура. Однако трещины часто оказываются межзеренными, и наличие периодической структуры существенно влияет на «раскрытие трещин, которое изменяется постепенно геометрически упорядоченным образом» ([1], стр. 96). В работе [8] показано, что критерии разрушения, принимающие во внимание характерный размер структуры материала, позволяют «расширить область применения по сравнению с традиционными критериями», хотя «вопрос о том, как этот размер связан с составом, структурой и, возможно, с другими параметрами реального материала, до сих пор не изучен». Поэтому проблемы построения простых, пригодных для инженерных расчетов аналитических моделей процесса разрушения композитов требуют разрешения [9–14]. Весьма актуальной является и задача продвижения трещины в сварном шве. В работе [14] обосновывается актуальность создания феноменологических моделей для прогнозирования разрушения слоистых материалов.

Настоящая работа является естественным продолжением и обобщением работ [15–17] по исследованию распространения трещины в композите в рамках модифицированной модели Леонова–Панасюка–Дагдейла [18, 19]. При квазистатическом нагружении с помощью МКЭ последовательно описан процесс распространения пластических зон в окрестности вершины трещины. Показано, что формы построенных пластических зон в биметалле существенно отличаются от таковых в однородной среде. Проведен сравнительный анализ результатов аналитического и численного моделирования разрушения биматериала при плоской деформации, обусловивший корректировку аналитической модели. Учет характерного линейного размера материала позволил вывести простые, пригодные в инженерных приложениях соотношения для критической нагрузки и критической длины зоны предразрушения, а также построить диаграммы разрушения. Установлено, что скорректированная аналитическая модель предлагает приемлемое прогнозирование величины критической разрушающей нагрузки для любых длин трещин.

2.    Постановка задачи

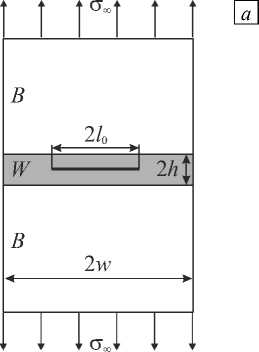
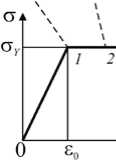
Рассмотрим биметаллическую пластину шириной 2 w , содержащую сварной шов в виде узкой полосы толщиной 2 h с центральной внутренней трещиной длиной 2 l ₀ (Рис. 1 а ). Буквами B и W обозначены основной металл и сварное соединение соответственно. На краях пластины заданы растягивающие напряжения σ_∞ , то есть реализуется первая мода разрушения. Оба материала биметаллической пластины являются идеальными упругопластическими с ( σ - ε )-диаграммой одноосного деформирования,

б

3     4

J------►

Ei      £

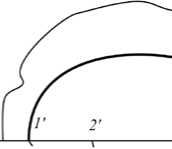
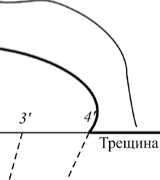
Рис. 1. Биметаллическая пластина со сварным швом (а); диаграмма деформирования (б) с точками 1–4 и соответствующими им точками 1’–4’ зоны предразрушения в окрестности левой вершины трещины показанной на рисунке 1б. Здесь: σY — предел текучести, ε0 — максимальная упругая деформация, ε1 — предельная деформация до разрушения. Введем параметр χ=(ε1-ε0)ε0, характеризующий соотношение предельной неупругой и максимальной упругой деформаций. Величину χ можно трактовать как относительную длину площадки текучести. Материал сварного шва обладает определенной структурой, имеет квазихрупкий или квазивязкий тип разрушения, причем характерный линейный размер r структурного элемента (например, диаметр зерна) предполагается известным.

3.    Модель разрушения материала

Предположим, что реальная острая внутренняя трещина–разрез нормального отрыва длиной 2 l ₀ распространяется прямолинейно в структурно-неоднородном материале. В модифицированной модели Леонова–Панасюка–Дагдейла [18, 19] помимо реальной трещины вводится в рассмотрение модельная трещина–разрез длиной 2 l = 2 l ₀ + 2 ∆ , где ∆ — длина зоны предразрушения или пластической зоны, расположенной на продолжении реальной трещины (Рис. 2 а ). В этой зоне возникают напряжения пластического деформирования, препятствующие раскрытию трещины и устраняющие сингулярность поля напряжений в окрестности её вершины. Предполагается, что напряжения здесь распределяются равномерно и равняются пределу текучести материала σ _Y . Полная постановка задачи распределения напряжений и смещений трещины нормального отрыва для упругопластических материалов рассматривается в нелинейной механике разрушения. Такую нелинейную задачу можно существенно упростить, используя классические представления линейной механики разрушения, когда трещина нормального отрыва моделируется как двусторонний разрез, а нелинейность задачи возникает только при описании зоны предразрушения. После введения модельной (дополнительной) трещины–разреза задача может рассматриваться не как упругопластическая, а как упругая. Напомним, что согласно классической модели Леонова–Панасюка–Дагдейла [20–22] пластический материал в зоне предразрушения, имеющей нулевой поперечник, стягивает берега трещины.

Зона предразрушения аппроксимируется прямоугольником со сторонами ∆ и a (Рис. 2 б ), причем длина зоны предразрушения ∆ определяется в процессе решения задачи разрушения, а поперечник a этой зоны целесообразно отождествить с поперечником зоны пластичности. В соответствии с предлагаемой модификацией модели Леонова–Панасюка–Дагдейла вершины реальной и модельной трещин следует различать. На рисунке 1 б приведена схема, качественно поясняющая взаимосвязь между точками 1 , 2 , 3 , 4 на ( σ - ε )-диаграмме и точками 1’ , 2’ , 3’ , 4’ в зоне предразрушения, расположенными на продолжении реальной трещины влево. Вне зоны предразрушения материал деформируется упруго, а на ее границе поведение меняется на неупругое, при этом точки зоны предразрушения находятся в области неупругого деформирования материала. В модели Леонова–Панасюка–Дагдейла предполагается, что на продолжении модельной трещины реализуется одноосное растяжение [23], поскольку к берегам трещины–разреза приложены постоянные напряжения σ _Y , которые притягивают берега друг к другу и, следовательно, действуют на материал растягивающим образом. В докритическом состоянии материал в вершине реальной трещины претерпевает удлинение ε<ε ₁ , которое в критическом состоянии совпадает с критическим удлинением ε=ε ₁ (см. в точке 4 на Рис. 1 б ). Пластическая зона в окрестности вершины трещины приближенно показана на рисунке 1 б для случая плоского напряженного состояния, а в виде двух лепестков на рисунке 2 б — для плоской деформации. Точка K является точкой пересечения прямой, параллельной оси O y и проходящей через вершину реальной трещины, с границей пластической зоны. Как будет показано далее, реальная форма пластической зоны весьма далека от идеализированных представлений [11, 23, 24].

а

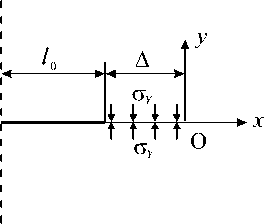
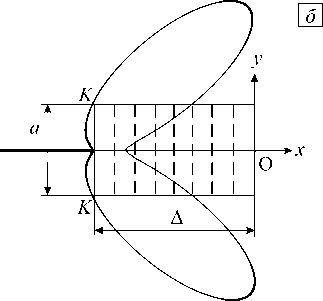
Рис. 2. Сжимающие напряжения, действующие в модели Леонова–Панасюка–Дагдейла на продолжении трещины ( а ); аппроксимация пластической зоны прямоугольной зоной предразрушения ( б )

При построении модели разрушения сварного соединения в условиях нормального отрыва воспользуемся интегральным критерием разрушения Нейбера–Новожилова [18, 19]:

1 ^r

— lay (x ,0) dx = a Y,   x > 0, r0

2v ( -A ) =5 * .

Здесь: a y ( x ,0) — нормальные напряжения на продолжении трещины; a Y — предел текучести при одноосном растяжении; г — характерный линейный размер структуры материала; 2 v = 2 v ( x ) — раскрытие трещины; 5 * — критическое раскрытие модельной трещины (при величине раскрытия, равной критическому значению, разрушается структура материала в вершине реальной трещины — граничной точке зоны предразрушения, то есть в точке 4 ' на рисунке 1 б ). Длина зоны предразрушения, если учесть длину интервала осреднения r , составляет только часть длины зоны пластичности. Силовой критерий (1), по терминологии Новожилова, является необходимым: процесс разрушения материала начинается тогда, когда осредненные по интервалу г нормальные напряжения достигают предела текучести a Y . При выполнении деформационного критерия (2) происходит катастрофическое разрушение образца. По этой причине совокупность условий (1), (2) называют достаточным критерием разрушения [18, 19].

Ограничимся случаем, когда упругие характеристики материалов биметаллической пластины совпадают, а прочностные различаются: a YW < a YB , где a YW — предел текучести материала сварного шва, a YB — предел текучести основного металла. Для применения интегрального критерия (1), (2) к обработке результатов численных или лабораторных экспериментов с образцами конечных размеров воспользуемся аналитическим выражением нормального напряжения a y ( x ,0) на продолжении трещины [17]:

a y ( x ,0) = -YK= + Y a , x >  0,                               ⁽3)

2nx где a„ — напряжения, заданные на краях пластины; KI = KIm + KIA — суммарный коэффициент интенсивности напряжений (КИН) в обобщенной модели Леонова-Панасюка-Дагдейла (KI„ > 0 — КИН, порождаемый напряжениями a„, KIA < 0 — КИН, порождаемый напряжениями aY, действующими в окрестности вершины модельной трещины в зоне предразрушения); Ys = Ys (l), Yr = Yr(l) — поправочные коэффициенты, учитывающие конечные размеры пластины. Для центральной внутренней трещины справочник [25, см. стр. 171] предлагает аппроксимирующую формулу Ys = ^/sec(nl)/(2w) (напомним, что w — полуширина пластины); коэффициент Yr = Yr(l) найдем из условия равновесия напряжений, приложенных к краям пластины, и напряжений, действующих на продолжении трещины: Yr =——--Y w!w . в случае бесконечной области коэффициенты Ys = Y,(l), Yr = Yr(l) тождественно

• 1    - l/w    ^1 - l/w

равны единице. После интегрирования по интервалу осреднения r уравнение (1) принимает вид:

YsKi = (aY - Yra„)H.(4)

Для раскрытия модельной трещины 2 v = 2 v ( x ), -A <  x <  0 используем в (2) представление [24]

2v(x) = — K В + O(|x|), Ki = Ki„+ Kia> 0, x < 0,(5)

p в котором учтем лишь первый член разложения. Здесь: к = 3 - 4v — для плоской деформации и к = (3 - v)/(1 + v) — для плоского напряженного состояния; v — коэффициент Пуассона; ц = E (2 (1 + v)) = a Y/(2e0 (1 + v))   — модуль сдвига материала, так как для идеального упругопластического материала E = aY /б0 , где E — модуль Юнга, е0 — максимальное упругое относительное удлинение. Уравнение (2) с помощью представления (5) запишем в виде

— Ys K i

Ц

учитывающем конечные размеры пластины.

В равенствах (4) и (6) K I . — КИН, обусловленный напряжениями ст . , вычисляется по формуле [25, стр. 171]: K_I „=ст.^[п 1 , а для КИН K _{1 Д} , порождаемого постоянными напряжениями ст Y , действующими согласно модели Леонова–Панасюка–Дагдейла в зоне предразрушения, выберем из справочника [25, стр. 41] выражение

1 Д

ст Y vn?

1--arcsin I 1-- п I 1

Отождествим поперечник зоны предразрушения с поперечником зоны пластичности при плоском напряженном состоянии в вершине реальной трещины [24]:

5 [ a = —I

4 п1

2 Y s K i . ) CT Y j .

Параметр максимального неупругого относительного удлинения е 1 - е ₀ определяется на основе ( ст - е )-диаграммы деформирования материала (см. Рис. 1 б) . Тогда критическую величину раскрытия трещины 5 * , при которой разрушается ближайший к вершине реальной трещины структурный элемент в зоне предразрушения, вычислим по формуле:

5 * = m ( е , -е ₀ ) а ,                                                 (8)

где m — поправочный коэффициент. Конечно, границы реальных пластических зон в окрестности вершины трещины лишь приближенно похожи на конфигурации, изображенные в [11, 23, 24]. При плоском напряженном состоянии с увеличением нагрузки узкая область пластических деформаций распространяется прямолинейно от вершины трещины по ее оси, принимая форму, похожую на узкий вытянутый прямоугольник. Такую форму пластической зоны, особенно при поперечном сдвиге, и преимущественное направление распространения трещины вдоль ее оси можно наблюдать как в численных, так и лабораторных экспериментах. В связи с этим в работе [17] для уточнения формулы поперечника зоны предразрушения обосновывается введение в соотношение (8) поправочного коэффициента m . Для определения величины этого коэффициента необходимо использовать непосредственно данные численного либо лабораторного экспериментов.

Теперь систему уравнений (4), (6), равносильную исходной системе уравнений (1), (2) при указанном выборе выражений для нормального напряжения ст y ( x ,0), раскрытия трещины 2v = 2 v ( x ) и КИН K I = K I . + K _{1 Д} , можно записать в виде

Y Vn 1U-

1 —arcsin

п

,

YVn 1U-

1--arcsin I 1 - n I

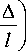
Д- h X ² = 0,

где X = ct./ct _y —безразмерная критическая нагрузка, в = ^/л г /2 , h = V2n% m1cY s2 /32. Здесь с = 5 для плоского напряженного состояния и с = (5 - 8 v + 8 v ²)/(1 -v ²) для плоской деформации, потому что для поперечника а зоны пластичности можно принять a = 5 1 X ² Y_s ²/8 в условиях плоского напряженного состояния и а = 1 X ² Y_s ²(5 - 8 v + 8 v ²)/8 —в условиях плоской деформации [17].

Расчеты показывают, что для любого значения коэффициента Пуассона 0 0,5 для плоской деформации выполняется неравенство 3,6 <  с <  5, причем с = 3,6 при v= 0,34. Исключая из системы уравнений (9), (10) член, заключенный в фигурные скобки, найдем точное выражение для критической длины зоны предразрушения:

h X ² в (1 - Y X ).

Прибегнув к приближению arcsin ( 1 - А/ 1 ) « л/ 2 - ^ 2 А/ 1 , погрешность которого при 0 <А/ 1 <  0,43

не превышает 6%, запишем систему уравнений (9), (10) в виде:

S

= 0,

А- h X ² = 0.

Заменив ТА в (12) согласно (11), получим квадратное уравнение относительно X , из которого определим приближенное значение критической разрушающей нагрузки: X ± = 2в/ ( 2 в Y r + f ± ^f ² - 4 gh ) , где f = Y s ТП / , g = 2Y s _V2A .

Возвращаясь к исходным переменным, видоизменим формулу критической нагрузки:

X ±

Y + Y . jH f l ± 1 1 JXmY. 1 ^r 2 4 r ( 4     2 n J

Величина X₊ , когда перед корнем выбирается знак « + », соответствует квазихрупкому (А/ 1 « 1), X- — квазивязкому ( А/ 1 ® 1) типу разрушения [17]. Формула (14), в рамках предлагаемой модели, имеет смысл, если х <  2л/( mcY s ).

Из приближенного уравнения (12) получим выражение

ТА

^

X( f + в Yr)-в g

а из (13) — два значения

2 h X

f ± V f2 - 4 gh

причем квазихрупкому типу разрушения соответствует ТА ₊ (в (16) перед корнем выбирается знак « - »), а квазивязкому типу разрушения — ТА - . Интересно, что при любом из приближенных значений (15) или (16) из системы уравнений (12), (13) следует точно такое же выражение для критической разрушающей нагрузки, какое дается формулой (14). А исключая из системы (12), (13) множитель после Y s , придем для критической длины А зоны предразрушения к такой же записи, как (11), которая получена из точной системы (9), (10).

Напомним, что уравнения (9), (12) так же, как исходное уравнение (1), выполняются для любых нагрузок X вблизи граничных точек зоны пластичности (см. точку 1 ' на рисунке 1 б) . Поэтому для любых нагрузок X , при которых возникает зона пластичности в окрестности вершины трещины, справедливо и представление (15), которое следует из (12). Однако уравнения (10) и (13) так же, как и уравнение (2), выполняются только при критических разрушающих нагрузках. Кроме того, приближенные выражения (6) и (8) для раскрытия трещины 2v ( -А ) и критического раскрытия 5 * вносят дополнительную погрешность в уравнения (10), (13), которые используются при выводе формул (11) и (16). Таким образом, имеем представление (14) для критической разрушающей нагрузки и три разные формулировки связи критической длины зоны предразрушения ТА с критической нагрузкой X — (11), (15), (16). Результаты численного моделирования, как будет показано далее, подтверждают применимость выражения (15) во всем диапазоне значений нагрузок.

При X ^ 0 в соотношениях (14)-(16) возможен предельный переход, который позволяет рассмотреть разрушение хрупких материалов (в таких материалах зона предразрушения отсутствует: А = 0). Согласно необходимому критерию разрушения (1) в случае хрупкого разрушения критические напряжения вычисляются по формуле

X = f Y+ Ys Д1I V r )

Аналитическое представление критической нагрузки (17) зависит только от одного параметра — характерного линейного размера элемента структуры r . В (14) же критическая нагрузка, полученная на основе достаточного критерия разрушения (1), (2), зависит от характерного линейного размера элемента структуры r, а также от величины %, характеризующей свойства материала в зоне предразрушения при пластическом деформировании.

Рассмотрим процесс деформирования при постепенном нагружении (0 < X <  1). Если необходимый критерий (1) не выполняется, то нелинейные эффекты не проявляются, исходная длина трещины 2 l ₀ остается неизменной. В случае, когда в достаточном критерии (1), (2) выполняется только условие (1), имеет место докритическое состояние системы, при котором наблюдается устойчивое увеличение длины модельной трещины: 2 1 = 2 1 ₀ + 2 А . Уравнение (1) в достаточном критерии (1), (2) определяет движение вершины модельной трещины. Если оба условия, и (1), и (2), реализуются, то система переходит в критическое состояние. Ближайшая к вершине трещины структура разрушается, поскольку длина зоны предразрушения достигает критического значения (15). При X = X ± неустойчивость критического состояния нелинейной системы очевидна. Соотношение (2) определяют обрыв силовых связей в ближайшей к вершине реальной трещины структуре зоны предразрушения. Таким образом, значения критических нагрузок, вычисленные по необходимому (см. (17)) и достаточному (см. (14)) критериям

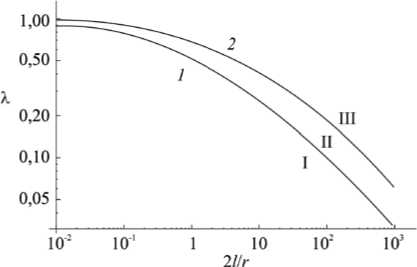
Рис. 3. Диаграммы квазихрупкого разрушения, полученные по необходимому (кривая 1 ) и достаточному (кривая 2 ) критериям

разрушения, являются нижней и верхней оценками критических нагрузок рассматриваемой нелинейной системы.

На рисунке 3 в двойных логарифмических координатах приведены диаграммы квазихрупкого разрушения, полученные по необходимому (17) (кривая 1 ) и достаточному (14) (кривая 2 ) критериям. Плоскость (2 1/r , X ) разбивается кривыми 1 , 2 на три области. В области I длина исходной трещины не меняется (трещина устойчива), в области II она увеличивается на величину, равную длине зоны предразрушения (трещина подрастает, оставаясь устойчивой), в области III имеет место катастрофический рост (трещина неустойчива).

4.    Компьютерное моделирование

Для численного моделирования реальной формы пластической зоны в окрестности вершины центральной трещины, расположенной внутри сварного соединения, использовался МКЭ. Рассматривалась биметаллическая квадратная пластина единичной толщины, растягиваемая напряжениями ст , , приложенными на ее кромке, при наличии центральной внутренней трещины и условиях плоского деформированного состояния (Рис. 1 а ). Геометрические размеры пластины были такими: ширина 2 w = 100 мм; толщина сварного шва 2 h = 2 мм; длина трещины 2 1 варьировалась от 12 до 48 мм. При конечно-элементном анализе, в силу наличия двух плоскостей симметрии, в расчет принималась лишь 1/4 пластины. Оба материала пластины считались идеальными упругопластическими со следующими характеристиками: модули Юнга Е_В = E W = 200 ГПа, коэффициенты Пуассона v _В = v _W = 0,25, пределы текучести ст YB = 800 МПа, ст YW = 400 МПа (нижние индексы В и W означают основной металл и сварной шов соответственно).

Расчетная область покрывалась неравномерной сеткой из 612500 4-угольных элементов с линейной аппроксимацией перемещений. В сварном шве производилось сгущение сетки до размера 0,02 мм. Отношение размера элемента в окрестности вершины трещины к ее длине в самом неблагоприятном случае ( 1 = 6) составляло 1/300, что соответствовало рекомендациям, приведенным в [26]. Традиционное сгущение сетки к вершине трещины, применяемое в подобных задачах, не производилось, поскольку целью численного исследования являлось не вычисление как можно более точных значений напряжений и деформаций в окрестности вершины, а наиболее точное определение формы и размеров пластической зоны. В процессе нагружения внешняя нагрузка ст „ монотонно возрастала по линейному закону от нуля до ст YW . При уровнях нагружения X = ст„/ст YW >  0,2 в окрестности вершины трещины возникали большие пластические деформации, поэтому задача решалась в текущей лагранжевой постановке с учетом физической и геометрической нелинейностей на основе общих уравнений механики деформируемого твердого тела [27] с использованием в качестве меры напряжений тензора напряжений Коши, а в качестве меры деформаций — тензора логарифмических деформаций Генки.

Рассмотрим определяющие соотношения теории пластического течения, справедливые при больших деформациях. Пусть v = u — вектор скорости материальных частиц деформируемого тела, u — вектор перемещения, d — симметричный тензор скорости деформаций, s — симметричный тензор напряжений Коши. Кинематические соотношения (связь тензора скорости деформаций с тензором градиента скорости) имеют вид d = 1(Vv + VvT), где VvT — тензор градиента скорости; V — пространственный набла- вектор. Основная гипотеза теории пластического течения, позволяющая учесть в определяющих соотношениях одновременно упругую и пластическую составляющие деформаций, состоит в аддитивном представлении тензора скорости деформаций: d = de + dp, где de и dp — упругая и пластическая составляющие тензора скорости деформаций, которые следуют из законов упругого и пластического деформирования. Для изотропных материалов эти составляющие находятся из закона Гука (упругая составляющая тензора скорости деформаций) и ассоциированного закона пластичности:

s ^H = C E : d e = C E :( d - d p ),      d p = c X — .

d s

Здесь: s ^H — объективная производная Хилла тензора напряжений Коши s : s ^H = s - w ■ s + s ■ w + s tr d , где w = ( V v T -V v ) /2 — кососимметричный тензор вихря, tr — след тензора второго ранга; C E — тензор четвертого ранга для изотропной упругой среды со следующими компонентами в декартовой системе координат:

^E ijkl

E

1 + v

1,„                  V