Моделирование процесса течения газа в канале, содержащем лед, сопровождаемого его тепловым разрушением

В последние несколько лет зафиксировано образование кратеров совершенно правильной осесимметричной геометрической формы в зонах вечной мерзлоты, где расположены богатейшие углеводородные залежи. Одной из таких территорий является Ямальский полуостров, на котором идет промышленная добыча газа и нефти. Анализ возникновения таких явлений требует комплексного подхода. С одной стороны, необходимо учитывать текущее состояние геологической структуры зоны вечной мерзлоты. Так, в работе [1] показано, что в настоящее время за счет потепления климата наблюдается обширное таяние, что приводит к деградации зоны вечной мерзлоты как по площади, так и по охвату толщи земли. С другой стороны, необходимо учитывать механизмы образования таких кратеров. В силу того, что интерес к подобным аномалиям появился совсем недавно, имеется небольшое количество работ, посвященных их изучению. В работе [2] анализируется процесс роста ямальской воронки по мониторинговым снимкам земной поверхности из космоса и результатам проведенной экспедиции. Следует отметить, что формирование ямальского кратера длилось продолжительное время и сопровождалось выбросом породы, что напоминало вылет пробки из бутылки с шампанским. На сегодняшний день известно более чем о пяти таких кратерах. Поэтому установление и моделирование причин, вызывающих их образование, является весьма актуальным для безопасной эксплуатации жилых и промышленных объектов в области вечной мерзлоты, особенно вблизи месторождений полезных ископаемых.

Исходя из множества различных гипотез и оценок причин возникновения этих геологических аномалий можно выделить два основных фактора. Первый — локальное ослабление прочностных характеристик приповерхностного слоя земной коры, состоящего в основном из льда. Второй — наличие ловушек (объемов пород, способных вмещать, аккумулировать и консервировать нефть и/или газ), образующихся вследствие геологических и термобарических изменений. По-видимому, названные факторы можно объяснить проникновением теплого газа из более глубоких слоев в приповерхностной слой. Можно также предположить, что кратеры (или воронки) зарождаются спонтанно (лавинообразно).

Согласно имеющимся данным очагами кратеров являются места (оси) тектонических разломов [3–5]. Начальный этап роста щелей за счет термического разрушения ледяной стенки (или мерзлых пород, где лед является «цементирующим» элементом), протекает медленно. По мере расширения щели (скважины) происходит увеличение скорости потока газа, что может приводить к интенсификации процесса выброса продуктов разрушения, который будет продолжаться до момента снижения давления в полости под ледяной (мерзлой) породой до атмосферного.

В данной работе представлен начальный этап течения газа в вертикальном канале конечной длины, окруженном льдом и инертной средой, не подвергающейся фазовым переходам (это глина, песок и другие твердые породы), то есть за время пребывания продуктов истечения в канале изменение его радиуса будет незначительным.

Заметим, что при описании течения потоков газа в каналах следует помнить, что важную роль играют процессы теплопередачи. Знание параметров последних необходимо при проектировании промышленных объектов. В работе [6] моделируется теплоотдача от газожидкостной смеси, текущей в скважине, в мерзлую породу с учетом происходящих в породе фазовых переходов. Здесь также анализируется влияние твердых отложений на внутренних стенках подъемной колонны скважины. Течению газожидкостного потока в каналах, находящихся в газогидратных массивах, посвящена работа [7]. Для теоретического описания течения двухфазного потока получена система дифференциальных уравнений, связывающих скорости потока, давление и температуру, совместно с которой решается задача определения интенсивности вымывания газогидрата с учетом тепловых полей вокруг скважины. Численная реализация проведена в два этапа. На первом этапе решается задача Коши для установления основных параметров потока, а на втором этапе находятся радиусы канала и оценивается тепловое влияние скважины.

Целью представленной работы является теоретическое описание в стационарном приближении процесса течения газожидкостного потока в вертикальном канале, в основном состоящем из льда. Течение сопровождается разрушением стенок канала.

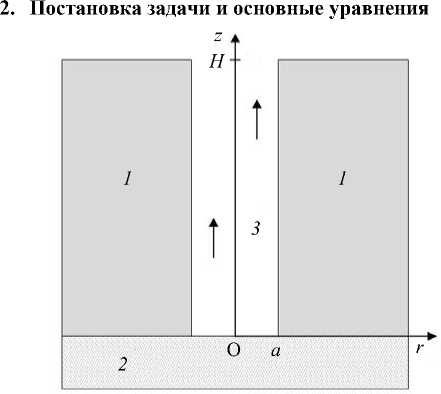
Рис. 1. Технологическая схема: 1 – мерзлая порода (лед, глина, песок и другое, 2 – пласт залежи газа, 3 – газожидкостной поток

Пусть имеется вертикальный цилиндрический канал в мерзлой породе 1 , состоящей в основном из льда, глины, песка и другого, через которую из пласта залежи 2 к поверхности земли движется газ. Ось z направим вертикально вверх — по направлению движения газа. Положим, что процесс движения газа сопровождается разрушением стенок канала. Продуктами разрушения, поступающими в поток, будем считать растаявший лед (воду) и породу (инертную среду). В результате поток 3 в вертикальном канале состоит из газа, воды и породы, то есть является трехфазным (Рис. 1). Объемное содержание отдельной фазы обозначим как a i , где индексы i = g, w, s относятся, соответственно, к газу, воде и инертной среде, причем a _g + a w + a s = 1.

Уравнения сохранения массы для компонентов потока запишем в односкоростном приближении с учетом того, что массовый расход потока в канале будет изменяться за счет поступления продуктов

разрушения канала — воды и породы:

dM = J w + J s , dz dM w = J w ,                                        (1) dz dMs- = J s . dz

Здесь M = р S и , M w = р w a _wS и , M s = р s а _sS и — массовые расходы потока и продуктов разложения стенок канала. Массовый расход газа определяется как

M g = р g a g S и .

В формулах (1), (2) обозначено: и — скорость потока; р — общая плотность потока, связанная с плотностями компонентов р = р g a g + р w a w + р _s а _s ; S = п a ² — площадь сечения канала, где a — его радиус; J k ( k = w , s ) — интенсивности поступления воды и инертной среды, образовавшейся за счет абляции:

Jk = 2п a л! 1 + a '2jk, где jk — отнесенные, соответственно, к единице длины канала и к единице площади стенки интенсивности поступления воды и инертной среды; a' = дa/дz . Для интенсивности поступления влаги и инертной фазы в поток на основе закона сохранения массы можем записать: jw = р I a Ia , js = р s (1 - a I) a. Здесь: a I — коэффициент объемного содержания льда в породе; a = дa/дt.

Уравнение импульсов для всей трехфазной системы представим в виде [8]:

d- ⁽ M^"Sp ^- S р g ^- F ,                          (3)

dz         дz где p — давление в потоке, g — ускорение силы тяжести, F = 2пaт — сила гидравлического трения, отнесенная к единице высоты канала, для определения которой используем выражение:

т = ^ри ² /8 .

Здесь для определения коэффициента гидравлического сопротивления взята формула из [9]

§ = (1,82lg (Re)-1,64)-2, применимая для широкого диапазона чисел Рейнольдса: 2300 < Re < 106, где критерий Рейнольдса находится как

Re = 2aри/цg , цg — коэффициент динамической вязкости газа.

Запишем также уравнение для изменения энергии потока:

( f d- M I e + dz V

и ²

= - v( SP ° ) - S р g u + J w^ e w- + J s e s - Q •                       (4)

V

Здесь: Q = 2 п a V1 + a '2 q — интенсивность отвода тепла, отнесенная к единице длины канала, где q — интенсивность теплообмена между трехфазным потоком и стенкой канала, отнесенная к единице площади стенки канала; e = e_g + e_w + e s , где e_g = c_g ( w T , e_w = c w T , e_s = C s T , при этом c_g ( w ) , c_w , C s — удельные теплоемкости компонентов потока (для газа — при постоянном объеме). В дальнейшем во всех вышеприведенных уравнениях будем пренебрегать изменением a '2 по сравнению с единицей.

Газ считаем калорически совершенным p =pgRgT ,

а воду и инертную фазу — несжимаемыми; p w , p s = const.

3. Описание абляции стенок

Будем полагать, что поток тепла со стороны трехфазного потока к стенке тратится на расплавление льда вблизи стенки и нагрев мерзлой породы, причем градиент температуры вдоль скважины мал по сравнению с радиальным градиентом:

d t a t — « — a z a r

Тогда условие баланса тепла на поверхности стенки канала можем записать как

X_G — + q = p,a, l_Ec i .

° a r            I ^{1 11}

Здесь: X _G = X , a , + X _s ( 1 -a , ) — коэффициент теплопроводности мерзлого грунта, состоящего из льда и породы соответственно; l _I — теплота плавления льда. Нижние индексы G , I , s соответствуют мерзлой породе, льду и инертной породе соответственно.

Для интенсивности теплового потока воспользуемся формулой

q =₽ ( T - T s ) ) ,

где P = X g Nu/(2 a ) — коэффициент конвективного теплообмена, T _{( s}) — температура на стенке канала, равная температуре плавления льда, Nu — число Нуссельта, связанное с числом Прандтля Pr = ц g c g ( w )/ X _g соотношением [9, 10]:

Nu = (V 8 ) RePr/ ( 1 + 12,7 71/ 8 ( Pr^2/3 - 1 ) ) .

Для определения температурных полей вокруг канала запишем уравнение теплопроводности

a t  , 1 a ( a t pGcG — = XG--1 r—° dt       r ar I   ar

.

Здесь p _G c _G = p ,c, a , + p s c s ( 1 - a , ) — объемная теплоемкость мерзлой породы.

Следует отметить, что температурные поля вокруг канала в общем случае являются нестационарными, однако в течение характерных времен процессов, имеющих место в скважине, влияние их нестационарности несущественно [11]. Поэтому для определения радиальных температурных полей вокруг канала воспользуемся решением уравнения теплопроводности по аналогии с методом последовательной смены стационарных состояний [12]. Согласно этому методу, производную по времени в первом приближении можно отбросить ( d T / 81 = 0 ) , в результате чего для температуры получается уравнение, описывающее ее стационарное распределение. В этом случае уравнение (8) можно представить в виде

^^ ^Cd T G L_o r                              .

r a r i    a r i

Его можно решить непосредственным интегрированием.

Для задания граничных условий введем понятие радиуса теплового влияния скважины a ₀ . Тогда на границе контакта скважины с окружающей мерзлой породой ( r = а ) будем считать, что температура равна температуре плавления льда: T _G = T₍ s ) , а при r = а + а ₀ — начальной температуре: T_G = T ₀ . Для начального момента времени поле температуры удовлетворяет условию T_G = T ₀ ( а <  r <  а + а ₀) . Тогда из уравнения (9) с учетом принятых граничных условий получим следующее выражение:

т

TG

= т

T o

+

т -Т

T ( s ) T 0

ln ( a, ( a + a 0 ))

ln ( r / ( a +

a 0 )) .

Подставляя решение (10) в условие баланса тепла (6), придем к выражению закона скорости роста радиуса канала a следующего вида:

da =    ¹     X g    ^T( s ) - T o    + q

dt   p I a III I a In ( a /( a + a ₀) )

4. Определение радиуса теплового влияния скважины

Чтобы вывести закон изменения радиуса теплового влияния a0 со временем, воспользуемся решением уравнения (8) в плоской постановке d T , d2 T pr cr—G = xr —G G G at     G ax2

с граничными условиями T _G = T s ) (при x = 0), T g = T o при x = a 0 . Его квазистационарное решение ( д T /д t = 0) имеет вид:

T

TG

= T > +

т,

T ( s )

-

т

T ₀

x .

a ₀

Запишем условие баланса тепла:

д a L „ ™1 Р T g )

- J ^p G c G^T d     ^X g I      I .

^a t J              I a x л

Подставив (13) в (14) и проинтегрировав, получим выражение для определения длины участка, на котором происходит изменение теплового поля:

a

0 =

1 ² ( T s ) - T ) T ) + T

к t x .

Здесь К = X _G /( p _G c _G ) — коэффициент температуропроводности мерзлой породы.

• 5.    Уравнения для численных расчетов

Для численного моделирования движения потока вдоль канала методом Рунге–Кутты [13] в качестве неизвестных примем следующие из введенных выше параметров (или функций): M , M_w , M_s , M_g , p , T и и . Уравнения сохранения массы (1) разрешим относительно производных M , M w и M s по координате z , где параметр M g находится из формулы (2). Уравнение импульсов (3) умножим на и , найденное выражение вычтем из уравнения энергии (4) и, проведя некоторые математические преобразования, придем к уравнению для температуры:

mcdT = - Sp 1^- cT ( J w + J s ) + J w ^ w + J_se_s + F u- Q .                    (16)

dz        a z

Для отыскания функции u воспользуемся уравнением Менделеева-Клапейрона (5) с учетом массового расхода вещества в канале и предположения, что газовая фаза является преобладающей: p ® pg . Тогда p = mRgT/(uS).

Дифференцирование уравнения (17) по z дает уравнение:

dp R„mdT R„mT d u RJ ( _т m dS ) g =       1 J + J I .

dz   u S dz   u ² S dz   u S |          S dz J

Разрешая (18) относительно dp/dz , dT/dz , d и/ dz на основе уравнений (3), (16) и (18), получим:

dp _ А ⁽ p )       dT _ А ^{( T} )        d u _ A ^{( u )}

dz A dz A dz A

A ^{( p} )

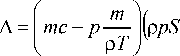
₂\  ₂ mm

+ m ) + p p m-- p T P P

1I              m

= pP\ mc - p — ll      PT

( Sf ^{( p} ) + mf ^{( u )} )

⁺ m p T ( f * T ) ⁺ pf )

A ⁽ T ) = ( p pS² + m ² )( f ⁽ T ) + pf ^(u) ) - p ²pp mp ( Sf ^{( p} ) + mf ^(u) ) ,

A ^{( u )} = 21 m a ⁽ p ) - -m - A ^{( T} ) - f ^{( u )} A I s Ip p      p t           ^{J ,}

f ^{( p} ) =- S p g - F - ( J w + J s ) - pdS,

f ^{( T} ) = - cT ( J w + J s ) + J w e w + J s e s + F u- Q ,

.(u)_ J    ■!   ddS f =1u.

p   p dz

Итак, численное решение задачи течения восходящего потока в вертикальной скважине состоит из двух этапов. На первом этапе решается задача Коши для уравнений (1) и (19) при заданных на входе ( z = 0) начальных значениях давления p ₀ , температуры T ₀ и скорости u ₀ при «замороженных» по времени распределениях а и а ₀ , причем начальные значения подбираются таким образом, чтобы давление на выходе из скважины ( z = H ) было больше или равно атмосферному ( p e >  p _атм ) и скорость не превышала скорости звука ( u < u e ) при текущем значении давления, где u e = 7у p e /p e , у — показатель адиабаты газа. Следует отметить, что данное предположение основано на известной теории истечения газа [14]. На втором этапе с использованием найденных распределений параметров потока совершается шаг по времени и решается задача определения радиусов а и а ₀ с помощью формул (11) и (15) соответственно.

• 6.    Результаты численных расчетов

  На основе полученной системы дифференциальных уравнений проведены численные расчеты при следующих значениях теплофизических параметров системы: X _s = 0,7 Вт/(м ■ K); X I = 2,2 Вт/(м ■ K); X _g = 0,032Вт/(м ■ K); 1, = 3 ■Ю ⁵ Дж/кг; p , = 917кг/м³; p s = 2300кг/м³; p w = 1000кг/м³; с , = 2100 Дж/ ( кг ■ К ) ; c_s = 880 Дж/ ( кг ■ К ) ; c_g ( w ) = 1680 Дж /( кг ■ К ) ; g = 9,81 м/с²; ц _g = 1,1 - 10 - ⁵ Па ■ с ; R_g = 520 Дж /( кг ■ К ) ; T • s ) = 273 К ; T_g = 293 K ; T ₀ = 273K; P_g = 0,5МПа ; а , = 0,86; a = 0,01м ; H = 40 м .

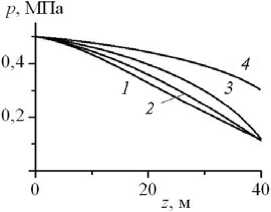
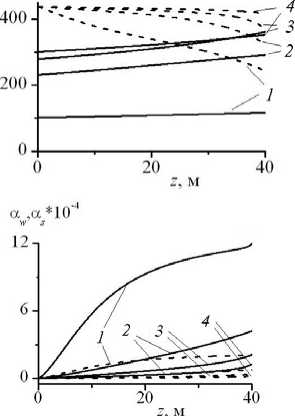
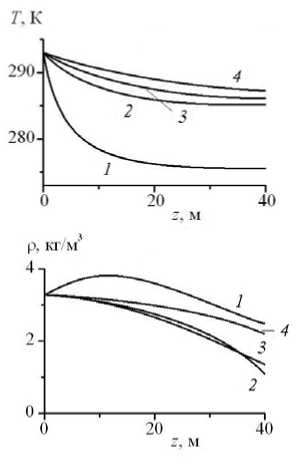
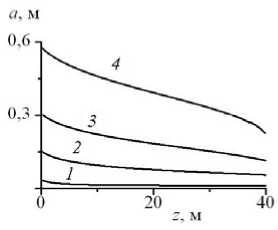
На рисунке 2 представлены распределения давления, температуры , скорости , общей плотности потока, объемного содержания компонентов (воды и породы) в потоке , радиуса канала по высоте z в различные моменты времени 6, 30, 60 и 90 мин соответственно. На начальном участке течение (при малых значениях радиуса скважины a <  0,3 м) характеризуется дозвуковым режимом (скорость потока на выходе не достигает скорости звука), давление на выходе остается постоянным и приблизительно равным атмосферному, температура потока по высоте успевает понизиться на десятки градусов и имеет наименьшего значения на выходе. Со временем наблюдается повышение температуры вдоль всего канала. Из-за высокого перепада температур вблизи входа в скважину поступает большое количество продуктов разрушения стенок (вода и порода), поэтому плотность потока в первые 6 минут увеличивается. Разрушение канала при положительной температуре происходит по всей его длине, поэтому объемное содержание продуктов разрушения с высотой будет всегда расти, и его максимальные значения будут соответствовать начальному участку, где радиус канала небольшой, а с увеличением радиуса общая объемная доля продуктов разрушения будет снижаться.

Приблизительно через 60 мин после начала выхода газа (при a >  0,3 м) поведение параметров потока начинает меняться. Скорость потока на выходе из канала приближается к скорости звука (то есть имеет место эффект звукового запирания). При этом предельном режиме поток, выходящий из канала, может выплескиваться в направлении от центра скважины. Дальнейшее расширение скважины сопровождается увеличением давления на выходе, повышением интенсивности роста радиуса канала со временем (это связано с уменьшением удельной поверхности канала по отношению к массе потока).

V. м с

а

в

д

б

г

е

Рис. 2 . Распределение давления ( а ), температуры ( б ), скорости (штриховые линии отвечают скорости звука при текущем значении давления) ( в ), общей плотности ( г ), объемного содержания компонентов (сплошные линии соответствуют воде, штриховые породе) ( д ) и радиуса ( е ) по высоте z в различные моменты времени t , мин: 6 (кривая 1 ); 30 ( 2 ); 60 ( 3 ); 90( 4 )

Можно предположить, что на этом этапе процесс течения потока в канале приобретает лавинообразный характер, что может спровоцировать разрушение ледяной стенки и возникновение воронки.

Течение на последующих участках характеризуется снижением скорости потока (дозвуковой режим) и постепенным выравниванием профилей давления, температуры, скорости, плотности и объемного содержания продуктов разрушения.

• 7.    Заключение

В работе исследован процесс разрушения вертикального канала, в основном состоящего из льда, под действием протекающего в нем теплого газа. Получена система дифференциальных уравнений для нахождения распределений основных параметров газожидкостного потока по высоте канала (давления, температуры и скорости). Численная реализация проводилась методом Рунге–Кутты. Найдены критические значения радиуса по высоте, при которых меняется режим течения. Установлено, что при малых значениях радиуса режим течения газа является дозвуковым, и газовый поток на первой половине пути охлаждается до температуры, близкой к температуре породы. С увеличением радиуса тепловой поток из-за неполного охлаждения выносит часть тепла к поверхности. Определено критическое значение радиуса, при котором скорость выхода потока достигает скорости звука при данном значении давления. С дальнейшим увеличением радиуса скорость потока на выходе начинает снижаться и не достигает дозвукового режима.