Моделирование процесса вакуум-сублимационной сушки высокопористого материала в сверхвысокочастотном поле

Существенно интенсифицировать процесс вакуум-сублимационного обезвоживания позволяет использование энергии электрических токов сверхвысокой частоты (СВЧ). Характер СВЧ нагрева, как известно, способствует резкой интенсификации процессов тепло- и массообмена, так как прогрев материала происходит по всему объему, при этом градиенты температуры и влажности совпадают по направлению. Однако, если процесс обезвоживания развивается по принципу постепенного углубления зоны сублимации, то при рассматриваемом способе энергоподвода вполне возможен перегрев внутренних слоев сушимого материала.

Материалы и методы

Проанализировав описанный процесс сушки с точки зрения его моделирования, выделим ряд наиболее важных, на наш взгляд, аспектов.

• 1.    Зона парового затвора и вакуумированный объем камеры характеризуются принципиально разными условиями внешнего (по отношению к объекту сушки) тепло- и массообмена.

• 2.    Одной из главных особенностей процесса является наличие у объекта сушки развитой пористой структуры, многократно увеличивающей поверхность парообразования. В связи с этим обезвоживание материала не происходит по «классическому» принципу углубления зоны сублимации, а носит ярко выраженный объемный характер: зоной сублимации в данном случае является сразу весь объем материала, а поверхностью сублимации – вся его пористая структура.

• 3.    В процессах вспучивания (при «пористом замораживании») и обезвоживания материала изменяются его геометрические размеры и пористая структура. При моделировании следует учесть не только переменность соответствующих характеристик (ширина жгута, пористость и др.), но и установить закон их изменения.

• 4.    В процессе сушки материала содержащаяся в нем влага переходит из жидкой фазы в твердую (при испарительном замораживании) и, возможно, обратно (в случае перегрева замороженного материала в поле СВЧ). Находясь в прямой зависимости от парообразования и СВЧ нагрева, процессы кристаллизации и плавления в высокопористом материале также носят сложный объемный характер, что требует при моделировании разработки специального способа их описания.

• 5.    Главными особенностями СВЧ нагрева являются его объемный характер и селективность поглощения электромагнитной энергии различными составляющими влагосодержащих

• 6.    Сложный объемный характер процессов испарения и сублимации обуславливает необходимость анализа поля влагосодержания для всего объема материала. Кроме того, должна быть учтена неоднородность содержащейся в материале влаги. При температурах и давлениях, создаваемых в процессе сублимационной сушки, в материале содержится три вида (формы) влаги – свободная вымороженная, свободная невымороженная и связанная. При этом удаление влаги из материала происходит в указанной последовательности. Неоднородность влаги оказывает существенное влияние на все тепломассообменные процессы, происходящие в ходе сушки – СВЧ нагрев, парообразование, кристаллизацию-плавление и прочее.

• 7.    Рассматриваемый процесс сушки характеризуется интенсивным тепло- и массообменом. При вводе материала в сублимационную камеру, а также при СВЧ нагреве во всем объеме материала происходит бурное образование пара. Возникающее при этом избыточное давление не успевает мгновенно релаксироваться через пористую структуру материала, вследствие чего внутри последнего появляется значительный градиент давления, оказывающий, в свою очередь, существенное влияние на тепло-и массообменные процессы.

• 8.    В ходе анализируемого процесса внутри материала и вне его происходит стремительное изменение температуры, влажности и давления. Таким образом, теплофизические и термодинамические характеристики, зависящие от этих величин, не могут быть приняты постоянными.

• 9.    Для установившегося режима работы сушилки рассматриваемый процесс можно считать квазистационарным. Поступательный и равномерный характер перемещения материала вдоль сублимационной камеры позволяет сделать замену τ = z/v , где z – расстояние, пройденное материалом вдоль камеры; v – скорость перемещения материала. При этом все интересующие нас частные производные по времени изменяются по схеме ∂/∂ τ = v ∂ ∂ z .

• 10.    Принимая во внимание, что в ходе сушки имеют место процессы кристаллизации-плавления и СВЧ нагрева, а также объемный характер этих процессов, добавим в уравнение теплопроводности слагаемые Q кр и Q свч, обозначающие удельную мощность внутренних источников теплоты, связанных соответственно с кристаллизацией-плавлением и СВЧ нагревом.

• 11.    Учитывая стремительность изменения температуры материала в процессе сушки, добавим в уравнение фильтрационного переноса пары слагаемых, отражающий изменение давления внутри материала при перепаде температур.

• 12.    Приняв во внимание геометрическую форму объекта сушки, будем проводить рассмотрение в цилиндрической системе координат, совместив координатную ось с продольной осью жгута материала. Будем полагать, что анализируемый процесс обладает свойством полной осевой симметрии.

материалов (сухой скелет материала, жидкость, лед, пар и прочее). Естественно, что по мере изменения в процессе сушки размеров, структуры, температуры и влажности материала, а также агрегатного состояния содержащейся влаги, диэлектрические свойства материала могут существенно меняться.

Из выше сказанного следует, что для адекватного описания внутреннего тепло- и массообмена необходим анализ полей всех трех основных потенциалов переноса в капиллярнопористых телах – температуры, влагосодержания и давления.

Проведенный анализ показывает, что исследуемый процесс сушки может быть расчленен на различные «элементарные» процессы - перенос теплоты и массы, парообразование (испарение и сублимация), вспучивание с образованием пористой структуры, кристаллизация и плавление, СВЧ нагрев. Этим обстоятельством мы воспользовались как при разработке модели процесса, так и при ее изложении в данной работе, синтезировав общую модель из нескольких подмоделей, каждая из которых описывает тот или иной «элементарный» процесс.

Результаты

Общая формулировка модели тепло-и массообмена. С учетом сделанных замечаний опишем происходящие внутри материала тепло- и массообменные процессы следующей системой уравнений:

.  51   1 д (, д t)

cyv— =--1 Ar— I- дz  r дr v   дr)           (1)

• - ^Г с Jm^KS + й р + ^Q CB4 ;

д u   1 д [ v, = т1 am 2

дz   r д r V д u

д r

1 д

r д r

1 д

y r д r

а   д t

: m 2 ^2 r — д r jmKS

;

д p   1 д ( .    д p )

cpyv=1 Ap 1 rI + p  дz  r д r v  д r )

„  д t

+ nb_Tv --+ jK,.

T     mS

дz

при 0 < r < R, 0 < z < H, где r, z - цилиндрические координаты: r -внутренний радиус жгута, м; z - текущая длина жгута, отсчитываемая от точки выхода материала из экструдера, м; R - радиус жгута, м; H - общая длина жгута (высота сублимационной камеры), м; v - скорость движения материала, м/с; t - температура, К; и - удельное влагосодержание, кг влаги/кг сух. вещ.; p - давление водных паров в материале, Па; c - приведенная удельная теплоемкость материала, Дж/(кг сух. вещ.^К); у - плотность сухого скелета материала (объемная концентрация сухого вещества), кг сух. вещ./м3; 2 - коэффициент теплопроводности материала, Вт/(м-К); rс - скрытая теплота парообразования, Дж/кг; Qкр - удельная мощность внутреннего источника теплоты, связанного с процессами кристаллизации и плавления, Вт/м3;  Qсвч - удельная мощность внутреннего источника теплоты, связанного с СВЧ нагревом, Вт/м3; am2 - коэффициент диффузии жидкости, м2/с; 32 - от носительный коэффициент термодиффузии жидкости, кг влаги/(кг сух. вещ.-К); 2, 1, А,2 -коэффициенты молярного переноса пара и жидкости, кг влаги/(м^Па); jm - локальная интенсивность внутреннего парообразования, кг/(м2^с); Ks - степень развития внутренней поверхности парообразования, м2/м3;   с, - удельная массоемкость материала по отношению к влажному воздуху при его молярном переносе, кг влаги/(кг сух. вещ.^Па); П- пористость материала;  Ьт - коэффициент, характеризую щий интенсивность расширения пара в порах от нагревания, кг/(м3^К) (для идеального газа ПЬт = cАР /1).

В данной системе уравнение (1) описывает внутренний теплообмен, движущими силами которого в общем случае являются теплопроводность, парообразование, кристаллизация (или плавление) и СВЧ нагрев. Уравнение (2) описывает внутренний массообмен, происходящий за счет молярно-диффузионного переноса жидкости и парообразования. Уравнением (3) определяется изменение общего давления внутри материала при фильтрационном переносе пара, изменении температуры материала и увеличении количества пара за счет испарения или сублимации.

При составлении этих уравнений мы пренебрегли тепло- и влагопроводностью вдоль оси z, исходя из следующих соображений. Во-первых, передача тепла теплопроводностью и молярнодиффузионный перенос влаги вдоль жгута материала осуществляются гораздо медленнее, чем в поперечном направлении, в силу очевидной анизотропии жгута: поры, образующиеся в процессе испарительного замораживания струями вырывающегося на поверхность пара, располагаются преимущественно в поперечном направлении, что затрудняет продольный перенос тепла и массы. Во-вторых, скорость тепло- и влагопроводности значительно меньше скорости движения материала, т. е. передача состояния вдоль оси z определяется, главным образом, механическим перемещением материала.

Для однозначности решения системы дифференциальных уравнений (1)–(3) дополним ее граничными условиями t Iz=0=t0; u Iz=0=u0; p Iz=0=po; (4)

r = 0

r = 0

|    = 0; (5)

r = 0

+ ^{a (} t ¹ r = R

- t с ) ⁺ r c q_m 2 = 0;

Поскольку в условиях глубокого вакуума теплообмен конвекцией незначителен (коэффициент α близок к нулю), то данное слагаемое можно учитывать только для зоны парового затвора, опустив его при рассмотрении вакуумированного объема сублимационной камеры.

Совершенно ясно, что анализ переноса жидкости внутри материала имеет смысл проводить лишь для начального периода испарительного замораживания, в дальнейшем этим переносом по ряду причин можно пренебречь, что позволяет заметно упростить модель тепло- и массообмена. Действительно, если пренебречь миграцией жидкости внутри материала, то система (1)–(3) перепишется следующим образом:

. д t 1 д|, д 1 1

cvv— =--1 Ar— I — дz  r dr v   дr J           (9)

- r c J m ^KS ^{+ Q} kp ^{+ Q} CB4 ;

| 5 U 1            e I dt am2 Y I — I + am2^71“

\ ^d r J r = R           \^д r

v d u =- j m K S ;          (10)

oz      у

+ q m 2    ⁰;

^A p ¹ f I p 1    ^{+ a} P ⁽ P ¹ r = R - P c ) = ^{0,     (8)}

V r J r = R

dp   1 д f .   д p 1

cPYv— =--1 A, r— I + p   dz  r dr V p dr J dt

^{+ ПЬ}Т v r ⁺ j m ^KS д z

при 0 <  r <  R , z * <  z <  H ,

где t 0 , u 0 , p 0 – распределение температуры, влагосодержания и давления при выходе материала из экструдера (для простоты эти величины можно считать постоянными); t с , p с – температура и давление влажного воздуха среды у поверхности материала (эти величины переменны по z , имея, в частности, разные значения для зоны парового затвора и вакуумированного объема сублимационной камеры); α – коэффициент теплообмена, Вт/(м²∙К); α p – коэффициент массообмена при наличии избыточного давления в материале, кг/(м²∙с∙Па); q m 2 – интенсивность испарения жидкости на внешней поверхности материала, кг/(м²∙с).

Здесь условия (4) определяют начальное распределение температуры, влагосодержания и давления в выходящем из экструдера материале; уравнения (5) выражают условие осевой симметрии полей t, u и p ; уравнения (6), (7) и (8) выражают условия баланса соответственно теплоты, жидкости и пара на поверхности материала.

В уравнении теплового баланса (6) второе слагаемое соответствует конвективному теплообмену материала с окружающей средой.

где z* – точка на оси z , начиная с которой перенос жидкости не анализируется (эту точку определим позже).

При этом условия однозначности (4)–(8)

примут вид t ।z = z * t ।z = z * -0;

u I _ __ *= u l-_-*

z = z * z = z * — 0

^p L _ .*= ^p l-_-* n;

z = z * z = z * — 0

r = 0

r = 0

I = 0;

r = 0

+ ^{a (} t | r = r ^- t c ) = 0;

^{+ a} p ⁽ p ¹ r = R - p c ) = ⁰-

Уравнения (12)–(15) являются важным частным случаем задачи (1)–(8), поскольку описывают внутренний и внешний тепломассообмен для весьма протяженного участка жгута материала. Однако в дальнейшем для удобства мы будем рассматривать модель тепло- и массообмена в общей формулировке (1)–(8), имеющей силу для любого участка жгута.

Определим для уравнений (1)–(3) степень развития внутренней поверхности парообразования K S , локальную интенсивность j m образования пара (испарения или сублимации) на внутренней поверхности высокопористого материала. При практических расчетах для вычисления j m можно воспользоваться формулами, определяющими интенсивность образования пара на внешней поверхности материала.

В данном случае степень развития поверхности парообразования (или коэффициент) представляет собой отношение совокупной поверхности пор к объему материала:

KS = Sп /V (16)

Здесь задача состоит в том, чтобы вычислить совокупную площадь S п поверхности всех пор в объеме V . Для этого всю пористую структуру материала в объеме V условно представим в виде одной поры, имеющей идеальную цилиндрическую форму, а также объем V э и площадь боковой поверхности S э , равные соответствующим значениям ( V п и S п ) для совокупности всех реальных пор. Такую пору будем называть эквивалентной. Обозначим ее радиус, диаметр и длину соответственно через r э , d э и L э . В таком случае

S п = S э = 2 n r L э . (17)

Здесь в качестве d э = 2 r э можно взять средний диаметр реальных пор (характерный размер пор). Для определения длины эквивалентной поры L э вычислим совокупный объем реальных пор V п . Согласно определению пористости материала П (пористость материала есть отношение объема пор к общему объему материала, т. е. в нашем случае П = V п / V ), имеем

V_n = nV или У П = У э = п г Э L₃ .

Сопоставив последние выражения, получаем L₃ = ПУ /лг2 . Тогда соотношение (17) принимает вид

S_n = — У = — У . r _э d _э

Вспомнив теперь, что K S = S п / V , получаем приближенную формулу для определения степени развития внутренней поверхности парообразования в высокопористом материале:

К

K =

S

В общем случае величины П, d э и, следовательно, коэффициент K S являются переменными по пространству и времени.

В соответствии с тем, что при давлениях выше и ниже тройной точки механизм внешнего массообмена принципиально различается, интенсивность парообразования j m определим отдельно для зоны парового затвора и вакуумированного объема сублимационной камеры.

Для зоны парового затвора, модифицировав известную формулу, положим jm = ^mp 0( Рм - Р) B0 , (19) B где αmp0 – коэффициент влагообмена при нормальном давлении B0 (B0 = = 101,3 кПа), отнесенный к разности парциальных давлений, кг/(м2∙с∙Па); pм – давление пара жидкости (или льда) в рассматриваемой точке материала, Па; B, p – общее (барометрическое) давление и давление пара в пористой среде материала (около рассматриваемой точки), Па. В процессе сушки давление неконденсирующихся газов внутри материала близко к нулю, поэтому можно считать, что B = p.

Для вакуумированного объема сублимационной камеры примем:

j m = O n ⁽ Р м - Р д ), ⁽²⁰⁾

где α m – коэффициент массообмена при вакуум-сублимационной сушке, зависящий от давления p и ряда других факторов, кг/(м²∙с∙Па); p д – давление насыщенного пара при температуре десублимации, Па.

Известно, что в процессе сушки при удалении основной влаги давление пара жидкости (или льда) в материале p м приблизительно равно давлению насыщенного пара свободной жидкости (или чистого льда) p н при температуре материала t и не зависит от его влагосодержания, т. е. Р м = Р н = f ( t) . В период досушки давление пара р м меньше давления насыщенного пара p н и является функцией температуры и влагосодержания материала: р_м = f (t, u) .Эта зависимость такова, что при фиксированной температуре t с уменьшением влагосодержания u давление p м снижается, и, следовательно, снижается интенсивность парообразования. Все это учитывалось при практической реализации рассматриваемой модели.

Для начального периода испарительного замораживания, когда имеет место и анализируется направленный перенос жидкости внутри материала, необходимо определить интенсивность q m 2 испарения жидкости на наружной поверхности жгута. Поскольку, по предположению, образование пара на внешней и внутренней поверхности высокопористого материала происходит по одному закону, то q m 2 определяется так же, как и j m . Для краткости запишем q m 2 = j m I r = R .

Для случая, когда перенос жидкости пренебрежимо мал и не рассматривается, считаем q m 2 = 0.

Общность модели тепло- и массо-обмена (1)–(8) заключается не только в том, что она включает в себя как частный случай задачу (9)–(15), но и в некоторой ее формальности. В этой модели принципиально учтены, но не описаны содержательно такие «элементарные» процессы, как, например, вспучивание материала и образование пористой структуры, кристаллизация жидкости и плавление льда, нагрев материала в поле СВЧ.

Объем и пористость материала в процессе сушки. В нашем случае процесс испарительного замораживания сопровождается вспучиванием материала и образованием у него развитой пористой структуры. Таким образом, при «пористом замораживании» увеличивается объем материала и его пористость, изменяется объемная концентрация сухого вещества. Все это следует учесть при моделировании рассматриваемого процесса сушки.

Увеличение объема материала за счет вспучивания принято характеризовать т. н. коэффициентом взрыва k взр – отношением объема материала после вспучивания к первоначальному объему. Чтобы описать процесс вспучивания в его развитии, введем в рассмотрение переменную величину k V , которую назовем коэффициентом расширения материала и определим как отношение объема материала в рассматриваемый момент времени к первоначальному объему. Очевидно, что в процессе вспучивания коэффициент k V изменяется от 1 до k взр . Задача состоит в том, чтобы установить закон этого изменения.

Между тем, процесс вспучивания при испарительном замораживании довольно сложен, и определение kV путем составления подробного математического описания данного процесса не только затруднительно, но и неоправданно усложнило бы общую модель процесса сушки введением ряда дополнительных трудноопределяемых параметров. Поскольку наша главная задача – описание тепло- и массообмена, то нас вполне устроит предлагаемая далее эвристическая модель вспучивания, основанная на упрощенных представлениях об этом процессе и не использующая никаких дополнительных параметров.

Будем считать, что расширение материала, обусловленное интенсивным испарением влаги, начинается с момента попадания материала в сублимационную камеру (его выхода из экструдера) и заканчивается с началом кристаллизации содержащейся влаги. Так как вспучивание экструдата происходит за счет бурного образования пара, то примем допущение, что скорость расширения экструдированного материала прямо пропорциональна интенсивности парообразования. С другой стороны, в основном интенсивностью парообразования определяется и изменение температуры материала при его испарительном охлаждении. В соответствии с этим будем полагать, что в ходе «пористого замораживания» скорость расширения материала пропорциональна скорости его охлаждения.

В практическом отношении сказанное означает, что для периода вспучивания коэффициент расширения k V линейно зависит от минимальной по объему материала температуры t min , изменяясь от 1 до k взр при изменении t min от начальной температуры материала t 0 до температуры кристаллизации t кр :

^k V = ¹ + ^{( k} взр - 1) t min   ^ 0 , гДе   t min = mln t .

0< r < R tкр   t0

Когда t min достигает значения t кр , начинается кристаллизация влаги, и расширение материала, согласно предположению, прекращается, т. е. коэффициент k V становится постоянным ( k V = k взр ). Значение z , при котором это происходит, обозначим через z кр . Тогда общий вид коэффициента k V следующий:

1 + ( k .

-Q t min    t 0

t кр - t 0

^ПР^И z <  z кр ,

^k взр   ^ПР^И z ^ z кр .

Заметим, что, поскольку при z = z кр завершается формирование пористой структуры материала и содержащаяся в нем влага начинает замерзать, то, начиная с этой точки, внутренним переносом жидкости можно пренебречь. Поэтому введенную в рассмотрение в предыдущем пункте точку z* определим так: z* = z кр .

Определяя изменение линейных размеров объекта сушки, будем предполагать, что при вспучивании расширение жгута материала происходит только в поперечном направлении.

В этом случае коэффициент расширения k V характеризует увеличение в процессе вспучивания площади поперечного сечения жгута S сеч по отношению к площади первоначального сечения (при выходе из экструдера)   S сеч,0 :

. Следовательно,

V       сеч сеч,0 .                              ,       сеч       V сеч,0

или nR2 = kvnR, где R0, R - начальный и текущий радиусы жгута. Из последнего соотношения получаем формулу для определения переменного по z радиуса жгута R:

R = R^ .          (22)

При определении изменения в процессе вспучивания объемной концентрации сухого вещества γ и пористости П примем допущение, что расширение материала происходит равномерно по всему его объему.

Объемная концентрация сухого вещества γ обратно пропорциональна объему материала, поэтому закон ее изменения при расширении материала очевиден:

Y = , (23) kV где γ0 – начальная объемная концентрация сухого вещества, кг сух. вещ./м3.

Определим теперь изменяющуюся в процессе сушки объемную пористость материала П . При этом под пористой структурой будем понимать совокупность всех «пустот» внутри материала, заполненных лишь парогазовой смесью. Рассмотрим некоторый элементарный объем материала V , расширяющийся в процессе вспучивания. Совокупный объем V п всех пор в V складывается из первоначального объема «пустот» V п,0 , объема «пустот» V п,вспуч , образующихся в процессе вспучивания, и объема «пустот» V п,обезв , образующихся в процессе обезвоживания (при удалении влаги освобождается занимаемое ей пространство):

v=V_n+V _ +K , . п п,0 п,вспуч п,обезв

Составляющие V п,0 , V п,вспуч и V п,обезв вычислить несложно:

V o = П 0 V ;

• V„ = V - V o = k v V o - V o = ( k v - 1) V o ;

_v    _ m с ⁽ u o ^- u )_ Y^{V (} u o ^- u )

• V n,o6e3B =                =                  ,

Рв          Рв где П0 – исходная пористость материала; V0 – начальное значение V; mс – масса сухого вещества в объеме V; u0, u – начальное и текущее влагосодержание; ρв – плотность удаляемой влаги (в жидкой или твердой фазе).

Таким образом, для пористости П элементарного объема материала V имеем v V+VV +V .

_п       п,0     п,вспуч     п,обезв

VV

1 (

= - ^ По Vo + (kv - 1)V0 + или, окончательно, yV(uо -u) Рв

П = П 0 + k

k

k V — 1   Y ( u о — ^u )

.

Р в

Нетрудно видеть, что объемная пористость материала П , определенная таким образом, не только зависит от времени пребывания материала в сублимационной камере, но и переменна по радиусу жгута.

Удельное массосодержание льда в процессе сушки. С учетом отмечавшейся выше ничтожной малости массы содержащегося в материале пара по сравнению с массой жидкости или массой льда, влагосодержание материала u в общем случае можно представить в виде u = u2 + u3, (25)

где u 2 , u 3 – удельное массосодержание соответственно жидкой и твердой фазы, кг/кг сух. вещ.

Особенности моделируемого процесса сушки – сложный объемный характер кристаллизации и плавления, неполное замерзание влаги, селективность СВЧ нагрева и другое, – обуславливают необходимость раздельного анализа фаз, допущение о локальной однородности влаги в данном случае неприемлемо. Поэтому, помимо общего влагосодержания u , будем анализировать удельное массосодержание льда u 3 [массосодержание жидкости u 2 при этом тривиально определяется из выражения (25)].

Выходящий из экструдера материал не содержит твердую фазу, поэтому для u3 начальное (или, в условиях квазистационарности, – граничное) условие имеет вид u 3| z=0 = 0. (26)

В дальнейшем, по мере перемещения материала вдоль сублимационной камеры, изменение локального массосодержания льда в нем происходит за счет фазовых превращений лед – жидкость (кристаллизация или плавление) и лед – пар (сублимация или десублимация). В соответствии с этим запишем

duз _ ( duз Л (Цл^^

dz { dz J \ dz J лж лп

Здесь первое слагаемое выражает изменение локального массосодержания льда u 3 за счет фазовых превращений лед – жидкость, а второе – изменение u 3 за счет фазовых превращений лед – пар.

Определение величины ( б u, /8z ) требует разработки специальной модели кристаллизации и плавления, учитывающей особенность протекания этих процессов внутри высокопористого материала, которая заключается в следующем. Движущими силами кристаллизации и плавления в рассматриваемом случае являются соответственно процессы испарения и СВЧ нагрева. Данные процессы носят объемный характер, то есть происходят сразу во всем объеме материала. В соответствии с этим процессы кристаллизации и плавления не развиваются по «классическому» принципу распространения фронта кристаллизации или плавления, представляющего собой четкую границу между влажным и замороженным материалом, а происходят одновременно в некотором объеме материала. Более того, зоны кристаллизации и плавления в общем случае могут чередоваться по радиусу жгута. Таким образом, главным принципом разрабатываемой подмодели должен стать учет локальных условий кристаллизации и плавления (в первую очередь – температуры и массосодержания разных фаз).

Будем предполагать, что процессы кристаллизации и плавления происходят при постоянной температуре t кр . Необходимыми условиями протекания кристаллизации или плавления в некоторой рассматриваемой точке материала будем считать, во-первых, равенство температуры в этой точке температуре t кр : t = t кр и, во-вторых, наличие здесь потенциально замораживаемой жидкости: u <  u - u_H3 (для кристаллизации) или льда: u ₃ >  0 (для плавления). Здесь u_H3 = const - удельное массосодержа-ние незамораживаемой влаги, кг/кг.

Процессы кристаллизации и плавления протекают соответственно с выделением и поглощением теплоты. В уравнении теплопроводности (1) это учитывается с помощью слагаемого (внутреннего источника теплоты) Q кр , которое с учетом наших обозначений определяется следующим образом:

Q кр = 4 р Y V М I , (28) лж

Если в рассматриваемой точке материала

происходит кристаллизация или плавление, то, по крайней мере, в течение бесконечно малого промежутка времени температура в этой точке, по предположению, постоянна ( t = t кр ). Следовательно, учитывая квазистационарность процесса: dt/ д z = 0.

Подставляя это условие в (29), получаем уравнение теплового баланса в точке кристал-

лизации или плавления:

1дГ д 11

--1 АГ— I r дr \ дr J

^{- Г} с Jm^KS + ^Г кр Y v

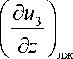
+ Q CB4

= 0,

откуда

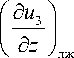
-----X гкр Yv

■ 1 дГ  д 11

-^IAr^-1 r д r ^   д r J

^Г с JmKS + Q CB4

Формулой (30) можно пользоваться

для определения величины

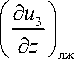
только

в том случае, когда в рассматриваемой точке материала выполняются оговоренные выше необходимые условия кристаллизации или плавления. Чтобы определить данную величину в общем виде, обозначим правую часть соотношения (29) через F :

F = -

X

^г кр Y v

' 1 д Г д 11 -—I Ar— I r д r ^ д r J

r JmKS + Q CB4

Тогда, исходя из очевидных физических соображений, общее определение искомой величины можно сформулировать следующим образом:

F при F >  0, t = t , кр ,

где r кр – удельная теплота кристаллизации, Дж/кг.

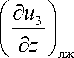
Тогда уравнение теплопроводности принимает вид

д t

CYV--= дz

■ „   ,         I диз I п

- ^Г с j_mKS + ^Г кр Y v I      I + Q СВЧ .

I дz Jлж

u <  u - u_m 3            нз

(кристаллизация);

F при F <  0, t = t кр , ^u 3 >  ⁰ (плавление);

0 во всех остальных случаях.

Таким образом, если в рассматриваемой точке материала u ₃ >  0, то в этой точке изменение массосодержания льда за счет фазовых

превращений лед – пар количественно совпадает с изменением общего влагосодержания за счет парообразования:

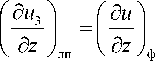
При u ₃ = 0 сублимация льда, естественно, не происходит; случай десублимации рассматривать не будем, поэтому

du 1  = 0.

I dz

Таким образом, общий вид второго слагаемого соотношения (27):

ди 3 ] dz J лп

—m-S- при щ >  0;

‘ Y                      (33)

0 при и ₃ = 0.

Заметим, что, в соответствии с выражением (33), удельная теплота парообразования rс может быть представлена в виде rс

' А   ^пр^{и и} з > 0;

. Ап   при ^и 3 = 0,

)

где r исп , r суб – удельная теплота соответственно испарения и сублимации, Дж/кг.

Итак, мы определили формулой (28) слагаемое Q кр уравнения теплопроводности (1) и разработали математическую модель (26), (27), (32), (33), позволяющую определить локальное массосодержание твердой фазы u 3 с учетом его изменения в процессе сушки за счет кристаллизации жидкости, плавления и сублимации льда.

Моделирование СВЧ нагрева. Энергия сверхвысокочастотного электромагнитного поля, проникая в толщу материала, трансформируется в теплоту во всем объеме этого материала. СВЧ нагрев, таким образом, в принципе подобен введению в материал внутреннего источника тепла, поэтому в нашем случае он учитывается в уравнении теплопроводности (1) с помощью специального слагаемого Q СВЧ .

Для зоны воздействия СВЧ поля:

О СВЧ = 0,556 - 10 ^{- 10} £”v E 2 , (34) где s" = £^r tg ^ - коэффициент диэлектрических потерь; е’ - диэлектрическая проницаемость; д - угол диэлектрических потерь; v - частота электромагнитных колебаний, Гц; E – напряженность электрического поля, В/м.

Вне зоны действия СВЧ поля Q СВЧ = 0.

Обозначим через z 1 и z 2 соответственно начало и конец зоны воздействия на материал поля СВЧ. Тогда общее определение удельной мощности Q СВЧ внутреннего источника теплоты, связанного с СВЧ нагревом, выглядит следующим образом:

Q CB4

0,556 - 10 ^{- 10} sV E ²

при Zj < z < z2;

0 при z < Zj или z > z2.

Так как в рассматриваемом процессе сушки характерный размер материала (радиус жгута R) сравнительно мал и, кроме того, материал обладает высокой пористостью, то с высокой степенью достоверности можно считать, что напряженность СВЧ поля E постоянна по объему сушимого материала, т. е. электромагнитные волны не затухают при про- хождении от поверхности жгута к его центру.

Вместе с тем, при моделировании СВЧ нагрева обязательно следует учесть селективность поглощения электромагнитной энергии различными составляющими влагосодержащих материалов – сухой основой, жидкой и твердой фазой влаги, паром и т. д. Так, коэффициент диэлектрических потерь воды весьма велик и значительно превышает соответствующие значения для сухой составляющей большинства материалов. При этом замороженная влага почти не поглощает энергию СВЧ поля, а коэффициент диэлектрических потерь пара практически равен нулю. Поскольку в процессе сушки концентрация разных составляющих материала (в первую очередь – жидкой и твердой фазы влаги) изменяется, то в нашем случае значение общего коэффициента диэлектрических потерь материала е" может на целые порядки различаться по радиусу и, особенно, по длине жгута. Поэтому значение е” должно определяться с учетом соответствующих условий (температуры, состава материала и прочего) в каждой конкретной точке объекта сушки. Лишь так при моделировании можно учесть не только объемный, но и адресный характер СВЧ нагрева.

Проблема здесь состоит в том, что экспериментальное определение сложной зависимости коэффициента е" от состава, структуры, температуры материала и прочих факторов довольно трудоемко и не может гарантировать получения достаточно точных результатов. В связи с этим предложим способ упрощенной аналитической оценки зависимости е'' от состава и структуры материала.

Будем условно считать, что сушимый материал состоит из четырех компонентов – сухого вещества, воды, льда и пара, заполняющего поры («пустоты»). В соответствии с этим общий коэффициент ε'' представим в виде суммы коэффициентов диэлектрических потерь каждого из компонентов, умноженных на некоторые весовые коэффициенты:

с"=ос"+осв+оХ+^Х (36)

где с", с", с", с" - коэффициенты диэлектри- ческих потерь соответственно для сухого вещества, воды, льда и пара; σс, σв, σл, σп – весовые коэффициенты. Все весовые коэффициенты неотрицательны, их сумма равна единице.

Так как удельная мощность СВЧ нагрева Q СВЧ рассчитывается по объему материала, то каждый из весовых коэффициентов целесообразно определить как отношение объема соответствующего компонента к общему объему материала. Это позволит также учесть высокую пористость материала, которая снижает его способность поглощать энергию поля СВЧ.

Рассмотрим внутри материала некоторый элементарный объем V. Обозначим через Vс, Vв, Vл и Vп соответственно объем сухого веще- ства, жидкости, льда и заполненных паром пор в объеме V. Имеем mсγ ρсV  ρс

σ _с

σ _в

V с V

V в V

mmu γ

—- =   2 = —( u - u ₃);

ρV ρV ρ ввв

Vл   mл   mсu3

=   =    ==

V  ρл V  ρл V  ρл

σ _п

V п V

= П ,

где m с , m в , m л – масса сухого вещества, жидкости и льда в объеме V , кг; ρ с , ρ в , ρ л – плотность сухого вещества, жидкости (воды) и льда, кг/м³.

С учетом того, что пар практически не поглощает электромагнитную энергию ( с" = 0), окончательно получаем

с" = ^с" + Y(u - и)с" + Yис".  (37)

ρ _с     ρ _в           ρ _л

Диэлектрические характеристики воды и льда с их зависимостью от температуры хорошо изучены. Формула (37) позволяет также учесть зависимость коэффициента диэлектрических потерь материала от объемной концентрации сухого вещества и локального массосодержа-ния жидкости и льда.

Заключение

В представленной статье разработана комплексная математическая модель, описывающая процесс вакуум-сублимационной сушки высокопористого материала с использованием сверхвысокочастотного (СВЧ) нагрева. Модель основана на системе дифференциальных уравнений в частных производных, учитывающих взаимосвязанные процессы теплопроводности, массопереноса, парообразования, фазовых переходов и объемного энергоподвода.

Ключевым достижением работы является синтез общей модели из ряда специализированных подмоделей, каждая из которых детально описывает отдельный аспект процесса: тепло-и массообмен, изменение структуры, фазовые переходы, СВЧ-нагрев.

Основным теоретическим выводом является демонстрация принципиальной возможности адекватного математического описания столь сложного технологического процесса, характеризующегося интенсивным нестационарным тепло- и массообменом, значительными изменениями структуры материала и одновременным протеканием разнонаправленных физических явлений. Предложенный подход, основанный на разделении процесса на элементарные составляющие, показал свою эффективность для построения целостной модели.

Практическая значимость модели заключается в том, что она создает теоретическую основу для:

– проведения виртуальных экспериментов и анализа влияния различных технологических параметров (скорости движения материала, мощности СВЧ-поля, условий в камере) на ход сушки;

– оптимизации режимов работы сушильной установки с целью интенсификации процесса, снижения энергозатрат и предотвращения перегрева продукта;

– определения рациональных конструктивных параметров оборудования.

Таким образом, представленная работа вносит существенный вклад в теорию сушки капиллярно-пористых материалов в энергетических полях и предоставляет ценный инструментарий для инженерных расчетов и проектирования современных вакуум-сублимационных установок с СВЧ-дополнительным нагревом. Дальнейшим развитием исследования может стать численная реализация модели, ее верификация экспериментальными данными и уточнение эмпирических коэффициентов для конкретных видов материалов.