Моделирование процесса вакуум- сублимационной сушки гранулированных продуктов

Одним из направлений интенсификации вакуум-сублимационной   сушки является увеличение поверхности испарения путем организации процесса сушки в тонком слое. Развитием этого направления служит метод, основанный на удалении высохшего слоя продукта с поверхности гранул, образованных в виде сферических тел и помещенных в перфорированный барабан.

После процесса предварительного замораживания гранулы попадают в расположенный в вакуумной сушильной камере перфорированный барабан, где образуют слой высоты h (рисунок 1).

S A

Зона A Zone A Зона B Zone B

d

l

Рисунок 1. Поверхностный и глубинный слой гранул (зоны A и B)

Figure 1. The superficial and the deep layer of the pellet (zone A and B)

Гранулы, находящиеся на поверхности слоя, прогреваются постоянным инфракрасным излучением плотности q . Барабан вращается, поэтому гранулы постоянно перемешиваются, и энергия теплового излучения более-менее равномерно распределяется на все гранулы. За счет такого теплоподвода происходит процесс сублимационной сушки продукта, в результате чего на поверхности гранул за некоторый малый период времени образуется слой сухого продукта (рисунок 2).

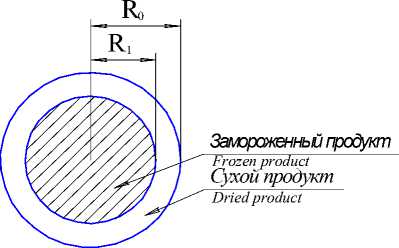
Рисунок 2. Замороженная гранула продукта с его сухим слоем

Figure 2. The frozen pellet of the product with its dry layer

При постоянном перемешивании гранул продукта за счет трения их между собой и о стенки барабана сухая часть продукта претерпевает деструкцию и равномерно отделяется от замороженного остатка. Процесс заканчивается тогда, когда весь продукт в грануле превращается в сухой порошок, т. е. сухой слой продукта полностью разрушается, сухие частицы продукта измельчаются под воздействием сил трения между собой и о цилиндрическую сетку поверхности вращающегося барабана до размеров перфорированной сетки и просыпаются через ее ячейки в разгрузочный патрубок.

Для построения адекватной модели описанного выше процесса сушки, целесообразно рассматривать отдельную гранулу, а не слой гранул в целом, но с учетом влияния гранул друг на друга в процессе сушки.

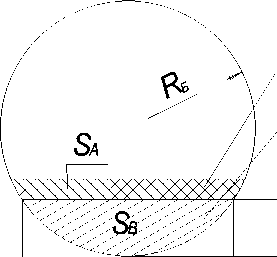
При сушке гранулированного продукта во вращающемся барабане тепловым излучением прогреваются только гранулы, находящиеся на поверхности слоя (ниже инфракрасные лучи не проникают). За счет вращения барабана каждая гранула попеременно оказывается то на поверхности слоя, то в его глубине. Таким образом, воздействие лучистого потока на гранулу носит переменный характер. Поэтому весь слой гранул целесообразно разделять на две области – поверхностный слой (зона A ), высота которого равна диаметру гранулы и глубинный слой (зона B ) (рисунок 1). Каждый раз длительность пребывания гранулы в зоне A или, соответственно, в зоне B различна и, вообще говоря, случайна. C учетом отмеченных выше факторов гранула равномерно со всех сторон облучается тепловым потоком плотности:

q = 9 _T 9 s q . (1)

где q – плотность лучистого потока, реально падающего на гранулы поверхностного слоя. Коэффициент θ τ служит для учета прерывистого характера облучения гранулы, 0 ≤ θ τ ≤ 1. С помощью коэффициента θ S учитывается односторонность облучения гранулы, 0 <  9 S < ^.

В связи с определением θ τ предложим два альтернативных подхода. Первый из них основывается на допущении, что благодаря вращению барабана энергия теплового излучения, в конечном счете, равномерно распределяется между всеми гранулами. Поэтому будем условно считать, что в каждый момент времени облучаются не только гранулы, находящиеся на поверхности слоя (в зоне A ), а вообще все гранулы в барабане. Следовательно, энергия, которую получают реально облучаемые в данный момент гранулы, должна быть равномерно распределена на все гранулы. В соответствии с этим подходом коэффициент θ τ мы должны положить равным отношению объема, занимаемого зоной A к объему всего слоя гранул или, что то же самое, отношению площади S A поперечного сечения зоны A к сумме S A + S B площадей поперечных сечений зон A и B (рисунок 3):

9 = —SA— ^Т   S a + S b

S a » ld = 2 d V ^ s - ( R_Б - h + d ) ² ,

S B

= R 2 arccos Б

R_Б - h + d

R Б

-

- ( R_Б - h + d )V R Б - ( R_Б - h + d ) ² .

где R Б – радиус барабана; d – высота зоны A, d ≈ 2 R 0 ( R 0 – начальный радиус гранулы); l – ширина зоны A; h – высота слоя гранул.

При втором подходе к определению θ τ предположим, что, попадая при вращении барабана в какую-либо из зон A и B , гранула каждый раз пребывает в этой зоне приблизительно равные периоды времени. Пусть τ A и τ B – средняя продолжительность пребывания гранулы в зоне A и B соответственно (промежуток времени между моментом попадания гранулы, соответственно, в зону A или B и моментом ее перехода в другую зону). Тогда моделируемый процесс можно приближенно представить в виде циклической смены двух фаз, каждая из которых имеет постоянную длительность. Первая фаза – пребывание гранулы в зоне A (под облучением), ее длительность – τ A . Вторая фаза – пребывание гранулы в зоне B (без облучения), длительность – τ B . Таким образом, четко различаются два состояния гранулы – она либо облучается, либо не облучается. Отсюда коэффициент:

1, если гранула пребывает в зоне A

⁹ t = {

(I фаза цикла),                         (3)

0, если гранула пребывает в зоне B

(II фаза цикла).

Здесь коэффициент θ τ дискретным образом зависит от времени и определяется длительностями фаз τ A и τ B , которые в сумме составляют продолжительность цикла и являются параметрами модели. Эти параметры зависят от размера гранул, а также от загруженности и скорости вращения барабана. Причем достаточно знания лишь одного из этих параметров, второй же может быть определен из пропорционального соотношения:

^t a = S a

^T B    S B

где S A и S B – как и прежде, площади поперечных сечений зон A и B соответственно.

Следует также отметить, что первый способ определения θ τ является предельным случаем второго, когда параметры τ A и τ B , связанные соотношением (4), совместно стремятся к нулю.

Для определения коэффициента θS из формулы (1), служащего для учета односторонности облучения гранулы предположим, что с какой-либо стороны на гранулу падают параллельные тепловые лучи. Очевидно, что под облучение попадет в точности половина поверхности гранулы. Однако бóльшая часть потока излучения, падающего на поверхность гранулы под очень острым углом, будет отражена. Поэтому, целесообразно условно сократить облучаемую поверхность до некоторой области поверхности, которая образуется сектором сферы, определяемым углом φ, 0 < φ ≤ π/2 (рисунок 3). Эту область назовем областью эффективного облучения и обозначим через Sφ.

Излучение

Emitting

S ,

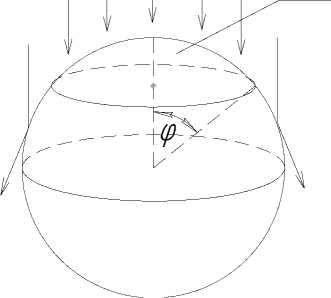
Рисунок 3. Схема облучения поверхности гранулы

Figure 3. The scheme of irradiation of the surface of the pellets

Чтобы поток излучения, падающий на область S φ , равномерно распределить на всю поверхность гранулы, коэффициент θ S , очевидно, следует положить равным отношению площади S φ к площади S всей поверхности гранулы. Если R – текущий радиус гранулы, то имеем:

S ^    2 n R ² (1 - cos ^ ) 1 - cos ф

= S ”    4 Л к ²    ”  2

Так как лучи, падающие на гранулу под острым углом, почти не отражаются ею, в качестве φ следует взять значение, близкое к π/2.

В процессе сублимационной сушки фронт сублимации продвигается от поверхности гранулы вглубь. [6] Он разделяет общий объем продукта на две части, существенно отличающиеся механической прочностью. Поверхностный высохший слой легко разрушается.

Учитывая геометрическую форму гранулы, наше рассмотрение будем проводить в сферической системе координат, поместив начало координат в центр гранулы. С учетом сделанных ранее предположений наша задача, очевидно, является осесимметричной. Ее математическая постановка выглядит следующим образом:

d T   1 д Г 2 d T ) „ c 2 p 2=       1 22 r       1 + Q2, дт   r дr ^     дr J

R н <  r <  ^ ( т ), т >  0,

T2(r,0) = Тсуб = const,(7)

^,т) = Туб,(8)

, д Т ₂( ^ , т)      _n d^ ( T )

Л>           = Yсуб p2        , д rd

^(0) = R0, Rн < §(т) < Rо,(10)

где T 2 ( r, τ ) – температурное поле продукта, K; c 2 ( T ) – удельная теплоемкость продукта, дж/кг⋅град; ρ 2 ( T ) – плотность продукта, кг/м ³ ; λ 2 ( T ) – коэффициент теплопроводности продукта, вт/м⋅град; Q 1 ( r, τ ), Q 2 ( r, τ ) – мощность внутренних тепловых источников (вопрос о функциях Q 2 обсуждается ниже), вт/м ³ ; T суб – температура сублимации, K; γ суб – теплота сублимации, дж/кг; ξ ( τ ) – положение фронта сублимации, м; R 0 – начальный радиус гранулы, м; R Н – радиус фронта сублимации, м; τ – время, с; r – пространственная координата, м .

Задача (6)–(10) представляет собой одномерную параболическую краевую задачу с подвижной границей. Она включает в себя нестационарные уравнения теплопроводности (6), начальное условие (7), граничные условия (8)–(10) и определяющие подвижную границу условия (13), (14). Искомыми величинами здесь являются температурное поле T 2 и свободная граница ξ .

Граничное условие (9) является условием симметрии, условие (8) – условием постоянства температуры в зоне сублимации. Уравнение (9) является условием баланса энергии на фронте сублимации, оно определяет динамику распространения фронта сублимации и в совокупности с условием (10) позволяет установить положение этого фронта в различные моменты времени.

Согласно [5], учитываем энергию теплового излучения введением в уравнение теплопроводности функций внутренних тепловых источников Q 2 .

При падении потока излучения F на поверхность тела в общем случае могут наблюдаться явления зеркального и рассеянного отражения и преломления на границе тела и среды, а также явления рассеяния и поглощения в толще тела, что приводит к соответствующему ослаблению и пропусканию. Таким образом:

F = Fa + Fp + Fy , где Fα , Fβ , Fγ – соответственно отраженная, поглощенная и пропущенная телом части потока F.

Согласно [2], для параллельных лучей коэффициент пропускания γ имеет вид:

,       - kx

Y = e , где x – расстояние, пройденное лучами в толще материала, м; k – коэффициент ослабления (или показатель поглощения), характеризующий относительное изменение интенсивности излучения на единицу длины пути в поглощающей и рассеивающей среде, 1/м.

Мощность Q ( вт/м ³) теплового источника, связанного с поглощением тепловых лучей, следуя [5], определим формулой:

Q ( x ) = Q o e - kx . (11)

Выражение (11) является аналогом закона ослабления (поглощения) Ламберта-Бугера [1, с. 23].

Определим коэффициент Q 0 в формуле (11). Очевидно, что эта величина не может зависеть от размеров тела, поэтому при ее определении будем рассматривать тело толщины l = ∞. Это избавляет нас от необходимости учета пропущенного (непоглощенного) телом излучения, так как все неотраженные лучи полностью поглощаются.

Пусть q – плотность лучистого потока ( Вт/м ²), падающего на поверхность тела, а q α и q β – соответственно плотность отраженного и поглощенного телом излучения. Тогда:

q = q _a + q _P . (1²)

Если α – коэффициент отражения для поверхности тела, то из (12) получаем:

q _P = q ^- q « = q ^- « q = ^{(1 - a} ) q .     (13)

С другой стороны, энергия поглощенного теплового излучения распределяется в толще тела по закону (11). Поэтому плотность q β лучистого потока, поглощенного телом, можно определить интегрированием выражения (11) по интервалу (0, ∞):

r_ Q£1 1₊ S o = e, . (14)

( k J k k to qe = f Q0 e - kxdx = lim

^    3                 a -^to

Сопоставив выражения (13) и (14), получаем: (1 - a)q = ^y0-, k откуда:

Q 0 = k (1 - a ) q .

Общий механизм взаимодействия тепловых лучей с гранулой следующий. Часть падающего излучения отражается поверхностью слоя продукта. Неотраженное излучение проникает вглубь этого слоя и здесь, согласно закону поглощения Ламберта–Бугера, поглощается.

Поэтому на основании формул (11) и (15) мощность теплового источника, связанного с поглощением инфракрасного излучения, для продукта определим следующим образом:

Q 2 ( r , t ) = k 2 (1 - a ₂) qe - ^{k 2}( ^{5 ( T} ) - r ⁾ +

+ k 2 a 1 (1 - a ₂) q e - ^k 2 ^{( 5 ( T} ) - R н ) e - ^k 2 ^{( r} - R н ) ,

R _Н < r ≤ ξ ( τ ),