Моделирование процесса высокочастотного нагрева влажной древесины в вакуумно-диэлектрической сушильной камере

Введение . Диэлектрический нагрев в высокочастотном (далее ВЧ) электромагнитном поле получил широкое применение в промышленности благодаря более высокой скорости нагрева по сравнению с конвективным, кондуктивным и радиационным способами подведения тепла, а также одновременному повышению температуры во всем объеме тела.

Особое положение высокочастотный диэлектрический нагрев занимает при обработке древесины. Сушка стала одной из первой областей его промышленного применения. Впоследствии развитие получили конвективно-диэлектрические и вакуумно-диэлектрические (далее ВД) сушильные камеры [1]. Последние с точки зрения качества и скорости сушки более предпочтительны, но имеют общий недостаток – большой разброс конечной влажности из-за неравномерного распределения внутренних источников теплоты и, как следствие, неравномерного нагрева [2]. Причина неравномерности состоит в возникновении в рабочем конденсаторе волновых процессов, которые зависят от соотношения габаритов загрузки и частоты источника, а также диэлектрических свойств древесины.

Цель исследования : изучение влияния параметров высокочастотного источника и свойств загрузки на равномерность нагрева.

Для достижения данной цели необходимо решить следующие задачи : разработать математическую модель, описывающую ВЧ-нагрев материалов с анизотропными переменными свойствами с учетом волновых процессов; ис-

ВД-камере, изображенной на рисунке 1. При вертикальном расположении электродов 1 штабель формируется из горизонтальных рядов досок 2, укладываемых через прокладки 3. Если электроды максимально плотно прилегают к штабелю, а вертикальные промежутки между досками (шпации) отсутствуют, то в силу ортогональности электродов и границ раздела дре- следовать полученную модель.                  весина-воздух напряженность электрического

Методы и результаты исследования . Рас- поля E , В/м, в каждом слое должна быть одина-смотрим особенности ВЧ-нагрева древесины в ковой и равной:

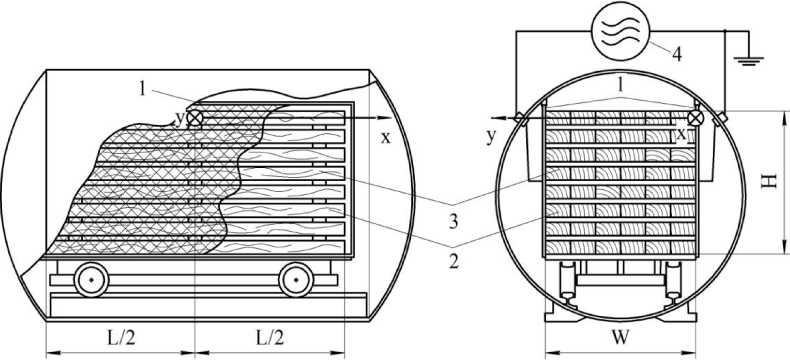
Рис. 1. Конструкция вакуумно-диэлектрической камеры и выбор системы координат:

1 – электроды; 2 – пиломатериал (доски); 3 – прокладки; 4 – высокочастотный генератор

E = U ,

W

где U – выходное напряжение генератора, В; W – расстояние между электродами, м. Однако электромагнитное поле не является однородным, что обусловлено волновыми явлениями. Наиболее ярко это проявляется по длине штабеля, которая обычно составляет 6÷6,5 м и соизмерима с длиной электромагнитной волны λ во влажной древесине. Волновой характер распределения E описывается дифференциальным уравнением Гельмгольца [3]. Пренебрегая изменениями ЭМП по ширине и высоте штабеля, перепишем его в одноразмерной форме с учетом выбранной системы координат (см. рис. 1):

^E - k ²( x ) E = о , (2) dx²

где k – (волновой) коэффициент распространения электромагнитной волны, 1/м. В (2) учтено, что волновой коэффициент неоднороден и зависит от диэлектрических свойств древесины, которые являются функциями температуры и влагосодержания, а последние зависимы от координаты:

s( x) = ^(T ( x), u ( x )),tg^( x) = tgd(T ( x), u ( x)), k (x) = j • 2я • fJ £ оИо^( x XI - j • tg£( x)), где f – рабочая частота генератора, Гц; ε0, μ0 – абсолютные диэлектрическая и магнитная проницаемости вакуума; ε – относительная диэлектрическая проницаемость; δ – угол диэлектрических потерь; T – температура, oС; u – влаго-содержание, кг/кг. Принимаем, что токопроводы подключены к электродам по центру. В точке подключения задаем граничное условие [4], коэффициент перед E принимаем равным единице:

^ESS = k (0) ( E (0) -1 • Eo), (3) ex где E – амплитуда падающей волны, В/м, определяется по (1). На границе справа ставим условие симметрии:

d E ( L /2) ----------= U .

∂ x

Правое граничное условие найдено авторами эвристически. Решив задачу (2)–(4), находим функцию E ( x ) и получаем распределение удельной мощности тепловой энергии, Вт/м³, выделяющейся в материале:

Q v = 2л f g _o f (x)tg ^ ( x ) E ( x )| ² .   (5)

При нагреве внутри влажной древесины начинают происходить процессы тепломассопе-реноса, описываемые системой уравнений А.В. Лыкова [5], решение которой известно своей сложностью. Для упрощения считаем, что нагрев происходит гораздо быстрее, чем изменение поля влагосодержания, т. е. распределение влагосодержания в древесине равномерно и одинаково в любой момент времени. Это позволяет не учитывать перекрестные эффекты тепломассопереноса. Если начальное влагосо-держание одинаково во всем штабеле, то одинаковой будет картина электромагнитного поля в каждом ряде досок, тогда процесс нагрева достаточно рассмотреть только для одного ряда. Электромагнитное поле симметрично относительно точек подключения, поэтому симметричным будет и температурное поле. С учетом этого тепловая задача описывается дифференциальным уравнением теплопроводности с внутренними источниками тепла (6), дополненным граничными условиями симметрии (7) и конвективного теплообмена (8)–(10), а также начальными условиями (11) и (12):

d T ( x , y , t)_ d          d T ( x , y ,t)

с(T, u)p(T, u)    n      = ^ (Xx (T, u)     ~)

∂τ∂

• + ^ (Xy (T, u) dTiWL) + Q^ (x) ,

∂ y ∂ y

• X x (T, u)dT(O, y ’T) = 0,

∂ x

X x (T , u) L TAL^yEl = a(T)(T ( L1 2, y ,_T) - T cp ) ^{, (8)} ∂ x

• - X y ( T , u ) ^{dT ( x ,0, t)} = a( T )( T ( x ,0,t) - T_cp) , ⁽⁹⁾ ∂ y

Xy (T, u) VTxBlL = a(T)(T(x, B,t) - Tcp) ’

∂ y

T (x, y ,0) = To = const,(11)

u (x, y, t) = u0 = const,(12)

где с – теплоемкость, Дж/(кг∙^oС); ρ – плотность, кг/м³; τ – время, с; λ x и λ y – теплопроводность древесины вдоль и поперек волокон соответственно, Вт/(м∙^oС); α – коэффициент конвективного теплообмена, Вт/(м²∙ ^oС); T ср – температура окружающей среды, ^oС; T 0 – начальная температура материала, ^oС; u 0 – начальное влаго-содержание древесины, кг/кг.

Совместная задача (2)–(12) решалась методом конечных разностей с использованием чисто неявной локально-одномерной схемы, построенной интегро-интерполяционным способом [6]. Моделирование производилось для штабелей длиной L = 6 м, шириной W = 1 м при значении выходного напряжения генератора 5 кВ на частотах 1,78 и 13,56 МГц. Порода древесины – сосна с базисной плотностью 400 кг/м³ и с начальным влагосодержанием 0,12 и 0,6 кг/кг. Числа узлов пространственной сетки приняты равными N x = 40 и N y = 40, временной – N τ = 100, время нагрева – 30 мин. Функциональные зависимости теплофизических свойств сосны от температуры и влагосодержания получены путем интерполяции по данным [7], а диэлектрических свойств – по данным [8]. Коэффициент конвективного теплообмена, в соответствии с [4], принят равным 5 Вт/(м²∙^oС). Результаты вычислений приведены на рисунках 2 и 3.

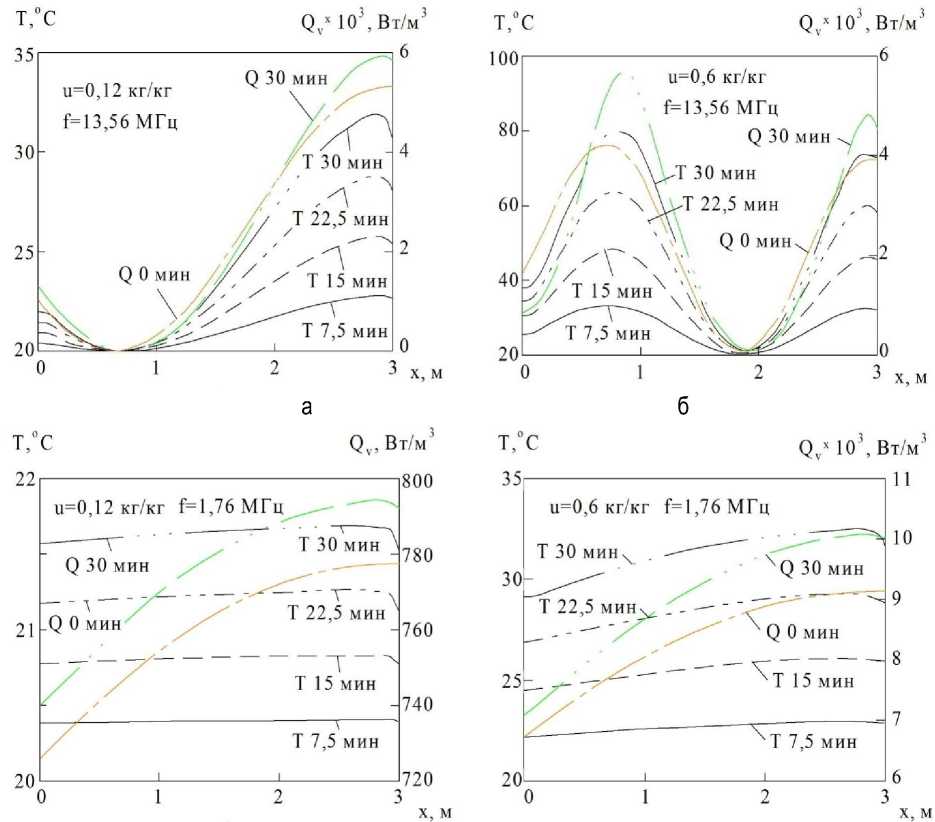
На рисунке 2 прослеживаются основные закономерности высокочастотного нагрева. Максимальная скорость нагрева наблюдается при частоте генератора 13,56 МГц (рис. 2, а, б), минимальная – при частоте 1,76 МГц (рис. 2, в, г). С повышением влажности эта скорость еще больше возрастает, так как коэффициент диэлектрических потерь £• tg ^ для сосны с вла-госодержанием 0,12 и 0,6 кг/кг отличается более чем в 10 раз. Во всех случаях скорость нагрева изменяется незначительно на протяжении всего расчетного времени, а ее средние значения находятся в диапазоне от 0,054 ^oС/мин (рис. 2, в) до 1,8 ^oС/мин (рис. 2 б).

Распределение внутренних источников теплоты, а следовательно, и температуры наиболее равномерно при частоте 1,76 МГц. На характер распределения в большей степени оказывает влияние влажность, поскольку с ее ростом увеличивается коэффициент затухания Re ( k ). При влагосодержании 0,12 кг/кг разница между максимальной и минимальной температурами через 30 мин составляет 0,11 oС (рис. 2, в), а при 0,6 кг/кг – 3,1 oС (рис. 2, г). Температура несущественно сказывается на характере распределения источников тепла, но влияет на их величину. Например, через 30 мин нагрева на частоте 1,76 МГц температура в точке x = 2 м

в

г

Рис. 2. Распределение температуры и мощности внутренних источников теплоты по длине штабеля при y = B/2 в разные моменты времени при нагреве на частотах 1,76 и 13,56 МГц и влагосодержании древесины 0,12 и 0,6 кг/кг

Неравномерный нагрев характерен для частоты 13,56 МГц, при которой по длине рабочего конденсатора возникают узлы и пучности напряжения. Это приводит к тому, что в древесине образуются полностью непрогретые области (рис. 2, а, б), а разница между максимальной и минимальной температурами через 30 мин достигает Δt = 62,4 oС (рис. 2, б). Такое явление может служить причиной механических деформаций и повреждений пиломатериала в поднялась на 12 oС, мощность внутренних источников теплоты при этом увеличилась на 11 % (рис. 2, в). Однако при достаточно большом изменении температуры максимум Qv смещается относительно начального положения (рис. 2, б).

процессе сушки. Чтобы снизить неравномерность, рекомендуется подключать электроды к высокочастотному генератору 4 (рис. 1) в нескольких точках [3]. Для изучения этого эффекта авторами разработана соответствующая модель. Результаты вычислений нагрева штабеля с влагосодержанием 0,12 кг/кг на частоте 13,56 МГц при подключении в трех точках показаны на рисунке 3. Точкам подключения соответствуют координаты x = 0 м и x = 2 м. Из ана- лиза результатов следует, что величина Δt сократилась до 22,3 oС, т.е. нагрев стал более равномерным, но этого недостаточно для качественной сушки. Дальнейшее увеличение числа точек подключения приводит к усложне- нию конструкции вакуумной камеры, поэтому для обеспечения равномерности в данном примере следует выбрать частоту 5,28 МГц (Δt = 1,3 oС при u = 0,12 кг/кг и Δt = 12,9 oС при u = 0,6 кг/кг).

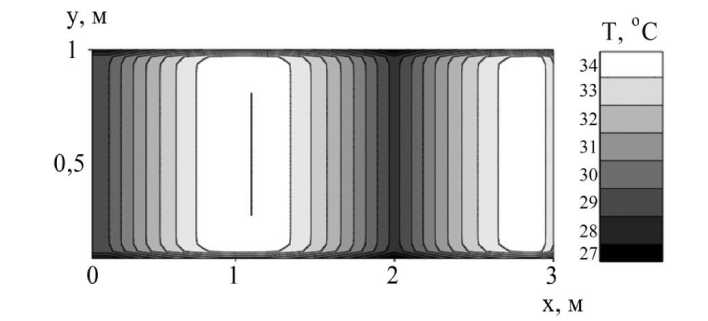
Рис. 3. Температурное поле при нагреве на частоте 13,56 МГц и при подключении электродов в 3 точках

Для анализа процессов диэлектрического нагрева разработано множество математических моделей. Общим для них является использование уравнения теплопроводности Фурье. Особенности каждой модели заключаются в распределении внутренних источников теплоты. В одних процессах ВЧ-нагрева электрическое поле можно считать однородным [9], тогда напряженность электрического поля находится по формуле (1), в других – квазистационарным, тогда применяется уравнение Лапласа [10]. Необходимость учета волновых явлений обычно возникает в задачах СВЧ-нагрева [11], для которых решение может быть получено разными способами, в том числе и путем численного расчета уравнения Гельмгольца, но специфика

СВЧ-энергии заставляет применять иные граничные условия. В нашем случае для сравнения наиболее подходит закон распределения, известный из [12]:

E ( x ) = E o COs(P(L _x /2- x )) , (13)

где в = Im( k ) - коэффициент фазы, 1/м.

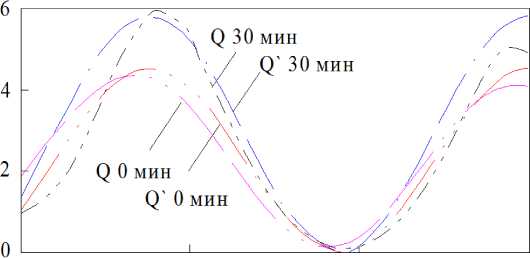
Расчет системы (5)–(13) проведен при влажности 0,6 кг/кг и частоте 13,56 МГц. На рисунке 4 показаны кривые распределения источников теплоты в начальный момент времени «Q`0 мин» и в конце нагрева «Q`30 мин». Для удобства анализа здесь также воспроизведены кривые «Q0 мин» и «Q30 мин» рисунка 2, б.

Q/ 103,Вт/м3

1                      2                      3

Рис. 4. Результаты расчетов предлагаемой модели (2)–(12) и ранее известной модели (5)–(13)

X, м

В целом система (5)–(13) дает схожий результат, но для возможности использования (13) необходимо усреднять диэлектрические свойства материала по всему объему на каждом шаге по времени, что вносит погрешность в расчет. Дополнительная погрешность возникает из-за того, что (13) опускает действительную составляющую волнового коэффициента а = Re( k ) , т. е. затухание электромагнитной волны не учитывается. Особенно сильно это проявляется на свободном краю конденсатора ( x = 3 м), где расчетные значения в конце нагрева отличаются на 20 % (рис. 4).

Выводы . На основании изложенного материала можно сделать следующие выводы:

– предложена математическая модель, представляющая собой связанную нестационарную задачу электродинамики и теплопроводности в среде с анизотропными температу-ро- и влагозависимыми свойствами, описывающая ВЧ нагрев древесины в ВД камере с учетом волновых процессов;

– модель может быть использована для исследования иных процессов ВЧ нагрева различных длинномерных материалов в плоских конденсаторах без воздушных зазоров;

– модель позволяет выбрать оптимальные напряжение и частоту генератора, обеспечивающие достаточную равномерность и высокую скорость нагрева при безопасном для материала значении напряженности электрического поля;

– исследование полученной модели показало, что равномерность температуры по длине штабеля достигается на частоте 1,76 МГц, однако скорость нагрева низка; при длине штабеля соснового пиломатериала 6 м рационально проводить нагрев на частоте 5,28 МГц; на частоте 13,56 МГц скорость максимальна, но температура неоднородна даже при подключении электродов в нескольких точках.