Моделирование процессов фильтрации растворов солей тяжелых металлов и биосурфактанта в почве

Тяжелые металлы, попадающие в окружающую среду в результате производственной деятельности человека, являются опасными загрязнителями биосферы. Они попадают в природную среду различными промышленными и бытовыми способами: в результате обработки металлов, изготовления металлоконструкций, производства краски, удобрений, вывоза отходов, сжигания топлива и т. д. [8, 9]. Находясь преимущественно в рассеянном состоянии, тяжелые металлы могут образовывать локальные аккумуляции в почве, где их концентрация в сотни и тысячи раз превышает среднепланетарные уровни. Следует отметить, что тяжелые металлы сравнительно быстро накапливаются в почве и крайне медленно из нее выводятся из-за высокой степени сорбции и комплексообразования с почвенными компонентами. Они способны также накапливаться в отдельных звеньях трофической цепи и, таким образом, попадать в организмы высших животных и человека, подавляя их метаболическую активность и отрицательно воздействуя на жизнедеятельность.

Известно [8], что биогенные поверхностно-активные вещества (биоПАВ, биосурфактанты), в основном производимые микроорганизмами (бактерии, грибки),

Куюкина Мария Станиславовна, д.б.н., в.н.с. лаборатории алканотрофных микроорганизмов, Пермь Ившина Ирина Борисовна, д.б.н., чл.-корр. РАН, зав. лаб. алканотрофных микроорганизмов, Пермь Костина Людмила Викторовна, аспирант Института экологии и генетики микроорганизмов, Пермь Осипенко Михаил Анатольевич, к.ф.-м.н., доцент кафедры теоретической механики, Пермь Няшин Юрий Иванович, д.т.н., профессор, заведующий кафедрой теоретической механики, Пермь способствуют десорбции солей тяжелых металлов и их удалению из почвенной среды. Данный процесс обусловлен двумя механизмами: во-первых, снижением межфазного натяжения на границе раздела фаз жидкость–твердое вещество и, во-вторых, комплексообразованием ионов металла с молекулами биосурфактанта. При этом эффективность десорбции металлов зависит от типа почвы, характера и уровня загрязнения, показателя кислотности среды, а также природы и химического строения используемого биосурфактанта. Так, показано, что внесение рамнолипидного биосурфактанта, синтезируемого бактерией Pseudomonas aeruginosa, приводит к эффективному удалению солей кадмия и никеля из загрязненной почвы [9]. Однако следует отметить, что патогенность бактерии-продуцента существенно ограничивает возможность промышленного применения рамнолипидов. В связи с этим актуально изучение металл-десорбирующих свойств биосурфактантов, продуцируемых непатогенными микроорганизмами.

В лаборатории алканотрофных микроорганизмов Института экологии и генетики микроооганизмов УрО РАН получены высокоактивные биосурфактанты, синтезируемые непатогенными актинобактериями рода Rhodococcus . Полученные биосурфактанты с высокой нефтеэмульгирующей и нефтеотмывающей способностью успешно применяются в процессах биоремедиации загрязненных почвогрунтов [2]. Лабораторные исследования показали, что Rhodococcus -биосурфактант способствует эффективной десорбции нефтяных углеводородов [6] и солей тяжелых металлов [3] из загрязненной почвы.

Для подбора эффективных приемов и создания оптимальной схемы биоремедиации необходимо построение математических моделей, адекватно описывающих процесс очистки загрязненного почвогрунта от нефти и тяжелых металлов с помощью биосурфактанта. Ранее авторами [4, 7] построена согласующаяся с экспериментальными данными модель нефтеотмывания загрязненного почвогрунта под действием Rhodococcus -биосурфактанта.

В рамках данной работы моделируются процессы фильтрации воды и биосурфактанта в почве, загрязненной солями тяжелых металлов. Предпринята попытка использовать для этой цели математическую модель, построенную для случая проникновения биосурфактанта в нефтезагрязненную почву (одномерная модель фильтрации биосурфактанта в лабораторной почвенной колонке) [4]. Путем сопоставления экспериментальных данных с результатами, полученными с помощью теоретической модели, оценивается эффективность использования биосурфактанта в технологиях очистки почвы, загрязненной тяжелыми металлами.

Описание экспериментальной части

В рамках данной работы проведены эксперименты по загрязнению модельной почвы солями тяжелых металлов (никеля и молибдена) и очистке загрязненной модельной почвы с помощью Rhodococcus -биосурфактанта. Экспериментально изучена динамика проникновения растворов солей тяжелых металлов, воды и биосурфактанта в модельной почвенной колонке.

В эксперименте использовали шесть заполненных модельной почвой стеклянных колонок (рис. 1). Здесь h 0 – высота столба налитой сверху жидкости (раствора солей тяжелых металлов, Rhodococcus -биосурфактанта или дистиллированной воды), l – глубина проникновения жидкости в почву, t – время; поверхность почвы отвечает координате x = 0.

h 0

h ( t ) 0

l ( t )

x

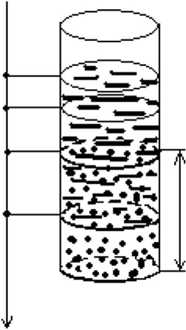
Рис. 1. Схематическое изображение модельной колонки

Параметры колонок: диаметр d и высота L слоя почвы. Значения параметров колонки: d = 28 мм, L = 410 мм. Состав модельной почвы (в объемных долях): песок – 50, глина – 30, торф – 20.

Загрязнение почвы тяжелыми металлами происходило следующим образом. В колонки сверху наливали по 50 мл водного раствора соли молибдена (NH4) 6 Mo 7 O 24 ×4H 2 O либо никеля NiSO4×7H 2 O в концентрации 40,0 мМ. После исчезновения слоя свободной жидкости над почвой в колонки вносили еще 50 мл раствора соли. При этом с начального момента времени t ₀ измеряли величину h (высота столба жидкости над почвой) и l (глубина проникновения жидкости в почву) каждые 5 мин до полного прохождения фронта жидкости через колонку (в течение 40 мин). Общее количество наливаемой в колонки жидкости было рассчитано таким образом, чтобы после полного пропитывания почвы не происходило вытекания жидкости из колонки. Результаты измерений показаны точками на рис. 2. Далее в пропитанной раствором соли почве происходил процесс сорбции металла (без дальнейшего движения жидкости) в течение 1 и 7 сут – для каждого металла. После завершения процесса сорбции почву в колонках промывали дистиллированной водой в количестве 500 мл порциями по 100 мл для удаления несорбировавшегося металла.

Для очистки почвы, загрязненной солями тяжелых металлов, применяли водную эмульсию Rhodococcus -биосурфактанта (4 г/л) (далее биосурфактант), в качестве контроля использовали дистиллированную воду. Для этого в колонки с модельной почвой, загрязненной солями никеля и молибдена в разной степени (после 1 и 7 сут сорбции), наливали биосурфактант либо дистиллированную воду объемом 500 мл, порциями по 100 мл. При этом с начального момента времени t ₀ измеряли величину h каждые 5 мин до исчезновения слоя свободной жидкости над почвой (в течение 250 мин). Результаты измерений показаны точками на рис. 3–6.

Количественное определение ионов никеля и молибдена, десорбированных из почвы в водную фазу, проводили с помощью спектрофотометра диметилглиоксимным и роданидным методом соответственно. Эффективность процесса десорбции выражали в процентах от количества сорбированного почвой металла. Полученные результаты (табл. 1) свидетельствуют о высокой эффективности применения биосурфактанта для удаления солей исследуемых тяжелых металлов из почвы. При этом интенсивность процесса десорбции молибдена и никеля из почвенной системы под действием биосурфактанта зависела от продолжительности процесса сорбции данных металлов.

Таблица 1

Экспериментальные результаты по десорбции ионов никеля и молибдена из почвы

№ п/п	Металл	Продолжительность сорбции, сут	Эффективность десорбции, %
			Rhodococcus -биосурфактант	Дистиллированная вода
1	Никель	1	76,20	1,73
2		7	60,44	1,59
3	Молибден	1	54,14	4,13
4		7	41,69	2,43

Таблица 2

Значения пористости почвы

№ п/п	Металл	Пористость почвы, α
		колонка № 1	колонка № 2	колонка № 3
1	Никель	0,35	0,38	0,34
2	Молибден	0,37	0,35	0,36

Определение пористости почвы на основании экспериментальных данных

Основными параметрами, определяющими процесс фильтрации жидкости в пористой среде, являются проницаемость K и пористость данной среды α (почвы). В настоящей работе вместо проницаемости используется более удобный коэффициент сопротивления k = n/(Kp), где П — вязкость, p — плотность. Пористость почвы вычисляется по формуле: p = ap0, где p0 - плотность чистой жидкости, p — плотность жидкости в пористой среде. По данным эксперимента можно найти значение пористости почвы а:

H ( t ) - h ( t ) ^Л                       ,

l ( t )

где H(t) = V(t)/S , V(t) - объем жидкости, находящейся в момент t в колонке, S - площадь поперечного сечения колонки. H(t) задается следующим образом:

Согласно условиям эксперимента

H ( t ) = ^

' h 0

² h 0

при t <  1 0 , при t >  t 0 .

В табл. 2 показаны найденные значения пористости почвы для колонок с модельной почвой, пропитанной раствором солей тяжелых металлов.

Из таблицы видно, что пористость почвы принимает значение от 0,34 до 0,38, в среднем а_ср = 0,36. Обнаруженная разница значений а объясняется неоднородностью почвенной смеси.

Определение коэффициента сопротивления при фильтрации РАСТВОРОВ СОЛЕЙ ТЯЖЕЛЫХ МЕТАЛЛОВ В ПОЧВЕ

В отличие от эксперимента по фильтрации биосурфактанта в нефтезагрязненной почве [4], где наблюдалась дополнительная сила сопротивления на фронте при прохождении первой порции жидкости и увеличение скорости течения при прохождении следующих порций, в данном эксперименте по фильтрации растворов солей металлов в чистой почве наблюдалось прохождение всех порций жидкости с равной скоростью. Таким образом, предполагаем, что в данной задаче жидкость течет под действием силы тяжести и объемной силы сопротивления, пропорциональной скорости. Математическая постановка задачи выглядит следующим образом [5]:

1 дp

— + g ^- kv ⁽ t ) = 0,

P 5x

^{i (} t ) = V ⁽ t ),

< l (0) = 0,                                                    (3)

pl,= l (t) =0, pl..0 = po gh (1).

Искомыми являются функция l(t) и коэффициент сопротивления k. Интегрируя первое уравнение системы (3) с учетом дополнительных условий [1], получим gh^+(g - ki) i=o. a

В данном эксперименте жидкость наливали в колонку на заданную величину h 0 и затем не доливали. В момент, когда h ( t ) = 0, жидкость снова наливали на заданную величину h 0 и после этого не доливали. Тогда для h ( t ) справедливы следующие соотношения:

h ( t ) + a i ( t ) = h ₀,

h ( t ) + a i ( t ) = 2 h ₀,

0 <  t <  1 0 , t >  t 0 .

Решая уравнение (4) с учетом (5) и начальных условий, получим аналитическую зависимость l ( t ):

l ( t ) = ^

a k

2gh^ • v2r-t0, a k

t >  1 ₀.

В данном решении неизвестным является с помощью обработки экспериментальных данных параметр k, который находится методом наименьших квадратов.

Обозначим одинаковый в обоих выражениях (6) множитель перед квадратным корнем через a; тогда i (t) = ^

0 <  t <  1 0 ,

^ a ² t ^- t ₀,

t >  t 0 ,

где

2 gh 0 a .

α k

Функцию времени в (7) обозначим через Х ( t ):

X ( t ) =

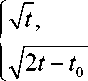
0 <  t <  1 0 , t >  t 0 .

Найдем наименьшую сумму квадратов расстояний экспериментальных точек от теоретической кривой:

N ₂

S ( a ) = I ( l_t - a X ( t_t ) ) ^ min (по a ).

i = i

Выражение для параметра a получим, находя (аналитически) минимум S( a ).

N

I WQ

= 1_____________

N

I M t i )) 2 i = 1

Преобразуем (10) с учетом (9):

a=

У Ut+У l V 2 -10

iiii 0

i = 1                 i = 5

I ti+I( 2 ti— t о)

i = 1          i = 5

Проведя численные расчеты, найдем значение параметра а и по формуле (8), с учетом ранее полученных значений пористости почвы α (см. табл. 2), определим значения коэффициента сопротивления k для почвы при фильтрации через нее растворов солей тяжелых металлов для каждой повторности эксперимента (табл. 3).

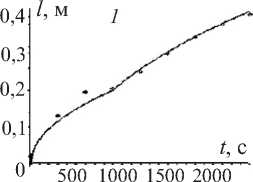
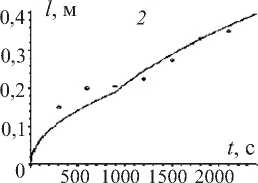
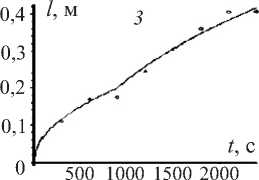
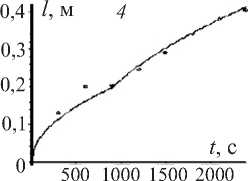
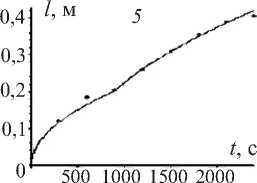
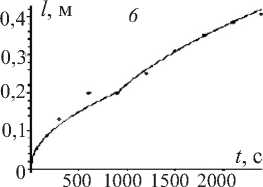
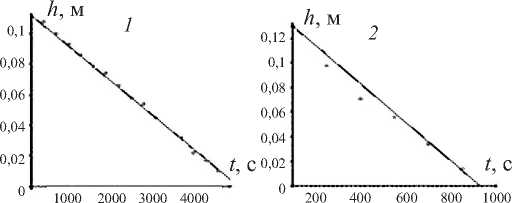
Рис. 2. Экспериментальная (точки) и теоретическая (кривая) зависимости глубины проникновения растворов солей тяжелых металлов от времени. Графики 1, 2, 3 получены для случая проникновения раствора солей никеля в почву для каждой из модельных колонок. Графики 4, 5, 6 – аналогично для случая проникновения раствора солей молибдена

Таблица 3

Значения коэффициента k при фильтрации растворов солей тяжелых металлов в почве

№ п/п	Металл	Коэффициент сопротивления k , 1/c
		колонка № 1	колонка № 2	колонка № 3
1	Никель	0,95∙105	0,96∙105	0,97∙105
2	Молибден	0,91∙105	0,92∙105	0,91∙105

На рис. 2 показаны экспериментальная (точки) и теоретическая (сплошная линия) зависимости от времени глубины проникновения растворов солей тяжелых металлов в почве. Из графиков видно хорошее соответствие экспериментальных данных и теоретических результатов, что подтверждает адекватность разработанной модели для описания процесса проникновения растворов солей тяжелых металлов в почве.

Определение коэффициента сопротивления при фильтрации РАСТВОРОВ БИОСУРФАКТАНТА И ДИСТИЛЛИРОВАННОЙ ВОДЫ В ПОЧВЕ , ЗАГРЯЗНЕННОЙ СОЛЯМИ ТЯЖЕЛЫХ МЕТАЛЛОВ

В отличие от эксперимента по загрязнению модельной почвы солями тяжелых металлов, где измеряли глубину проникновения жидкости в почвенной колонке, в данном эксперименте измеряли высоту столба жидкости (биосурфактанта или дистиллированной воды) над поверхностью почвы. Математическая постановка задачи выглядит следующим образом:

• 1    d p           , , .     _

---— + g - kv(t) - 0, p ax dh v

<

• — —a V dt ^, h (0) — h o , p . — i — 0, . p\x — o ^— P o gh(t ).

  
  

Искомой является функция h ( t ). Интегрируя первое уравнение системы (12) с учетом дополнительных условий, получим

8M ₊ g_{l +} kldh — o.                       _(l3)

a        a dt

Решая уравнение (13) с учетом начального условия, получим аналитическую зависимость h ( t ):

h ( t ) — ( h ₀ +a l ) exp ( — gt/kl ) —a l .                           (14)

В данном решении неизвестным является параметр k , который находится с помощью обработки экспериментальных данных методом наименьших квадратов.

Метод аппроксимации выбран согласно полученным экспериментальным данным: динамика проникновения биосурфактанта и воды в почву, загрязненную солями никеля, имела линейный характер, тогда как в почве, загрязненной солями молибдена, наблюдалась нелинейность данного процесса.

Значения h(t), отражающие динамику проникновения жидкости в почву, загрязненную солями никеля, аппроксимировались прямой (15), а для аппроксимации соответствующих параметров фильтрации в почве, загрязненной солями молибдена, применялась экспоненциальная функция (16):

h ( t ) = a 1 - a 2 t , где a 1 = h 0 , a 2 = g ( h 0 + a l)[kl .                    (15)

h ( t ) = a 1 exp ( - t/a 2 ) + a 3 .

Значения параметра процесса фильтрации k для каждой повторности эксперимента по десорбции никеля вычислялись тогда по формуле (17), а значения параметра процесса фильтрации k для каждой повторности эксперимента по десорбции молибдена – по формуле (18):

g ^{( h} 0 ^+a l ) ^k =----- "1— ^,

a2l k = a^lg.                                      (18)

Результаты вычислений приведены в табл. 4.

Здесь виды эксперимента: I – проникновение биосурфактанта в загрязненную солями тяжелых металлов почву после 1 сут сорбции; II – проникновение дистиллированной воды в загрязненную солями тяжелых металлов почву после 1 сут сорбции; III – проникновение биосурфактанта в загрязненную солями тяжелых металлов почву после 7 сут сорбции; IV – проникновение дистиллированной воды в загрязненную солями тяжелых металлов почву после 7 сут сорбции.

Экспериментальная и теоретическая зависимости значений h ( t ) (высота столба жидкости на поверхности почвы от времени) показаны на рис. 3–6 для соответствующих условий эксперимента.

Из графиков на рис. 3–6 видно хорошее соответствие экспериментальных данных и теоретических результатов, что подтверждает адекватность разработанной модели для описания процесса фильтрации биосурфактанта в загрязненной тяжелыми металлами почве.

Полученные результаты (см. табл. 4, рис. 3–6) свидетельствуют о высокой скорости проникновения биосурфактанта через модельную почвенную колонку, которая сопоставима, а в случае «свежего» загрязнения почвы солями тяжелых металлов превышает таковую дистиллированной воды.

Выявленная способность Rhodococcus -биосурфактанта интенсивно проникать через почвенную среду и эффективно десорбировать из нее ионы тяжелых металлов (см. табл. 1) указывает на перспективность его использования в технологиях очистки загрязненных почв и грунтов .

Таблица 4 Значения коэффициента k при фильтрации биосурфактанта и воды в почве, загрязненной солями тяжелых металлов, при различных условиях эксперимента

Параметры	Значение коэффициента сопротивления k ∙105 1/с
Металл	Никель			Молибден
№ колонки	1	2	3	4	5	6
Вид эксперимента I	1,59	1,78	1,46	0,54	0,73	0,47
II	1,73	1,47	2,64	1,88	1,96	1,14
III	2,81	1,12	3,7	1,94	2,08	1,74
IV	2,74	0,94	-	1,78	1,22	1,09
	Значение пористости почвы α
	0,35	0,38	0,34	0,37	0,35	0,36

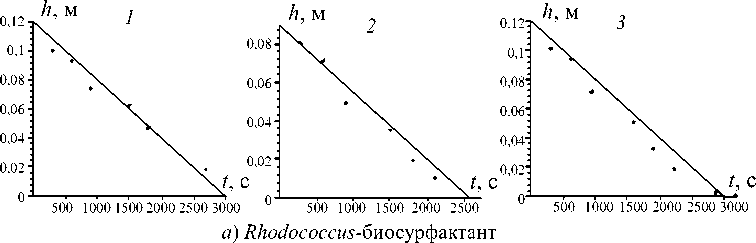
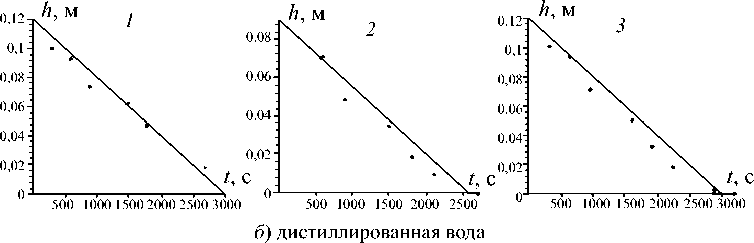
Рис. 3. Динамика проникновения биосурфактанта ( a )и дистиллированной воды ( б )в загрязненную солями никеля почву после 1 сут сорбции. Экспериментальные данные показаны точками, теоретические результаты – сплошной линией. Графики 1, 2, 3 получены для каждой из модельных колонок

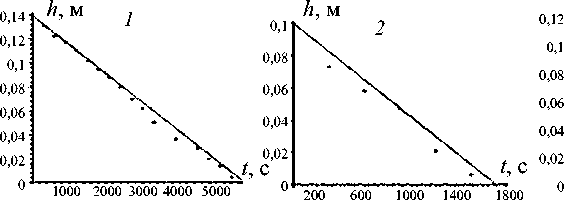
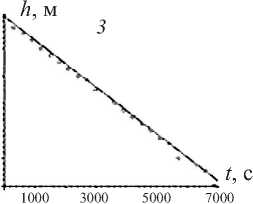
а ) Rhodococcus- биосурфактант

б ) дистиллированная вода

Рис. 4. Динамика проникновения биосурфактанта ( a )и дистиллированной воды ( б )в загрязненную солями никеля почву после 7 сут сорбции. Экспериментальные данные показаны точками, теоретические результаты – сплошной линией. Графики 1, 2, 3 получены для каждой из модельных колонок

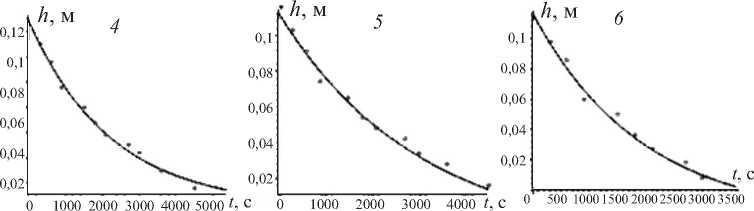
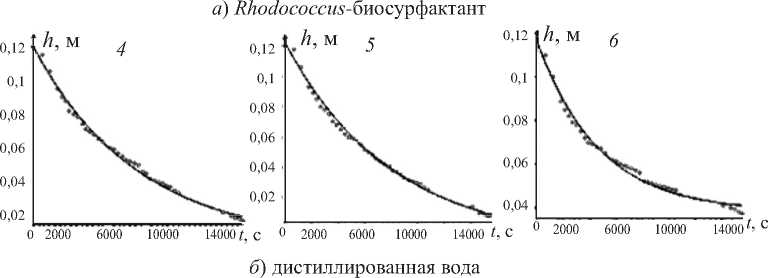
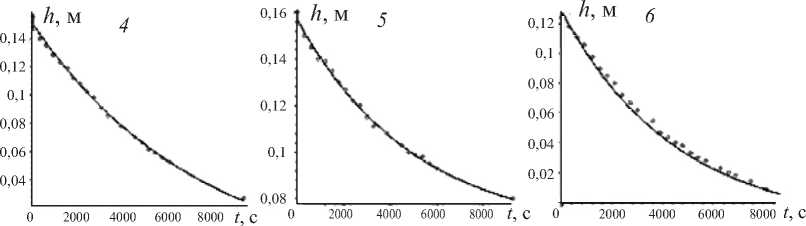
Рис. 5. Динамика проникновения биосурфактанта ( a )и дистиллированной воды ( б )в загрязненную солями молибдена почву после 1 сут сорбции. Экспериментальные данные показаны точками, теоретические результаты – сплошной линией. Графики 4, 5, 6 получены для каждой из модельных колонок

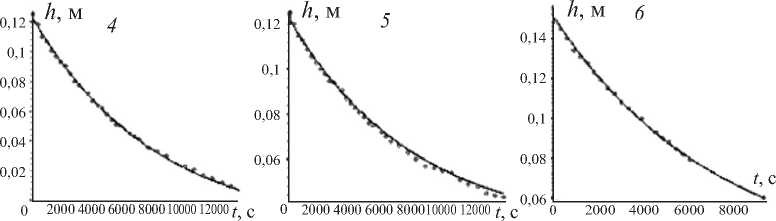
а ) Rhodococcus- биосурфактант

б ) дистиллированная вода

Рис. 6. Динамика проникновения биосурфактанта ( a )и дистиллированной воды ( б )в загрязненную солями молибдена почву после 7 сут сорбции. Экспериментальные данные показаны точками, теоретические результаты – сплошной линией. Графики 4, 5, 6 получены для каждой из модельных колонок

Заключение

В настоящей работе представлены результаты экспериментального и теоретического исследования процессов загрязнения модельной почвы солями тяжелых металлов, а также очистки загрязненной почвы с помощью Rhodococcus -биосурфактанта. Теоретически описан процесс проникновения в почву растворов солей тяжелых металлов. Построена модель фильтрации биосурфактанта в почве, загрязненной солями никеля и молибдена. На основании экспериментальных данных по динамике проникновения растворов солей тяжелых металлов, биосурфактанта и воды в модельную почвенную колонку определены константы моделирования: пористость почвы и коэффициент сопротивления. Проведенное сравнение экспериментальных данных с результатами, полученными с помощью теоретической модели, свидетельствует об адекватности разработанной модели для описания процессов фильтрации растворов солей тяжелых металлов, биосурфактанта и воды в почвенной среде.

Исследования поддержаны грантами Президента РФ для поддержки Ведущих научных школ (НШ-4112.2008.4) и Программы Президиума РАН “Молекулярная и клеточная биология”.