Моделирование процессов оценки запасов железорудного сырья в условиях неопределенности

Оценка запасов руды в настоящее время происходит на основе детерминированных моделей, различных методов усреднения и взвешивания. При этом погрешность оценки достигает 25–30%. В зарубежных странах (Япония, США) запасы железорудного сырья определяются на основе функций распределения вероятностей, операции с которыми достаточно громоздки и практические задачи решаются с применением метода Монте-Карло [1].

Наличие погрешности приборов, ошибки экспертов при проведении исследований и косвенная оценка ряда параметров приводят к необходимости использования нечетко заданных параметров. Замена нечетких параметров точечными приводит к большому количеству итерационных процедур для получения адекватных результатов.

Часто, при моделировании процессов добычи рудного сырья, параметры и коэффициенты уравнений содержат переменные с разнообразным характером неопределенности: интервальной, нечеткой, стохастической неопределенностью. В связи с чем, появляется необходимость представить всю информацию на едином формальном языке теории нечетких множеств.

Авторами предложена модель подсчета и оценки запасов железной руды различными методами в условиях неопределенности горногеологической информации, на основе теории нечетких множеств. При этом неопределенные величины намеренно интерпретируются как «нечеткие», т. к. это больше соответствует реальной промышленной ситуации, чем, если интерпретации таких величин была с точки зрения случайных.

Применение в таком случае вероятностного подхода приводит к отождествлению неопределенности со случайностью, но на практике основной природой неопределенности при подсчете запасов железной руды является именно нечеткость.

Определение запасов руды балансовым методом по промысловым данным проводится на основании уравнения, в котором выделяют величины, заданные нечетко.

Р б =

m г ^{( H}K

- h M ) -

⁽ m r - b g ) 2

( ctg « p. т. + ctg P k. в .^{) 2}

L p

где L p – длина залежи по простиранию , m г – горизонтальная мощность рудного тела, b д – ширина дна карьера; Н к – базовая глубина карьера;

h м – вертикальная мощность наносов; α р.т. – угол падения залежи; β к.в . – угол наклона борта карьера.

Согласно предлагаемому подходу каждый нечеткий параметр задается в виде соответствующей функции принадлежности µ(h), µ(α), µ(β), µ(m) .

Тогда, результирующая функция принадлежности будет иметь вид:

Ж Р б ) = max [ ^ ( h ) л ^ ( а ) л ^ ( в ) л X rn ) j   ⁽1)

где U = { ( h, а , в ,m) h, а , в ,m = р } .

Определить µ (Р б ) по (1) описанными выше аналитическими методами достаточно трудно, поэтому численные методы более эффективны в таких случаях.

Самый простой из них, обратный метод, в котором итоговая функция принадлежности определяется методом последовательного применения бинарной алгебраической операции

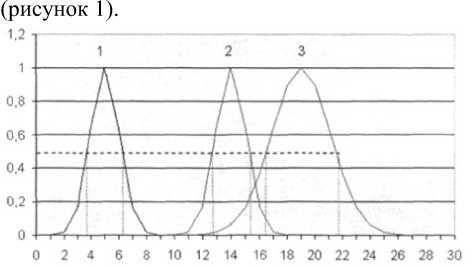
Рисунок 1. Результат численного метода сложения по дискретным уровням

Figure 1. The result is a numerical method for the addition of discrete levels

Таким образом, функция µ (Р б ) определяется на основании следующего общего алгоритма определения функции принадлежности µ(z) как результат алгебраических операций над произвольными µ(x) и µ(у) обратным численным методом:

• 1)    Для д ( x ) е [ 0, а ] , д ( у) е [ 0, в ] , а , в <  1 разбиваем отрезок [ 0, а л в ] на части точками, [ 0, а л в ] , Г е [ 0, а л в ] , i = 1, n. В данном случае а л в соответствует операции пересечения множеств.

• 2)    Каждому r i из решений уравнений µ(x) = r i и µ(у) = r i , ставятся в соответствие r i – уровневые множества:

5_r, (^x                  y

• 3)    Определяются r i итоговой функции:

• ⁵r. ( z                    ~              I ;

где: * – соответствующие интервальные операции.

Подсчет запасов железорудного сырья проводится также и на основе промышленного метода, с учетом коэффициента потерь и коэффициента разубоживания. Предлагаемая модель позволит учитывать целый ряд неточных параметров.

Рассмотрим уравнение подсчета запасов руды на основе промышленной информации:

Р = P ^{1 п}

П ^рб 1 - р

где: η и ρ – соответственно коэффициенты потерь и разубоживания.

В реальной системе точная оценка запасов руды по (2) практически невозможна, т. к. коэффициенты потерь и разубоживания определяются путем среднего взвешивания.

Таким образом, в уравнении (2) в качестве нечетких величин примем коэффициенты η и ρ.

При этом коэффициент потерь с заданной функцией принадлежности к подмножеству допустимых значений:

µ(η) = 1 -(η – а)² / b², а – b ≤ η ≤ а + b и приведенный средневзвешенный коэффициент разубоживания:

µ(ρ) = 1 - ( ρ – с)² / d², с – d ≤ ρ ≤ с + d где a, b – соответствуют максимуму функций принадлежности на интервале допустимых значений; с, d – описывают уровень разброса параметра.

Определение нечеткого значения запасов руды проведем, используя прямой аналитический метод.

1 -(η – а)² / b² = 1 – (ρ – с)² / d²

Преобразуя, согласно уравнению, получим соответственно для коэффициента потерь и коэффициента разубоживания:

ρ = £ 1 (Рп) = (ad – bc + b ρ ) / (d Рп + b ρ ),

η = £ 2 (Рп) = (ad + bc – b η ) / (d Рп – b η ).

Учитывая объединение результирующих множеств, получаем:

М ( Р п ) = 1 -

a - Р п (1 - с )  /

Р J

Р п - + b П

При отсутствии жестких границ применения моделей и наличии моделей, характеризующих технологический процесс с различных точек зрения и начальных допущениях, вполне непротиворечивым является использование теории нечетких множеств для согласования и координации моделей [2, 3].

Применимость модели можно оценить с помощью предложенной обобщенной модели агрегирования разнородной информации: решение по каждой модели m зададим в виде нечеткого множества D i на оси решений Х, тогда согласованное решение D будем представлять пересечением частных нечетких решений:

D = D 1 , ∩ D 2 ∩ ….. ∩D m

Каждому нечеткому решению D i задается функция принадлежности µ Di (x) , которая находится после проведения исследования на предмет применимости модели.

Учет фактического выполнения k – предположений о характере процесса описывает введенный показатель Li = Li1, Li2…Lik, где 0 ≤ Lij ≤ 1, причем, если предположение j о процессе для модели і идеально выполняется Lij = 1, если не выполняется Lij = 0, и 0 < Lij < 1 в остальных случаях. Тогда вид результирующей функции принадлежности:

M d ⁽ x ) = [ M d 1 ⁽ x ) ] L^{1 л} ... л [ ^ Dm ⁽ x ) ] L m

Параметры L i описывают нечеткость модели в случае нарушения условиях их существования. Данные параметры определяют с учетом дисперсии моделей, получаемой в процессе идентификации моделей для реальных процессов и объектов [4].

Невозможная объективная оценка показателя L i позволяет определять его с помощью экспертного оценивания и описывать, относительно других моделей, уровень возможности выполнения предположений, насколько точная модели и применима в конкретных ситуациях.

При отсутствии дополнительных предположений о применимости балансового и промышленного методов при подсчете запасов (т. е. L 1 = L 2 = 1), результирующую функцию принадлежности для запасов руды можно представить следующим образом:

М з ^{( Р} ) = М п ^{( Р} ) ^л М б ^{( Р} )

Решение Р0 определяется из следующего условия:

М ( Р ⁰) = max м ( Р )

Дополнительная информация о применимости методов учитывается в процессе согласования решений.

После определения системного решения µ З (Р) можно скорректировать нечеткие параметры h, α, β, m . С учетом имеющихся обозначений получаем:

у = Р, µ (у) = µ П (Р),

µ^* (у) = µ Б (Р),               (3)

µ С (у) = µ З (Р)

Выражение (3) позволяет получить согласованные нечеткие модели и агрегировать разнородную информацию по моделям.

Согласно предложенной модели также можно уточнить и нечеткие функции принадлежности ^(h), ^(а), ^(в), »(т) .

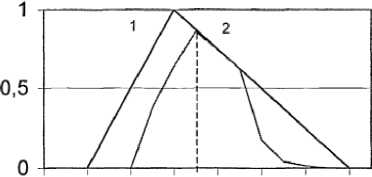
Таким образом, начальные функции принадлежности для эффективной мощности наносов, горизонтальной мощности рудного тела и т. д. уточняются, пример такого уточнения проиллюстрирован на рисунке 2, где показаны исходная ^(h) и откорректированная ^ e (h) для гипотетического месторождения по эффективной мощности наносов.

0 10 20 30 40 50 60 70 h,«

Рисунок 2. Откорректированная начальная функция принадлежности для мощности наносов

• Figure 2.    Corrected initial function supplies power sediment

Также следует отметить, что в процессе накопления горно-геологической информации при разработке рудных месторождений, уровень неопределенности для оценивания запасов руды снижается [2, 4, 5].

Особенностью разработанных моделей является возможность применения корректирующих процедур для последовательной адаптации функций принадлежности нечетких параметров.