Моделирование пульсовой волны по хаотическим рядам

В последнее время наблюдается тенденция развития медицины превентивного действия. Главной чертой методов западной медицины является то, что процесс постановки диагноза в ней происходит последовательно, а не параллельно, и поэтому требует длительного временного отрезка для обследования пациента. В связи с этим практический интерес представляет пульсовая диагностика, в частности, методы восточной медицины. Интерес к исследованию пульсовой волны вызван тем, что в ней закодирована информация о процессах, протекающих не только в сердце и кровеносной системе, но и в различных функциональных системах организма.

Большинство известных математических моделей кровотока основаны на «резервуарной» модели Отто Франка опубликованной в конце 19 века [1]. Развитие данной идеи привело к появлению ряда интересных работ [2,3], однако недостатком данных моделей является то, что эти модели являются довольно «общими» и сложно применимыми на практике.

Другой подход при моделировании кровотока заключается в использовании теории гидродинамики [4]. При использовании этого подхода возникает множество проблем: кровь сама по себе является не Ньютоновской жидкостью, течение крови происходит по сосудам и венам, нужно учитывать регуляционные функции организма и т.д. Отчасти ввиду этих причин большинство подобных моделей довольно сложны, и кроме того зачастую они применимы лишь при очень серьёзных ограничениях (например модель, описанная в работе [4] применима только для небольших участков вены).

В данной работе рассматривается способ построения динамической модели пульсовой волны по хаотическим рядам.

2.    Построение динамической модели пульсовой волны по хаотическим рядам

Коллективом авторов была создана и внедрена информационная система диагностики функционального состояния организма человека [5]. Одной из заявленных возможностей системы является работа с различными медицинскими диагностическими аппаратами, в частности с аппаратами позволяющими регистрировать сигнал пульсовой волны [6]. В ходе внедрения системы авторами была создана и наполнена база показаний данных приборов.

Сигнал пульсовой волны представляет собой замеры показаний датчиков в нескольких точках. Таким образом, показания прибора можно рассматривать как временной векторный ряд, где каждый замер является вектором состояния объекта. В работах [7,8] рассматриваются подходы и основные проблемы построения динамических моделей по временным рядам.

Искомую модель представим в виде:

dt где х - вектор состояния объекта.

Для определения функции F используем первые N значений вектора состояния. В таком случае процедура построения модели необходимо решить следующие задачи:

- по временному ряду

х(^ )

рассчитывается временной ряд

dx(tj) dt

- подбирается функция F(x,t), аппроксимирующая зависимости

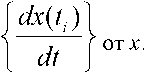
Первая задача решается путём численного дифференцирования, причём при наличии шумов необходимо использовать специальные методы.

Стандартным решением второй задачи является представление функции F в виде полинома К - той степени. Коэффициенты полинома вычисляются при помощи метода наименьших квадратов.

3.    Модель пульсовой волны

При построении модели допущены следующие упрощения:

• -    рассматриваются только первые 3 компоненты вектора х (показания датчиков с левой руки);

з

• -    функция F ищется в виде: ^, ^— | ^(Ц + А ^/) ;

  /=1

• -    для определения коэффициентов функции F рассматриваются первые 201 измерение.

Для расчёта коэффициентов искомой функции использован алгоритм основанный на нелинейной регрессии по методу наименьших квадратов с использованием метода Гаусса -Ньютона [9].

Исходный ряд представляет собой показания датчиков в точках Цои, Кан, Чаг за один сердечный цикл (рис. 1) [10]. На рисунке отчётливо видна фаза систолы (1 от 0 до 60) и фаза диастолы (1 от 60 до 200).

Наиболее удачные результаты были получены при следующем начальном приближении искомых коэффициентов: [1 1 0.5 0.5 0.5 0.5; 0.5 0.5 1 1 0.5 0.5; 0.5 0.5 0.5 0.5 1 1].

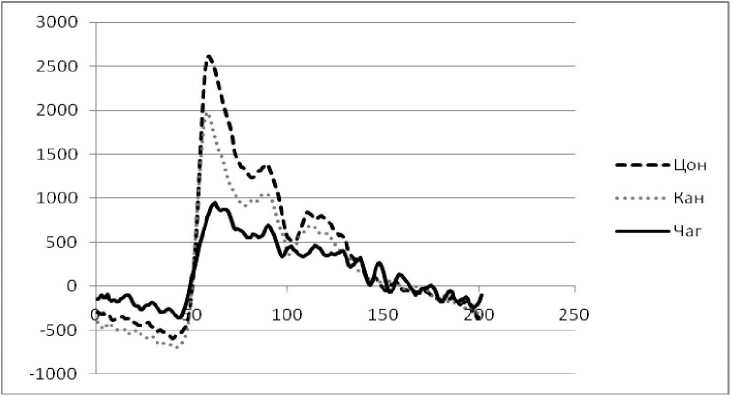
Рис. 1. Показания датчиков в точках Цон.Кан.Чаг

Значения коэффициентов полученной модели представлены в таблице 1.

Таблица 1

Значения коэффициентов модели

j	<Щ1	b[lj]	a [2J ]	b[2J]	a [3,J]	b[3J]
1	1.0000	-1.0049	1.0156	0.0028	-3.2877	0.0043
2	0.5000	-0.9969	-0.3438	-0.0009	-11.8026	0.0165
3	0.5000	-0.9934	-0.8158	0.0006	1.1124	0.0029

Полученную систему дифференциальных уравнений достаточно сложно решить аналитически, кроме того, для оценки решения нам нужны лишь значения в расчётных точках. Система была проинтегрирована при помощи метода Рунге - Кутты четвёртого порядка с начальными условиями:

х(0) = -300, у(0) = -407, z(0) = -150

Здесь х - первая координата вектора, у - вторая координата вектора, z - третья координата вектора.

Результаты численного интегрирования представлены ниже (рис. 2, рис. 3)

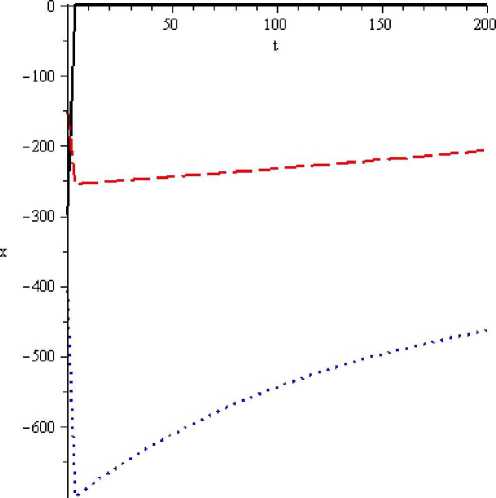
Рис. 2. Численное решение системы Сплошная линия - x(t), штрих -y(t), точки - z(t)

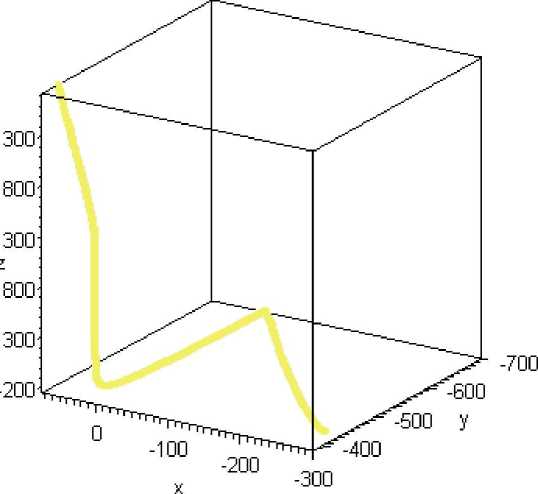
Рис.З. Фазовый портрет системы

Большинство моделей полученных в ходе численных экспериментов достаточно хорошо моделируют фазу систолы. Однако, стоит отметить, что в целом полученные модели не показывают качественных улучшений по сравнению с другими моделями [1,3,4]. Кроме того, плохо моделируется фаза диастолы и в целом модель недостаточно хорошо аппроксимируют исходные данные. Эти проблемы возникли по ряду причин:

• -    в качестве исходного ряда был использован реальный сигнал, который представляет собой замеры пульса за один сердечный цикл;

• -    вид функции F(x, t);

• -    способ нахождения производной исходного ряда.

Таким образом, необходимо решить следующие задачи:

• -    фильтрация исходного сигнала, исходный сигнал является реальным, немодельным сигналом, кроме того, нас интересуют достаточно продолжительные реализации, содержащие от 200 сердечных циклов. Таким образом, необходима фильтрация начального сигнала;

• -    нахождение вида функции F(x,t). Если моделирование фазы систолы не составляет особого труда (большинством исследователей рассматривают её как экспоненту), то моделирование фазы диастолы - достаточно сложная задача. Вполне вероятно, что функцию F(x,t) нужно брать в достаточно сложном виде, задачу подбора вида функции можно решить в частности используя аппарат нейронных сетей при наличии достаточно продолжительных реализаций исходного сигнала;

• -    нахождение производной реального сигнала. Для поиска производной подобного сигнала необходимо использовать нестандартные методы аппроксимации [8].

Заключение

Моделирования процесса кровотока и пульсовой волны в частности - сложная задача. Большинство существующих моделей математически сложны и неудобны для применения на практике. В тоже время исследования подобных моделей важны для практики.

В работе рассматривается подход, к моделированию пульсовой волны основанный на методе реконструкции обыкновенных дифференциальных уравнений по хаотическим рядам. Приведены результаты тестирования подхода на реальных данных, рассмотрены основные проблемы и способы их решения.