Моделирование рабочего пространства планарного трёхзвенного манипулятора
Автор: Шевелева Т.А., Ляшков А.А.
Журнал: Онтология проектирования @ontology-of-designing
Рубрика: Прикладные онтологии проектирования
Статья в выпуске: 1 (51) т.14, 2024 года.
Бесплатный доступ
Проведено исследование рабочего пространства планарного трёхзвенного манипулятора. За основу взяты аналитические зависимости, позволяющие решить прямую задачу кинематики, т.е. определить координаты центра схвата по трём обобщённым координатам манипулятора. Выполненный анализ позволил дать геометрическую трактовку зависимостей. Установлено, что рабочим пространством манипулятора является трёхпараметрическое множество точек. На плоскости это множество точек представлено в виде двух дисков, состоящих из кольцевых ячеек, для которых получены соответствующие аналитические зависимости. Геометрическим образом этого множества является трёхмерный тор. Полученные модели визуализированы, что облегчает решение указанной задачи. Для определения значений обобщённых координат центра схвата в зависимости от его положения выполнено отображение ортогональным проецированием полученных в работе семейств окружностей в четырёхмерное пространство. В результате получены трёхмерные гиперповерхности в четырёхмерном пространстве. Их исследование предложено выполнять построением моделей сечений гиперповерхностей гиперплоскостями. Такие модели в режиме визуализации позволяют решать прямую и обратную задачи кинематики исследуемого манипулятора.
Геометрическое моделирование, манипулятор, рабочее пространство, гиперповерхность, визуализация
Короткий адрес: https://sciup.org/170203865
IDR: 170203865 | УДК: 004.9:621.9.07:621.833 | DOI: 10.18287/2223-9537-2024-14-1-71-81
Текст научной статьи Моделирование рабочего пространства планарного трёхзвенного манипулятора
Планарные двух- и трёхзвенные манипуляторы (ТМ) часто используются в робототехнике, в частности, в качестве испытательных стендов при исследовании ТМ [1]. Одна из задач исследования заключается в генерации желаемых траекторий ТМ. В статье [2] такая задача для планарного ТМ рассматривается на основе решения обратной задачи кинематики с помощью нейронной сети. Сложность решения обратной задачи кинематики для роботов-манипуляторов обусловлена геометрией робота и нелинейными тригонометрическими уравнениями, описывающими положение его звеньев в декартовом пространстве [3, 4].
Ряд способов решения этой задачи приводится в работах [5-7]. Суть метода обратных преобразований заключается в составлении матриц перехода из системы координат одного звена в систему координат соседнего звена. В этом случае используют метод Данавита– Хартенберга. Известны методы решения обратной задачи кинематики с использованием матриц Якоби [8]. Эффективность геометрического и компьютерного моделирования для визуализации объектов показана в работе [9].
Важной задачей является установление рабочего пространства манипулятора [10]. Основными методами исследования рабочего пространства являются: аналитический, численный, геометро-графический, в т.ч. с использованием систем автоматизированного проектирования и компьютерной графики.
В работе [11] выполнен систематический анализ характеристик рабочего пространства на основе исследования соотношений между длинами звеньев манипулятора и выделены три класса ТМ. Модели решений представлены в виде дисков, включающих диапазон кольцевых рабочих ячеек. Областями этих диапазонов являются облака точек.
В статье [12] для моделирования рабочего пространства ТМ использован численный метод Монте-Карло для решения прямой задачи кинематики.
В работе [13] исследование направлено на определение положения и ориентации базы манипулятора относительно заранее заданной рабочей среды. Численные методы размещения робота основаны на определении точной границы рабочего пространства. Задача решается без применения алгоритма обратной кинематики с использованием некоторой «меры ловкости». Предложенный численный метод размещения роботов-манипуляторов основан на максимизации ловкости в заданных целевых точках. В качестве примера рассмотрен плоский манипулятор с тремя степенями свободы.
В статье [14] представлено алгебраическое решение задачи по установлению граничного рабочего пространства 3D-манипулятора в декартовом пространстве. Показано, что граничная кривая поперечного сечения может быть описана полиномом 16-го порядка. Исследованы геометрические особенности этой кривой.
Практический интерес представляет обнаружение возможных пустот в рабочей области, так как это область недостижимых точек для схвата манипулятора. Наличие бугров и пустот можно обнаружить по анализу геометрических особенностей граничных поверхностей и кривых. Эффективным инструментом для достижения этих целей является разработка соответствующих геометрических моделей и компьютерных технологий.
Актуальными являются исследования, направленные на развитие методов геометрического и компьютерного моделирования рабочего пространства рычажных механизмов применительно к их использованию в среде интегрированных систем компьютерной графики.
Целью настоящей работы является исследование рабочего пространства планарных ТМ средствами геометрического и компьютерного моделирования.
1 Теоретические основы 1.1 Геометрические модели рабочего пространства планарного ТМ на плоскости
Планарные ТМ - это кинематические механизмы с тремя обобщёнными координатами. Как и двухзвенные, они функционируют подобно человеческим рукам. Результаты их анализа позволяют исследовать более сложные движения, когда манипуляторы имеют число независимых параметров более двух.
Кинематическая (расчётная) схема планарного ТМ показаны на рисунке 1. Заданы длины звеньев 11, 12 и 13, а также углы поворота звеньев u, v и w (обобщённые координаты).
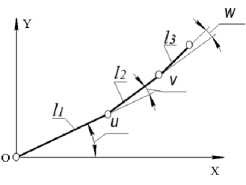
Рисунок 1 - Расчётная схема планарного трёхзвенного манипулятора
Зависимости, связывающие координаты центра схвата с обобщёнными координатами манипулятора, определяются системой уравнений:
х = x(u, v, w ) = I ! • с о su + I 2 • с ss(u + v) + Z з • с о s(u + v + w), у = y(u, v, w ) = I ! • s iuu + 1 2 • siu(u + v) + l з • siu(u + v + w) (1)
Эти уравнения определяют трёхпараметрическое множество точек (облако) на плоскости. Они позволяют решать прямую задачу кинематики аналитическим методом. В настоящей работе пред- лагается геометрическое представление этих уравнений и множества точек, описываемых этими уравнениями.
Преобразуя систему уравнений (1) к виду
X - I! • С О S и = 12 • С О s(u + v) + Z з • с о s(u + v + w), у — I! • s iuu = 12 • sin(u + v) + Zз • sin(u + v + w), (2)
можно получить
(x — Z ! • с о s u)2 + (y — Z ! • s i nu)2 = Z2 + 1 2 +2 • Z 2 • Z з • с о sw. (3)
Уравнение (3) определяет семейство эксцентрических окружностей с координатами цен-трое x0 = Z ! • с о su, y0 = Z ! • s iuu.
Множество этих точек задаёт окружность радиусом R 0 = Zг . Она является линией центров окружностей радиусами
R i = 7а 2 ) 2 + 0 з ) 2+2(Z 2 )(Z з )cosw. (4)
При этом радиусы окружностей изменяются в диапазоне
I 2 — Z з < ^ < Z 2 + Z 3 . (5)
График этой функции представлен на рисунке 2 для длин звеньев механизма:
Z г = 15, Z 2 = 7,Z 3 = 4.
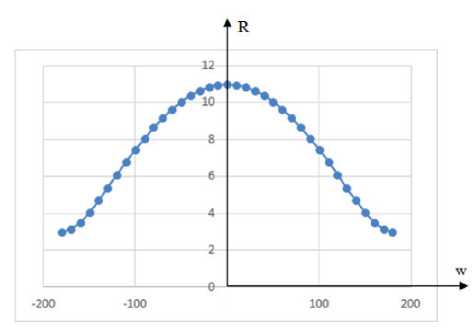
Рисунок 2 - Зависимость радиуса эксцентрических окружностей от параметра w (в градусах) Примеры семейств эксцентрических окружностей приведены на рисунке 3.
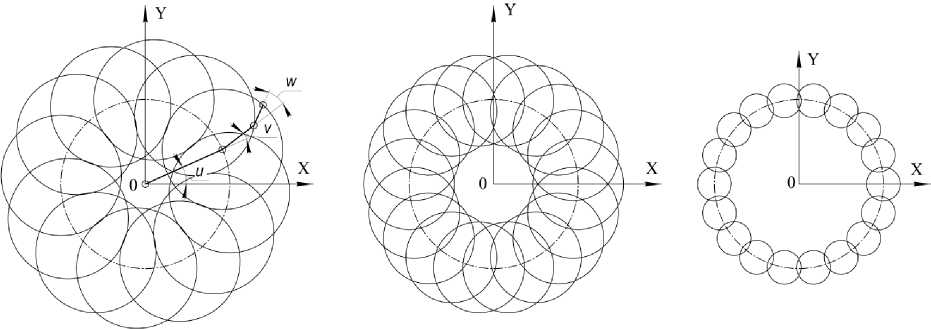
а) б) в)
Рисунок 3 – Семейства эксцентрических окружностей для различных значений параметра w : а) w =0°, б) w =90°, в) w =180°
Следующее преобразование уравнений системы (1) приводит к уравнению (6):
%2 + у2 = I 22 + 1 22 + 1 32 + 2 • I г ■ I 2 • с о sv + 2 • I г ■ I з • с о s(v + w) + 2 • 1 2 • 1 3 • с о sw. (6) Это уравнение определяет двухпараметрическое семейство концентрических окружностей с центром в начале системы координат и радиусами
R i = ^ I2 2 + I 2 2 + I з 2 +2 ■ Z • ■ 1 2 ■ с о sv + 2 ■ Z • ■ I з ■ с о s(v + w) + 2 ■ Z 2 ■ Z з " ^ о sw. (7)
График функции (7) представлен на рисунке 4.
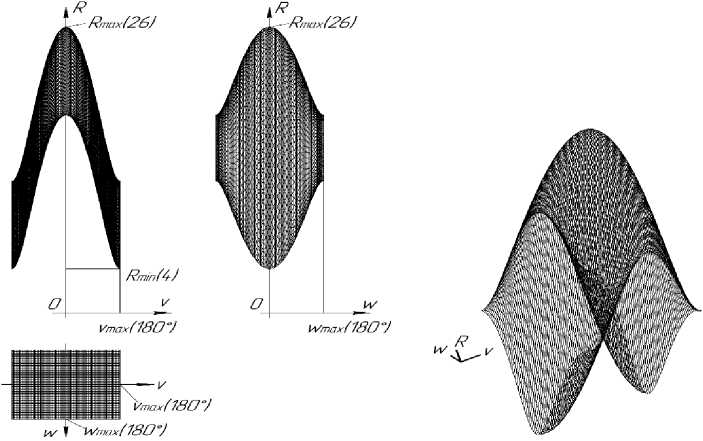
Рисунок 4 - График функции R = f ( v , w ), -180°< v <180°, -180°< w < 180°
Примеры семейств концентрических окружностей приведены на рисунках 5 и 6.
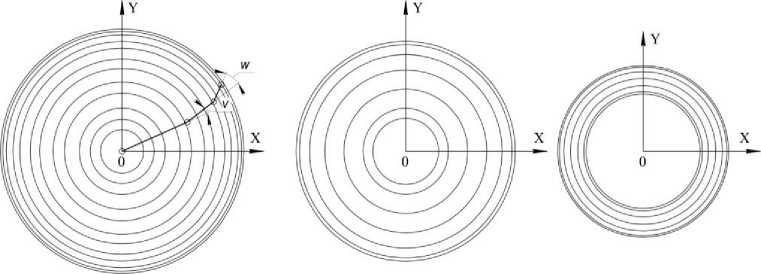
а) б) в)
Рисунок 5 - Семейства концентрических окружностей для различных значений параметра w : а) w =0°, б) w =90°, в) w =180°
На основании полученных результатов можно сделать следующие выводы:
-
■ рабочим пространством ТМ является трёхпараметрическое множество точек. На плоскости это множество точек («облако») можно представить в виде двух дисков, включающих диапазон кольцевых рабочих ячеек. На одном диске этот диапазон состоит из двухпараметрического семейства эксцентрических окружностей, а на другом - двухпараметрическое семейство концентрических окружностей;
-
■ геометрическим образом двух множеств является трёхмерный тор [15], являющийся моделью конфигурационного пространства рассматриваемого манипулятора;
-
■ так как данный манипулятор стационарный, то его рабочее пространство совпадает с конфигурационным пространством с учётом возможных ограничений на диапазоны изменения обобщённых координат;
-
■ полученные результаты обобщают известные [1, 10, 16], но имея геометрическую
направленность исследования, предоставляют возможность более широкой трактовки понятия двух дисков, а также обладают большей наглядностью.
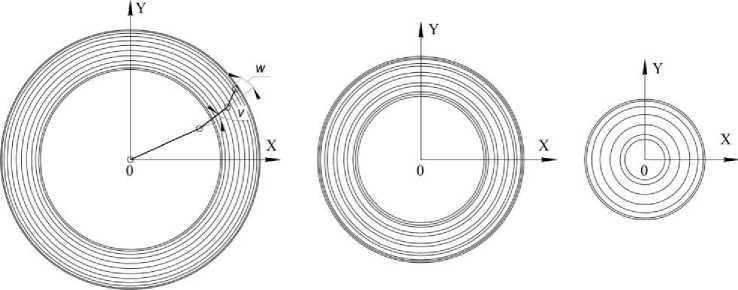
а) б) в)
Рисунок 6 – Семейства концентрических окружностей для различных значений параметра v : а) v =0°, б) v =90°, в) v =180°
-
1.2 Геометрические модели рабочего пространства планарного ТМ
в четырёхмерном пространстве
Полученные результаты определяют рабочее пространство манипулятора и его границы в плоскости механизма, т.е. в системе координат XY . Однако такие модели, решая прямую задачу кинематики, не позволяют определять значения обобщённых координат по заданному положению точки схвата, т.е. решать обратную задачу. Ниже предлагается новая трактовка системы уравнений (1) с учётом семейств окружностей, описанных в разделе 1.1.
Для каждого фиксированного значения u предлагается рассматривать семейства окружностей на плоскости (рисунок 3) как проекции окружностей некоторого многообразия из четырёхмерного пространства [17, 18]. Пусть каждая из окружностей этого семейства смещена параллельно гиперплоскости XY на величину, пропорциональную параметрам v и u . Тогда семейство таких окружностей записывается уравнениями:
X = (Qu, V, W) = I1 • С О SU + I2 • С os(u + v) + I з • с о s(u + v + w), у = y(u, v, w) = I1 • s iuu + 12 • siu(u + v) + Zз • siu(u + v + w), (8)
z = P1 • V, t = P2 • u, где Р1 и Р2 – некоторые константы.
Эта система уравнений описывает трёхмерную гиперповерхность в четырёхмерном пространстве. Одним из вариантов исследования такой поверхности может быть получение её сечений гиперплоскостями. В качестве примера на рисунке 7 приведены каркасные модели двумерных V -поверхностей, полученных в сечении гиперповерхности (8) гиперплоскостями t i . Семейства этих поверхностей являются циклическими винтовыми поверхностями.
Выполнив аналогичное отображение в четырёхмерное пространство семейства концентрических окружностей, показанных на рисунке 5, но пропорционально параметрам w и u , можно получить уравнения:
X = x(u, V, w) = Z1 • с о uu + 12 • с о s(u + v) + Z з • с о s(u + V + w), у = y(u, v, w) = Z1 • siuu + 12 • si n(u + v) + Zз • si n(u + v + w), z = P1 • w, t = P2 • u, (9)
где Р 1 и Р 2 - некоторые константы.
Эта система уравнений описывает ещё одну трёхмерную гиперповерхность в четырёхмерном пространстве. Сечениями этой гиперповерхности гиперплоскостями t i являются циклические поверхности с прямолинейными направляющими. На рисунке 8 приведены каркасные модели таких W -поверхностей.
Поверхностные модели (рисунки 9 и 10), получены на основе каркасных моделей сечений гиперповерхностей. Они предоставляют возможность в режиме визуализации решать как прямую, так и обратную задачи кинематики ТМ.
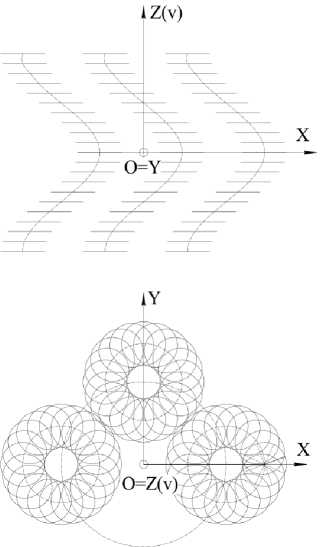
Рисунок 7 - Каркасные модели V-поверхностей для u =0°, 90°, 180°
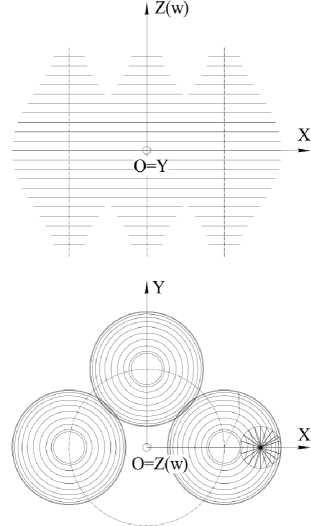
Рисунок 8 - Каркасные модели W-поверхностей для u =0°, 90°, 180
Таким образом, полученные системы уравнений (8) и (9) задают гиперповерхности, определяющие рабочее пространство ТМ. Для его исследования получены трёхмерные геометрические и компьютерные модели сечений гиперповерхностей. В отличие от двумерных моделей полученные поверхности в наглядном виде с необходимой точностью устанавливают связь «облаков» точек рабочего пространства с обобщёнными координатами. Получен- ные поверхности позволяют моделировать и находить оптимальные траектории перемеще- ния схвата манипулятора.
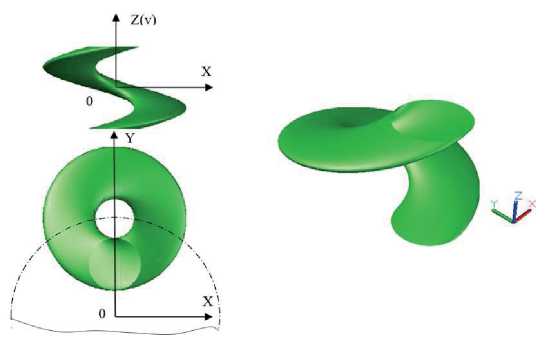
Рисунок 9 - Поверхностная модель V -поверхности для u =90°
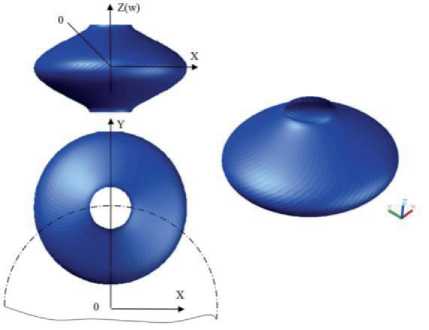
Рисунок 10 - Поверхностная модель
W -поверхности для u =90°
2 Результаты компьютерных экспериментов
Проведённые исследования трёхпараметрических семейств точек на плоскости, являющихся рабочим пространством планарного ТМ, позволили получить четырёхмерные анали- тические и компьютерные модели этого пространства. Компьютерные модели позволяют использовать их для решения как прямой, так и обратной задачи кинематики рассматриваемого механизма. Для подтверждения полученных выводов по разработанным алгоритмам и программам выполнен ряд компьютерных экспериментов. При этом учитывалось, что в промышленных манипуляторах обобщённые координаты изменяются в определённых диапазонах. Ниже приведены результаты двух экспериментов.
На рисунке 11 показана 3D -модель
V
-поверхности и совмещённая с ней модель фрагмента рабочего пространства для следующих значений параметров:
l
1
=15, 1
2
=7, 1
з
= 4, -120°
Рисунок 12 иллюстрирует 3D-модель
W
-поверхности и совмещённую с ней модель фрагмента рабочего пространства для следующих значений параметров:
l
1
=15, l
2
=7, l
3
=4, -120°
Значения обобщённых координат дают решение обратной задачи кинематики исследуемого манипулятора.
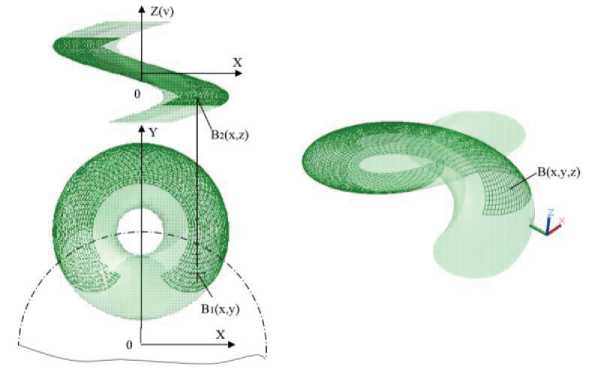
Рисунок 11 - Модель V -поверхности и совмещённая с ней модель фрагмента рабочего пространства
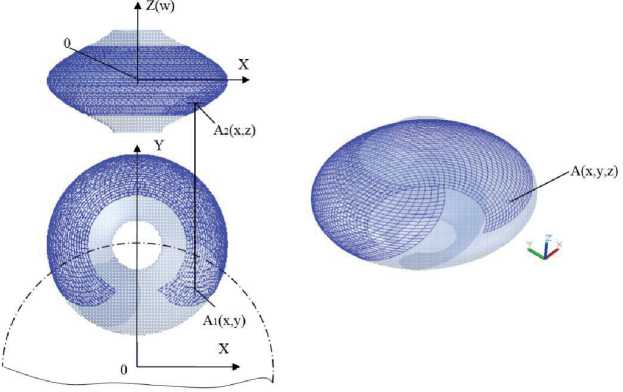
Рисунок 12 – Модель W -поверхности и совмещённая с ней модель фрагмента рабочего пространства
Заключение
Выполненная геометрическая трактовка аналитических зависимостей, определяющих трёхпараметрическое семейство точек (облако), задающих рабочее пространство планарного ТМ, позволила получить ряд новых результатов.
На плоскости это множество точек представляет собой два диска, содержащих диапазоны кольцевых рабочих ячеек, состоящих из двухпараметрических семейств эксцентрических и концентрических окружностей. Геометрическим образом этих семейств является трёхмерный тор. Отображением полученных семейств окружностей в четырёхмерное пространство получены два вида гиперповерхностей, являющихся геометрической моделью рабочего пространства манипулятора. Получены сечения этих гиперповерхностей гиперплоскостями. Модели гиперповерхностей и их сечений позволяют решать прямую и обратную задачу кинематики планарного ТМ.
Предметом дальнейших исследований может быть определение границ рабочего пространства ТМ на основе установления дискриминантов полученных поверхностей на гиперплоскостях. Анализ предложенных моделей позволит выявить возможные «мёртвые» зоны рабочего пространства и особенные элементы на его границах.
Список литературы Моделирование рабочего пространства планарного трёхзвенного манипулятора
- Зенкевич С.Л., Ющенко А.С. Основы управления манипуляционными роботами. М.: Изд-во МГТУ. 2004. 478 с.
- Duka A. V. Neural network based inverse kinematics solution for trajectory tracking of a robotic arm. The 7th International Conference Interdisciplinarity in Engineering (INTER-ENG 2013) Procedia Technology. 12 (2014). P.20-27. DOI: 10.1016/j.protcy.2013.12.451.
- Aristidou A., Lasenby J. Inverse Kinematics: a review of existing techniques and introduction of a new fast iterative solver. Technical Report. CUED/F-INFENG/TR-632. University of Cambridge. 2009. 74 p. DOI: 10.1007/978-0-85729-811-9_3.
- Angeles J. Fundamentals of Robotic Mechanical Systems. Theory, Methods and Algorithms. 3 -rd ed. Springer. 2007. 550 p.
- Whitney D. E. The mathematics of coordinated control of prosthetic Arms and Manipulators. Engineering, Mathematics, Medicine Journal of Dynamic Systems Measurement and Control-transactions of The ASME. 1972. Vol. 94. no. 4. P.19-27. DOI: 10.1115/1.3426611.
- Denavit J., Hartenberg R S. Cinematic notation for Lower-Pair Mechanisms Based on Matrices. J. Appl. Mech. 1955. Vol.77. P. 215-221.
- Шамраев А.Д. Обзор методов решения обратной задачи кинематики для манипуляторов. Фундаментальные основы инновационного развития науки и образования: сб. ст. VI Междунар. науч.-практич. конф. В 3 ч. Ч. 1. Пенза: МЦНС «Наука и просвещение». 2019. С.51-53.
- Pechev A.N. Inverse Kinematics without matrix inversion. Proc. 2008 IEEE International Conference on Robotics and Automation (ICRA 2008), 19-23 May, 2008. Pasadena, 2008. P.2005-2012. DOI: 10.1109/R0B0T.2008.4543501.
- Денисова Е.В., Гурьева Ю.А. Аналитическое и компьютерное моделирование поверхностей методом криволинейного проецирования // Онтология проектирования. 2023. Т.13. №2(48). С.204-216. DOI:10.18287/2223-9537-2023-13-2-204-216.
- Zar T., Lin P.W., Win S.Y. Workspace Analysis of Two-link Planar Manipulator. International Journal of Science and Engineering Applications. 2019. Volume 8. Issue 08, P.380-383. DOI: 10.7753/IJSEA0808.1028.
- Guo W.Z., Gao F., Mekid S. A new analysis of workspace performances and orientation capability for 3 -dof planar manipulators. International Journal of Robotics and Automation, 2010. Vol. 25, No.2, P.89-101. DOI: 10.2316/Journal.206.2010.2.206-3326.
- Zhu J., Tian F. Kinematics Analysis and Workspace Calculation of a 3-DOF Manipulator. 2nd International Symposium on Resource Exploration and Environmental Science 2018 IOP Conf. Ser.: Earth Environ. Sci. 170 042166. P.1-9. DOI:10.1088/1755-1315/170/4/042166.
- Abdel-Malek K., Yu W. Placement of Robot Manipulators to Maximize Dexterity. International Journal of Robotics and Automation. 2004. DOI: 10.2316/Journal.206.2004.1.206-2029.
- Ottaviano E., Husty M., Ceccarelli M. Identification of the Workspace Boundary Of a General 3-R Manipulator. Journal of Mechanical Design. January 2006. 128(1). DOI: 10.1115/1.2120807.
- Тёрстон У.П., Уикс Д.Р. Математика трехмерных многообразий. В мире науки. Scientific American. М.: Изд-во «МИР», №9. Сентябрь. 1984. С.76-90.
- Serweryouns S., Hasan D.S. Kinematic Workspace Modelling of Two Links Robotic Manipulator. Anbar Journal Of Engineering Science. 2020. Vol. 4. P.101-106. DOI: 10.37649/aengs.2020.171281.
- Thom R Sur la theorie des envelopes. J. de math. pur et appl. 1962. Vol. 41, № 2. Р.177-192.
- Lyashkov A.A., Sheveleva T.A. Geometric modeling in the problems of lever mechanism kinematics research. Journal of Physics: Conference Series. 14. "XIV International Scientific and Technical Conference "Applied Mechanics and Systems Dynamics". AMSD 2020" 2021. P.012053. DOI: 10.1088/1742-6596/1791/1/012053.


