Моделирование рабочего пространства станка с параллельной кинематикой

Введение. Быстрое развитие современного машиностроения требует создания высокоэффективного технологического оборудования, способного обрабатывать сложные поверхности с высокой точностью, за один установ, без применения ручного труда. Проектирование оборудования является сложной системной задачей, при решении которой необходимо учитывать такие параметры как металлоемкость, габаритные размеры, точность, объем и форма рабочего пространства и др. В настоящее время технологическое оборудование для механической обработки сложных поверхностей строится, как правило, с использованием принципов последовательной кинематики. Однако станки, обладающие высокой жесткостью конструкции и высокой точностью, предпочтительнее строить с использованием параллельных кинематических цепей, нежели последовательных. Большое ускорение рабочего органа станка достигается за счёт перемещения незначительных масс, а замкнутая кинематическая цепь обеспечивает более высокую жесткость всей конструкции. Станки, построенные на основе параллельной кинематики, могут представлять собой достаточно жёсткую пространственную ферму (при заторможенных приводах), а малое число соединений на пути замыкания сил приводит к меньшим деформациям и более высокой точности воспроизведения движения [5].

В отличие от технологического оборудования традиционной компоновки, рабочее пространство которого представляет собой простые трехмерные тела, ограниченные плоскостями, цилиндрическими и сферическими поверхностями, форма рабочего пространства технологических машин с параллельными приводами представляет собой сложную объемную фигуру. И только исследование станка с параллельной кинематикой путём создания его математической модели может дать ответ проектировщику о размерах и форме рабочего пространства.

При расчете рабочего пространства необходимо учитывать ограничения обобщенных координат, значений углов наклона шарниров, возможные коллизии, а также наличие особых положений.

Исследуемый объект. Математическая модель станка была построена на основе механизма, представленного на рис. 1. Механизм состоит из двух подвижных платформ 1 и 2, жестко соединенных между собой трубой 3. Платформы связаны с неподвижным основанием 4 штангами 5 переменной длины L_t (z = 1... б). Двухстепенные шарниры основания A, (z -1... б) расположены на окружности радиусом Rq , а сферические шарниры платформ В, (/ = 1... б) - на окружности радиусом К_П.

Шарниры верхней и нижней платформы смещены друг относительно друга на 60°. Особенностью конструкции механизма является то, что в исходном положении (при равных длинах

Сулацкая Е.Ю., Петрова Л.Н.

штанг Д) проекции штанг на плоскость СXV касательны к окружности расположения центров сферических шарниров.

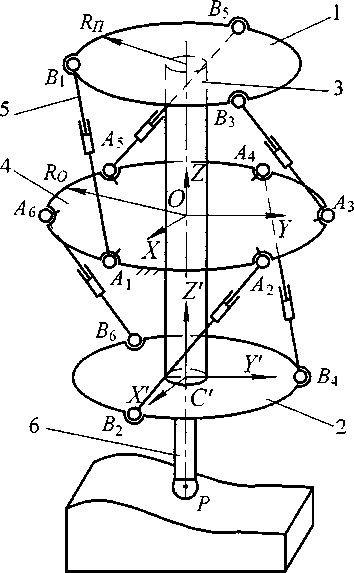
Рис. 1

Для определения числа степеней свободы W механизмов с параллельной кинематикой может быть использована формула Сомова-Малышева [1]:

W = 6п-5р₅-4р₄-Зр₃-2р₂- р_х, где п - количество подвижных звеньев кинематической цепи, р, - количество кинематических пар /-го класса. Применительно к данному механизму и = 13 - число подвижных звеньев, р₃ = 6 - число трехстепенных сферических шарниров, р^ = 6 - число двухстепенных кардановых шарниров, р₅ = 6 - число поступательных пар:

^ = 6-13-5-6-4-6-3-6 = 6.

Следовательно, механизм относится к классу «гексаподов».

Создание математической модели механизма с параллельной кинематикой сводится к описанию движения выходного звена механизма в зависимости от его обобщенных координат. Обобщенными координатами принято называть независимые между собой параметры любой размерности, число которых равно числу степеней свободы механизма, однозначно определяющие положение его выходного звена [1].

В качестве выходного звена принимается узел, состоящий из двух жестко соединённых подвижных плат форм, на котором крепиться обрабатывающий инструмент 6 (см. рис. 1).

Для математического моделирования станка-гексапода, выходное звено которого перемещается посредством штанг переменной длины, в качестве обобщенных координат удобно использовать L -координаты [2]. В системе L -координат положение твердого тела в пространстве определяется с помощью шести положительных чисел Д (/ = 1...б), равных длинам отрезков, соеди няющих точки тела с точками неподвижной базы таким образом, что при заданном значении Д образуется геометрически неизменяемая структура.

Введем неподвижную систему координат (СК) OXYZ , связанную с основанием, и подвижную СК CXYZ*, связанную с подвижной платформой. Точка С' - характерная точка подвижной платформы; в качестве характерной может выступать точка связанного с подвижной платформой инструмента; (x_r ,у_с,z_c.) - координаты точки С' в СК OXYZ. Тогда задача моделирования сводится к нахождению Д (/ = 1...б) по известным координатам точки С' и направляющим косинусам I ,т ,п_р (у = 1,2,3) осей СК CXYZ' относительно СК OXYZ.

В общем виде величина Д определяется через координаты соответствующих шарниров в некоторой СК:

= (^ха, -^хв)²*(Уа, ~Ув)²+(^г_А. -^zb)², где / = 1..,6.                                 (1)

Примем, что в (1) используются координаты шарниров в неподвижной СК. Из конструкции механизма известны координаты сферических шарниров в подвижной СК. Их пересчет в неподвижную СК можно выполнить следующим образом:

XBj = ЦХ'в, *ky Bj +hZ Bi + xc',

Ув, = mpc'_B. + m₂y'_B. + m₃z'_B. + y_c;                                                           (2)

zBi = п\х) ^У'в, +n3z'Bi +zc.

Расчет и конструирование

Направляющие косинусы I ,тп ,п ,^j = \, 2,3) можно определить с использованием, напри мер, углов Крылова у , и, у [4]:

к к Ч CyCyA-SuSySy SyCu -Су Sy + Sy SuCy тх т2 т2 = -SyCyA-SuCySy CyCu Sy Sy + Cy SuCy >                          (3) пх и2 и3 CuSy      -Su      CuCy где для сокращения записи введены обозначения: Су = cosy/, Sy = sin у и т. д.

Механизм промоделирован со следующими параметрами: R_n = 56 мм, Rq = 300 мм.

Моделирование рабочего пространства выполнялись при следующих ограничениях: минимальные длины всех штанг L_MIN = 335 мм, максимальные длины всех штанг L^^ = 485 мм.

Положение механизма, при котором все штанги имеют равную длину и у = 0°, и = 0°, у = 0°, считаем исходным.

Расчет рабочего пространства проводился численным методом с использованием соотношений (1)—(3) и в соответствии со следующим алгоритмом:

Шаг 1. Ввод исходных данных, задающих кинематику механизма и положение характерной точки, для которой далее будет рассчитываться рабочее пространство.

Шаг 2. Определение области допустимых значений координат характерной точки.

Шаг 3. Расчет L -координат механизма для каждой точки области допустимых значений.

Шаг 4. Анализ возможности данного положения, сделанный по ограничениям длин штанг.

Шаг 5. Формирование области возможных положений механизма.

Данный расчет повторяется до тех пор, пока не будут перебраны с некоторым шагом все возможные координаты выходного звена, принадлежащие области допустимых значений. В данном методе точность расчета рабочего пространства зависит от шага дискретизации во втором блоке.

На рис. 2 представлено рабочее пространство, построенное при условии, что углы поворота подвижной платформы у, и, у равны нулю.

Исходя из опыта, можно предположить, что положение, показанное на рис. 3, является особым. Оно достигается при повороте подвижной платформы на такой угол у , при котором угловые координаты шарниров подвижной платформы становятся равными угловым координатам соответствующих шарниров основания, а прямые, проведенные вдоль раздвижных штанг Д Д пересекают ось ОС', где С - центр окружности, на которой лежат центры сферических шарниров.

Известно, что критерием особых положений является равенство нулю Якобиана J механизма [3].

az, ЭЦ ец 8LX 8Ц 8xP 9yP 8zP 8y 8u dy 8L2 8L2 8L2 8L2 8L2 8xP дуР 8zP 8y du dy 8L6 8L6 3L6 3L6 3L6 8L6 8xP Зур 8zP 8y du dy где L, =f(xP,yP,zP,y,u,y),i = 1...6.

Подставив выражения (2) и (3) в формулы (1) и сделав некоторые преобразования, получим: А ² - ^Х В, ⁺^ В/ ^+Z В; ⁺(^ХС ^{- Х}А₍ )^{2 +} (Ус ^- УAj )^{2 +} (²С ~ ² А, )^{2 +}

+ 2

+ 2

+ 2-

(Су/ Cy + Sy Su Sy)-x'_B.+Sy/Cu-y'_B.+(Sy/SuC/-Cy/S/)- z’_B. (С у S и Sy - S у Cy\ x’_B. +CyCu- y’_B. +(S у Sy + С у S и Су) • z’_B. CuSy- х'_в. -Sи • у'_В/ А-СиСу ■ z'_B ]• (z_c. - z_k,), i = 1 ...6.

Сулацкая Е.Ю., Петрова Л.Н.                   Моделирование рабочего пространства станка___________________________________________________________с параллельной кинематикой

Выражения (5) ставят в соответствие шесть обобщенных координат L_t (/ = 1. ..б) и шесть ко-

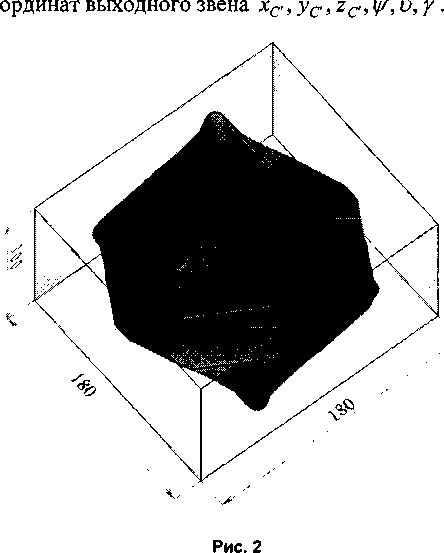
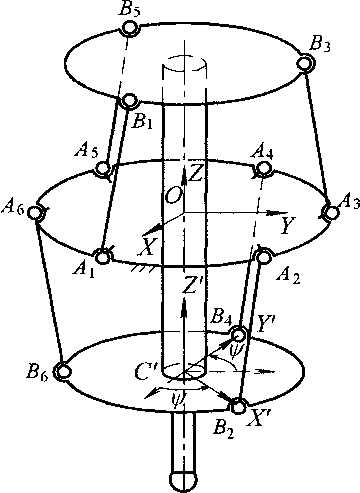
Рис. 3

Расчет Якобиана механизма по формуле (4) с использованием формулы (5) в положении, изображённом на рис. 3, показал, что J = 0. Следовательно, это положение является особым. В таком положении происходит потеря управляемости механизма по углу ^ .