Моделирование распределения температуры при нагреве пластины с применением смешанного уравнения теплопроводности

Работа выполнена при финансовой поддержке гранта РНФ № 23-21-00269,

Расчет полей температуры с помощью обобщения закона Фурье часто применяют для процессов, которые протекают за короткий промежуток времени (при наносекундных лазерных высокоинтенсивных воздействиях), при исследовании импульсных процессов нагрева пластин (плазменная обработка материалов, импульсный нагрев плат микросхем и т. д.) [1].

При этом фронт возникающей тепловой волны описывают через гиперболическое уравнение теплопроводности. Это уравнение показывает распределение тепловых волн с конечной скоростью в отличие от параболического случая для обычного закона Фурье [2, 3].

Применение смешанного уравнения теплопроводности необходимо для включения в численный расчет процесса импульсного нагрева, описываемого гиперболическим уравнением, квазистационарного этапа пока еще холодной пластины. Это выяснит изменение полей температуры с возникновением так называемого времени релаксации теплового потока для существенно нестационарного нагрева [4].

В данной статье исследуем задачу нахождения температурного распределения в пластине, бесконечной по двум пространственным переменным, с импульсным нагревом её в промежуточный момент времени и выполнением краевых условий на потоки тепла 3-го рода. Изучим полученную математическую модель, используя как линейное, так и нелинейное смешанные уравнения теплопроводности и применяя метод теплового баланса.

• 1    Линейная задача

Рассматривается бесконечная пластина по осям y и z , с постоянной шириной по оси x размером X , с однородными физическими характеристиками. При этом в численном расчете переменные y и z не будем упоминать в списке, считая их просто параметрами. Начальное распределение температуры внутри пластины описывается функцией uo(x) в момент времени T1 . Потоки тепла окружающей среды на боковых границах пластины обозначены как q0 на левой стороне и qX на правой. Теплообмен между пластиной и окружающей средой подчиняется закону Ньютона (граничные условия третьего рода). Необходимо найти поле температуры внутри пластины в зависимости от координаты x в любой момент времени от T1 до T2 . Даны теплофизические свойства материала: удельная теплоемкость при постоянном объеме cv , удельная плотность ρ, коэффициент теплопроводности λ, коэффициенты теплопередачи α0 и αX на боковых границах пластины, коэффициент внутреннего теплоотвода c и внутренний источник тепла f (x,t).

k(x, t)u tt + C v (x, t) • p(x, t)u t = (A(x, t)u x ) x + c(x, t)u + f (x, t) (1)

x = о : -A(0, t)du(0, t) + aou(O, t) = qo

∂x x = X : A(X,t)du(X,t) + axu(X,t)= qx(3)

∂x

u(x,t)|t=Ti = uo(x).(4)

При работе с уравнениями, содержащими переменные коэффициенты (1), и особенно с нелинейными уравнениями, замена производных конечными разностями может привести к появлению значительной погрешности или к несостоятельности схемы. В таких случаях предпочтительно использовать консервативные разностные схемы. Для обеспечения соответствия разностных схем законам сохранения энергии, массы и количества движения важно, чтобы полученные дифференциальные уравнения отражали основные законы сохранения для произвольного объема сплошной среды. Очевидно, что для получения разностного решения, которое точно описывает процесс изменения температурного поля как количественно, так и качественно, важно требовать выполнения закона сохранения энергии [4].

Для устойчивого разностного решения необходимо обеспечить выполнение закона сохранения для каждого элементарного объема, а также для любой области, составленной из этих объемов. Для этого требуется равенство значений тепловых потоков через общие границы соседних объемов для интегро-интерполяционного метода.

Следует подчеркнуть, что для достижения достоверности результатов при использовании метода теплового баланса обязательным является строгое соблюдение установленных критериев, когда максимальные габариты разбиений стремятся к нулю. Такой подход обеспечивает верифицируемость получаемых решений даже в условиях применения относительно крупных сеток, что особенно актуально для неявных разностных схем.

Эффективный коэффициент теплопроводности в линейном случае (1) будем вычислять по формуле:

^{A (} x i ^,t j ) , ± 2

[A((i ± 1) • h,T i + j • т ) + A(i • h,T i + j • т )] 2

Консервативная неявная разностная схема выглядит так:

, /    , x u i,j +1 ^{2 u} i,j ⁺ u i,j-1 . /     , \ ^ui,j +1 ^u i,j

k(x i ,t j ) —-------₂------+ a(x i ,t j ) —------- - =

= (A(x , ,t j ) _i+ 1 u - ⁺¹ - ⁺¹ - j - A(x_bt , ) ,- 1 j    -^{1 j+1} )1+

2 h                       2 h         h

+ c(x , ,t j )u ,,j +1 + I I       f (x,t)dxdt. (5)

tj    xXi-1/2

Рассмотрим разностную схему (5) и её численную реализацию в программной среде Mathcad-15 в области G = [0, X] x [T 1 , T 2 ]. T 1 < 0, T 2 > 0. Для исследуемой физической модели, a(x, t) = c v • p, V (x, t) € G; k(x, t) = 0, f (x, t) = f 1(x, t) = 0, t <  0; k(x, t) > 0, f (x, t) = f 2(x, t) > 0, t >  0, т. е. при t <  0 имеем классическое параболическое уравнение теплопроводности, а при t >  0 — гиперболическое уравнение. Приведем постановку смешанной задачи (1)–(4) со следующими конкретными расчетными данными [5].

Постановка начально-краевой задачи

Рассмотрим задачу(1)–(4). Найти распределение температурного поля в указанной бесконечной пластине с X = п и временем расчета: T 1 = - 5, T 2 = 20. Начальное условие:

u(x,t) | t = _{T 1} = u g (x) = 10sin(x).

Краевые условия (2),(3): q o = 5, q x = 10, a g = 3.5, а х = 3.5; коэффициенты: k = 0 при t <  0, k = 1 при t>0, c = 0, A = 3, a = 672.

Источник тепла: f 1(x,t) = 0, f2(x,t) = 100000sin(x)sin(t).

Приведенная неявная разностная схема решается с помощью метода теплового баланса.

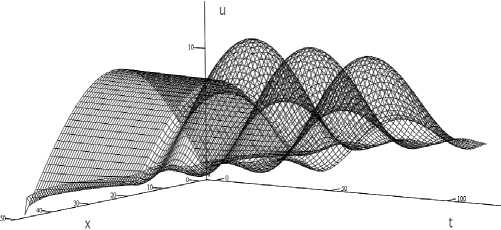
Рис. 1. График решения линейного уравнения

График численного решения этой задачи хорошо согласуется в параболической части с экспериментальными результатами [6]. Также для этих значений коэффициентов легко показать с помощью метода априорных оценок [7], что для внутреннего источника тепла f Е W 1 (G) существует единственное поле температуры u(x, t) этой смешанной краевой задачи из пространства W 2 (G), причем интерполяции u h дискретных значений разностной задачи сходятся слабо к решению u(x,t) в W^(G) при стремлении h и т к нулю.

• 2    Нелинейная задача

Необходимость решения нелинейных задач появляется при исследовании процессов, в которых наблюдается широкий диапазон температур. Скажем, теплопроводность сталей, применяемых в конструкциях криогенных систем, изменяется от 1 до 15 Вт/(м · К) на отрезке возрастания температуры от 5К до 300К.

При аналитическом решении нелинейных задач встречаются математические трудности, требующие специальных методов. Точная формула решения и метод её нахождения зависят от функционального описания нелинейностей в дифференциальных уравнениях и граничных условиях. Численное же решение нелинейных задач в этом плане гораздо проще. Алгоритмы их численного решения можно относительно легко построить, опираясь на конечно-разностные схемы, использованные как для линейных задач, так и для нелинейных [8]. Применим эти методы на примере следующего нелинейного уравнения:

k(x, t)u tt + C v (x, t) • p(x, t)u t = (A(u, x, t)u x ) x + c(x, t)u + f (x, t), (6) где A(u, x,t) — нелинейная функция температуры, описывающая эффективный коэффициент теплопроводности по формуле:

^A(u i,j +1 , ^x i , t j +1 ) i ± 1

[ ^A(u i± 1 ,j +1 , ^x i ± 1 , t j +1 ) + ^A(u i,j +1 , x i , t j +1 ^)]

.

Разностное уравнение для (6) с учетом теплового баланса теперь будет выглядеть так:

, j          x ^u i,j +1     ^{2 u} i,j + ^u i,j - 1 .   /    ,    \ ^u i,j +1     ^u i,j

k(x i , t j +i ) —------- Т2Г --------+ a(x i , t j +1 )       _T ----~ =

(A(u i,j +i , x i , t j +i ⁾ i + 1

u i +1 ,j +1    u i,j +1

h

x,             , X      ^u i,j +1   u i- 1 ,j +1x 1

^{A ( u} i ^{,j +1} , x i , ^{t j +1 )} i — 2           h         ) h +

+ c(x i ,t j +1 )U i,j +1 + I I      f (x,t)dxdt.

Jtj    xXi-1/2

Рассмотрим задачу (6),(2),(3),(4) с нелинейной теплопроводностью, но с аналогичными начальными и краевыми условиями по консервативной разностной схеме(7), где X(u, x, t) = 0, 5 • u ² + 2. Метод Ньютона используется для линеаризации разностной схемы в случае, когда коэффициенты зависят от температуры по степенным функциям и могут быть дифференцированы. Величина u на этой итерации u _i ^s выглядит так:

u s = u S ^{- 1} +Au s^s ,                         (8)

i где s — номер итерации, AuS — приращение температуры на s-й итерации. Заменим функцию λ уравнением, найденным через разложение в ряд Тейлора в точке uS — 1:

/^{S - 1}

\ s = A ss^-1 + d^ Au ss . (9) ^{i i} ∂u ⁱ

Производная в уравнении (9) рассчитывается на основе значений u на прошлой итерации. Следовательно, в правой части уравнения (9) неизвестным остаётся только Au i . Подставляя уравнения (9) и (8) в систему нелинейных разностных уравнений и пренебрегая членами, содержащими ( (Au S ) ² , мы получаем систему линейных уравнений для приращений Au S . Данная система характеризуется трехдиагональной матрицей и может быть решена с использованием прогоночных методов.

При использовании метода Ньютона для линеаризации на каждом шаге решается задача относительно изменений Au S . Следующими определяются значения u _i ^s в соответствии с уравнением (8).Итерации прекращаем при достижении заданной точности. Данный метод демонстрирует более высокую скорость сходимости в сравнении с методом простых итераций, однако он требует больших усилий при программной реализации, а также подразумевает вычисление производных от функции теплопроводности λ [9].

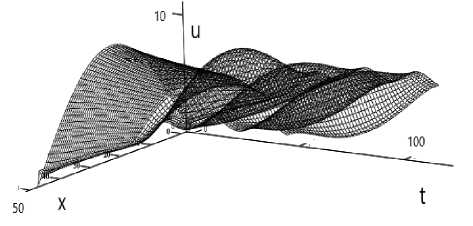
Рис. 2. График решения нелинейного уравнения

График численного решения этой задачи в программном пакете Mathcad 15 в нелинейном случае приводится на рис. 2, который отображает важные особенности решения в линейном случае.

Заключение

Численное решение поставленных корректно краевых задач для предложенного гиперболо-параболического уравнения как в линейном, так и в нелинейном случае с помощью консервативной схемы позволяет довольно точно описать процессы, связанные с нагревом указанной пластины. При этом расчет проводится в широко распространённой сейчас, достаточно доступной и наглядной в инженерных расчетах программной среде Mathcad-15. В дальнейшем будет разработана программа для многослойных ограниченных пластин из композиционных материалов и использована эта математическая модель для решения широкого спектра физических задач с двумя и тремя пространственными переменными в анизотропном случае с общими краевыми условиями третьего рода по всем координатам.