Моделирование распространения сетевого вируса в локальной компьютерной сети методами теории перколяции

Чтобы просмотреть копию этой лицензии, посетите

Стремительное развитие информационных технологий сопровождается постоянным обменом информацией, что, в свою очередь, сопровождается и распространением компьютерных вирусов. Несмотря на богатство антивирусных программ, каждый день возникают все новые и новые угрозы. Актуальным является изучение распространения вирусов в компьютерных сетях с целью его своевременного обнаружения, предотвращения и дальнейшей защиты.

Начало всех исследований в области компьютерной вирусологии было положено в 1940-х гг., когда Джон фон Нейман поставил перед собой задачу построения модели машины, сложность которой могла бы возрастать подобно биологическим организмам в условиях естественного отбора. Предположительно, такая задача была поставлена для того, чтобы вычислительные машины смогли развиваться самостоятельно с течением времени. Но на тот момент не было реализации подобной модели, поэтому в данном направлении проводились дополнительные исследования.

Первая попытка реализации была совершена Лайонелом Пенроузом в 1957 г. Английский психиатр, медицинский генетик и математик впервые показал пример самовос-производящейся механической структуры [1]. Логическая часть его идеи была основана теории фон Неймана, а физическая часть заключалась в том, чтобы создать простые блоки или кирпичики с такими свойствами, чтобы из них можно было построить самовоспроизво-дящийся механизм.

Спустя несколько лет в 1966 г. Артур Беркс опубликовал книгу "Теория самовос-производящихся автоматов" на основе лекций фон Неймана [2], в которой были изложены основные идеи для реализации такого механизма в машинной среде.

В настоящее время компьютерный вирус определяется как программа, целью которой является распространение своих копий. Компьютерные вирусы классифицируются по признакам среды обитания, способу заражения, методам распространения, организации программного кода и деструктивным возможностям [3].

Развитие информационных сетей, объединяющих несколько рядом стоящих компьютеров, способствовало появлению вируса, представляющего угрозу компьютерной инфраструктуре, в которой находятся десятки или даже сотни работающих вычислительных устройств. В отличие от загрузочных и файловых вирусов, сетевой вид обладает свойством самораспространения без использования внешних устройств передачи данных. Такой вид относят к классу вирусов-червей. Проводятся исследования по изучения распространения вирусов [например, 4–9]. Разными авторами предложены оригинальные и модифицированные эпидемиологические модели. При анализе работ в данном направлении наблюдается тенденция к востребованности методов теории перколяции. Использование перколяционных свойств для большого разнообразия существующих архитектур компьютерных сетей и методов атак злоумышленников может способствовать совершенствованию методов антивирусной защиты от нападения, вследствие чего снизится количество успешных атак на информационную инфраструктуру.

Целью настоящей работы является исследование распространения сетевого вируса в локальной сети с использованием подходов теории перколяции. Для достижения цели авторами были предложены и исследованы две перколяционные модели распространения сетевого вируса в локальной компьютерной сети, описывающие два вида сетей: проводные и беспроводные. Порог перколяции соответствует доле зараженных компьютеров в сети, при которой сеть теряет работоспособность.

Постановка задачи

В рамках данной работы предложены и исследованы две решеточные перколяционные модели распространения сетевого вируса в локальной компьютерной сети, описывающие два вида сетей: беспроводные и проводные.

В первой модели беспроводная локальная сеть представлена в виде наиболее распростра- ненной сети ячеистой топологии, которая описывается простой квадратной решеткой.

Линейный размер решетки - N. Компьютеры в локальной сети - узлы решетки, которые могут быть свободными (не зараженными вирусом) и занятыми (зараженными вирусом). Свободным узлом считается компьютер, сохраняющий полную работоспособность и никак не влияющий на работу соседних компьютеров.

Под занятым узлом подразумевается, что компьютер имеет вредоносный код, способный причинить вред компьютеру, а также передавать свою копию соседним компьютерам. При этом такой компьютер продолжает работать. Один компьютер может заразить другой компьютер, то есть если текущий узел занят, то соседние с ним узлы могут стать занятыми с вероятностью q 1. Кроме того, учитывается способность компьютера к восстановлению, то есть занятый узел может стать свободным с вероятностью q 2. Восстановление возвращает узлу свободное состояние и освобождает компьютер от вредоносного кода.

Соседние занятые узлы образуют кластеры - группы зараженных компьютеров. Концентрация занятых узлов p соответствует степени распространения вируса в локальной сети. Если в системе находится непрерывная группа зараженных компьютеров, проходящих через всю сеть (перколяционный кластер), то можно говорить о наличии перколяции - просачивании сетевого вируса через всю локальную сеть, что означает возможность выхода вируса за пределы локальной сети и блокировку передачи информации между любыми свободными узлами. В модели были применены открытые и периодические граничные условия (ОГУ и ПГУ соответственно). Математически предложенную модель можно описать так:

Ж = N.p. qt^k , где к - количество испытаний.

Во второй модели применяется локальная сеть, использующая смешанную топологию из трех базовых: "Шина", "Кольцо", "Звезда". Общей сетью является шинная топология, объединяющая в себе множество N подсетей, представленных кольцевой и звездной топологиями. В свою очередь каждая подсеть состоит из z узлов. Граничащие между топологиями узлы являются коммутаторами и обеспечивают связь с соседними локальными сетями. Начало и конец сети определяется первой и последней подсетью соответственно (см. рис. 1).

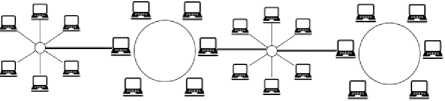
Рис. 1. Пример смешанной сети второй модели

Математически модель записывается следующим образом:

М2 = < N,z,p,k >.

Основной задачей в рамках каждой из предложенной модели является получение оценки значения порога перколяции при различных параметрах модели. Под порогом перколяции принимается значение концентрации занятых узлов, при которой вероятность возникновения стягивающего кластера равна 0.5. Порог перколяции соответствует критической концентрации зараженных компьютеров локальной сети, при которой сеть теряет свою работоспособность.

Методы исследования

Для моделей были разработаны и реализованы алгоритмы распространения занятых узлов, поиска кластеров и определения наличия перколяции в системе. Были написаны программы на языке программирования C++ с консольным интерфейсом.

Для первой модели алгоритм заполнения квадратной решетки свободными и занятыми узлами описан ниже.

• 1.    Из всех узлов случайно выбирается первый занятый узел.

• 2.    Соседние свободные узлы текущих занятых становятся занятыми с вероятностью q 1.

• 3.    Занятые узлы могут стать свободными с вероятностью q 2.

• 4.    Повторить 2-3 до достижения необходимой концентрации занятых узлов на решетке.

Для маркировки кластеров на решетке используется алгоритм Хошена–Копельмана [10]. Для поиска перколяционного кластера используется алгоритм "поиска в глубину" [11]. Для обеспечения коэффициентов вероятности используется генератор псевдослучайных чисел "Вихрь Мерсена" [12].

Для второй модели разработан следующий алгоритм определения порога перколяции проводилось путем проведения к случайных экспериментов, в каждом из которых:

• 1)    случайным образом конфигурируется общая сеть, состоящая из N подсетей,

• 2)    для каждой подсети находится свой порог перколяции,

• 3)    находится среднее значение порога перколяции для общей сети.

После чего полученные значения по к экспериментам усредняются.

Порог перколяции для подсетей кольцевой или звездной топологии находятся аналитически. Рассмотрим кольцевую подсеть. Подсеть имеет граничные узлы, которые обеспечивают внешнюю связь с соседними подсетями. Однако внутри возникает два пути распространения вируса: верхняя и нижняя цепочка (см. рис. 1). Данные цепочки являются одномерными, порог перколяции для каждого пути pc = 1, так как кластер из занятых узлов может возникнуть, только если все узлы хотя бы в одной из цепочек заняты [13]. Таким образом, подсеть имеет точное значение порога перколяции pc = 1.

Звездная топология имеет похожую структуру с деревом Кейли или решеткой Бете. Подсеть представляет первый уровень построения дерева Кейли, когда из одного узла выходит z новых узлов. Для такой структуры вычислена и доказана критическая концентрация pc =1/( z -1) в [14]. Подставляя значение количества выходящих узлов в данную формулу, можно точно определить критическую концентрацию в подсети.

Далее, чтобы найти порог перколяции для общей сети, необходимо сложить критические концентрации p 1 c , p 2 c , ..., pNc и разделить на количество подсетей N .

Численные эксперименты основаны на подходах методов Монте-Карло с применением методов математической статистики и теории вероятностей.

Результаты и их обсуждение

Для первой модели проведен ряд численных экспериментов со следующими параметрами: N = 10; 20; 50 ; р = 0 0,1.,, 1 q_Y = 0,5 ; q₂ = 0; 0,1;...; 0,6 . Значение q_r выбрано, исходя из неопределенного количества внешних факторов, а также человеческого фактора. Поэтому вероятность заразить или не заразить компьютер является одинаковой.

Параметр q~ имеет диапазон значений: от низкой эффективности каких-либо противодействующих средств либо их отсутствия до наличия эффективных средств защиты компьютера.

Для каждого набора входных данных было проведено 1000 экспериментов и определено значение порога перколяции по следующей методике: определяется вероятность возникновения перколяционного кластера P(p) .

Полученные в ходе компьютерного эксперимента значения вероятности возникновения перколяционного кластера РРр'} для каждого набора данных при различных значениях Л' и q^ аппроксимируются сигмоидальной функцией:

Р(р) = (1 +ехр (-(р - р^а) )^-1.

Значение доли заполненных узлов p , при которой вероятность появления перколяционного кластера равна 0.5, является значением порога перколяции (например, рис. 2).

При аппроксимации данных возникает погрешность: при численном эксперименте учитывается погрешность вероятности возникновения перколяционного кластера при каждом значении концентрации занятых узлов с использованием стандартного отклонения среднего 'J_? = ~lp_qP; - Р^/ к.

Погрешность значения порога перколяции - это результат аппроксимации данных в математическом пакете с учетом ошибок исходных данных.

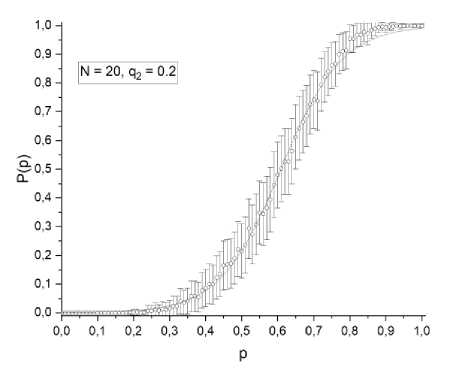
Рис. 2. Вероятность возникновения стягивающего кластера, при N = 20;   =0,5;

с открытыми граничными условиями

Найдены значения порогов перколяции для выбранных входных параметров модели при открытых и периодических граничных условиях для систем конечного размера, дан- ные представлены в табл. 1. Пустые ячейки означают, что для соответствующих входных параметров перколяция не наступила.

Таблица 1. Значения порога перколяции с погрешностью аппроксимации при различных N и q₂ с открытыми и периодическими граничными условиями

0,6	0,5	0,4	0,3	0,2	0,1	0	42
–	–	–	0,789 (0,001)	0,6332 (0,0009)	0,5356 (0,0009)	0,4735 (0,0008)	N = 10 ОГУ
–	–	0,876 (0,001)	0,679 (0,001)	0,5453 (0,0008)	0,4608 (0,0006)	0,4052 (0,0006)	N = 10 ПГУ
–	–	–	0,7922 (0,0009)	0,6089 (0,0009)	0,5056 (0,0007)	0,4472 (0,0006)	N = 20 ОГУ
–	–	0,9885 (0,0009)	0,747 (0,001)	0,5561 (0,0008)	0,4545 (0,0005)	0,4000 (0,0005)	N = 20 ПГУ
–	–	–	0,8037 (0,0007)	0,587 (0,001)	0,4591 (0,006)	0,4108 (0,0006)	N = 50 ОГУ
–	–	–	0,7935 (0,0005)	0,5602 (0,0007)	0,4350 (0,0006)	0,3910 (0,0004)	N = 50 ПГУ

При увеличении значения параметра q₂ вероятность появления перколяционного кластера значительно снижается. При этом наблюдается разделение значений Qz на две группы. Первая группа достигает значения порога перколяции и представляет достаточную опасность для компьютерной сети. В нее входят модели при q₂ = 0; 0,1; 0,2; 0,3. Вторая группа содержит модели при q₂ = 0,4; 0,5; 0,6, которые не так опасны для компьютерной сети. При максимальной концентрации узлов вероятность появления перколяционного кластера находится ниже значения 0,5. Стоит отметить, что модель с параметром 9г > Qi на всем диапазоне концентрации p имеет вероятность P(p) близкую к нулю, что является адекватным результатом, так как восстановление узлов происходит интенсивнее, чем заражение.

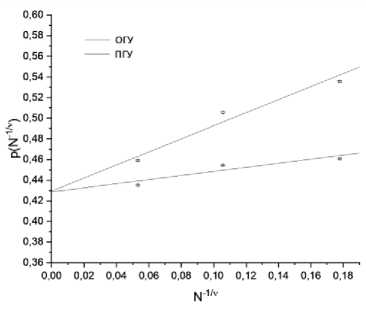
Рис. 3. Определение порога перколяции для случая бесконечной системы с помощью скейлинга при

Q2 =0,1

Для бесконечного случая определены значения порога перколяции с помощью скей-лингового соотношения (например, рис. 3), результаты для открытых и периодических граничных условий представлены в табл. 2. Близкие или схожие значения для разных граничных условий говорят о правильности полученных результатов, так как порог перколяции для бесконечной перколяционной системы не должен зависеть от этого параметра.

Таблица 2. Значения порогов перколяции для случая бесконечной системы

42	Scaling, ОГУ	Scaling, ПГУ
0	0,387 (0,11)	0,385 (0,03)
0,1	0,429 (0,15)	0,429 (0,10)
0,2	0,569 (0,003)	0,567 (0,002)
0,3	0,809 (0,005)	0,828 (0,005)
0,4	–	–
0,5	–	–
0,6	–	–

Для второй модели проведен ряд численных экспериментов со следующими параметрами: N= 5; 10; 20; 50; 100; 200 ; Z= 0...100; k = 1000 . Оба параметра представляют собой расширенный диапазон размерностей общей сети и подсети: от малых размеров до больших. Значения порога перколяции представлены на рис. 3.

Полученные результаты показывают, что при увеличении количества узлов в подсетях порог перколяции снижается достаточно быстро и постепенно приближается к значению 0.5.

С увеличением значения параметра N кривые на рисунке становятся сглаженнее и описывают практически одинаковы значения, что говорит о том, что количество узлов в подсетях не является определяющим при большом количестве испытаний.

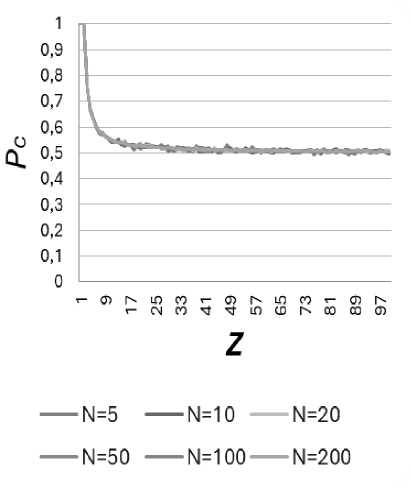
Рис. 3. Сравнительный график значений порога перколяции между различными N

Исходя из вышеописанного, значение pc = 0.5 можно взять за значение порога перколяции для бесконечного случая.

Заключение

В рамках данной работы проведено моделирование распространения сетевого вируса в локальной компьютерной сети с применением теории перколяции. Были разработаны две модели: модель поведения сетевого вируса в беспроводной локальной сети с учетом способности вычислительного узла к восстановлению; модель, использующая смешанную топологию локальной сети.

Результаты исследования первой модели показывают, что при отсутствии возможности восстановления зараженных узлов компьютерная сеть довольно быстро подвергается заражению и теряет свою работоспособность. Однако, если компьютеры имеют механизм восстановления после заражения, то риск полного заражения локальной сети значительно снижается.

По результатам второй модели был определен порог перколяции pc = 0.5 для бесконечной системы.