Моделирование разрушения упругопластических тел
Автор: Бураго Николай Георгиевич
Журнал: Вычислительная механика сплошных сред @journal-icmm
Статья в выпуске: 4 т.1, 2008 года.
Бесплатный доступ
Рассмотрены имеющиеся подходы к расчету разрушения. Описана теоретическая модель, численный метод и результаты расчета разрушения растягиваемых образцов из упругопластического материала с макропорами и жесткими включениями. Макропоры рассмотрены непосредственно как полости в сплошной среде, имеющие круглую или эллиптическую, ориентированную под некоторым углом, форму. Материал подчиняется уравнениям теории упругопластического течения, дополненным кинетическим уравнением для поврежденности и зависимостью модулей упругости и предела текучести от поврежденности. Рост поврежденности происходит при выполнении условия начала разрушения, которое выражает достижение максимальной главной деформацией предельной величины. С ростом поврежденности модули упругости и предел текучести стремятся к нулю, что означает постепенную потерю материалом несущей способности в зоне запредельных деформаций. Исследовано влияние макропор и жестких включений на пространственно осредненные диаграммы растяжения. На основании численных экспериментов даны рекомендации по выбору свойств методов моделирования процессов разрушения, которые желательны для обеспечения достоверности численных решений
Короткий адрес: https://sciup.org/14320447
IDR: 14320447
Текст научной статьи Моделирование разрушения упругопластических тел
Под разрушением понимается явление, выражающееся в образовании трещин в структурированных телах, приводящее к их фрагментации, то есть к разделению на части. В простейшем подходе, используемом в теории сопротивления материалов, трещины не рассматриваются, и учет разрушения сводится к оценке коэффициентов запаса прочности путем сравнения максимальных расчетных напряжений с их предельными значениями, предсказываемыми так называемыми теориями прочности [1].
Нередко интерес представляет не только оценка прочности, но и предсказание сценариев развития разрушения, определение времени разрушения, определение влияния различных изменений в конструкциях и материалах на процессы разрушения, предсказание свойств материала в процессе накопления внутренних дефектов. Этот интерес стимулировал развитие механики разрушения.
В механике хрупкого разрушения полагается, что распространение трещины происходит при выполнении критерия разрушения, сформулированного в терминах коэффициентов интенсивности напряжений. Расчеты распространения трещин проводятся с явным рассмотрением вновь образующихся поверхностей с использованием методов граничных или конечных элементов. Обзор работ по реализации подхода механики хрупкого разрушения сделан в [2].
В настоящее время предпочтение часто отдается методам сквозного счета, в которых разрушенные и неразрушенные ячейки рассчитываются по единому алгоритму. Разрушение учитывается корректировкой напряженного состояния в разрушенных ячейках. Впервые численная реализация этого подхода сделана в работе [3] и получила широкое распространение из-за своей простоты. Известно множество модификаций подхода, таких как метод «схлопывания» разрушенных ячеек [4], метод автоматизированного введения дополнительных узлов с образованием свободных поверхностей в разрушенных ячейках [5]. Расчеты напряженно-деформированного состояния в неразрушенных ячейках проводятся по обычным уравнениям теории упругости и пластичности. Интегральные эффекты разупрочнения, то есть уменьшения сопротивления тела деформации, получаются в расчетах как результат роста количества разрушенных ячеек.
Эксперименты показывают наличие на диаграммах деформирования участков разупрочнения, на которых наблюдается падение напряжений при росте деформации. Однако такие диаграммы с участками разупрочнения не могут считаться характеристиками материала и закладываться в этом качестве в расчеты явлений разрушения в рамках классической теории упругопластичности. Этому есть две причины. Первая причина заключается в том, что ниспадающие диаграммы характеризуют отнюдь не поведение материала в бесконечно малой окрестности материальной точки, а демонстрируют интегральную диаграмму деформирования экспериментального образца, то есть, на самом деле имеет место не реологическая неустойчивость, а конструкционная. Вторая причина заключается в том, что начальнокраевые задачи для системы уравнений упругопластичности на участках разупрочнения становятся некорректными. Действительно, в традиционных тензорных обозначениях уравнения упругопластичности имеют вид:
∂ t σ = E :( ∂ t ε -∂ t ε p ),
∂ t ε = ( ∂ x v ) s , ∂ t ε p = H (|| σ || -σ s ) λ ( σ , ε ): ∂ t ε,
ρ∂ t v = ∂ x σ ;
или
∂ t σ = E ( ep )( ε , ε p ): ∂ x v ,
{ ρ∂ t v =∂ x σ .
Здесь символ « : » обозначает двойное скалярное произведение тензоров.
Начально-краевые задачи становятся некорректными из-за нарушения на участках разупрочнения критерия Адамара
∂tσ:∂tε=(E(ep):∂xv):∂xv>0, называемого в механике критерием Драккера устойчивости материала. Нарушение критерия Адамара означает потерю свойства непрерывной зависимости решения от входных данных, а также утрату свойства гиперболичности в динамике и свойства эллиптичности в статике. В численном расчете при этом происходит переполнение арифметического устройства или получаются бессмысленные результаты, демонстрирующие отсутствие сходимости решения.
В цитированных выше работах по расчету разрушения реализуется мгновенная корректировка напряжений и мгновенное образование новых поверхностей распространяющейся трещины, поэтому участок разупрочнения благополучно пропускается благодаря скачкообразному изменению состояния. При вязком разрушении необходимо обеспечить расчет участков разупрочнения. Чтобы сделать теорию упругости и пластичности пригодной для описания разупрочнения, в [6, 7] предложено связать деградацию свойств упругости с параметром разрушения, который получил название повреждаемости. На необходимость введения такого дополнительного, связанного с разрушением, параметра состояния как количественной меры нарушений сплошности структурированной среды указывает тот факт, что образование и накопление микроповреждений и потеря свойств упругости происходят не только при достижении критического напряженно-деформированного состояния, но также из-за причин или воздействий нетермомеханической природы, таких как лазерное излучение, химические реакции и тому подобных. Поэтому накопление повреждений (микропор и микротрещин) трактуется как термодинамически независимый процесс. Считается, что повреждаемость для неповрежденного материала равняется нулю и растет по мере накопления микроповреждений сплошности материала.
Термодинамическая независимость процесса разрушения от процессов нагрева и деформации не исключает их взаимовлияния. Тензорная природа поврежденности может быть различной; известны попытки представления ее скаляром (наиболее часто), тензорами второго и четвертого рангов [8].
С ростом повреждаемости характеристики упругости материала, каковыми являются модули упругости и предел текучести, уменьшаются вплоть до нуля (вместе или в отдельности), что означает полное разрушение структурированного материала. При разрушении образуются новые макроповерхности разрыва сплошности (макротрещины) и происходит разделение деформируемого тела на части или даже на отдельные материальные частицы. Обзоры исследований и подробное обсуждение различных вариантов теории повреждаемости приводятся в работах [8–18], наиболее важные результаты которых рассматриваются ниже.
Введение независимого термодинамического параметра поврежденности как величины, отвечающей за уменьшение параметров упругости, устраняет проблему некорректности краевых задач при разупрочнении. Действительно, уравнения теории повреждаемости имеют вид модифицированных уравнений упругопластичности
∂ t σ = E ( ep ): ∂ x v + ( ∂θ E ∂ t γ ): ( E - 1 : σ ) +∂ x ⋅ ( νσ∂ x σ ),
ρ∂v=∂ σ+∂ ⋅(ρν ∂ v),
txxvx
∂tγ=H(Φγ)λγ(σ,ε,γ)+λ(γ0)(x,t)+∂x⋅(νγ∂xγ), где символ «⋅ » обозначает скалярное произведение тензоров; γ — параметр поврежденности; Φθ(σ,ε,γ,...,T,...) ≥0 — критерий начала разрушения; члены с вторыми производными по пространству комментируются ниже. Третье из приведенных уравнений описывает кинетику поврежденности. Первый член в этом уравнении отвечает за рост поврежденности вследствие нагрева и деформирования, второй член — за рост поврежденности из-за нетермомеханических воздействий.
На участках разупрочнения критерий Драккера в теориях повреждаемости по-прежнему нарушается (материал неустойчив):
∂tσ:∂tε=(E(ep):∂xv):∂xv+(∂σ/∂γ)∂tγ:∂xv≤0, но разупрочнение (отрицательность левой части) вызывается не отрицательной определенностью упругопластического оператора E(ep) в первом слагаемом правой части, а вторым слагаемым, которое для активного процесса роста повреждаемости является отрицательным и большим по модулю, чем первое слагаемое. Так что теперь критерий Адамара не нарушается
(E(ep):∂xv):∂xv>0, поскольку в расчет закладывается диаграмма деформирования (или какая-либо другая форма закона упрочнения) без участков разупрочнения, а эффект разупрочнения — это проявление роста повреждаемости и деградации упругости.
Теперь следует прокомментировать появление дополнительных членов со вторыми пространственными производными. В основном варианте теорий повреждаемости члены с вторыми производными от основных искомых функций в уравнениях отсутствуют. Они возникают в градиентных теориях и интегральных теориях осреднения [18] упругопластичности и повреждаемости. Множители ν с индексами σ , v , γ являются коэффициентами вязкости («градиентной вязкости»). Дополнительные члены градиентных теорий придают уравнениям теории повреждаемости параболические свойства, улучшают их свойства, сглаживают решения и являются, таким образом, регуляризаторами (то есть, членами, улучшающими обусловленность задач). Физически обоснованные значения коэффициентов градиентной вязкости настолько малы, что регуляризаторами служить не могут, поэтому в численном решении при необходимости регуляризации градиентная вязкость искусственно увеличивается до значений, не нарушающих обычные курантовские ограничения шагов по времени в явных разностных схемах, то есть до значений c 2 Δ t /2 , где с — скорость звука, Δ t — шаг по времени.
Роль параметра, меняющегося независимо от деформации и ответственного за деградацию свойств упругости, помимо собственно параметра поврежденности, могут играть также и другие параметры состояния, такие, например, как температура и пористость. В моделях упруговязкопластических сред, в которых приращения пластической деформации не связаны напрямую с приращениями полной деформации, деградацию свойств упругости можно связать непосредственно с ростом пластической деформации без риска потери корректности краевых задач.
При расчете разрушения на каждом шаге инкрементальных (пошаговых) методов уравнения упругости и пластичности используются с диаграммами деформирования без участков разупрочнения, но с разным уровнем значений модулей упругости и предела текучести в зависимости от поврежденности или другого, не связанного напрямую с деформациями, параметра, ответственного за разупрочнение. Эффект разупрочнения не закладывается в математическую модель в виде зависимости предела текучести от деформации, а получается путем решения задачи в расширенном (поврежденностью) пространстве переменных состояния как результат роста поврежденности и соответствующей деградации упругих свойств материала. Таким образом, с математической точки зрения введение поврежденности является эффективной регуляризацией краевых задач упругопластичности для расчета неустойчивых режимов деформирования.
В расчетах по теориям поврежденности наблюдается развитие зон разрушения с пониженным упругим сопротивлением материала. В таких зонах интенсивность деформаций и поврежденность показывают всплеск, а перемещения и скорости претерпевают скачкообразное изменение, что имитирует расхождение берегов макротрещины. Краевые задачи при этом являются корректными, но обусловленность их с развитием зон разрушения ухудшается, что может приводить и приводит, если не принимать превентивных мер, к патологической зависимости результатов численного моделирования от параметров дискретизации, таких как форма и размеры расчетных ячеек в сеточных методах, распределение частиц в бессеточных методах, величина шага по времени.
Конечно, результаты численного моделирования всегда зависят от параметров дискретизации, но при измельчении сеток или при наращивании числа базисных функций эти решения должны демонстрировать сходимость решений к определенным, не зависящим от метода, пределам. Наличие сходимости и достоверность численных методов должны устанавливаться чисто математическими средствами, включающими априорный анализ методов на упрощенных модельных задачах и апостериорные проверки сходимости — на аналитических решениях, которые всегда можно получить искусственно, подставляя произвольное решения в уравнения и условия задачи и объявляя полученные невязки известными правыми частями. Для таких уравнений численный метод должен воспроизвести заложенное произвольное решение с достаточной точностью.
Проблемой большинства численных моделей разрушения является сильная зависимость решения от параметров дискретизации, таких как размер и форма ячеек сетки, или, в более общем смысле, зависимость решения от выбора базисных функций в проекционных методах, каковыми и являются по большому счету все используемые методы.
Справедливости ради необходимо заметить, что отсутствие сходимости или, яснее сказать, отсутствие повторяемости картины явления в малом (в деталях) свойственно и физическим экспериментам по разрушению. Это объясняется чувствительностью сценариев развития повреждений к неоднородности свойств реальных сред и к небольшим вариациям во внешних воздействиях.
Повторяющимися и воспроизводимыми характеристиками процессов разрушения могут являться их интегральные характеристики, например, интегральные (то есть усредненные по рассчитываемому объекту) диаграммы деформирования, энергия, затрачиваемая на разрушение деформируемого тела, время его жизни в определенных условиях нагружения. Результаты для таких интегральных характеристик при численном решении и в экспериментах должны демонстрировать сходимость. Для этого в численном моделировании надо принимать все меры для улучшения обусловленности (регуляризации) решаемых задач на режимах разрушения, не искажая, по возможности, самого решения этой регуляризацией.
Выше уже отмечены основные способы регуляризации краевых задач упругопластичности на режимах разупрочнения. Первый способ состоит в использовании не зависящего напрямую от деформации параметра поврежденности для учета деградации свойств упругости материала.
Второй способ в моделях упруговязкопластичности связывает деградацию свойств упругости при разрушении с ростом пластической деформации. Критерий Адамара для задач упруговязкопластического деформирования выполняется, поскольку пространственный оператор таких задач совпадает с оператором теории упругости.
Третий способ регуляризации используется в градиентных теориях повреждаемых упругопластических материалов, при этом улучшение обусловленности начальнокраевых задач достигается физически обоснованным пространственным осреднением зависимых переменных (напряжений, деформаций и поврежденности) в малой окрестности каждой точки. Такое осреднение эквивалентно сглаживанию решений введением в определяющие эволюционные уравнения инкрементальных теорий повреждаемой упругопластической среды дополнительных вязких членов для придания системе уравнений свойств параболичности.
Четвертый способ является дополнительным к каждому из трех, упомянутых выше, и состоит в учете сил инерции в задачах разрушения независимо от скорости нагружения. Учет инерции в задачах с пространственным оператором эллиптического типа предотвращает некорректность краевых задач для фрагментов, отделившихся от первоначального тела при его разрушении. Действительно, на режимах фрагментации деформируемое тело делится зонами разрушения на невзаимодействующие части. Статические краевые задачи становятся некорректными для частей, лишенных закреплений. Поэтому учет инерции, который устраняет эту некорректность, следует предусматривать в математических моделях расчета разрушения с самого начала.
Для обеспечения физической достоверности расчетов разрушения важной является проблема выбора критерия разрушения и описания кинетики накопления поврежденности. Эта проблема рассмотрена в [17].
На стадии конструирования численного алгоритма решения задач о разрушении возникает вопрос, какую, явную или неявную, схему решения принять к реализации. Считается, что явные схемы эффективны в задачах волновой динамики, а неявные схемы — в задачах квазистатики. В последнее время, благодаря появлению быстродействующих компьютеров, это представление меняется. Квазистатические задачи деформирования и континуального разрушения с успехом решаются с использованием явных схем [5] и, наоборот, в динамических задачах эффективно применяются неявные схемы [19].
Несмотря на обилие (многие тысячи!) работ, посвященных моделированию континуального разрушения, ясности в выборе математической модели, а также в построении методов ее регуляризации и реализации на сегодняшний день нет, и имеется больше вопросов, чем ответов. В настоящем кратком обзоре ссылки приводятся скорее для обозначения имеющихся направлений и освещены далеко не все подходы.
2. Постановка задачи
Полная система уравнений для моделирования разрушения, используемая в настоящей работе, является обычной системой уравнений теории упругопластического течения, дополненной кинетическим уравнением для поврежденности и зависимостью модулей упругости и предела текучести от поврежденности. Температурные эффекты не рассматриваются. Для малых деформаций эта система уравнений имеет вид:
ρ∂ t 2 U =∇⋅ σ , σ = E ( γ ) : ( ε - ε p ), ε = 1/2( ∇⊗ U + ( ∇⊗ U ) T ),
∂ F
∂ t ε p =λ p p H ( F p ) H ( σ: ∂ t ε ), F p ( σ ) = 3/2( σ ' :σ ')/ σ 2 p - 1,
∂ σ
∂tγ=H(Fd)Γ(ε,εp,γ)+rγ, Fd=Fd(ε,εp,γ), где ρ — плотность; U — вектор перемещений; σ — тензор напряжений; σ'=σ-(σ:I)I/3 — девиатор напряжений; E(γ) — тензор модулей упругости, зависящий от скалярной поврежденности γ ; ε — тензор деформации; ε p — тензор пластических деформаций; символ «⊗ » обозначает внешнее тензорное произведение; λp — коэффициент, определяемый условием пластичности Fp(σ)= 0; Fp — функция нагружения; H — функция Хевисайда, равная нулю для отрицательных значений аргумента и единице — в противном случае; σp — предел текучести; I — тензорная единица; Fd — функция условия разрушения, неотрицательные значения которой разрешают накопление поврежденности; rY — нетермомеханический (например, химический) источник поврежденности.
Система уравнений дополняется:
главными граничными условиями:
U ■ т J = U*(x, t) (а = 1,2), x∈∂Vuα
U ■ ni x ed V un = U n *(X , t ) ;
естественными граничными условиями:
а: n
⊗τα
x ed У та =а V\ a V u а
= p a ( x , t ),
° : n ® ni x ed V " =d V \ d V un
- p ^x, t ) ;
начальными условиями:
Ul t = 0 =d - Ul t = 0 = = , 1 , = 0 =Y t . . = °.
где n и т а ( а = 1, 2 ) — орты нормали и касательных к границе. В каждой точке границы заданы либо главные (кинематические), либо естественные (динамические) граничные условия. Заданные функции отмечены звездочками.
3. Метод решения
Задачи рассматриваются в пространственно двумерной постановке в условиях плоской деформации. Для решения применяется вариант метода конечных элементов [19].
По пространственным переменным ( x , у ) для всех искомых функций используется кусочно-линейная аппроксимация на треугольных и четырехугольных ячейках, по времени — неявная схема Эйлера. Шаг по времени ограничивается условием точности для того, чтобы поддерживать норму приращения решения на каждом шаге по времени малой по сравнению с нормой самого решения.
На каждом шаге по времени сначала решается обычная вспомогательная линеаризованная краевая задача теории упругопластичности относительно приращений перемещений при неизменном уровне поврежденности. Расписывать в подробностях эту хорошо известную задачу смысла нет, поэтому здесь приводится только ее общий вид в дифференциальной форме:
pA" (AT” - v") = ^ (° " +A’(AU "*')) (x e V), (U’ +AU’*')■ тa| „ = U*(x,t"+1) (a = 1,2), x∈∂Vuα
(U" +AU"+1) ■ n ”| = U„ (°" + A°(AU"+1)): n" ® т "| = p*(x, t"+1) (a = 1,2), al xedV„=дV\dVua aV 7 (σn+Δσ(ΔUn+1)):nn⊗nnx∈∂Vn=∂V\∂Vun=-pn*(x,tn+1), где Δσ(ΔUn+1 ) — линейный дифференциальный оператор, преобразующий приращения перемещений в приращения напряжений в соответствии с уравнениями теории упругопластического течения. Приращения перемещений определяются с помощью двойного итерационного процесса, состоящего из внешних итераций по нелинейности, то есть итераций по методу Ньютона, и из внутренних итераций решения систем линейных алгебраических уравнений методом сопряженных градиентов [19]. В расчетах методом конечных элементов записанные уравнения приводятся к вариационной форме баланса виртуальных работ. По найденным перемещениям на новом временном слое при t= tn+1с использованием исходных уравнений находятся последовательно новые значения деформаций, пластических деформаций и напряжений. Затем отдельно интегрируется кинетическое уравнение для поврежденности. Следует отметить некоторые особенности метода решения, обусловленные спецификой задач континуального разрушения. Рассматриваемые процессы до разрушения протекают довольно медленно и влиянием инерции в уравнениях движения, казалось бы, можно пренебречь. Однако с появлением зон разрушения процесс деформирования способен резко ускоряться, становясь в их окрестности динамическим. Заранее предсказать момент появления зон разрушения без проведения расчета невозможно, поэтому учет инерционных членов в алгоритме решения необходим с самого начала. Помимо корректного расчета динамики процесса в этом случае сохраняется корректность краевых задач и при фрагментации. Обилие нелинейных членов в уравнениях и приближенное решение нелинейных задач итерациями приводят к тому, что искомые функции претерпевают нефизические мелкомасштабные осцилляции в пространстве и времени. Признаком нефизических осцилляций (немонотонностей) решения является его колебательный характер с длинами полуволн, равными шагам пространственно-временной сетки. Такие немонотонности обнаруживаются по смене знака вторых производных от решения по отдельной координате в пределах одного ребра сетки (не обязательно расположенного вдоль координатной линии). Эти нефизические немонотонности должны немедленно устраняться, иначе в условиях плохой обусловленности задач на режимах разрушения они могут искажать численное решение, вызывая появление ложных зон разрушения. Монотонизация решений проводится в два этапа. На первом этапе используется «физический» способ сглаживания, основанный на введении в эволюционные определяющие уравнения для пластических деформаций и поврежденности малых сглаживающих вязких членов, что обосновывается градиентной теорией повреждающейся упругопластической среды: ∂F ∂tεp=λp pH(Fp)H(σ:∂tε)+∇⋅(ν∇εp), ∂σ ∂tγ=H(Fd)Γ(ε,εp,γ)+rγ +∇⋅(ν∇γ), где ν — коэффициент вязкости. На вопрос о величине коэффициента вязкости ν однозначного ответа не дает ни теория, ни эксперимент. Можно ожидать, что экспериментальные физические значения коэффициента вязкости будут слишком малыми для обеспечения эффективной монотонизации решения при реально используемых грубых дискретизациях. Так или иначе, в зависимости от явной или неявной аппроксимации диффузионных членов, на примере пространственно одномерных модельных задач несложно найти минимальные значения коэффициента вязкости, необходимые для уменьшения осцилляций численных решений в линейном случае. В наших расчетах это значение равняется v = c2At /2. Характерно, что эта вязкость уменьшает осцилляции, но не гарантирует их отсутствие. Поэтому далее решение подправляется дополнительно. На втором этапе используется «математический» способ сглаживания, заключающийся в устранении вновь появляющихся немонотонностей нелинейным сглаживанием. Для этого в конце каждого шага по времени для каждой сглаживаемой функции f находятся ее вторые производные fxx по каждому координатному направлению x из решения следующих вспомогательных задач: J (Vf-V5f„ + ^ 5f„) dV = 0, V fx I, V = 0; то есть вторые производные таким способом определяются в условиях простейшей аппроксимации решения кусочно-линейными функциями. При использовании квадратурных формул с точками интегрирования в узлах сетки матрица системы уравнений для вторых производных получается диагональной и легко обращается. Если на некотором ребре сетки величина fxx меняет знак, то в соседних узлах, определяющих данное ребро, проводится локальное сглаживание решения путем сдвига узлового значения функции fi к ее среднему значению по направлению x : f. := ((f. + (f(x-h) + f(x.+ h))/2)/2, где h — малое приращение координаты x; величины f(x. - h) и f(x. + h) определяются интерполяцией. Второй способ, в отличие от первого, в зонах монотонного решения, в которых нет мелкомасштабных осцилляций, никакого сглаживания не производит. При отсутствии явных физических доводов в пользу первого способа, первый этап можно исключить из процедуры сглаживания. Для описания упругих свойств материала принимается упрощенная форма закона Гука, полученная в предположении начальной изотропии свойств материала: о = XI(£-e p): I + 2ц(£-£ p), где параметры упругости Лямэ и предел текучести, определяющий границы упругого поведения материала, зависят от поврежденности следующим образом: л л -1000y -1000у _ _ -1000у X = Xoe Y, Ц = Ц0e Y, оp = ap0e Y. Индексом «0» помечены значения для неповрежденного материала. Локальным критерием разрушения является достижение максимальной главной деформацией положительного критического значения £d. Максимальная главная деформация при этом представляет собой деформацию растяжения. Условие разрушения имеет вид: 1 1/2 Fd = 2 max |_(£x +£у ) ±((£x -£у ) - 4£xy ) J M -£d ^ 0, где с помощью безразмерного масштабного множителя M =min(hx, hy) \ max[(xmax-xmin),(ymax-ymin)] учитывается корневая особенность, присущая концентрации деформаций у кончика трещины в упругом материале, что позволяет трактовать данный локальный критерий как приближенное представление обычного критерия разрушения механики хрупкого разрушения в терминах коэффициентов концентрации деформаций. Критерий разрушения с масштабным множителем улучшает или, правильнее сказать, обеспечивает сходимость численных значений интегральных критических нагрузок разрушения при измельчении сетки. Иначе получается, что чем мельче сетка, тем раньше наступает разрушение, поскольку на более мелкой сетке концентрация деформаций описывается все лучше и критические уровни деформации достигаются все раньше, при меньших значениях приложенной нагрузки. Конечно, критические нагрузки зависят от сеточного разрешения, но эта зависимость должна демонстрировать сходимость расчетных критических нагрузок к некоторому ненулевому предельному значению, что и обеспечивает масштабный множитель. Введение множителя не является окончательным решением проблемы сходимости расчетных критических нагрузок разрушения, но не исключено, что это шаг в сторону возможного ее решения. Может быть, кто-то придумает лучшую регуляризацию критерия разрушения. Важный особенностью принятого критерия разрушения является то, что он различает растяжение и сжатие, реагирует на сдвиг, так как сформулирован в главных осях, то есть критерий не так тривиален, как может показаться. Примеры расчета разрушения при сжатии образцов на основе этого критерия имеются в [10]. Как следует из расчетов, он работает лучше, нежели критерии для первых и вторых инвариантов тензоров деформаций или напряжений. Еще одна особенность критерия заключается в том, что он сформулирован в терминах коэффициентов концентрации полной деформации. Эта формулировка предпочтительнее других, так как полная деформация, в отличие от напряжений, упругих и пластических деформаций, не корректируется при интегрировании эволюционных определяющих соотношений, а однозначно определяется кинематикой процесса деформирования. В условиях отсутствия конкретных сведений о кинетике повреждаемости кинетическое уравнение для повреждаемости принимается в простейшей форме: ∂tγ=1000H(Fd) где H — функция Хевисайда. Большой коэффициент в правой части введен для обеспечения быстрой, но конечной скорости роста повреждаемости, при которой способность упругого сопротивления деформации при разрушении теряется за несколько временных шагов. Это позволяет рассматривать применяемую здесь математическую модель разрушения как регуляризованный и, одновременно, упрощенный вариант известной модели разрушения Маенчена–Сака [3], в которой напряженно-деформированное состояние при разрушении корректируется на одном временном шаге скачком. Мгновенная корректировка напряжений приводит при этом к появлению в численном решении нефизических осцилляций, которые, впрочем, можно устранить аккуратным нелинейным покоординатным сглаживанием.
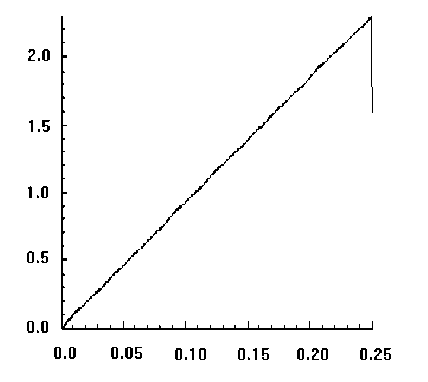
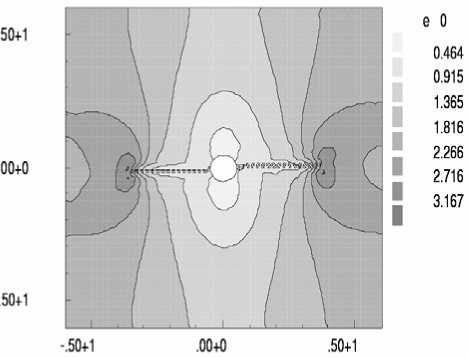
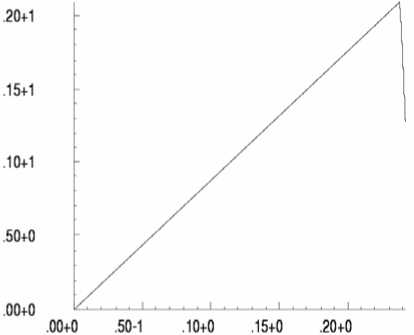
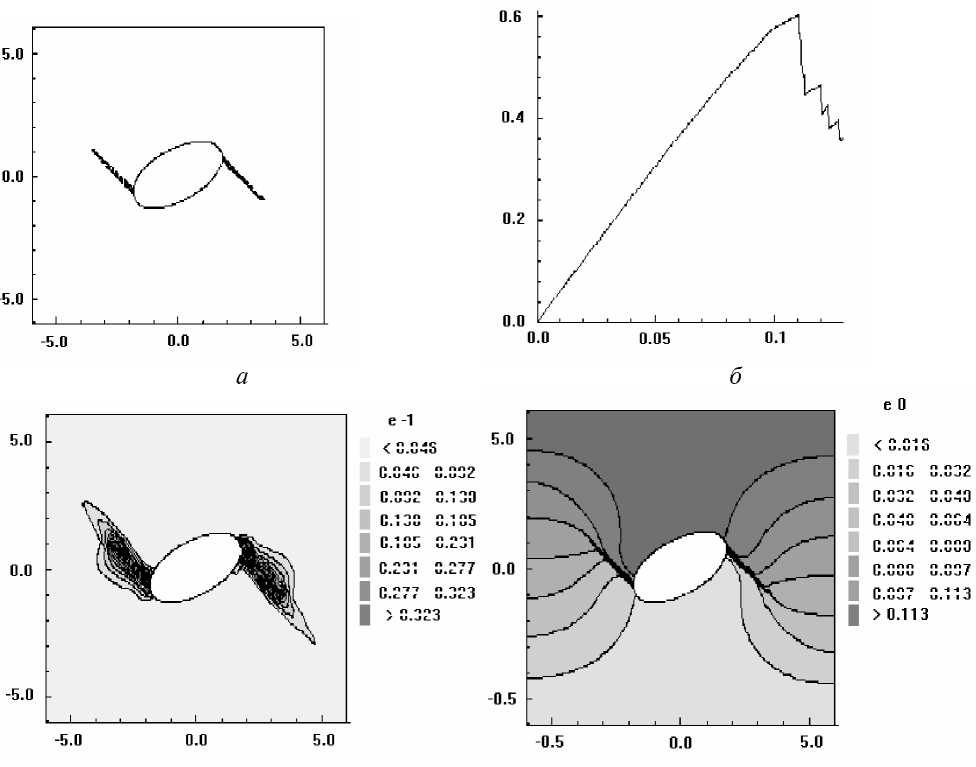
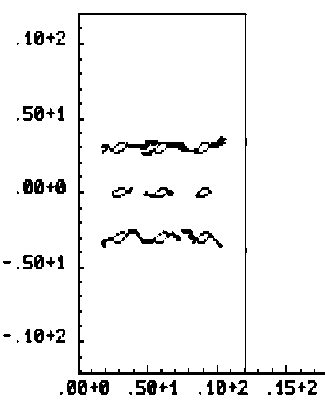
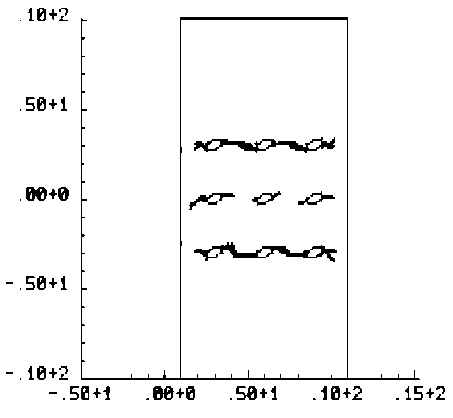
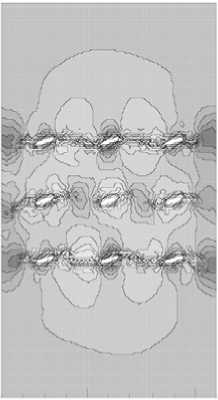
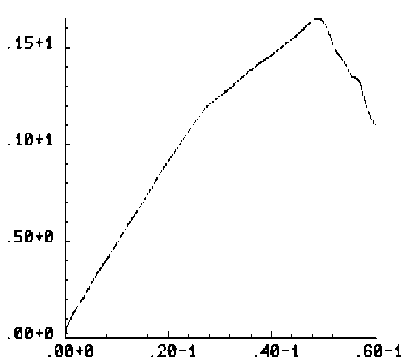
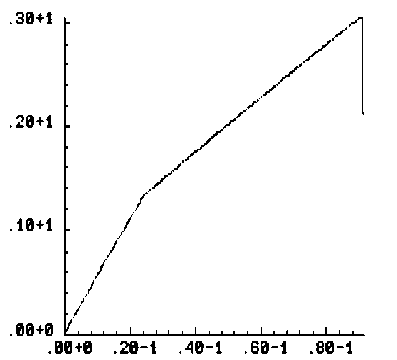
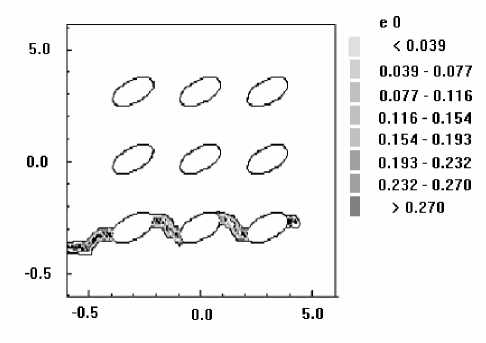
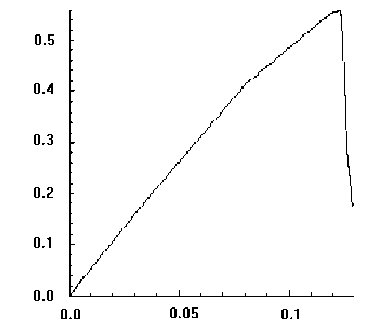
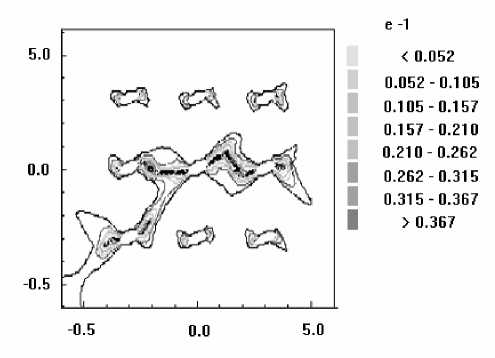
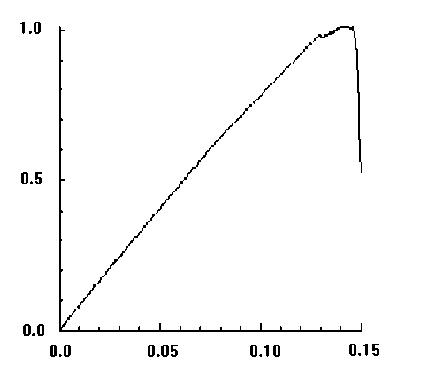
4. Результаты Рассматривается задача о развитии зон разрушения в растягиваемых плоских квадратных образцах с круглыми и эллиптическими вырезами, имитирующими макропоры или жесткие включения. Двумерная пространственная область решения принимается в виде квадрата в плоскости (x, y ), имеющего круглые или эллиптические вырезы, которые трактуются либо как макропоры, либо как жесткие включения. Сетка треугольных конечных элементов является обычной почти равномерной сеткой, сгенерированной автоматически, и показывать ее смысла нет. На вертикальных границах квадратной области решения горизонтальные смещения полагаются равными нулю. Нижняя граница имеет нулевые вертикальные смещения, Верхняя граница с малой скоростью, много меньшей скорости звука в материале, движется вверх, что отвечает квазистатическому растяжению рассматриваемого тела. Касательные напряжения на границах полагаются равными нулю. На поверхности макропор внешние силы отсутствуют. В случае жестких включений вырезы полагаются заполненными абсолютно жестким материалом, полностью сцепленным с материалом в области решения. При решении в области жестких включений также вводится сетка и величины модуля упругости и предела текучести задаются в 100 раз большими по сравнению с их значениями для материала образца. Во всех случаях рассчитанные диаграммы деформирования изображают зависимость осредненного по верхнему горизонтальному сечению напряжения стy от монотонно возрастающего заданного вертикального перемещения верхней границы Uy . В безразмерных переменных координаты в области решения принимают значения -6,0 < x< 6,0 и -6,0 < у < 6,0. Для других параметров полагается: диаметр круглой поры и круглого жесткого включения — 1,0; отношение полуосей эллиптических пор — 0,5; угол поворота — 30°; модуль Юнга — 100; коэффициент Пуассона — 0,2; скорость звука — 1,0; скорость движения верхней границы vy равноускоренно возрастает от нуля при t = 0 до величины 0,001 при t = 105. При расчетах по модели идеально упругопластического материала предел текучести равняется единице. Деформация разрушения составляет 0,02. Результаты решения задачи для упругого тела с одной круглой макропорой показаны на рисунке 1, где черные узкие зоны соответствуют развивающимся макротрещинам, интенсивность затемнения соответствует величине максимальной главной деформации (а); график (б) изображает рассчитанную диаграмму деформирования. Случай с одним жестким включением продемонстрирован на рисунке 2. Различие картин разрушения объясняется разным характером концентрации деформаций около поры и около жесткого включения (Рис. 3). В случае поры разрушение начинается от наиболее удаленных от центра поры точек по горизонтальному направлению x , а для жесткого включения разрушение раньше наступает в наиболее удаленных от центра включения точках по вертикальному направлению y . Решение для эллиптической поры, ориентированной под углом 30°, в упругопластическом материале показано на рисунке 4, где изображены зоны разрушения (а), рассчитанная диаграмма деформирования (б), распределение пластической работы и вертикального смещения. Отчетливо видны всплеск значений пластической работы в зоне разрушения и скачкообразное изменение перемещения. а б Рис. 1. Круглое жесткое включение в упругом материале: зоны разрушения и распределение максимальных главных деформаций (а); рассчитанная диаграмма деформирования (б) а б Рис. 2. Разрушение упругого материала при наличии круглой поры: зоны разрушения и распределение напряжения σy (а); рассчитанная диаграмма деформирования (б) .50+1 .00+0 -.50+1 -.50+1 .00+0 .50+1 е -2 0.034 0.049 0.063 0.078 0.093 0.108 0.123 50+1 .00+0 -50+1 -.50+1 .00+0 .50+1 е -2 0.018 0.035 0.053 0.070 0.088 0.105 0.123 а б Рис. 3. Максимальные главные деформации около поры (а) и жесткого включения (б) в упругом материале < 0.01Е < 0.046 0.016 - 0.032 П.046 - 0.092 П.П92 - 0.1 30 0.064 - 0.080 0.231 - 0.277 0.080 - 0.097 0.097 - 0.113 0.032 - 0.040 0.040 - 0.064 0.130-0.185 0.185 - 0.231 0.277 - 0.323 > 0.323 в г Рис. 4. Разрушение идеального упругопластического материала при наличии одной большой овальной поры: зоны разрушения (а); рассчитанная диаграмма деформирования (б); распределение пластической работы (в); вертикальное смещение (г) На рисунках 5–7 приводятся результаты для разрушения образцов из идеального упругопластического материала с множественными эллиптическими порами и жесткими включениями, повернутыми на угол 30°: зоны разрушения (Рис. 5); распределение среднего напряжения для образца с порами и с жесткими включениями (Рис. 6); соответствующие рассчитанные диаграммы растяжения (Рис. 7). На рисунке 6 наблюдается разгрузка около берегов «трещин» и концентрация напряжений около кончиков трещин. На рисунках 8 и 9 сравниваются зоны разрушения и рассчитанные диаграммы деформирования для идеально-упругопластических образцов с большими и маленькими эллиптическими порами. Результат очевиден: при равном количестве пор образец с мелкими порами более прочен. В параметрических расчетах исследовано влияние характеристик дискретизации. Как выяснилось, в зависимости от размера пространственно-временных шагов и от формы ячеек сетки локальная картина разрушений изменяется в деталях, однако интегральные характеристики процесса, которыми являются осредненные вдоль верхней границы диаграммы деформирования образца, меняются при этом незначительно. а б Рис. 5. Зоны разрушения образца с порами (а) и жесткими включениями (б) а б Рис. 6. Распределение среднего напряжения для образца с порами (а) и с жесткими включениями (б) (темный цвет отвечает большим значениям) а б Рис. 7. Расчетные диаграммы растяжения (осредненное по верхней границе напряжение σ yy – вертикальное перемещение верхней границы U y ) для образца с порами (а) и жесткими включениями (б) а б а Рис. 9. Разрушение идеально-упруго-пластического материала с группой маленьких овальных пор, ориентированных под углом 30° , при отсутствии горизонтальных смещений боковых границ: зоны разрушения (а); рассчитанная диаграмма деформирования (б) Рис. 8. Разрушение идеально-упруго-пластического материала с группой больших овальных пор, ориентированных под углом 30° , при отсутствии горизонтальных смещений боковых границ: зоны разрушения (а); рассчитанная диаграмма деформирования (б) б
5. Выводы Численные эксперименты с простейшим вариантом теории повреждаемости показали: • сходимость результатов численного решения может иметь место «в большом» для интегральных характеристик, таких как диаграмма «осредненное напряжение — осредненная деформация», при этом картины разрушения «в малом» могут сильно зависеть от параметров дискретизации; • формулировка локального критерия разрушения в терминах коэффициентов концентрации полной деформации с введением масштабного множителя позволяет обеспечить сходимость расчетных значений времени начала разрушения при измельчении пространственных и временных шагов; • для локализации разрушения в виде узких зон контактных разрывов («магистральных трещин») требуется быстрая потеря упругого сопротивления деформации при накоплении поврежденности, иначе зоны разрушения охватывают значительную часть области решения и локализация деформаций отсутствует; • необходима монотонизация решения для устранения мелкомасштабных осцилляций численных решений, иначе такие нефизические осцилляции могут порождать ложные зоны разрушения; • сохранение сопротивления разрушенного материала всестороннему сжатию требуется для предотвращения счетного выворачивания ячеек в зонах разрушения; • учет сил инерции независимо от скорости нагружения позволяет сохранять корректность начально-краевых задач при фрагментации; • контроль точности путем ограничения нормы приращений решения на шаге по времени необходим для обеспечения сходимости решений «в большом» даже при использовании безусловно устойчивых неявных схем. Работа выполнена при поддержке Российского фонда фундаментальных исследований (проекты № 08-01-91302-инд-а, № 06-01-00523) и Программ фундаментальных исследований ОЭММПУ РАН № 13 и 14.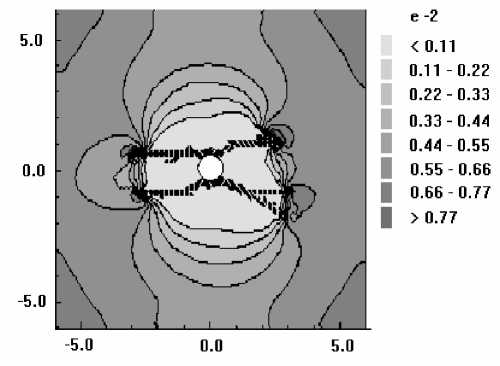



Список литературы Моделирование разрушения упругопластических тел
- Феодосьев В.И. Сопротивление материалов. -М.: МГТУ им. Баумана, 2007. -592с.
- Морозов Е.М., Никишков Г.П. Метод конечных элементов в механике разрушения. -М.: ЛКИ, 2008. -256с.
- Майнчен Дж., Сак С. Метод расчета «Тензор»//Вычислительные методы в гидродинамике. -М.: Мир, 1967. -С. 185-211.
- Фомин В.М., Гулидов А.И., Сапожников Г.А. и др. Высокоскоростное взаимодействие тел. -Новосибирск: Изд-во СО РАН, 1999. -600 с.
- Стефанов Ю.П. Некоторые особенности численного моделирования поведения упруго-хрупкопластичных материалов//Физ. мезомех. -2005. -Т. 8, № 3. -С. 129-142.
- Качанов Л. М. О времени до разрушения в условиях ползучести//Изв. АН СССР. ОТН. -1958. -№ 8. -С. 26-31.
- Работнов Ю.Н. Механизм длительного разрушения//Вопросы прочности материалов и конструкций. -М.: Изд-во АН СССР, 1959. -С. 5-7.
- Кондауров В.И., Фортов В.Е. Основы термодинамики конденсированной среды. -М.: МФТИ, 2002. -336с.
- Кондауров В.И., Мухамедиев Ш.А., Никитин Л.В., Рыжак Е.И. Механика разрушения горных пород. -М.: Наука, 1987. -218 с.
- Бураго Н.Г., Кукуджанов В.Н. Численное решение задач континуального разрушения: Препр./РАН. Ин-т проблем механики. -М., 2004. -С. 1-39 (URL: http://www.ipmnet.ru/~burago/papers/prepr03.pdf).
- Bazant Z.P. Reminiscences on four decades of struggle and progress in softening damage and size effect//Concrete J. -2002. -V. 40, N. 2, -P. 16-28.
- Jirasek M. Nonlocal models for damage and fracture: comparison of approaches//Int. J. Solids & Structures. -1998. -V. 35. -P. 4133-4145.
- Krajinovic D. Damage Mechanics. -Amsterdam: Elsevier Science, 1996. -774 p.
- Lemaitre J.A. Course on Damage Mechanics. -Berlin, Heidelberg, New York: Springer, 1996. -247p.
- Oliver J. Continuum modeling of strong discontinuities in solid mechanics using damage models//Comput. Mech. -1999. -V. 17. -P. 49-61.
- Voyiadjis G.Z., Kattan P.I. Advances in Damage Mechanics: Metals and Metal Matrix Composites. -Amsterdam: Elsevier, 1999. -556p.
- Кукуджанов В.Н. Микромеханическая модель разрушения неупругого материала и ее применение к исследованию локализации деформаций//Изв. РАН. МТТ. -1999. -№ 5. -С. 72-86.
- Barenblatt G.I. Damage accumulation: a non-local model//Structured Media-Trecop '01. In memory of professor Ekkehart Kröner. -Poznan: Publishing House of Poznan University of Technology, 2002. -P. 19-28.
- Бураго Н.Г., Кукуджанов В.Н. Численное решение упруго-пластических задач методом конечных элементов: Препр./АН СССР. Ин-т проблем механики. -М., 1988. -63с (URL: http://www.ipmnet.ru/~burago/papers/prep1988.pdf).


