Моделирование рецидива онкологического заболевания

Бюллетень науки и практики / Bulletin of Science and Practice

УДК 577.3.01(0.75)                                 

Новообразования молочной железы у женщин достигают 25% от всех онкологических заболеваний репродуктивной системы женщин, как в РФ [1], так и в большинстве стран Европы [2]. Характеризуются высокой смертностью — около 15% от всех смертей в структуре онкологических локализаций. Лечение осуществляется в большинстве случаев за счет внешнего вмешательства и химиотерапии, которая является ключевой в лечении онкологических заболеваний. На текущий момент достигнуты значительные успехи в снижении риска рецидива и смертности от рака молочной железы [3, 4]. Но вместе с этим в некоторых случаях действие препаратов на опухоль сопровождается появлением небольшого количества опухолевых клеток, на которые препараты не действуют. Новый пул клеток начинает увеличиваться в размерах, проявляя в последующем себя как рецидив заболевания.

Ткань молочной железы состоит из конусообразных долей, от которых проходят молочные протоки. Молочные протоки это полые нити со стенками из эпителиальной ткани. Рак молочной железы может возникнуть из клеток эпителиальной ткани протоков за счет случайных мутаций, вызванных внешними или внутренними факторами. У мутированной клетки нарушен механизм самоликвидации. В результате она и ее дочерние клетки начинает постоянно делиться, заполняя собой просвет протока. Питательные вещества опухолевые клетки, как и здоровые клетки эпителия, получают через кровеносные сосуды. Взаимодействие делящихся и нормальных клеток рассматривается как их конкуренция за функциональное пространство роста. При этом считается, что делящиеся клетки в условиях конкуренции оказывают ингибирующее влияние на нормальные клетки [5].

Одним из методов лечения является химиотерапия. Химиотерапия снижает риск рецидива и улучшает показатели выживаемости. Наиболее чувствителен этот метод лечения для опухолей с высокими стадиями заболевания, высоким риском рецидива. Терапия является ведущей в лечении пациентов с неоперабельным раком молочной железы. Рецидивы заболевания могут быть вызваны разными причинами. Одна из возможных причин - наличие в опухоли небольшого количества делящихся клеток, на которые препараты не действуют [6]. Пул таких клеток начнет увеличивается в размерах при уничтожении препаратами основного пула делящихся клеток. Возможна и мутация нескольких делящихся клеток под действием препарата, которые перестают реагировать на препараты.

Математическая модель

В математической модели опухоли молочной железы учитываются три типа клеток: нормальные, делящиеся и мутированные, которые возникают с началом действия препаратов из делящихся клеток [7]:

du

-= = ^u (1 -u -u2 -u3)-Drug(t)u, u2p = fau2 (1 - u - u2 - u3)- yu2 (u + u3), du -=- = ^3u3 (1 - в (U + u2)- u3) + 5 Drug (t) u, u   uu где 1 — количество делящихся клеток, 2 — нормальных клеток, 3 — клеток, не подверженных действию препаратов, ^, ^2 и ^3 — параметры, характеризующие скорости роста численности клеток.

В модели (1) предполагается, что оба типа делящихся клеток оказывают ингибирующее

yu-, (u. + u,)

.

влияние на нормальные клетки, уменьшая скорость их размножения на    3 1   37

Препараты действуют на делящиеся клетки, уничтожая их при непосредственном контакте со „ Drug (t) u скоростью 1 . Часть делящихся клеток матируют под действием препаратов, пополняя пул мутантов со скоростью 5Drug(t)u1 ( 0 < 5 <<1 ). Размер функционального пространства, в котором происходит рост всех типов клеток, принят за единицу.

Предполагается, что мутанты в конкуренции за функциональное пространство более интенсивно вытесняют нормальные клетки и материнские клетки. Это учитывается в третьем уравнении введением параметра

в ( < 1)

эффективности конкуренции.

u, = s u — 1

u ₃ = 0

За начальные условия принимаются: 1   , 2

То есть, предполагается, что в начальный момент времени в функциональном пространстве, заполненном нормальными клетками, появляется небольшое количество делящихся клеток. Четыре стадии заболевания определяются через значения функции u1 лежащих в диапазонах:

0 < u < 0.25. _n_ 0.25 <  u <  0.50. _ш_0.50 <  u <  0.75.

jy _ 0.75 <  u <  1

.

По данным Е. М. Аксель, Н. Н. Виноградова, А. Б. Гончарова, Е. П. Колпак, R. Dent, M. Trudeau, K. Pritchard большинство (около 70%) пациентов обращаются за медицинской поддержкой на третьей стадии заболевания [1, 7, 8]. С учетом этого принимается, что диагноз ставится на этих стадиях заболевания. Соответственно препараты в модели (1) начинают

0.50 <  u

вводиться в момент времени ^{t *} при условии, что

В отсутствие препаратов стационарной устойчивой точкой системы уравнений (1)

u 1 u^    0

является 1    ,  2    . То есть делящиеся клетки заполнят все функциональное пространство.

При выполнении неравенства ^ 1 <  Drug ⁽ t )

скорость роста численности делящихся

клеток станет отрицательной. То есть для ликвидации делящихся клеток необходимо, что бы скорость их уничтожения была выше, чем скорость их размножения. Вместе с этим при любом варианте введения препаратов в момент времени t* образуются клетки мутанты,

YUU которые начнет ингибировать нормальные клетки со скоростью 23, и уменьшать размер

1/ ^в . После

функционального пространства материнских и нормальных клеток на величину прекращения действия препаратов устойчивой неподвижной точкой системы уравнений (1)

становится

U — 0 u ₂ — 0 u ₃ — 1 , , .

Таким образом, в модели (1) в отсутствие препаратов ( Drug ⁽ t ) ^{_ 0} ) все функциональное пространство будет заполнено делящимися клетками, а возникновение клеток мутантов под действием препаратов приводит к заполнению функционального пространства дочерними делящимися клетками.

Имитационное моделирование

Параметры, входящие в систему уравнений (1), взяты из работ [6, 9]. Для случая параметров:

A = 0.04, a = 0.04, a = 0.04, у = 0.02, в = 1

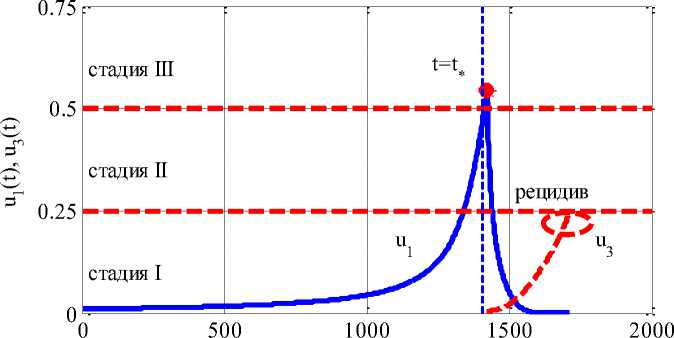
на Рисунке 1 приведена зависимость функции u ( t ) (сплошная линия) до введения препаратов на промежутке 0 <  t <  t„ и после введения препаратов в момент времени t = t* в количестве Drug = a • Рост мутантных клеток отмечен пунктирной линией.

Зона возникновения «рецидива» отмечена окружностью. Границы между стадиями отмечены горизонтальными пунктирными линиями.

t

Рисунок 1. Изменение функций u ( t ) и u ( t )

Модель (1) рассматривается как описание роста новообразования у конкретного «пациента». Параметры, входящие в эту систему уравнений, характеризуют биохимические характеристики новообразования [4, 9].

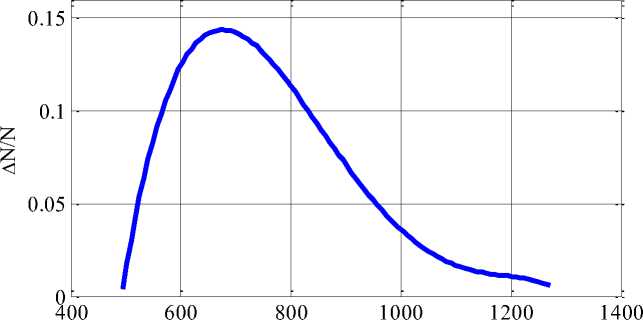
Предполагается, что эти параметры в когорте пациентов могут отличаться от некоторых «базовых» значений (2) не более, чем в три раза. В рамках этих предположений для выборки из N «пациентов», выбирая параметры модели случайным образом из заданных диапазонов, строится вероятность распределения момента начала «лечения» и вероятность распределения момента возникновения рецидива. На Рисунке 2 для случая N = 1000 пациентов приведено распределение вероятностей момента начала лечения, а на Рисунке 3 — распределение вероятностей момента возникновения рецидива после окончания «лечения».

Дни

Рисунок 2. Распределение вероятностей времени начала «лечения»

Момент время начала заболевания в клинической практике установить не удается. Тем не менее, в рамках модели (1) и кинетических параметров, приведенных в работе «”Естественная история” роста рака молочной железы», модель прогнозирует распределение вероятностей момента обращения за онкологической помощью близкое к нормальному распределению (Рисунок 2) [9].

Возникновение рецидива возможно в течении года после окончания лечения (Рисунок 3).

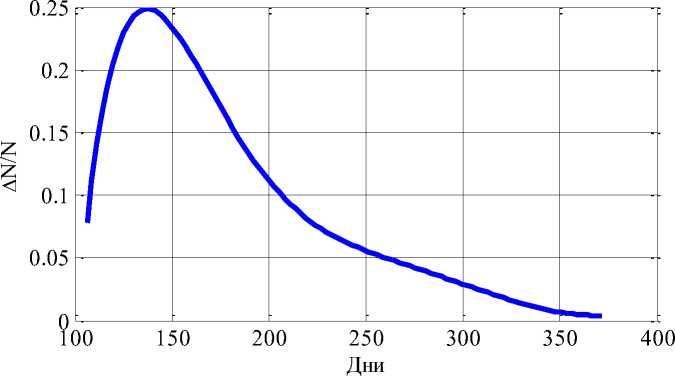
Рисунок 3. Распределение вероятностей времени проявления «рецидива»

По статистическим данным, приведенным в “Triple-negative breast cancer: Clinical features and patterns of recurrence”, рецидив проявлялся на временном промежутке до 4 лет [8].

Заключение

Разработанная модель прогнозирует наиболее вероятно наступление третьей стадии заболевания через 2-3 года после его возникновения (Рисунок 2), а проявление рецидива — через 4-7 месяцев после окончания лечения. Эти результаты согласуются с данными клинической практики [5, 8].

Полученные оценки могут быть использованы на стадии планирования онкологической поддержки населения.