Моделирование режима высокоскоростного фрезерования титанового сплава ВТ-9

деформирования мотивируется высокой интенсивностью деформаций, высокой локализацией очага пластической деформации (ОПД), а также возможностью бесступенчатой регулировки скорости деформирования v в широких пределах за счет использования металлорежущего оборудования, обеспечивающего внедрение и перемещения режущего клина в исследуемом материале.

Определяющие соотношения вида c s = CT s ( £ 2 , £ 2 ( v , 9 )) ,где CT s , £ 2 , £ 2 , 9 - соответственно интенсивность напряжений, интенсивность скоростей деформаций, температура в области деформации, можно получить теоретикоэкспериментальным методом, при котором силовые параметры находятся экспериментально, деформационные (средневзвешенная по объему ОПД интенсивность скорости деформации) определяются на основе полей кинематически допустимых скоростей течения (КДПС) v_i , например, методом верхнеграничной оценки. Для этого достаточно иметь достоверную картину пластического течения в ОПД, локализованного у кромки режущего клина, и вид исследуемой феноменологической модели упрочнения деформируемого материала с экспериментально определяемыми неизвестными коэффициентами.

Мощность резания в очаге пластической деформации объемом W, локализованного у режущей кромки, определяется зависимостью:

P = J ».-£2,9)£dw.

W

В свою очередь,

^£ 2 = ^£ 2 ^{( 9 (} v 0 ), v ), ^£ 2 = J ^£ 2 ^dt , t

где V0 - скорость движения деформирующего инструмента (в нашем случае режущего клина), vi - виртуальное кинематически допустимое поле скоростей (КДПС) в объеме W.

Произведение относительных величин ширины резания a_e и глубины резания определяют величину смещаемого (срезаемого) объема материала в единицу времени, поэтому минимум

j-участке ОПД для КДПС v , , е_{г evj} ( v , ) =

f б_г j ( v , ) dw

W j

W j

функционала

С—1

V a e a p )

соответствует минималь-

– средняя по локальному объему W _j интенсивность скорости деформаций на j –участке для КДПС v_i . Переменная p _j имеет физический смысл относительной мощности смещения (срезания) слоя металла при o s = 1 , рассеиваемой в единичном объеме

ной диссипации мощности, затрачиваемой на пластическую деформацию.

Поскольку действительная картина течения материала в ОПД априори не известна, то для практических целей поиска минимума min достаточно определить значения o s = o s ( s ₂, s₂.6 ) в характерных областях ОПД. Для этого условно разделим ОПД на N характерных областей, геометрия которых определяется положением условной плоскости сдвига, задаваемой коэффициентом усадки толщины срезаемой полосы А , и геометрией режущего клина. В этом случае (1) запишется как:

Wj для j – области ОПД. КОПД ap

(v f J o опд

– коэффи-

N

^P = Е f ° s ^{( S} 2j , ^S j , ⁶ j ^{) S}2j^d w .     (3)

j = 1 Wj

В каждой из этих N областей зададим v_i – виртуальное КДПС течения металла при реза^нии, v = v 0 • ( /_ond ) , , где ( f опд ) , ^- принятый ^закон изменения скорости деформирования, v ₀ -скорость резания. Согласно экстремальным принципам механики сплошной среды, если КДПС v_i приближается к действительному полю скоростей v , то для каждой пары фиксированных значений v ₀ , 6 пластический потенциал

[ P (v)1 ( a. a j

стремится к своему минимуму. В этом слу-

чае, в соответствии с экстремальными принципами механики сплошных сред и по теореме о наибольшем значении функции, действительная (измеряемая) мощность деформирования P ( v ) изм соотносится с теоретической P ( v ) _теор согласно зависимости:

изм

<

P^

N

1Е

a e j = 1

& 2max j ⁽ v i X j ] P j <

< os----КОПД(voLd)  v.^v >mn apae                   '

P j = /'2 j v i ⁾J— I a = const a p ^p

циент влияния формы ОПД.

Зависимость (4) выражает достаточное условие для феноменологического моделирования определяющих соотношений o s = o s ( s ₂, < &₂, 0 ) , исходя из определенных исходных данных:

• -    кинематически допустимого поля скоростей v_i ;

• -    принятого (с неизвестными коэффициента^ми) закона упрочнения ^o s (^ max ⁽ v o f ond ), ⁹) ;

• -    измеренной мощности деформирования P ( v ) изм .

Высокоскоростная обработка (ВСО) с точки зрения сопротивления пластическому деформированию характеризуется одновременным действием процессов вязкого упрочнения (вязкотеку-честь) и температурного разупрочнения. Ввиду того, что измерение температуры деформирования резанием в процессе фрезерования у вершины радиуса инструмента технически затруднительно по причине локализации области интенсивного деформирования в диапазоне 0,01…0,2 мм и перемещения очага пластической деформации (ОПД) со скоростью до 800 м/мин, результат измерения имеет большую погрешность и носит оценочный характер. Для оценки температуры резания целесообразно воспользоваться аналитическим методом, изложенным в работах [1, 2, 3].

В данной работе используется феноменологический подход к реологическим свойствам обрабатываемого материала, поэтому для конструирования принципиальной схемы модели воспользуемся корреляционным анализом экспериментальных данных.

Вид функциональных зависимостей f 1 ( v ) и f ₂ ( 0 ) можно задать, используя подходы, применяемые в механике сплошных сред, которые устанавливают определяющие соотношения между напряженным и деформированным состоянием в условиях динамического нагружения. Наиболее простой и часто применяемой моделью является эмпирическая модель Джонсона-Кука [4, 5]. Данная модель определяет следующее соотношение для эквивалентного напряжения o s :

^o s = [ ^o о ^{+ o} e ^s > n ^o ] I ^{1 +} b ^ln &2 ] [ 1 ^- 9 m ⁶ ] , (5)

где £ 2max j ⁽ vi) = ^max{ £₇ j ( vi )} — максимальное

значение интенсивности скорости деформации на

где e ₂ =---²— - относительная интенсивность

S 2|o, = o, о деформации,

£

£ 2 =------ - относительная интенсив-

£

²I ° S = ^as 0

ность скорости деформации,

о - о

О =--относительная темпера-

О - О la's =a о      пл тура, na , b, то - эмпирически определяемые коэффициенты, характеризующие свойства материала при высоких скоростях течения и температурах деформирования, as° = a° + ae - предел текучести при О = 1, £ 2 = 1, £ 2 = 1 и скорости деформирования VOas = as° .

О_пл — температура плавления.

При высоких скоростях резания, в силу локализации ОПД в малом объеме, приближенно полагать:

ционное упрочнение, форму и размеры ОПД.

В итоге по доказанной теме о достаточном условии для нахождения определяющих отношений из серии K экспериментов по деформированию резанием согласно которой a (£ ,, О ) ® ^V “ ™1 ¹ , если выполняется условие s 2V 2’                              ,

I P^{V )} изм ] к

( l , к |{ 1 , к } с {1,...., K },{ a_e , a p , S z } I =

= ^{{ a}e , ^ap , s z ^} к ^{,( V} ° ) l ^ ^{( V} ° ) к ) , мы получаем искомые зависимости:

^a s = ^a s 1⁽ £ >⁾ ^ ^a s2^{( £} 2^, °)

° s 2^{( £} 2^{, О} )

[ P ( V ) им 1

Г

1+a2 l

a

О-О „„ ) ³

О ° -О л J

Л

,(8)

’e ^£ 2 " ” = ^a e

^V ° I ^a s = ^a s 0 A

^£ 2

Зависимость (5) целесообразно представить в форме:

° s = ^a 1 ^£ 2 ) • ^a 2^{( £} 2 , ^О ) • (6) где a s 1 ( £ ₂) = a ° (1 + a ° £ ₂ " ° ) - закон деформационного упрочнения;

a_{s 2}( £ ₂, О ) = ( a ° + a 1 In £ ₂)(1 - a ₂ О^{а 3}) - закон изменения вязкопластических свойств;

a ° , a _a , n _a - коэффициенты, которые легко получить при статических испытаниях.

Модель Джонсона–Кука характеризует температурное разупрочнение деформируемого материала (закон 1 - a ₂ О ^{a 3} ), возникающее в ОПД при высоких скоростях резания одн о временно c вязкопластическим(закон a ° + a 1 ln £ ₂ ) и деформационным (закон 1 + a_a £ ₂ " ^a ) упрочнением.

Сравнивая представленную на рис. 3.[3, стр. 84] принципиальную схему реологических свойств обрабатываемого материала и феноменологическую модель определяющих соотношений Джонсона-Кука, можно предложить следующий вид зависимостей для функционалов f , ( V ) и f > ( V ) : f . ( V ) = ln ( V ) , f _;( О ) = О ^т . В этом случае модель реологических свойств вязкопластического материала, обрабатываемого деформированием резанием, примет вид:

где a s ( £ ₂) - закон деформационного упрочнения, получаемый при традиционных статических испытаниях на разрывной машине, выраженный, например, в форме (6);

При фрезеровании условно можно принять следующую схему распространения тепла, которая представляет собой процесс нагрева обрабатываемой пластины непрерывно движущимся линейным источником тепла Используя принцип наложения, можно найти распределение температур в случае непрерывно действующего источника теплоты путем интегрирования температурных полей от отдельных источников.

При расчетах температур в пластинах в ряде случаев, в особенности если пластины тонкие, необходимо учитывать теплоотдачу в окружающую среду. Процесс распространения теплоты в пластине с поверхностной теплоотдачей выражается уравнением (4.12), в которое введен сомно-„- bt житель e

.

эксп

= C a ° + a 1 ln

v

v mo

•    1+ a

a

Г ^ОО )

Множитель e - ^bt учитывает теплоотдачу в окружающее пространство, но не отражает того факта, что теплота отдается с поверхности пластины и температура по ее толщине неравномерна. Однако ввиду интенсивности процесса резания и с учетом того, что температура измеряется в точке, расположенной посередине ее толщины, этой неточностью можно пренебречь.

l О ° о 7

, (7)

ДВИЖЕНИЕ ЛИНЕЙНОГО ИСТОЧНИКА ТЕПЛА (ФРЕЗЫ) ВБЛИЗИ КРАЯ ПЛАСТИНЫ

где P_эксп – усилие деформирования резанием, полученное экспериментально для пар значений v , О ;

a ° , a 1 , a ₂, a ₃ - постоянные коэффициенты, характеризующие свойства материала;

С – коэффициент, учитывающий деформа-

Допустим, что источник теплоты перемещается на некотором расстоянии от края пластины уо (рис. 1). Считая границу I-I1адиабатической, создадим отражение теплоты от нее.

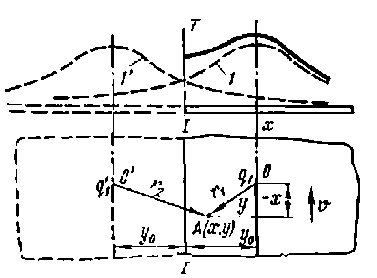
Рис. 1. Схема введения дополнительного движущегося источника q ^' для учета отражения теплоты от границы I-I1

Этого можно достигнуть, если предположить, что пластина бесконечна и в ней движутся одновременно с одинаковой скоростью два источника одинаковой мощности. Расстояние между действительным и фиктивным источниками равно 2y₀. Распределение температуры в некотором произвольном сечении от действительного q и фиктивного q ^' источников теплоты в бесконечной пластине показано на рис. 1 штриховыми линиями 1 и 1' соответственно.

Распределение температуры с учетом отражения теплоты от границы 1-1' представляет собой сумму температур от действительного и фиктивного источников теплоты и показано на рисунке сплошной линией.

Приращение температуры в некоторой точке А определяется следующей формулой:

vх ne = q e 2a 2пЛЗ

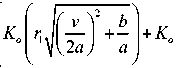
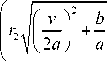
,(10)

где г = 7 x ² + y ² r = x ² + (2 y 0 - y )² .

АДАПТАЦИЯ ПОЛУЧЕННЫХ ЗАВИСИМОСТЕЙ ТЕПЛОПЕРЕДАЧИ ПРИМЕНИТЕЛЬНО К СХЕМЕ ЭКСПЕРИМЕНТА ПО ФРЕЗЕРОВАНИЮ

Выведенную зависимость приращения температуры от мощности движущегося линейного источника тепла необходимо адаптировать для условий фрезерования цилиндрической частью фрезы. Схема расположения точек контроля температуры приведена на рис. 2. Для вывода адаптированных зависимостей необходимо учитывать следующие моменты:

Точки контроля находятся на фиксированном расстоянии от оси инструмента, т.е. перемещаются относительно фрезеруемой пластины вместе с фрезой.

Точка резания перемещается с угловой скоростью вращения фрезы по кривой, определяемой величиной угла в (рис. 2).

В связи с первой особенностью принимается

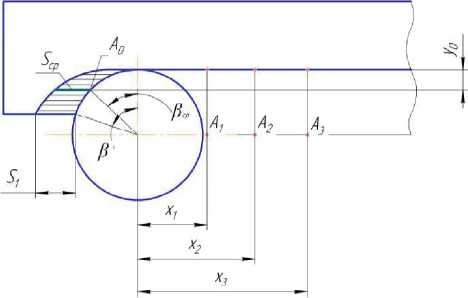
Рис. 2. Схема расположения точек измерения температуры (точки А1, А2, А3) при фрезеровании

закон скорости движения источника тепла (фрезы) v относительно точек измерения в соответствии с зависимостью (11)

v = ^kSмин = k— , (11) 60

где S_z , S_мин – соответственно подача на зуб и минутная подача, n - обороты шпинделя, z — число зубьев фрезы, k – экспериментально получаемый коэффициент, учитывающий особенности перемещения источника тепла в зоне резания.

В связи со второй особенностью только для задачи анализа тепловой мощности, выделяемой в процессе резания, примем, что тепловой источник находится на периферийной точке фрезы, соответствующей положению средней толщины срезаемого слоя (стружки) S_ср , определяемого углом в ср Вывод зависимости для расчета S ср приведен в приложении «Расчет средней (эффективной) толщины стружки».

Рассмотрим, согласно рис. 2, зависимости, описывающие основные геометрические размеры схемы измерения тепловой мощности:

S ср

^ Dz(sin(в) — ecos(в)) + (1 — в) ae L 4п                        2п в = arccos f1 — ^a^) В = -рв в

D^ср f ^, f_z

где a_e – ширина резания.

В соответствии с полученными выражениями для изменения температуры от линейного движущегося источника (4.18) с учетом закона движения (4.19) получим:

S zy       — к — мин х ne=^q^e 60*2a ЕK0(u)!=qAEK0 (u)!, (13) ?ьЛ( T )O где u = r

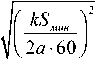
b

+ — a

A =

пЯ ( T ) 3

k мин e  60*2 a

параметр функции Бесселя K ₀ ( u ) ;

r = xx + y0 - расстояние от точки измере- ния температуры до точки резания;

a = 2TZL C p ( T ) P

– коэффициент температуропро- водности;

2 a                      1

b =-----, b0 = 10 3.....5-10 3 - - параметр теп- cppS                    c лоотдачи и его начальное приближение.

Таким образом, на основании (13) результирующая зависимость для расчета тепловой мощности резания принимает вид:

_      □ T q = А(k) •[Kо (u(k))] .           (14)

Коэффициент k , указанный как параметр, входящий в функцию Бесселя K ₀ ( u ( k ) ) и множитель А ( k ) в зависимости (14) означает, закон перемещения теплового источника резания в форме (11) получают экспериментально.

МЕТОДИКА РАСЧЕТА КОЭФФИЦИЕНТА k В ЗАКОНЕ ДВИЖЕНИЯ ТЕПЛОВОГО ИСТОЧНИКА В ЗОНЕ РЕЗАНИЯ

Очевидно, что если закон изменения температуры (13) задает распределение температуры около зоны резания с должной точностью, то тепловые мощности резания ( q ₁ ,..., q_n ) , рассчитанные по зависимости (14) и результатам измерения температуры в нескольких точках, удаленных на расстояния ( x ₁,..., x_n ) от источника тепла, должны стремиться к истинному значению q , если коэффициент k_теор будет стремиться к сво-

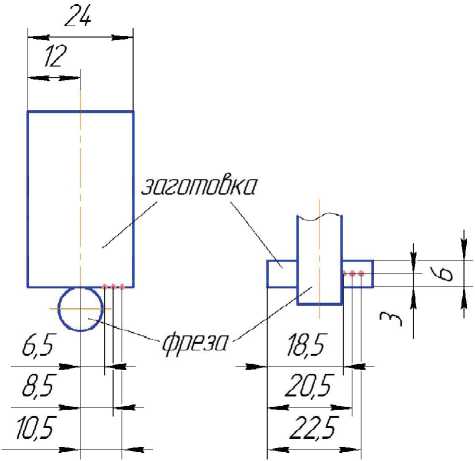
Рис. 3. Схема проведения измерения температуры ему действительному значению k .

Тогда справедлива зависимость, минимизирующая квадратичные отклонения:

Л

Е(q-q-«■) I ^k >min.

i,-=1)

Таким образом, коэффициент k , минимизирующий сумму квадратов отклонений, принимается действительным.

На практике с достаточной точностью можно рассмотреть 3 точки измерения (см. рис. 2). Коэффициент k по результатам анализа экспериментальных значений измеренной температуры, лежит в диапазоне 0,0001 <  k <  0,015.

Расстояние между точками измерения температуры, (рис. 2) определяется по зависимости:

x , = 5 .(1 + Sin( в ер ))

x 2 = x1 +□ x x3 = x1 + 2^ x

У 0 = a e - у ( cos⁽ Р ср ) - c^{0S( в )} )

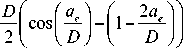
В проведенных экспериментах было принято значение шага □ х = 2 мм .

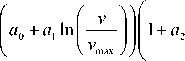
f ⁹ - ⁹ пл 7

1 9 0 - 9 пл )

Таким образом, в результате проведенных экспериментов по регистрации усилия деформирования резанием при различных скоростях перемещения режущего клина (зуба фрезы), был определен вид модели реологических свойств (8), требуемый для феноменологического моделирования определяющих соотношений из серии экспериментов по деформированию резанием.

ВЫЯВЛЕНИЕ И ВЫБОР ВХОДНЫХ И ВЫХОДНЫХ ПАРАМЕТРОВ

Входные параметры: Регистрация изменения составляющих усилия резания Fx, Fy, Fz в реальном времени с использованием динамометра Kistler модели 9257В установленного на стол станка ALZMETALL BAZ 15 CNC.

Измерение температуры проводилось с использованием пирометра IР140 в трех точках заготовки по схеме, приведенной на рис. 3.

Пирометр IР140 устанавливается на удалении 6,5 мм от зоны резания (18,5 мм от торца заготовки) рис. 4.

На компьютере, к которому подключен пирометр IР140, устанавливаем коэффициент излучения для материала ВТ-9 равный 50%.

Далее проводиться обработка материала со-

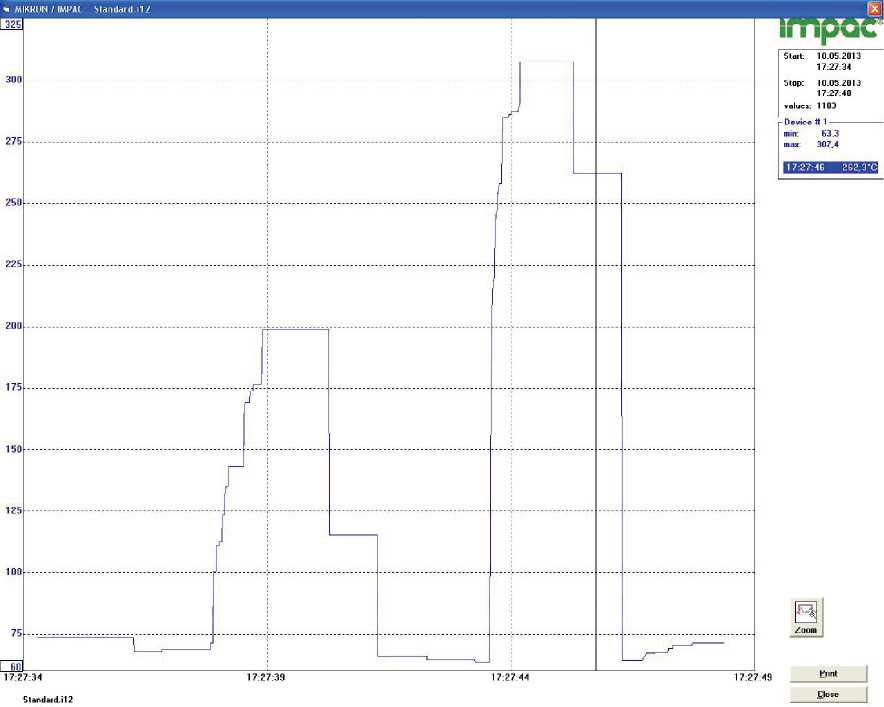
Рис. 4. График измерения температуры сплава ВТ9

Таблица 1. План проведения эксперимента для материала ВТ-9

№ опыта Sz, мм/зуб S, мин n, об/мин V резания ae, мм 1 0,15 1910 3183 100 0,3 2 0,1 1273 3183 100 0,3 3 0,15 1146 1910 60 0,3 4 0,1 764 1910 60 0,3 5 0,15 1910 3183 100 0,1 6 0,1 1273 3183 100 0,1 7 0,15 1146 1910 60 0,1 8 0,1 764 1910 60 0,1 гласно плану проведения эксперимента таб. 1, на экране компьютера строиться график измерения температуры рис. 4 и записывается текстовый документ со значениями температуры по времени проведения эксперимента.

На графике температуры (рис. 4) видно два температурных пика первый около 200°С это замер температуры калибровочного прохода, второй 307, 4°С экспериментальный. Калибровочный проход выполняется всегда на одних и тех же режимах резания (одинакова подача, скорость резания, глубина резания и т.д.). Калибровочный проход необходим для обеспечения однотипных условий для проведения эксперимента таких, как шероховатость поверхности, вылет заготовки и т.д.

После проведения замеров на всех режимах согласно плану проведения экспериментов, пи- рометр выставляется на следующую точку по схеме, приведенной на рис. 3 и проводится следующая серия экспериментов.

При измерении сил резания с помощью динамометрического стола Kistler были получены графические зависимости составляющих Fx, Fy, Fz силы резания от времени. На рис. 5 представлены данные по 8 каналам измерения и зависимости Fx, Fy, Fz для сплава ВТ-9 для опыта №1 (таб. 1).

Далее выбираются только зависимости составляющих Fx, Fy, Fz силы резания (рис. 6). Составляющие силы получились отрицательными, т.к. направление составляющих сил было противоположно положительным направления осей динамометрического стола. При дальнейших расчетах учитывались только значения сил, т.е. знак не учитывался.

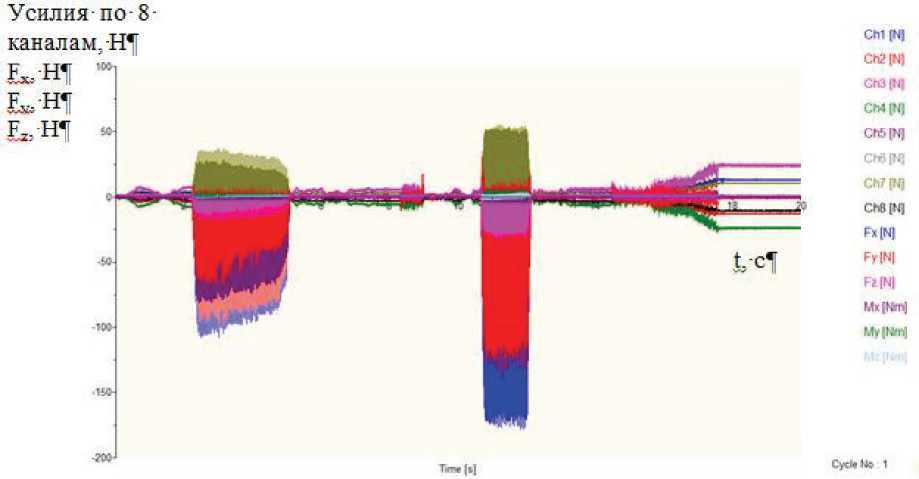
Рис. 5. Данные по 8 каналам измерения и зависимости Fx, Fy, Fz для сплава ВТ-9 для первого режима

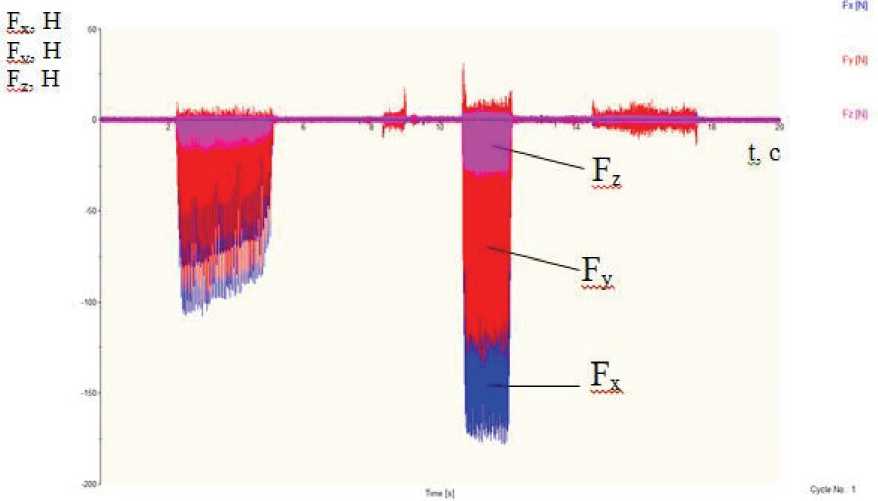
Рис. 6. Зависимости составляющих Fx, Fy, Fz силы резания

Затем с помощью программного обеспечения динамометрического стола программно определяется результирующая сила резания. Её значение записывается в канал 6 (Ch6). Зависимость результирующей силы резания от времени представлена на рис. 7.

На рис. 7 показана зависимость, на которой отражен предварительный проход (примерно со второй по пятую секунду записи), а также рабочий проход (примерно с десятой по двенадцатую секунду записи). Рабочий проход записан полностью. Из него с помощью увеличения масштаба рисунка необходимо выбрать часть зависимости для одного зуба (рис. 8), т.е. часть времени, в те- чение которого в контакте с заготовкой находится только один зуб фрезы. Желательно выбирать эту часть из середины прохода.

Такие же действия повторяются для каждого режима. В результате получается набор графиков зависимости результирующей силы резания от времени.

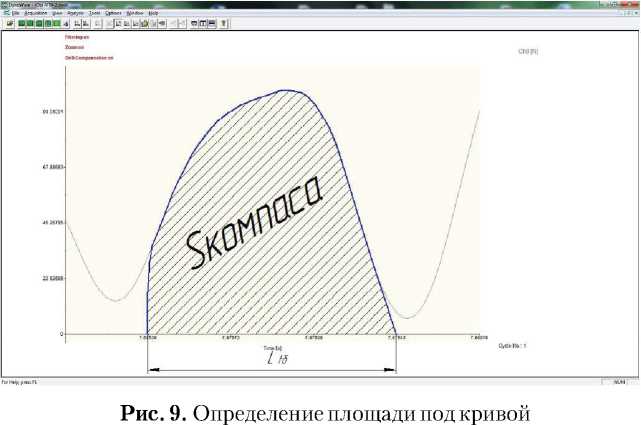
В результате эксперимента были получены графики распределения составляющих силы резания (рис. 8). Для обработки полученных данных необходимо определить масштаб по осям х, у. Строим сплайн, измеряем площадь кривой в программе KOMPAS – 3D Sкомпаса, [мм2].

Зная площадь можем определить действительное усилие резания, которое действует на зуб.

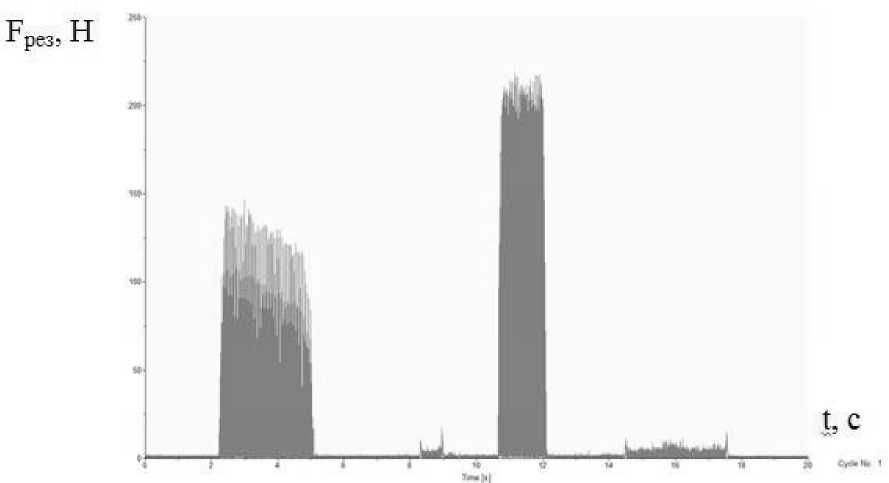
Рис. 7. Зависимость результирующей силы резания

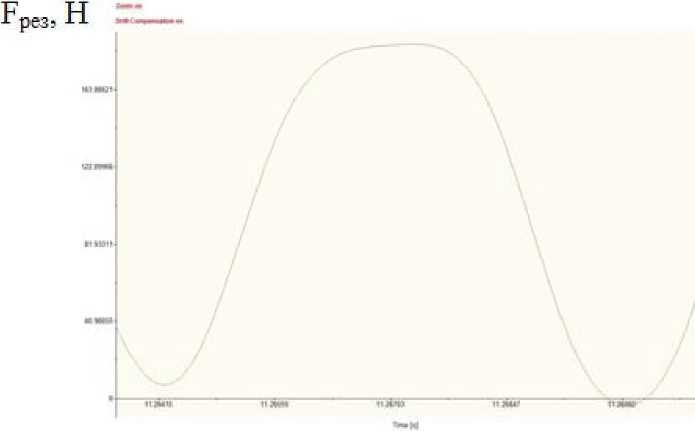
Рис. 8. Зависимость результирующей силы резания

РЕЗУЛЬТАТЫ РАСЧЕТА КОЭФФИЦИЕНТОВ МОДЕЛИ ДЛЯ ТИТАНОВОГО СПЛАВА ВТ9 НЕТЕРМООБРАБОТАННОГО

Таблица 2. Расчетные коэффициенты модели, степень достоверности – 81%

Модель:

p = I 0,0040 - 0,0002 In | — III 1 + 260,5047 1 ^{1393 9}

(                   ( 100 JJI              ( 1053

	Значения коэффициентов	Коэффициент Стьюдента, t	Критерий статистической значимости*, p
a0	0,0040	0,000228	0,999829
a1	-0,0002	-0,000228	0,999829
a2	260,5047	0,000229	0,999828
a3	0,1708	0,054762	0,958954
* Если критерий p >0,05, то коэффициент статистически значимый.

Таблица 3. Таблица корреляций коэффициентов модели

	a0	a1	a2	a3
a0	1,00000	-1,000000	-1,00000	0,999580
a1	-1,00000	1,000000	1,00000	-0,999585
a2	-1,00000	1,000000	1,00000	-0,999580
a3	0,99958	-0,999585	-0,99958	1,000000

BT9 нетермообработанный Корреляции параметров

Относ, скорость             оооо               о резания

Относ, температура

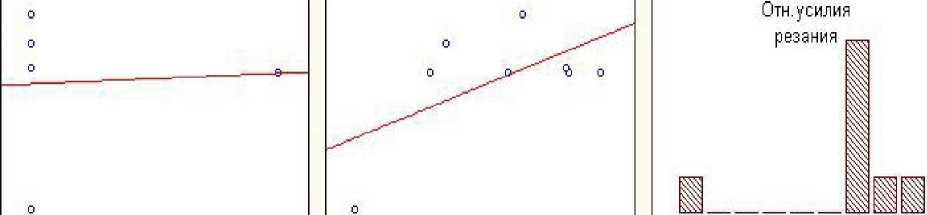
Рис. 10. График корреляций параметров

Титановый сплав ВТ9 нетермообработанный

2=((,003969)+(-.20е-3)Чод(х)П1+(260.505)Т(.17079))

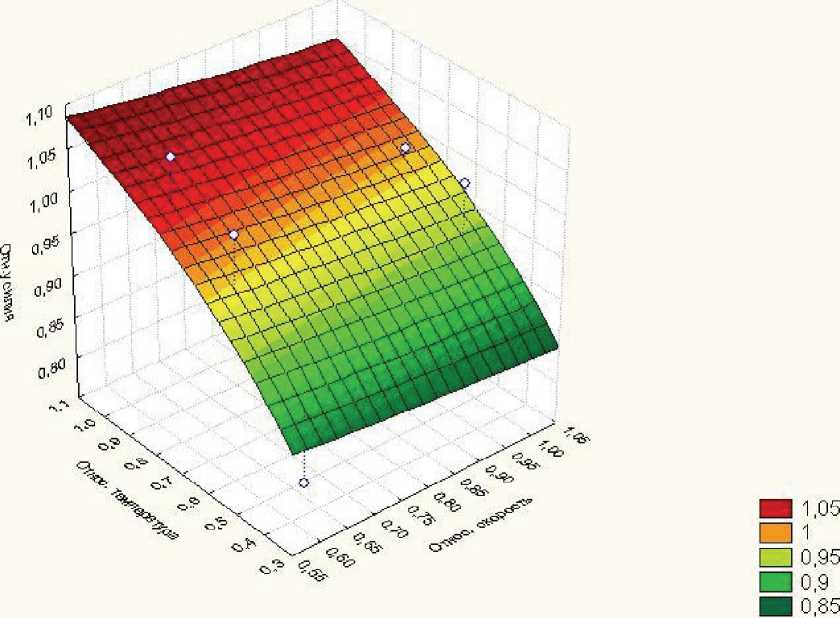
Рис. 11. Поверхность отклика (3-D график полученной модели реологических свойств для ВТ9)

РЕЗУЛЬТАТЫ РАСЧЕТА КОЭФФИЦИЕНТОВ МОДЕЛИ ДЛЯ ТИТАНОВОГО СПЛАВА ВТ9 ТЕРМООБРАБОТАННОГО

Таблица 4. Расчетные коэффициенты модели, степень достоверности – 98%

(          Л 393-Я

Модель: p = I 0,705751--0,042918lnI — 11 1 + 0,4163421 ¹³⁹³ ° (                     UOOJJI           ( 1053

	Значения коэффициентов	Коэффициент Стьюдента, t	Критерий статистической значимости*, p
a0	0,649470	0,000152	0,999888
a1	-0,039498	-0,000152	0,999888
a2	0,539049	0,000053	0,999961
a3	-0,004237	-0,000082	0,999940
* Если критерий p >0,05, то коэф		ициент статистически значимый.

Таблица. 5. Таблица корреляций коэффициентов модели

	a0	a1	a2	a3
a0	1,00000	-1,00000	-1,00000	-1,000000
a1	-1,00000	1,00000	1,00000	1,000000
a2	-1,00000	1,00000	1,00000	1,000000
a3	-1,00000	1,00000	1,00000	1,000000

ВТ9 термообработанный Корреляции параметров

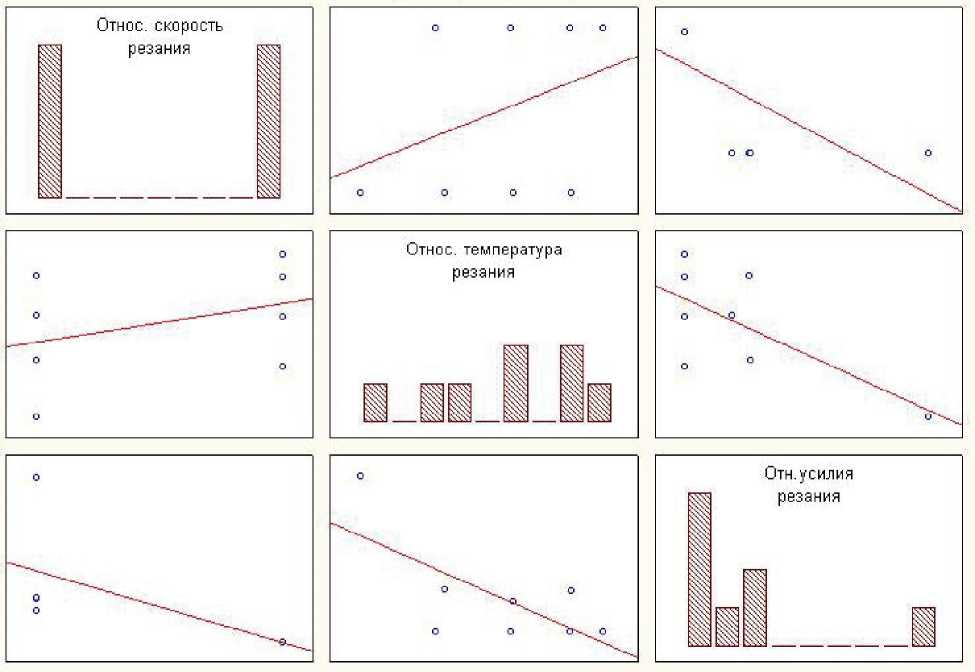
Рис. 12. График корреляций параметров

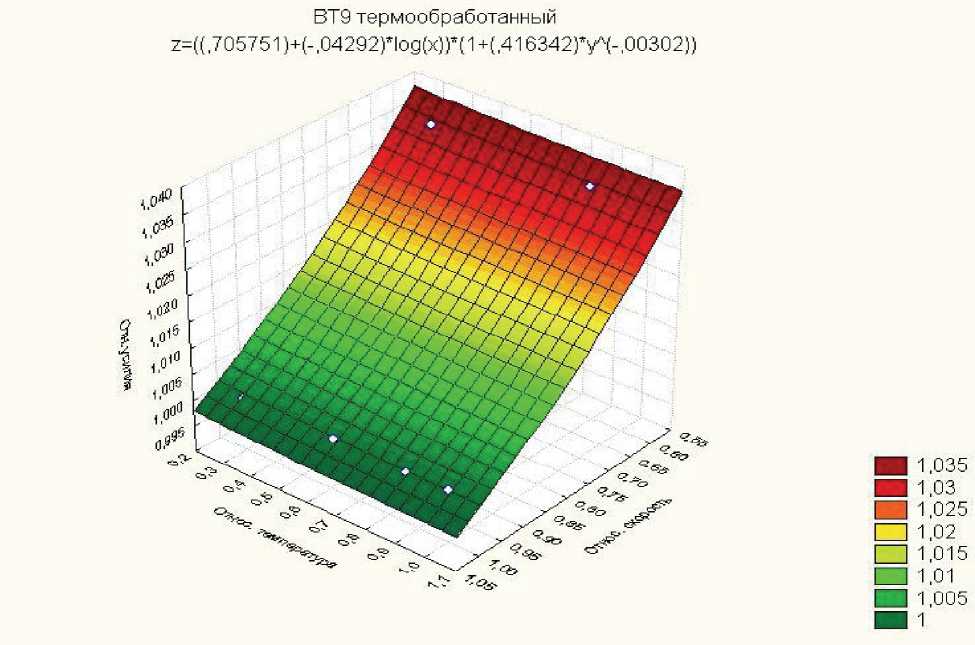
Рис. 13. Поверхность отклика

(3-D график полученной модели реологических свойств для ВТ9термообработанного)

ВЫВОДЫ

Разработана и апробирована методика определения реологических свойств материалов (определяющих соотношений, связывающих тепловое, напряженное и деформированное состояния) при обработке резанием в условиях максимально приближенным к реальным технологическим.

По результатам анализа проведенных экспериментов установлены определяющие соотношения (феноменологические модели реологических свойств) в форме модифицированного закона Джонсона-Кука, адаптированного к процессам резания:

ст = ст ( ^ ) I 0,0025 - 0,0002ln |     |1| 1 + 407,9664 1 139^{3 9}

s ² (               I 100 Д          I 1053

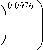
- 0,003022

– для нетермообработанного сплава ВТ9;

(                 С v » I          <1393-0

ст = ст(к,)I 0,705751-0,042918lnI — II 1 + 0,4163421 13------ s       27( ’             ’            llOOjJI      ’         ( 1053

– для термообработанного сплава ВТ9, где a ( s ₂) представляет собой закон деформационного упрочнения, определяемый по стандартной методике на разрывных машинах.

Установленные модели обладают высокой

степенью достоверности, которая составляет величину не менее 78%. Коэффициенты моделей ( a _o ,..., a ₃) являются статистически значимыми (высокий уровень критерия p).

Анализ реологических свойств ВТ9, подвергнутого обработкой резанием (фрезерованием) в состоянии поставки и в термообработанном состоянии по найденным феноменологическим моделям

свидетельствует о различии в реологических свойствах обрабатываемого материала в зависимости от состояния заготовки. Нетермообработанный сплав ВТ9 с увеличением интенсивности обработки и ростом температуры резания (относительная температура уменьшается) испытывает упрочнение в пределах 40% для рассматриваемых режимов обработки. Термообработанный сплав ВТ9 имеет стабильные реологические характеристики в этом же диапазоне. Упрочнение составляет не более 3%