Моделирование ромбоэдрической магнитострикции в сплавах Fe-Ga

Многофункциональные сплавы Fe _{100 - x} Ga x актуальны в технике в качестве магнитострикционных приводов, преобразователей энергии и датчиков микроэлектро-механических систем. Величина константы тетрагональной магнитострикции А оо1 в слабых магнитных полях достигает двух максимумов в диапазоне концентраций Ga 0 <  x < 35 ат.% [1—3]. Согласно экспериментальным данным наибольшие значения А ₀₀₁ обнаружены для x =19 ат.% ( ^ 180 х 10 ^{- 6} ) и x = 27 ат.% ( ^ 233 х 10 ^{- 6} ) и связаны с наличием в сплавах однородных структур A2 и D0 3 , в то время как уменьшение А оо1 в области около 25 ат.% Ga связано с сосуществованием нескольких фаз [3]. В то же время, величина константы ромбоэдрической магнитострикции Аш составляет порядка ~ 8, 5 х 10 ^{- 6} и ^ 40, 7 х 10 ^{- 6} в области пиков А оо1 [1,2] и является отрицательной в области x < 19 ат.% [2]. Вопросам экспериментального и теоретического изучения ромбоэдрической магнитострикции в сплавах Fe–Ga посвящено значительно меньшее количество работ, в отличие от тетрагональной магнитострикции А ₀₀₁ . Ресторфф ( Restorff ) и др. [2] провели исследование влияния изменения формы образца в магнитном поле на величину тетрагональной А оо1 и ромбоэдрической Аш магнитострикций, а также на константы магнитоупругого взаимодействия Ь 1 и b ₂ в сплавах Fe- X ( X = Al, Ga, Ge). Искажения формы образца снижают энергию размагничивания и оказываются существенными для низких и умеренных значений магнитострикции, а также для сплавов с высокой магнитострикцией и низкими модулями упругости. Авторы также пришли к выводу, что магнитострикция и магнитоупругое взаимодействие в этих сплавах обусловлены фазовым переходом ≪ беспорядок-порядок ≫ . С теоретической точки зрения влияние ближайшего окружения атомов Ga в структуре D0 3 на величину ромбоэдрической магнитострикции представлено в работе Жанга

( Zhang ) с соавторами [4]. Показано, что важную роль в определении знака λ ₁₁₁ играет симметрия и наличие несвязанных состояний вблизи уровня Ферми.

В данной работе проведено исследование зависимости величины ромбоэдрической магнитострикции сплавов Fe _{100 - x} Ga x (0 <  x <  28,125 ат.%) в структурных фазах A2, D0 ₃ и L1 ₂ в зависимости от концентрации атомов Ga методом теории функционала плотности.

1.    Теоретическая модель

Явление магнитострикции, связанное с изменением внешней формы магнетика при его намагничивании, оказывается существенным при рассмотрении доменной структуры и механизма намагничивания [5]. Относительная деформация образца δl/l ₀ (l ₀ длина образца в размагниченном состоянии) обычно очень мала в области малых магнитных полей (порядка 10 ^{- 5} ^ 10 ^{- 6} ) и возрастает с ростом напряженности магнитного поля, достигая состояния насыщения при некотором значении поля. В состоянии насыщения величину δl/l 0 обычно обозначают λ, и относительное изменение длины при переходе из размагниченного состояния в состояние насыщения составляет [5]:

δl               δl

"Т" | насыщения "7" | размагничивания • l0                     l0

Как и в случае магнитной анизотропии, представляющей собой явление преимущественной ориентации спонтанной намагниченности магнетика вдоль характерных для него кристаллографических осей, анизотропная магнитострикция определяется энергией спин-орбитального взаимодействия. В отсутствии магнитострикционной деформации кристалла расстояние между спинами фиксировано, и изменения внутренней энергии кристалла не происходит. При деформации образца изменяются длина и направление оси каждой спиновой пары в зависимости от направления вектора спонтанной намагниченности. Для кристаллов кубической сингонии магнитострикция может быть определена через относительное растяжение λ 111 (постоянная ромбоэдрической магнитострикции) и λ 001 (постоянная тетрагональной магнитострикции) вдоль направлений [111] и [001] соответственно, следующим образом [5]:

δl l0

³ _Л - 2 ^Л 001

i =1

+ ЗЛ 111 ^{( а} 1 ^а 2 ^в 1 ^в 2 + ^a 2 ^а 3 ^в 2 ^в 3 + ^а 1 ^а 3 ^в 1 ^в 3 ) ,

где α i и β i – направляющие косинусы намагниченности ( M ) и напряжения ( S ) относительно одной и той же кристаллографической оси. Направляющие косинусы намагниченности определяются как a 1 — sin 9 M cos ф _М , a ₂ — sin 9 M sin ^ M , a ₃ — cos 9 M , и напряжения в 1 — sin 9 s cos ^s , в 2 — sin 9s sin ^s , в ₃ — cos 9s .

Оценить ромбоэдрическую магнитострикцию λ ₁₁₁ можно в соответствии с выражением (1) путем определения δl/l 0 при повороте вектора намагниченности от оси [111] к оси [112] при напряжении, приложенном вдоль направления [111]. На рис. 1 показаны углы ϕ и θ , определяющие направления намагниченности и напряжения. Ромбоэдрическая магнитострикция выражается следующим соотношением:

λ 111

I (jl1

³ \l o

-

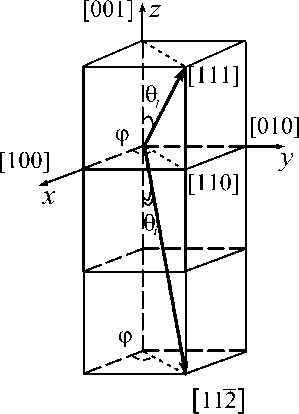
Рис. 1 . Углы ϕ и θ, определяющие направление вектора намагниченности вдоль осей [111] (^,0 j ) и [112] (^,9 i ). Напряжение параллельно оси [111]

δlδl

Величины |111 и l0

определяются в соответствии с соотношением

(2):

δl

Т 1 111 ^— l 0

^ 111    (Д — ^в 2 — ^в з ^— 1/V3, ^а 1 — ^а 2 — ^а з — 1/V³) ,

l 0 1 112 ^— - 2^ 111   ^1 ^{— в} 2 ^{— в} 3 ^{—    3 а} 1 ^{— а} 2 ^{— 1 /} / б, ^а 3 ^— — ^{2 /} / б^ .     (5)

Энергия магнитокристаллической анизотропии определяется как разность энергий с ориентацией спинов вдоль направлений [uvw ] и Е мин в соответствии с уравнением

E MKA    E [ uvw ]   ^Е мин ,

где E _мин – энергия системы с наиболее стабильной ориентацией спинов. Для определения Е МКА были вычислены энергии системы в направлениях [111] и [112] в зависимости от малых искажений ε при постоянном объеме. Постоянную ромбоэдрической магнитострикции λ ₁₁₁ в рамках теории функционала плотности непосредственно можно рассчитать с помощью следующего выражения [4]:

λ ₁₁₁

^{2 dE} MKA / ^ds _    b 2

3d ² Еполн /d² е ^— - 3d, полн.

— b ₂ —

² dE MKA

3V ds

Энергия кристаллической решетки при постоянном объеме может быть разложена в ряд по степеням малых деформаций ε

6           _{V 0} 6                  ₃

^Е полн. (V, ^{s ) Е} полн. (V C , °) + Vo ^ ^ ^ i ^s i + ^ ^ >   c ij ^S i ^S j + o ( ^S ) ,              ⁽⁹⁾

i =1               i,j =1

где c _ij – упругие константы, E _полн. (V ₀ , 0) – полная энергия недеформированной решетки объема V ₀ , ε _i и σ _i – тензоры деформации и напряжения соответственно.

Для расчета объемного модуля B = (Сц + 2С 12 )/3 и модулей С ‘ = (Сц — С 12 )/2 и C 44 были использованы изотропный, орторомбический и моноклинный тензоры деформации D _i (ε), представленные ниже, с шагом деформации 1% в диапазоне — 3% <  5 <  3%.

D 1 (ε) =

δ0

0δ

0   , D 2 (ε) =

δ

δ

— 5

0 0 δ 2		, D 3 (E) =	/	δ 2 1 — 5 2 δ	δ 0	0 0
1 — 5 2	)			0	0	0	/

Упругие константы были определены путем аппроксимации изменения полной энергии ∆E полиномами второго и четвертого порядков в соответствии со следующими уравнениями:

ДЕ = 9^ 5 2 + о ( 5 4 ) , (io)

ДЕ = 2V o C ‘ 5 2 + O (54) , (11)

ДЕ = 2V 0 C 44 5 ² + O ⁽ 5 ^{4 )} . (12)

Расчеты всех необходимых характеристик были выполнены в рамках теории функционала плотности, реализованной в программном пакете VASP [6, 7]. Обменно-корреляционное взаимодействие учитывалось в приближении обобщенного градиента в формулировке Пердью, Бурка и Эрнзерхофа ( Perdew, Burke and Ernzerhof ) [8]. Электрон-ионное взаимодействие описывалось методом проекционно-присоединенных волн ( projector-augmented wave, PAW ) [7] со следующей валентной конфигурацией атомов: Fe(3p ⁶ 3d ⁷ 4s ¹ ) и Ga(3d ¹⁰ 4s ² 4p ¹ ). Величина отсечения энергии плоских волн составляла 400 эВ. Для интегрирования по зоне Бриллюэна использовалась сетка Монхорст - Пака [9] размером 8 х 8 х 8 k-точек.

В недавней работе [10] было проведено исследование из первых принципов свойств пяти структурных состояний A2, DO 3 , B2, L1 2 и D0 19 сплавов Fe 1oo - x Ga x (x = 0 — 31, 25 ат.%). Полученная зависимость разности энергий кристаллических структур от концентрации атомов Ga показала, что наиболее устойчивыми являются фазы A2, D0 3 и L1 ₂ . Фаза A2 энергетически выгодна в области 0 <  x < 6, 25 ат.% в то время как состояние D0 3 устойчиво в диапазоне 6, 25 <  x < 21, 875 ат.% и фаза L1 ₂ обладает наименьшей энергией в области концентрации атомов Ga 21, 875 <  x < 31, 25 ат.%.

В данной работе рассмотрены следующие устойчивые структурные состояния: A2 (пространственная группа симметрии Im3m № 229, со структурой типа α-Fe) со случайно распределенными атомами Fe и Ga; D0 3 (пространственная группа симметрии F m3m № 225, со структурой типа BiF 3 ) с частично или полностью упорядоченными атомами Fe и Ga; L1 2 (пространственная группа симметрии Pm3m № 221, со структурой типа Cu ₃ Au) с частично или полностью упорядоченными атомами Fe и Ga.

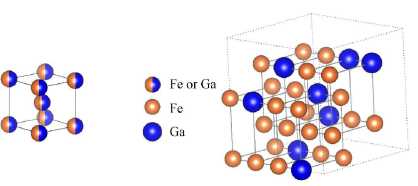
Моделирование было выполнено для 32-х атомных суперъячеек. Различные концентрационные конфигурации задавались путем замещения атомов одного сорта другим, при этом замена одного атома Fe/Ga соответствует изменению концентрации 3, 125 ат.%. Расчетные суперъячейки показаны на рис. 2.

a)

б)

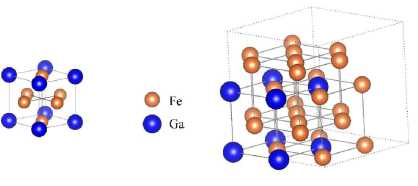
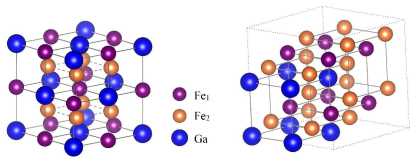
Рис. 2 . Расчетные 32-атомные суперячейки Fe ₂₄ Ga ₈ (соответствует сплаву Fe 7₅ Ga ₂₅ ) с кристаллическими структурами: а) A2, б) D0 ₃ и в) L1 ₂ и соответствующие им элементарные ячейки. Суперячейки получены транслированием элементарных ячеек вдоль кристаллографических осей в соответствии с формулами: 4 х 2 х 2 для фазы A2 и 2 х 2 х 2 для фаз D0 3 и L1 2

2.    Результаты моделирования

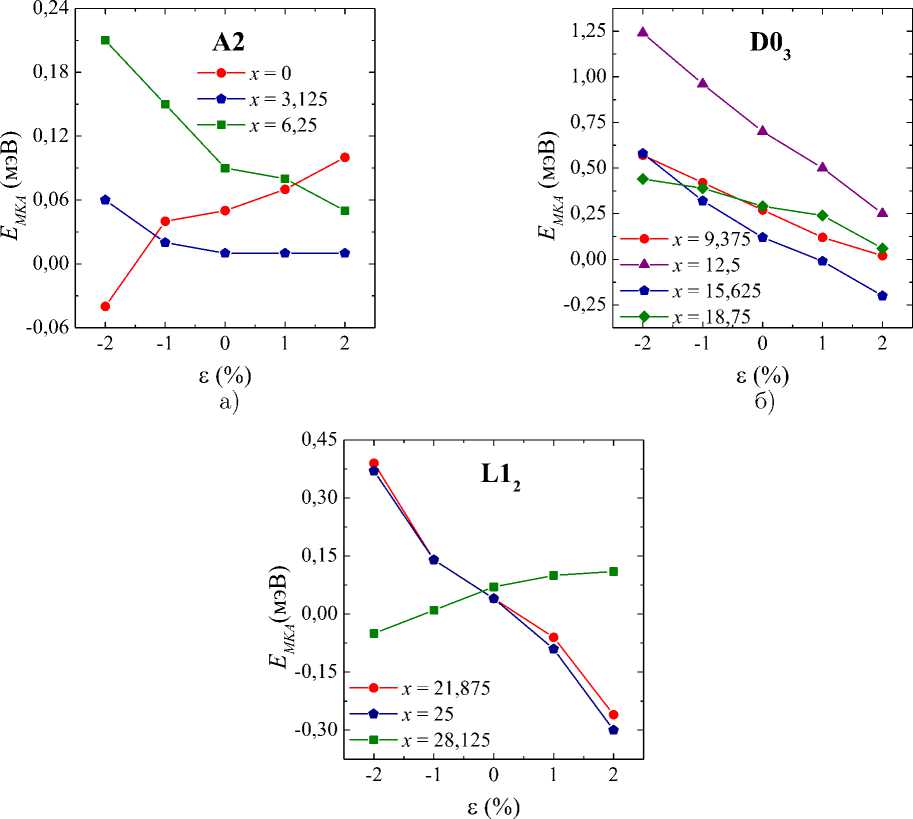
На рис. 3 представлены результаты исследования энергии магнитокристаллической анизотропии E _МКА кристаллических структур A2, D0 ₃ и L1 ₂ в зависимости от степени малых деформаций е в сплавах Fe _{100 - x} Ga x .

Видно, что в фазе A2 для чистого железа (α-Fe, объемно-центрированная кубическая решетка) наблюдается увеличение E _МКА с увеличением степени искажения, и происходит смена знака с отрицательного на положительный. В дальнейшем, с увеличением концентрации атомов Ga в кристаллических структурах вплоть до x = 28, 125 ат.% энергия магнитокристаллической анизотропии характеризуется отрицательным наклоном. В диапазоне концентраций 3,125 <  x <  12, 5 ат.% и при x = 18, 75 ат.% E _МКА для структур A2 и D0 ₃ является положительной. В области значений 21,875 <  x < 28,125 ат.% и при x = 15,625 ат.% Е МКА меняет знак с положительного на отрицательный при е >  1%.

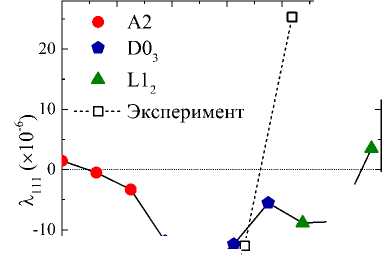
На рис. 4 а) приведены результаты расчетов ромбоэдрической магнитострикции А 111 в зависимости от концентрации атомов Ga. В диапазоне 0 < x <  12, 5 ат.% Аш уменьшается с увеличением содержания атомов Ga, достигая минимума при x = 12, 5 ат.%. При содержании Ga более 12, 5 ат.% в сплавах Fe _{100 - x} Ga x наблюдается увеличение ромбоэдрической магнитострикции в кристаллической структуре D0 ₃ . Для структуры L1 2 магнитострикция А 111 также увеличивается. В сплаве Fe ₇₁ , ₈₇₅ Ga ₂₈ , ₁₂₅ λ ₁₁₁ принимает положительное значение. Для сравнения на рис. 4 а) приведены экспериментальные значения λ ₁₁₁ , взятые из работы [2]. Можно отметить хорошее согласие полученных теоретических значений для фазы D0 ₃ с экспериментальными данными.

Полученные значения модуля упругости C ₄₄ , представленные на рисунке 4 б) хорошо согласуются с экспериментом при концентрации атомов Ga x >  12, 5 ат.%. Имеющиеся различия могут быть объяснены тем фактом, что вычисления выполнялись при T = 0 K, в то время как экспериментальные значения получены при комнатной

в)

Рис. 3 . Зависимость энергии магнитокристаллической анизотропии E МКА от степени малых деформаций ε в сплавах Fe _{100 - x} Ga _x для кристаллических структур: а) A2, б) D0 3 и в) L1 2

температуре. Кроме того, экспериментальные образцы могут быть многофазными, в то время как расчеты выполнены для случая однофазных монокристаллов.

Заключение

В настоящей работе проведено моделирование из первых принципов ромбоэдрической магнитострикции в сплавах Fe 100 - x Ga x (0 ≤ x ≤ 28, 125) для кристаллических структур A2, D0 3 и L1 2 . Показано, что зависимость E МКА (ε) имеет отрицательный наклон в диапазоне концентраций 3, 125 ≤ x ≤ 25 ат.% и достигает максимального значения в фазе D0 ₃ при x = 12, 5 ат.% и ε = - 2%. Рассчитанные значения модуля упругости имеют хорошее согласие с экспериментальными данными для сплавов с содержанием Ga x ≥ 12, 5 ат.%. Постоянная ромбоэдрической магнитострикции λ ₁₁₁ в диапазоне 3, 125 ≤ x ≤ 25 ат.% имеет отрицательные значения. При концентрации атомов Ga x = 12, 5 ат.% ромбоэдрическая магнитострикция достигает максимально-

А2 DO, ы2

□--- Эксперимент

О

•20

НО

о

10     15     20     25

Ga (х, ат.%)

А2

□--- Эксперимент

10     15     20     25

Ga (.V, ат.%)

a)

б)

Рис. 4. Зависимость а) ромбоэдрической магнитострикции и б) модуля упругости сплавов Fe100-xGax для кристаллических структур A2, D03 и L12 от концентрации атомов Ga го (по модулю) значения. В фазе L12 при x = 28,125 ат.% Лш становится положительной. В фазе D03 , полученные значения магнитострикции хорошо согласуются с экспериментальными данными

Работа проводилась при финансовой поддержке Российского научного фонда, гранты № 18-12-00283 (расчеты модулей упругости), № 17-72-20022 (расчеты ромбоэдрической магнитострикции).