Моделирование роста тонких пленок молибдата свинца PbMoO4 распылением ионными пучками

Тонкие пленки молибдата свинца PbMoO 4 , являясь акустооптическими материалами, широко применяются для создания изделий оптоэлектроники. Одним из перспективных методов выращивания слоев молибдата свинца можно назвать метод распыления ионными пучками [1].

В работе рассмотрены две методики синтеза молибдата свинца с использованием двух ионных пучков, осуществлено моделирование в зависимости от технологических параметров (расстояние мишень — подложка, размер подложки) с использованием математической программы MathCad. На основе полученных расчетов возможны рекомендации по определению оптимальных режимов роста тонких пленок.

Результаты и обсуждение

Процессы выращивания тонких слоев ионно-лучевыми методами возможны тремя способами: путем бомбардировки мишени пучком ионов инертного газа, бомбардировки пучком ионов химически активного газа и распылением с двумя ионными пучками.

В целом метод выращивания тонких пленок с использованием ионных пучков состоит из трех процессов: первый — распыление поверхности мишени ионным пучком; второй — перенос распыленных частиц к подложке путем преодоления расстояния от мишени к подложке; третий — непосредственно рост слоев на поверхности подложки. Каждый процесс весьма важен и требует пристального внимания.

В исследовании рассматривалась установка с двумя ионными пучками [1], в которой два ионных пучка независимо друг от друга распыляют две мишени. Рост тонких пленок молибдата свинца PbMoO4 в такой установке может быть осуществлен с использованием двух методик: первая методика предполагает независимую бомбардировку двух мишеней: из свинца Pb и из молибдена Mo; по второй методике независимо распыляются мишени из PbO и MoO3.

В первой методике путем независимого распыления двумя пучками ионов инертного газа (аргона Ar⁺) двух мишеней (Pb и Mo) молекулы свинца и молибдена достигают поверхности подложки, где и формируется пленка, состоящая из молекул свинца и молибдена. Молибден и свинец имеют различные коэффициенты распыления под действием ионных пучков аргона, которые были рассчитаны по теории Зигмунда [2; 3]. Поэтому для достижения соотношения 1:1 для каждой мишени подбирались разные энергии распыляющих ионов. Далее необходим дополнительный отжиг получившихся пленок на воздухе, в результате чего вначале происходит формирование простых оксидов PbO и MoO 3 , а затем осуществляется реакция образования стехиометрических пленок молибдата свинца PbMoO₄. Таким образом, рост слоев достигается в два этапа.

Во второй методике рост стехиометрических слоев молибдата свинца возможен в один этап согласно реакции: PbO + MoO 3 = PbMoO 4 . По данной методике путем независимого распыления двумя потоками ионов аргона Ar⁺ двух мишеней из PbO и MoO 3 свинец, молибден и кислород в виде молекул достигают поверхности подложки. Далее происходит поэтапное образование вначале простых оксидов PbO и MoO 3 , а затем реакция синтеза стехиометрических пленок молибдата свинца PbMoO 4 .

В настоящей работе была поставлена задача — сделать расчет процессов синтеза покрытий с использованием ионных пучков при параллельном расположении мишеней и подложки (рис. 1) при помощи математической программы MathCad. Были проведены расчеты толщины пленок в зависимости от геометрических характеристик эксперимента, а именно от расстояний мишень — подложка и размеров подложки. Учитывался также тот факт, что толщина слоев зависит от коэффициентов распыления мишеней.

Толщина покрытия определялась по формуле:

h = ^cosp cos<]) • t (1)

Частицы, выбитые ионным пучком с поверхности мишени, долетают до подложки и движутся по ее поверхности симметрично центру с расстоянием от центра l.

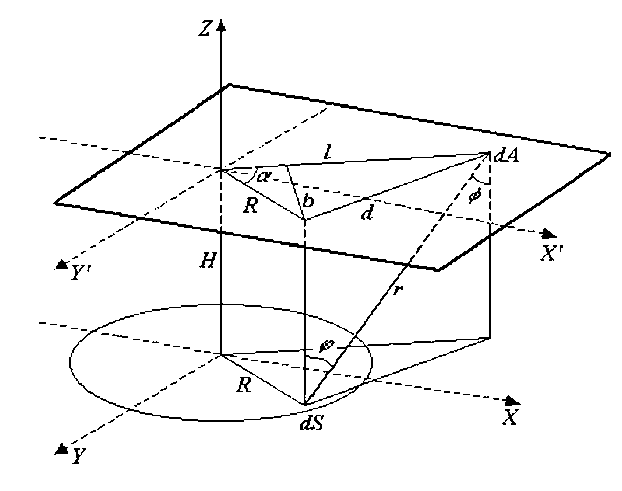
Рис. 1. Конструктивная схема расположения мишени и подложки в рабочей камере: H — расстояние между мишенью и подложкой, L — расстояние от упавшей частицы на подложку до центра подложки, R — радиус мишени, ϕ — угол падения пучка ионов на мишень, φ — угол падения частиц на подложку, r — расстояние от точки на мишени до точки на подложке, α — угол между l и R на поверхности подложки

Малый элемент поверхности мишени найден как:

dR*=R-da- dR(2)

Угол α определяется из отношения расстояния между мишенью и подложкой H и радиусом кольца r:

cos

Интегрируем по t, R, α:

h =    -—RdadRdt(4)

tRa^r2 r2

Расстояние r — это функция от L, R, d, H, α:

r = ^R2 + H2 + L2 — 2LR cos a,(5)

где l2+R2-2lRcosα =d2. Подставим выражение (5) в уравнение (4):

h = mD , , ; VT------Rddaddtdt(6)

tRa w(R²+L²+H²-2LR cos a)²

Интегрируя (6) по t, находим количество распыленного вещества. Скорость распыления не меняется и не зависит от радиуса кольца распыления:

h = — [L     ^^------RdadR(7)

я Ra u^(R+L2+H2-21R cos a)2v

В (7) производим замены переменных по углу, где b=H2+l2+R2, c=2lR, интегрируем и делаем обратную подстановку, получаем:

h2r h = Vt^R (R2+l2+H2)2-(2lR)2)3/2 d(8)

Скорость распыления равна:

где h — толщина распыленного материала; t — время процесса.

Скорость распыления при перпендикулярном падении ионов:

_v = j_u•s•мa ^•n_a^p ^,

где j и — плотность ионного тока, А/см²; S — коэффициент распыления, атом/ион;

М а — атомная масса атомов мишени, г/моль; е — заряд электрона; N а — число Авогадро; ρ — плотность материала, г/см³.

Распыление начинается при энергиях, больших пороговых (порядка 40 эВ).

По теории Зигмунда [2] коэффициент распыления можно найти по формуле:

S = ^-a- -^“_ . _^^

^²      (M_u+Ma)² 2E_cy6

где Ми — атомные массы ионов, г/моль; Ма — атомные массы атомов мишени, г/моль; Еи — энергия падающих ионов, эВ; Есуб — энергия сублимации атомов мишени, эВ; α — безразмерный параметр, зависящий от Мa/Ми.

Расчет толщин пленок

Для расчета в MatCad вводим H — расстояние от мишени до подложки и L — размер подложки. Определяем зависимость от этих переменных в виде матрицы. Переменная i принимает значения: i=0..15, где i — индекс переменной L.

Переменная j принимает значения: j=0..10, где j — индекс переменной H, т. е. Hj. Строка являлась функцией расстояния мишень — подложка, а столбец пока- зывал изменение толщины в зависимости от размера подложки.

Вначале производим расчеты для первой методики, когда два ионных пучка Ar+ распыляют мишени из Pb и Mo. Энергия распыляющих ионов 1 кэВ. Для наглядного изображения результаты вычислений представлены в виде графиков.

На рисунке 2 приведены результаты расчетов при распылении свинцовой мишени (Рb).

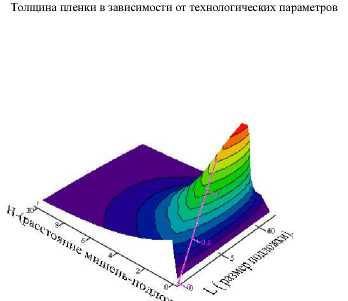
Толщина пленки в зависимости от технологических параметров

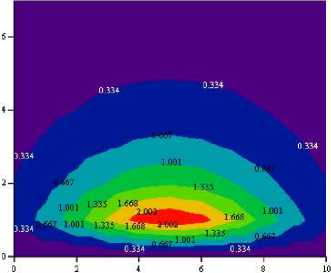
Рис. 2. Результаты расчета распыления свинцовой мишени Рb: а — график поверхности толщины пленки в зависимости от расстояния мишень-подложка и от размера подложки; б — график уровня толщины пленки в зависимости от расстояния мишень — подложка и от размера подложки

h

б

а) h

На рисунке 3 приведены результаты распыления молибденовой мишени (Мо).

б) h

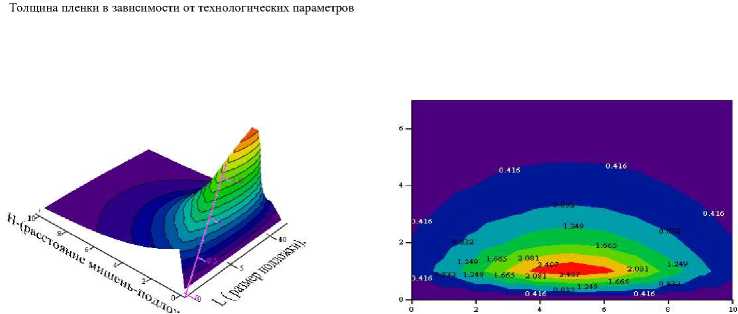
Рис. 3. Результаты расчета распыления молибденовой мишени Mo: а — график поверхности толщины пленки в зависимости от расстояния мишень — подложка и от размера подложки; б — график уровня толщины пленки в зависимости от расстояния мишень — подложка и от размера подложки

Далее были проведены расчеты для второй методики, когда два ионных пучка Ar⁺ распыляют мишени из PbO и MoO 3 . Энергия распыляющих ионов 1 кэВ. На рисунке 4 показаны результаты распыления мишени РbO.

а)

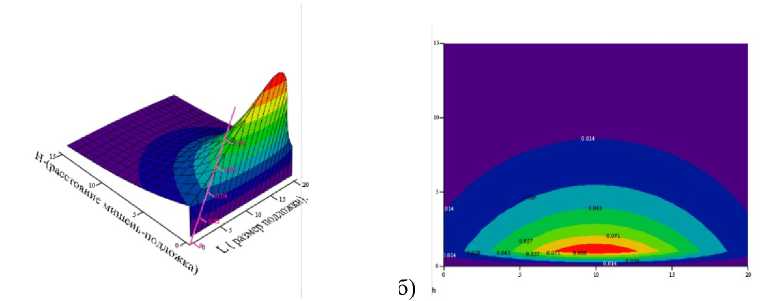
Рис. 4. Результаты расчета распыления свинцовой мишени РbO: а — график поверхности толщины пленки в зависимости от расстояния мишень — подложка и от размера подложки; б — график уровня толщины пленки в зависимости от расстояния мишень — подложка и от размера подложки

Анализ результатов расчетов показал, что применение первой методики приводит к тому, что при независимом распылении свинцовых (Pb) и молибденовых (Mo) мишеней (рис. 2а, 3а) оптимальными расстояниями между мишенью и подложкой являются расстояния H=2–3 см.

При использовании второй методики раздельное распыление мишеней из оксида свинца (PbO) и триоксида молибдена (MoO3) (рис. 4а, 5а) приводит к тому, что оптимальными расстояниями между мишенью и подложкой также являются расстояния H=2–3 см. По-видимому, это объясняется тем, что такие небольшие расстояния обеспечивают прямолинейные, без отклонения пути распыленных частиц. В результате они, не рассеиваясь, достигают поверхности подложек и активно участвуют в синтезе сложных соединений.

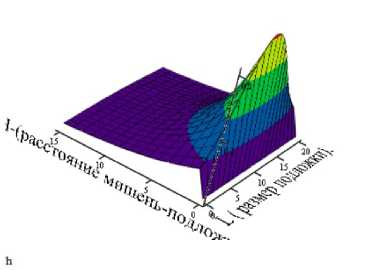
На рисунке 5 приведены результаты распыления мишени МоO 3 .

а)

б)

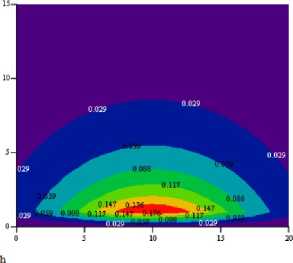
Рис. 5. Результаты расчета распыления свинцовой мишени MoO 3 : а — график поверхности толщины пленки в зависимости от расстояния мишень — подложка и от размера подложки; б — график уровня толщины пленки

в зависимости от расстояния мишень — подложка и от размера подложки

Что касается размеров подложек, то в случае использования первой методики при распылении свинцовых и молибденовых мишеней (рис. 2б, 3б) размеры подложек должны быть порядка L=4–5 см. Расчеты использования второй методики приводят к тому, что при распылении мишеней из оксида свинца и триоксида молибдена (рис. 4б, 5б) размеры подложек должны быть значительно больше: порядка 8–10 см. Возможно, это связано с тем, что при распылении оксидов распыленные частицы рассеиваются сильнее.

Поскольку скорость роста различных тонких пленок (Pb, Mo, PbO, MoO 3 ) прямо пропорциональна коэффициентам распыления соответствующих мишеней, следовательно, и энергиям распыляющих ионов, то толщины покрытий существенно различаются. За одинаковый промежуток времени наиболее быстрый рост наблюдается у пленок молибдена: h_max=2,5 отн. ед.; у пленок свинца несколько меньше (h max =2 отн. ед.). Значительно меньшие скорости роста наблюдаются у оксидных покрытий: у пленок оксида свинца h max =0,071 отн. ед.; у пленок триоксида молибдена h_max=0,176 отн. ед. По-видимому, это связано с более сложными процессами распыления оксидных мишеней по сравнению с однокомпонентными мишенями. Необходимо учитывать данные факторы при проведении реальных экспериментов, проводить внимательный анализ коэффициентов распыления, оценивать геометрические параметры в рабочей камере и другие особенности экспериментов.

Согласно первой методике на поверхности подложки проводится рост тонких пленок по реакции: Pb + Mo с последующим отжигом в атмосфере кислорода O2; с получением в конечном результате слоев молибдата свинца PbMoO4. Таким образом, данная методика предполагает рост слоев в два этапа и является более трудоемкой и длительной по времени по сравнению со второй методикой.

Согласно второй методике рост тонких пленок происходит в один этап: PbO + MoO3 = PbMoO4.

Выражаем надежду, что результаты наших расчетов помогут ученым в проведении реальных экспериментов и позволят определить наилучшие условия синтеза покрытий сложного состава.