Моделирование сейсмоакустического зондирования инородного слоя в безграничной среде

В настоящей работе представлены некоторые результаты исследования особенностей пространственного распределения амплитуды акустических, а также сейсмических SH-волновых полей на дистанциях, не превышающих нескольких десятков длин волн от виброисточника (переменный гармонический диполь), располагающегося вблизи неоднородности, отличающейся от окружающей среды по плотности или жесткости материала. Необходимость такого анализа связана с повышенным интересом к возможности дистанционного обнаружения в среде неоднородностей и прогноза их размеров и параметров при расположении приемо-излучающей системы на небольших удалениях от области, занятой зондируемой неоднородностью. В итоге подобные исследования направлены на решение так называемых «обратных» задач, то есть на проблему инверсии или реконструкции среды по данным вибросейсмического (акустического) зондирования. Несмотря на фундаментальные достижения в разработке их теоретической базы [1], остается еще недостаточно исследованной связь параметров структуры слоистой среды с конфигурацией полей излучения в окрестности виброисточника на масштабах в несколько десятков длин волн от него. Поэтому рассматривается частный случай, когда неоднородностью является инородный слой с плоскопараллельными границами, вблизи которого размещен источник излучения. В предшествующих публикациях [2–4] авторами статьи уже выдвигалось предположение, что на таких удалениях по особенностям конфигурации упруго-волнового поля можно прогнозировать наличие входящей в состав слоистой структуры среды неоднородности, предсказывать ее геометрические масштабы и возможные значения упругих параметров. В этой связи необходимо проанализировать возможность оценки дистанции источник – неоднородность, толщины (мощности) слоя, определения его акустических или упруго-волновых характеристик с использованием данных о характере или пространственной конфигурации поля на удалениях в несколько десятков длин волн (в особенности в условиях, близких к волновому резонансу). Это относится как к акустическим, так и к геофизическим задачам разведки залежей нефти.

В случае скалярной среды (жидкость или газ) для описания ее акустического поля достаточно одного скалярного потенциала, а источником колебаний является точечный осциллирующий диполь. В твердой среде поперечные SH-волны в двумерной постановке также представляются одной компонентой векторного потенциала, при этом гармонически осциллирующий силовой источник, равномерно распределенный вдоль бесконечной линии, параллельной границе слоя, имеет ту же ориентацию момента и излучает поперечные SH-волны, уходящие в направлениях, перпендикулярных этой линии.

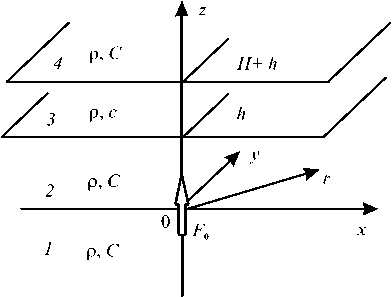
Рис. 1. Структура среды и расположение источника в акустической задаче

Далее по отдельности рассматриваются скалярная акустическая задача и аналогичная ей задача излучения поперечных SH-волн.

Геометрия расчетной области в первой задаче представлена на рисунке 1. Безграничное в трех измерениях пространство, заполненное жидкой или газообразной средой, характеризуемой параметрами р, С — плотностью и скоростью акустических волн, разделено слоем, безграничным по x, у направлениям и заключенным в пределах h < z < h + H по z . Внутри этого слоя среда отличается от окружающего пространства только скоростью звука c (с * C). Источник F0 z05(r)5(z)e-‘™t — точечный диполь, имеющий силу (момент) F0 и частоту осцилляций ю, представляющий собой возмущение в виде

5 -функции радиальной ( r ) и осевой ( z ) координат, ориентирован вдоль вертикальной оси ( z ⁰ — соответствующий орт) и расположен относительно одной из границ слоя на удалении h , вдвое превышающем толщину слоя H (такое количественное соотношение принимается как частный случай, удобный для выполнения расчетов).

На рисунке 1 все пространство разбито на четыре искусственно выделенные зоны (обозначены цифрами 1 , 2 , 3 , 4 ). Задача основывается на построении решения однородного волнового уравнения акустики:

А ф ^(1,2,4) - С.

д ² ф ⁽¹-²-⁴⁾ д t ²

= 0,

А ф ⁽³⁾ - -12- c

д ² Ф ⁽³⁾ = 0

д t ²         ’

причем действие источника учитывается не записью в правой части волнового уравнения (1), а в соответствующем граничном условии: со

Р ⁽²⁾ I z =0 ^- Р ⁽¹⁾ I z =0 = F 0 ^{5 (} r ) = С J J 0 ⁽ kr ) ^kdk ,                                  ⁽²⁾

^{2 п} 0

а также используется общеизвестная связь между потенциалом φ , акустическим давлением p и компонентой волновых смещений u_z :

p = рю ² ф,     u_z = V _z ф = д ф /д z .

В выделенных четырех расчетных областях поле акустических смещений может быть представлено интегральными выражениями (фактор e iюt далее всюду опускается):

_u t¹) = i^F 0

^z   4 прю ²

о I ii1- 1+

X

2 к ( ( К - к ) e^{i K H} + ( К + к ) e ) ' ( К-к ) ² ei"^H - ( К + к ) ² e "H ,

e ^{2 К h}

e i ^К J ₀ ( kr ) К kdk , z <  0;

о I

(2) ₌ J£» I ^{i к} z uz       .       2 J | e

4 прю ^J₀ I

-

e ^^{(2 h -} z ) 1 +

I

2 к ( ( К - к ) e^{i к H} + ( К + к ) e ^{- i K H} ) Y

( К-к ) ² e^{i к H} - ( К + к ) ² e ^{- i к H} ,

- J ₀ ( kr ) К kdk , h >  z >  0;

^о u (3) =___ iF 0 ^z    2 прю ^{2 i}

( К + к ) e ^- i ^{к ( H + h - z} ) + ( К - к ) e ”^{( H + h - z} )

( К-к ) ² e i

, i кH

- ( К + к ) ² e ^{- i к H}

e i ^{К h} J ₀ ( kr ) Кк kdk ,

U ? =

о

^{- iF} 0

прю ² J ( К-к ) ² ei"^H

e i К ( z - H )

- ( К + к ) ² e ^- i ^{к H}

J ₀ ( kr ) К ² к kdk , z >  H + h ,

где J0 (kr) — функция Бесселя нулевого порядка; r — радиальная координата; k — радиальная компонента волнового числа — переменная интегрирования; К = ^]ю2/С2 - k2 ; к = ^ю2/с2 - k2 .

Далее демонстрируются результаты численных расчетов поля только в 1 -й и 2 -й областях, в которых регистрируется поле, отраженное от неоднородности (рассеянное назад). На основе их анализа можно показать принципиальную возможность локации неоднородности, поскольку в пространственном распределении амплитуды этого поля проявляются некоторые характерные особенности, которые следует рассматривать как прогностические признаки присутствия слоя (неоднородности), имеющего скорость, отличную от скорости в окружающей среде. Результаты вычислений получены по формулам (4) путем их численного интегрирования. При графическом изображении найденного амплитудного распределения поля (Рис. 2) используется изометрическая проекция, в которой уровень поля представляется в виде рельефа, возвышающегося над плоскостью ( r , z ). В расчетах величина скачка скорости акустических волн (контраст) для сред внутри и вне слоя составляет с/С = 0,9 , а относительная удаленность источника от границы и мощность слоя, задаваемые в безразмерном виде, приняты следующими: to h/C = 11,1 п , to H/c = 5 п (слой имеет толщину H = 2,5 X , где X — длина акустической волны).

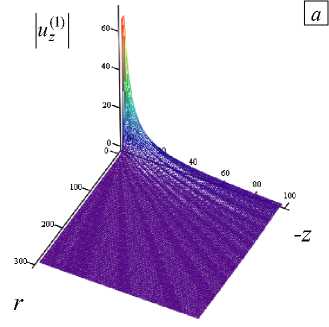
Рис. 2. Фрагменты картины распределения амплитуды поля uz над координатной плоскостью r - z : 1 -я область (а), 2-я область (б)

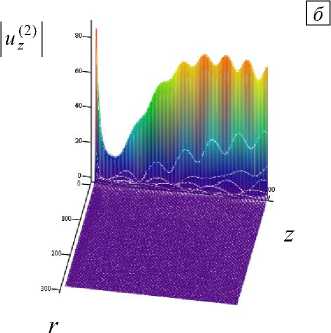
(в относительных единицах) – рельеф

Из рисунка 2, а видно, как резко спадает уровень поля при удалении от источника в направлении, противоположном неоднородности, и в пространственном распределении амплитуды имеют место веерные осцилляции. На рисунке 2, б по оси z применяется стократно увеличенный по сравнению с рисунком 2, а масштаб, что позволяет детально рассмотреть присутствие характерных вариаций амплитуды с ростом z в промежутке источник – ближняя к нему граница слоя. Данные вариации свидетельствуют о принципиальной возможности обнаружения неоднородности и локализации ее границ с использованием содержащейся в них информации. Выявленный факт подтверждается и при обратном соотношении скоростей с/С >  1, меняющем в картине поля заметно только его количественные амплитудные значения. К сказанному следует добавить, что осцилляции и спад уровня характеризуют также и поле, прошедшее внутрь самого слоя.

Аналогично решается задача нахождения характеристик акустического поля дипольного гармонического источника, которое является рассеянным назад и прошедшим сквозь инородный слой в безграничную однородную среду при различии свойств слоя и среды только по плотности. Область решения имеет ту же геометрию структуры слой – среда (Рис. 1) и то же расположение источника относительно границ как и в предыдущем случае. Здесь h — дистанция между источником и лицевой границей неоднородности, то есть плоскостью с координатой z = h , H — толщина (мощность) слоя. В предположении, что р 1 — плотность среды в окружающем пространстве, р ₂ — плотность среды в слое и при этом всюду одинаковая скорость звука C , нетрудно получить следующие выражения для акустического смещения, например, в отраженном ( u_z ⁽¹⁾ ) и прошедшем сквозь слой ( u_z ⁽⁴⁾ ) акустическом поле:

-IF Г u =TiM e

4 nP 1 to 0

, i 2К h

- 1 -

2 1 cos( K H ) - i ^ sin( K H )

I              P 2

2 cos( K H ) - г I   + ^{P 1} I sin( K H )

kP 1    P 2 /

e к ( h + н )

e - ^{i K z} J ₀( kr ) K kdk ,

u^ =

iF r                  e^{i K} ( z - ^H )

-2- [-------------т--------г--------- J ₀ ( kr ) K kdk .

^{2 np} 1 ^{to 0} 2cos( K H ) - г |^P 2 + ^Pl| sin( K H )

V^p 1 ^p 2 /

По формулам (5) вычислены структуры рассеянного назад и прошедшего сквозь слой акустического поля при разных величинах скачка плотности в слое и в окружающем пространстве: р2 /р1 > 1, р2/р1 < 1. Анализ структур позволил установить, что в окрестности источника, вследствие эффектов отражения от границ, возникает пространственная конфигурация акустического поля, качественно близкая к рассмотренной выше конфигурации при наличии скачка скорости звука в материале неоднородности относительно скорости звука в окружающей среде. Вместе с тем, при одинаковых контрастах скорости и плотности их материалов количественные значения амплитуды рассеянного поля в первом случае преобладают. Вследствие качественной близости конфигурации полей при обоих контрастах графические иллюстрации для поля со скачком по плотности в тексте не представлены.

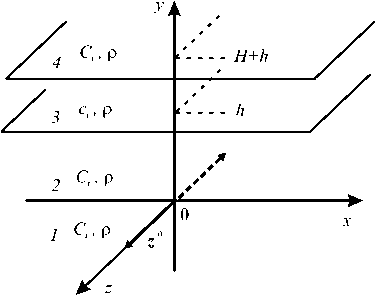
Рис. 3. Взаимное расположение источника и слоя, рассеивающего сдвиговые SH-волны

Геометрия расчетной области для задачи рассеяния поперечных SH-волн представлена на рисунке 3. Виброисточник Z 0 z08( x )8( у) e - i ™ t — «сила, осциллирующая с частотой ю», в силу двумерности приближения, используемого при анализе, равномерно распределен вдоль оси z (вектор силы параллелен орту z0, имеет амплитуду Z0, а фактор e-iюt, как и ранее, всюду опускается). В плоскости (x, y), которая пересекает фронты SH-волн, этот источник является ненаправленным. Как и ранее, слой занимает область пространства -да < x <да, к < у < к + H, -да < z < да. Окружающая среда характеризуется скоростью волн сдвига Ct и отличается от аналогичного значения ct внутри слоя;   обе среды имеют одинаковую по величине плотность р .

В предшествующих публикациях [2–4] авторами продемонстрировано, что для описания смещений uz у SH-волн сдвига в двумерную постановку задачи достаточно ввести одну компоненту векторного потенциала v x, которая должна удовлетворять однородному волновому уравнению:

Ау Х**²’⁴’

1 д Х Х¹’²’⁴’

Ct²     д t ²

= 0,

А^ Х³’

X д Х Х³⁾ c_t ²   д t ²

= 0.

При этом аналогично задаче с дипольным источником в скалярной среде все пространство разбивается на четыре специально выделенные области (Рис. 3), в каждой из которых колебательные смещения u_z и значимые в исследуемой волне напряжения ст выражаются через v _Х с помощью дифференциальных операций:

u ^⁴ = -dv X ¹-⁴’/д у ,

ст^² * ⁴ ) = р с ² д X²-⁴’ /д У ,      ст⁴’ = р С 2 д X’ /д У .

Действие источника, как и ранее, из граничных условий (при у = 0):

учитывается не в уравнении (6), а входит в описание одного

^СТ^’| у =0 ^-СТ”| у =0 = Z о8 ^{( Х} ).

Результирующие выражения, позволяющие вычислить волновые смещения, имеют вид:

u

(1) =

z

^{- iZ} 0

4 пр Ct²

да

(

-да

1 +

c t ^K t

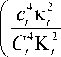
- 1 I sin( K t H )

e

,^- i ^K , H

c 2 K,

e ^{2 K} t h

-

-

e ^K , H

e ^- i ^к , у + ikx

К t

dk ,

2 i

I c t ^K t

I c k 2

- 1 l sin( K H ) e"^ж ■ ⁽ y ^{— 2} h ⁾

A

u

(3) =

z

^— iZ 0 2 np Ct²

J

u

(4) z

— iZ о c t np Ct⁴

c t ^{2 K} t

e

,- i ^K , ^h

c ² K

A

-

-

e^{1 K} , ^H

ikx e dk

K t

c^ + 1 ] e" • ⁽ y ^{— H — h} )

c t ^K t      L— i K t ( y — H—h )

¹ l ^e

e K t h + ikx

Г c ^{2 K} t

I C 2 K_t

Xх t

X

J

—i k, H

+ 1 l e '

c ² K ,

—

C_t ²K _t

—

1 l e^{i K} - ^H

K t

dk ,

k e i ^K t ⁽ у ^{— H ) + ikx}

—X

K 2

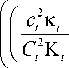
I     — i k, H

+ 1 l e '

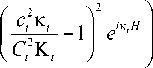
dk .

где K _t =д/ю ²/ C_t ² — k ², к _t =^/to ²/ c_t ² — k ² , C_t , c_t — скорость волн сдвига в окружающей среде и внутри слоя, k — переменная интегрирования.

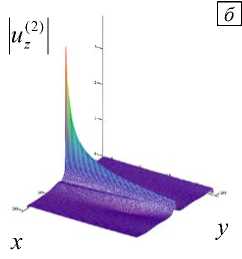
Результаты вычислений по формулам (10), соответствующие скачку скорости SH - волн cJC_t = 0,9, относительной удаленности источника от границы to HJC, = 11,1 л и мощности слоя to H/c, = 5 п представлены на рисунке 4, а . Из анализа картин распределения волновых амплитуд следует, что для 1 -й области при удалении от источника, кроме спада поля u_z ⁽¹⁾ по уровню, характерно присутствие периодической последовательности максимумов в угловых секторах, расположенных веером, а в дальнем поле переходящих в лепестки диаграммы направленности, что качественно отвечает ранее полученным результатам. Важно, что масштаб, используемый по продольной координате x , одинаков для всех рисунков, в то время как масштаб по поперечной координате y на рисунке 4, б в сто раз более крупный, чем на рисунке 4, а . С учетом указанной разницы в масштабах, легко заключить, что в двумерном случае по мере удаления от источника и приближения к границе слоя во 2 -й области амплитуда поля u_z ⁽²⁾ снижается по координате y более резко, чем на рисунке 4, а . Демонстрируемая картина соответствует конфигурации поля вблизи источника при его расположении около границы инородного слоя. Таким образом, как для поперечных волн, так и для акустических визуализация пространственного распределения амплитуды рассеянного волнового поля u_z , рассчитанного по первым двум формулам (10), позволяет видеть некоторые характерные особенности, способные служить информативными признаками, указывающими на принципиальную возможность неразрушающего дистанционного прогноза присутствия неоднородности. К числу информативных признаков относятся количество лепестков, их амплитуда и темп спада рассеянного поля. Получение подобной картины, например, в экспериментах по геофизической разведке или при поиске нефтезалежи, возможно путем регистрации пространственного амплитудного распределения сейсмоакустического поля антенной решеткой геофонов, устанавливаемых в скважине, приближающейся к продуктивному слою или пересекающей его. При этом предполагается, что и источник колебаний размещен на незначительном удалении от границы зондируемого слоя либо в той же, либо в соседней скважине [5].

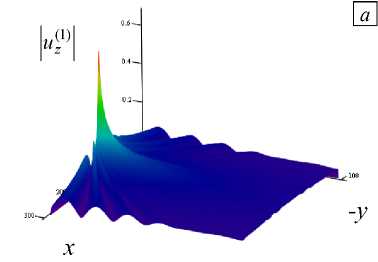
Рис. 4. Фрагменты пространственного распределения волновых амплитуд u_z в относительных единицах: в 1 -й ( а ), и 2 -й ( б ) областях

В настоящее время данный класс задач (класс прямых задач), как правило, решается с привлечением конечно-элементных методов, которые кладутся в основу соответствующих алгоритмов, реализуемых в пакетах вычислительных программ для современных компьютеров. В данной работе показано, что использование аналитического подхода с последующим применением вычислительных программ, но ориентированных на расчет интегральных выражений, а далее — современных графических средств визуализации результатов, то есть к построению изображения пространственного амплитудного распределения, также может обеспечить значительное продвижение в их решении. Сопоставление решений, получаемых обоими путями (алгоритмическими и аналитическими подходами), должно привести к наиболее достоверным результатам анализа проблемы, которые позволят совместить как наглядность и детальность решения математически сформулированных прямых задач, так и возможность выявления физической сущности процессов, лежащих в основе сейсмоакустического зондирования.