Моделирование шумообразования тонких пил

Введение. Тонкие пилы применяются в ленточнопильных металлорежущих и деревообрабатывающих станках, а также лесопильных рамах. Несмотря на различное функциональное назначение, расчет виброакустических характеристик может быть выполнен с единых позиций.

Конструктивные особенности ленточнопильных станков заключаются в отсутствии высокоскоростных зубчатых передач в приводах, наличии длинной и маложесткой ленточной пилы, а также в широком классе конфигураций и размеров отрезаемых заготовок. Эти особенности позволяют предположить, что в формировании звукового поля станка в целом доминирует звуковое излучение самой пилы, – в первую очередь, и в ряде случаев отрезаемой заготовки.

Поскольку и у пилы, и у отрезаемых заготовок длина существенно больше размеров поперечного сечения, то в качестве модели источника шума принят линейный источник, звуковое давление которого на основе работ [1, 2] определяется следующей зависимостью:

P = 9,5 V ( f_kFl ) ^0,5

где V k – виброскорость (м/c) на каждой собственной частоте колебаний f k (Гц); F – площадь поверхности источника шума, м²; l – длина источника, м.

Вывод зависимостей виброскоростей тонких пил. В ленточных пилах для устойчивой их работы создается предварительное натяжение. Собственные частоты колебаний пилы как полосы с предварительным натяжением определяются по формуле fk

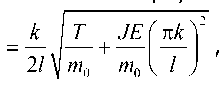
k T JE (n k ?

2 l\m ₀   m ₀ ^ l

где T – натяжение пилы, Н; m 0 – распределенная масса, кг/м; J – момент инерции, м⁴; Е – модуль упругости, Па; k – коэффициент, характеризующий соответствующую собственную частоту колебаний; l – длина источника, м.

Подставив в формулу собственных частот колебаний значения модуля упругости, плотности, момента инерции, получим для пилы следующую зависимость:

2,2 - 10 7 l^ k I + 1,3 - 10 - 4 — , , I l J , bh

где b и h – толщина и высота пилы соответственно, м.

Следовательно, для теоретического определения спектров шума, создаваемых звуковым излучением пилы, необходимо определить скорости колебаний на собственных частотах.

8 ( x — x о ) ,

Дифференциальное уравнение изгибных колебаний имеет вид д ² y + EJ d ⁴ y _ T d ² y _ p d t ² m 0 d x ⁴ m 0 d x ² m 0

где Р - сила резания, Н; S ( x — x 0 ) - дельта функция, смещенная по координате.

Для расчета виброакустических характеристик пилы использован подход, развитый в работе [2] и основанный на представлении силы резания с использованием дельта-функции. В отличие от токарной, фрезерной, шлифовальной обработки (где сила резания перемещается вдоль заготовки) на ленточнопильных станках (несмотря на поступательное перемещение пилы) координаты приложения пилы усилий на каждом зубе остаются постоянными относительно мест закрепления пилы. Кроме этого, число зубьев в зоне резания изменяется. Поэтому фактически силу представим как сумму дельта функций. Изгибная жесткость пилы намного меньше жесткости опор. Поэтому краевые условия закрепления соответствуют жесткому защемлению. Решив дифференциальное уравнение (4) методом разделения переменных, получим выражение виброскоростей:

^д У - ( x, t ) д t

—

S

3 -^    * to

t ^*

О ЛАЛ 1 ¹

. 3 ^{n k}l,       . 3 ^{n k} / , i \

Sin ~p + Sin — ( 1₁ + t ) + ...

² m о ¹ k _ i EJ Г п k

m ₀ I 1

4          / x 7

I + T (t 1

m ₀ 1 1 J

-

s A ²

* t ^*

sin

S, hh t * t (q -) t * ,

д У 2 ( x , t ) д t

P ^S _*

-

t

to

2 m ₀ l

I

k = 1

. 3 Л kl,       . 3 Л k / ,      i \

Sin —p + Sin — ( 1 ₁ + t ) + ...

EJ Г 3 п k Y T Г 3 п k Y Г S

1 I ⁺I I ^— I m ₀ V 1 J m ₀ V 1 J 1 1

sin

S, hh

t* t ⁽ q ^{- )} t* ’

где S – подача пилы, м/c; t ^* – шаг зубьев, м; h – ширина пропила (высота для вертикальнопильных станков), м; q – номер зуба в зоне резания.

Эти выражения в явной форме не учитывают диссипативную функцию, фактически определяемую эффективным коэффициентом потерь колебательной энергии. Для учета потерь колебательной энергии зададим модуль упругости в комплексной форме E ? _ E ( 1 + i n ) .

С учетом этой зависимости выражения действительной части виброскорости примут вид:

дУ1 (x, t) _

—

д t

1,5 ^ S * I^ m 0 1t t _ 7

■ 3 ^{П k1} l .

Sin —^- + Sin l

EJ Гпk Y T Гпk A2

--------1 I ⁺-------1 I

m 0 V 1 J m 0 V 1 J

—

m ₀

S A t * J

Г EJ

— x

+ n

V ^m 0 J

n k Y

J

S         2n x Sin -*t— (q — -)— coSФ,

S

2 n

t

t

;

дУ2 ( x, t ) д t

—

0,5 - PI * I to: m 0 1t t _ T

■ 3 ^{П k1} l

Sin —^- + Sin l

EJ Г 3 n k Y

m ₀

— I + —
1 J	m 0
	■ S,
x Sin	, t *

—

t Г 3 n k Y

1 ¹

—

^S A t * J

Г EJ

x

+ n—

V m 0 J

3 k k Y

J

/   n 2п

⁽ q ^{— -)} — cos ф;

;

EJ Гл k Л2

nI I

Ф = arctg

m 0 V l )

EJГпk? T ГлkY ГSVI I +I I -I 7* Im 0 V l ) m 0 V l 2 V t 2

Для расчетов уровней шума практический интерес представляет максимальное значение уровней звукового давления и, соответственно, виброскорости. Поэтому следует определить мак-д Уз    дУэ симальное значение величин — и — за время резания, т. е. при 0 < t < t , где tpe3 - время д t     д t                                                  рез резания.

Виброскорость пилы на каждой собственной частоте колебаний определяется по формуле д у       ду₂

V, = ^-1 max + ^-^max .

^k д t          д t

Для уровней звукового давления, создаваемых пилой, получено следующее выражение:

Р

L_k = 20 lg------- k         20 - 10 ^{- 5}

= 20lg V_k - 20lg r + 10lg khl + 5lg 2,2 - 10 7 l^ k I + 1,3 - 10

—

4 T bh

.

Дальнейшая процедура расчета сводится к следующему алгоритму:

• -    определяется спектр собственных частот колебаний пилы;

• -    определяется количество собственных частот колебаний, попадающих в соответствующие октавные полосы частот;

• -    на каждой собственной частоте колебаний определяются уровни звукового давления;

• -    по количеству собственных частот колебаний, попавших в соответствующую октавную полосу, определяются энергетическим суммированием усредненные по октаве уровни звукового давления по формуле

k

Lokt = 10lg ^100,1 Lk , где k – количество собственных частот колебаний пилы, попавших в соответствующую октавную полосу.

Учет эффективного коэффициента потерь колебательной энергии позволяет решить задачу снижения шума в самом источнике его возникновения путем выбора рациональных параметров системы виброзащиты. Для этого в левую часть выражения (7) подставим предельно допустимые октавные уровни звукового давления и получим зависимость виброскоростей пилы, обеспечивающих выполнение санитарных норм шума:

lg V_k = 0,05 L C + 20 lg r - 0,5 lg khl - 0,25 lg

2,2 - 10 7 l^ k I + 1,3 - 10 ^-4 — , V l I , bh

На основе этой зависимости возможно осуществить выбор параметров системы виброзащиты, обеспечивающей выполнение санитарных норм шума.

Заключение. Полученные зависимости позволяют при проектировании ленточнопильных станков определить расчетным путем ожидаемые уровни шума, сравнить их с предельно допустимыми значениями и выявить частотные диапазоны, в которых наблюдаются превышения над санитарными нормами.