Моделирование сигнала ВНЗ радара SuperDARN в присутствии движущейся среднемасштабной неоднородности во время падения метеорита «Челябинск»

Радар российского сегмента сети когерентных радаров SuperDARN расположен приблизительно в 200 км к северу от предполагаемого места взрыва и падения метеорита «Челябинск» [Berngardt et al., 2013a]. Радар представляет собой аналог радаров CUTLASS [Lester et al., 2004] и размещен ИСЗФ СО РАН на территории обсерватории «Арти» Института геофизики УрО РАН. Оборудование радара закуплено в Университете Лейстера (Великобритания) на средства СО РАН, а развертывание радара было проведено при финансовой поддержке Российской гидрометеослужбы. Радар был запущен на постоянный режим работы 17.12.2012 г.

Основа работы радара – наблюдение характеристик обратно рассеянного сигнала одновременно в режимах возвратно-наклонного зондирования (ВНЗ) и обратного рассеяния на мелкомасштабных неоднородностях ионосферы [Chisham et al., 2007], что позволяет проводить одновременную оценку характеристик как фоновой ионосферы методом ВНЗ, так и мелкомасштабных неоднородностей методом обратного рассеяния.

Антенная система радара представляет собой фазированную антенную решетку с сектором сканирования порядка 50° и шириной лепестка порядка 3°. Сканирование всего сектора ведется примерно в течение 60 с с анализом каждого из 16 фиксированных направлений примерно в течение 3–4 с. Характери- стики антенной системы таковы, что обратный лепесток диаграммы направленности (ДН) составляет порядка –(3÷10) дБ по мощности от основного лепестка в зависимости от частоты. В вертикальной плоскости радар имеет широкую ДН, рабочим можно считать диапазон углов излучения от 5º до 45º.

Зона падения метеорита расположена на 200 км к югу от радара, в зоне заднего лепестка ДН. На рис. 1 приведена геометрия эксперимента. Вследствие необычайной близости радара к месту падения метеорита, высокого пространственного и временного

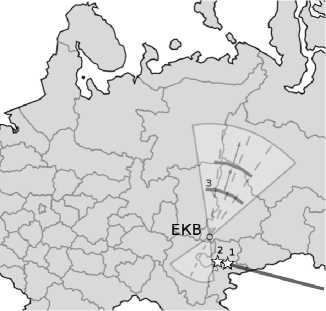
Рис . 1 . Геометрия эксперимента. Черная линия – траектория метеорита, 1 – место взрыва метеорита, 2 – место предполагаемого падения, 3 – восстановленный фронт неоднородности. Секторами обозначены зоны сканирования радара главным и задним лепестками ДН.

разрешения радар является, по-видимому, единственной установкой для исследования ионосферных эффектов на минимальных расстояниях от места взрыва и падения метеорита.

При наблюдении ионосферных эффектов, связанных с падением метеорита «Челябинск», рабочая частота радара была 10 МГц. Зондирующий сигнал радара SuperDARN является последовательностью импульсов специального вида [Chisham et al., 2007]. Длительность элементарного импульса радара на момент падения метеорита составляла 400 мкс [Berngardt et al., 2013a, b]. Это соответствует разрешению по групповому пути 60 км в диапазоне дальностей 400–3500 км.

На рис. 2, a показана мощность ВНЗ-сигнала за 15.02.2013 г. (03:30–06:00 UT), а на рис. 2, б – усредненная мощность за пять ближайших магнитоспокойных дней: 9–12, 18.02.2013 г. Данные были дополнительно усреднены по всем азимутам, что позволило выделить эффекты, связанные с радиальным распространением волны. Видно наличие явного эффекта в день падения метеорита 15.02.2013 г. по сравнению с остальными днями. Эффект заключается в появлении нескольких дополнительных удаляющихся зон обратного рассеяния приблизительно в течение 60 мин после падения метеорита.

На рис. 2, в приведены данные за период 03:30– 06:00 UT по отклонению мощности ВНЗ-сигнала 15.02.2013 г. от усредненной мощности за пять ближайших магнитоспокойных дней. На рис. 2, г показано сечение распределения скоростей отдельно для данных на первом и втором скачке.

При диагностике ионосферы радарами SuperDARN эффект возникновения нерегулярных наклонных треков на диаграмме дальность–время–интенсив-ность (ДВИ) возникает часто и связывается с появлениями перемещающихся ионосферных возмущений (ПИВ). Он может быть связан с наблюдениями ПИВ, вызванных как естественными ионосферными процессами [Stocker et al., 2000], так и землетрясениями [Ogawa et al., 2012]. Попытки объяснения подобных треков приведены, например, в работе [Stocker et al., 2000] с использованием моделирования методом геометрической оптики (ГО).

Особенность эффекта, наблюдаемого 15.02.2013 г., заключается в том, что стандартный трек, формирующийся за счет фокусировки на границе мертвой зоны (рис. 2, б ), раздваивается (рис. 2, a ), что говорит о возможном возникновении ионосферной неоднородности, формирующей дополнительный путь распространения сигнала. Движение такой неоднородности приводит к увеличению дальности до нового трека, в то время как трек, соответствующий фоновой ионосфере, находится практически на месте. Формирование подобных неоднородностей нередко во время мощных взрывов и землетрясений [Afraimovich et al., 2001; Akhmedov, Kunitsyn, 2004].

Попытки объяснения подобных треков на данных радаров SuperDARN приведены, например, в работе [Stocker et al., 2000] с использованием моделирования методом ГО. В работе показано, что при возрастании амплитуды возмущения возникают дополнительные зоны фокусировки сигнала, вызывающие увеличение принимаемой мощности сигнала ВНЗ и формирование дополнительных треков на диаграмме ДВИ. Интерес вызывает то, что при ам- плитуде возмущения более 15–20 % на временной диаграмме зависимости мощности принимаемого радаром сигнала ВНЗ от группового пути возникают два дополнительных наклонных трека с разными кажущимися скоростями [Stocker et al., 2000].

В нашем случае возмущение электронной концентрации может быть велико [Тертышников и др., 2013; Berngardt et al., 2013a], и поэтому стоит исследовать вопрос влияния распространения уединенной неоднородности на сигнал SuperDARN более детально. Это необходимо для выяснения того, какие наблюдаемые моды связаны с реальным движением неоднородности, а какие являются лишь эффектом, связанным с особенностями метода и постановкой эксперимента.

Метод моделирования

В рамках задачи проводилось моделирование зависимости мощности сигнала ВНЗ от времени и дальности в присутствии неоднородности, распространяющейся от места расположения радара радиально. Моделирование проводилось в рамках метода ГО посредством решения системы лучевых уравнений [Кравцов, 1980; Чернов, 1975].

Для сравнения с экспериментальными данными необходимо оценить мощность сигнала ВНЗ как функцию времени и дальности. При моделировании рассчитывались зоны фокусировки сигнала, в которых мощность сигнала ВНЗ возрастает. Положение зон фокусировки определялось методом ГО. Качественная зависимость мощности от дальности получалась суммированием лучей, попадающих в 60-километровые интервалы по групповому пути, с учетом их веса. Вес луча зависел от угла излучения и задавался ДН приемно-передающей антенны. Эта методика аналогична использованной в работе [Stocker et al., 2000] и позволяет качественно рассматривать поведение зон фокусировок и увеличения мощности сигнала, хотя и не позволяет получать количественную оценку мощности сигнала.

Моделирование распространения сигнала проводилось в приближении ГО для холодной изотропной плазмы. Для этого был модифицирован метод, ранее использовавшийся для расчета зон эффективной работы данных радаров [Кутелев, Куркин, 2010]. Вследствие центральной симметрии рассматривалась двумерная постановка задачи в изотропной ионосфере, предполагающая также отсутствие азимутальной рефракции. В этом случае уравнение траектории имеет вид

∂ R

= p_R , ∂τ

∂ n   1

=   p_n ,

∂τ   R

∂ p_{R = -} f e ∂ f e ₊ 1

∂τ f ² ∂ R  R p

dPn = 1 ( fe dfe дт R ^ f2 dn pr pn

где R и φ – полярные координаты, τ – групповой путь луча, f e – плазменная частота в данной точке, f – частота передатчика, p R и p φ – компоненты направляющего импульса.

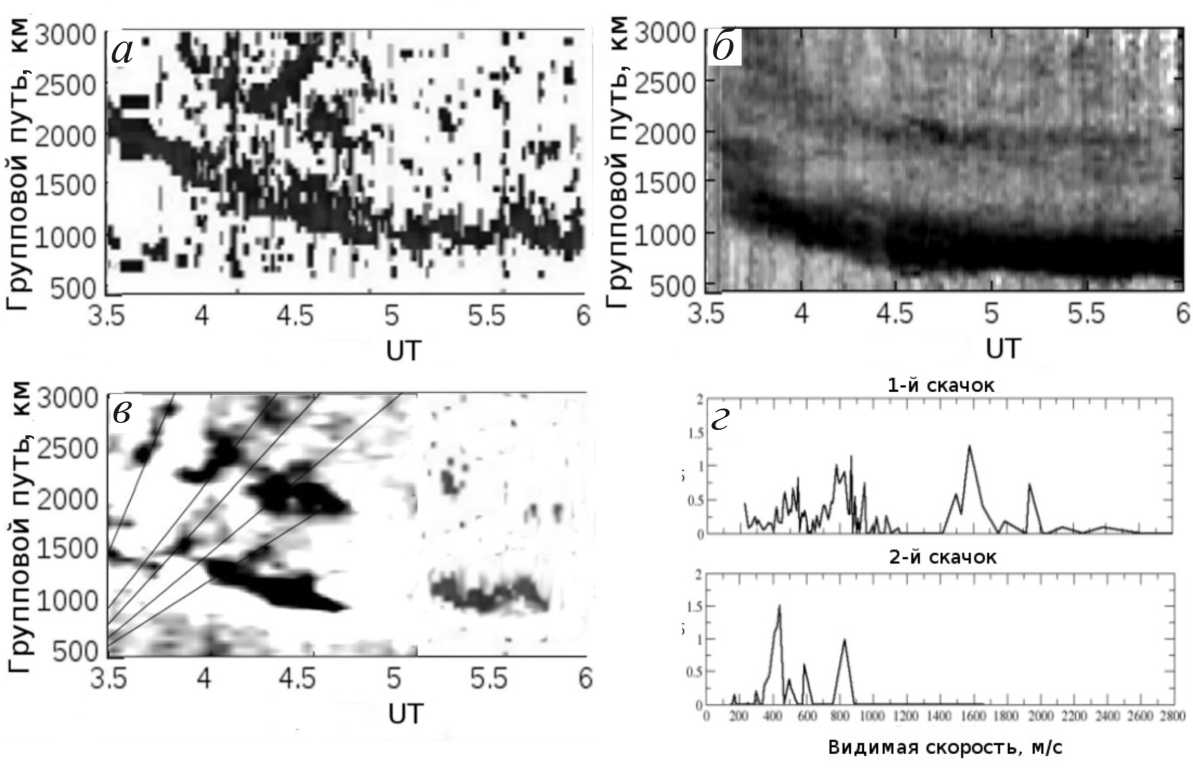
Рис . 2. Сравнение ВНЗ-сигнала радара SuperDARN 15.02.2013 г. и референтного значения за 9–12, 18.02.2013 г., усредненное по азимутам: a – мощность ВНЗ-сигнала 15.02.2013 г.; б – усредненная мощность ВНЗ-сигнала за пять магнитоспокойных дней; в – отклонение мощности ВНЗ-сигнала 15.02.2013 г. от усредненной мощности за пять ближайших магнитоспокойных дней; г – сечение распределения видимых скоростей в ВНЗ-сигнале.

Для получения зависимости группового пути ВНЗ-сигнала от угла излучения в приближении первого скачка строилась траектория каждого луча до момента возврата на Землю.

В качестве модельной среды рассматривалась ионосфера, являющаяся суперпозицией фоновой электронной концентрации и динамичного среднемасштабного возмущения электронной концентрации, связанного с взрывом метеороида, определяемым относительным изменением электронной концентрации, распространяющимся радиально от места взрыва. Плавная неоднородность и динамика фоновой электронной концентрации определяются суточным и широтно-долготным ходом ионосферных параметров. Среднемасштабное возмущение электронной концентрации представляет собой цилиндрическую волну, распространяющуюся во всей толще ионосферы радиально от места взрыва. Подобная модель часто используется при интерпретации эффектов, связанных с запусками ракет [Afraimovich, 2001] и землетрясениями [Afraimovich et al., 2002; Nishitani et al., 2012]. Амплитуда возмущения пропорциональна фоновой электронной концентрации на соответствующей высоте.

Таким образом, модель пространственно-временного хода электронной концентрации имеет вид

N0(d, h, t)=N0(d, h, t)(1+ΔN(d, t)), (2) где N0(d, h, t) – фоновая электронная концентрация, ΔN(d, t) – относительное среднемасштабное изменение фоновой электронной концентрации; h – высота точки наблюдения эффекта, d – расстояние по земле от места взрыва до точки наблюдения эффекта.

Плазменная частота f e связана с электронной концентрацией известным соотношением [Дэвис, 1973]

f_e ²( d,h,t ) = 80.6 N ( d,h,t ).                        (3)

В качестве модели фоновой ионосферы использовалась модель IRI-2007 [Bilitza, 2008] на дату 15.02.2013 г., скорректированная по результатам измерений в обсерватории «Арти». Данные ионозонда о критической частоте F2-слоя над обсерваторией сравнивались с критической частотой по модели IRI. Коэффициент коррекции на текущий момент времени вычислялся как отношение экспериментальной критической частоты к модельной. Для определения профиля электронной концентрации во всем исследуемом пространстве f _oF2 определялась по данным модели IRI и корректировалась пропорционально соотношению модельной и экспериментально измеренной f _oF2 по данным ионозонда. Полученные значения f _oF2 использовались для получения модельных профилей электронной концентрации в каждой точке пространства с использованием внутреннего алгоритма коррекции IRI-2007 по f _oF2.

В качестве моделей возмущения электронной концентрации рассматривались два варианта уединенных неоднородностей – гауссов импульс и импульс N-типа. Использование гауссова импульса позволяет оценить влияние каждого из параметров волны (скорости, амплитуды и характерного масштаба) на результат эксперимента. Импульс N-типа наиболее типичен для ударных волн в ионосфере, наблюдаемых, например, после землетрясений [Afraimovich et al., 2002; Astafyeva, Heki, 2009], и поэтому более приближен к реальности.

Гауссов импульс, распространяющийся радиально от места взрыва, имел вид

Δ N ( d, t ) = δexp

( d — V TiD t ) 2 2 H ²

Импульс N-типа имел вид:

Δ N ( d, t ) = δ ^{( TID )} exp

( d ^- V_T D t ) 2 2 H ²

В обеих моделях Δ N – относительное возмущение электронной концентрации, δ – амплитуда возмущения, d – расстояние на земле от места взрыва до точки наблюдения эффекта, V _TID – групповая скорость возмущения, H – пространственный размер.

Односкачковое распространение

Результаты моделирования для гауссовой волны

Для исследования применимости данной модели к интерпретации экспериментальных данных было проведено моделирование в модели гауссовой неоднородности (4) с учетом только односкачкового распространения. В рабочем интервале углов места излучения 5–45° рассчитывался набор лучей с шагом по углу излучения 0.01 ° . Качественная зависимость мощности от дальности получалась суммированием лучей, попадающих в 60-километровые интервалы по групповому пути. Для первоначального моделирования были выбраны следующие параметры неоднородности: δ=0.44; V TID =400 м/с; H =100 км.

Предварительное моделирование распространения сигнала в фоновой ионосфере (при Δ N =0) и в ионосфере в присутствии радиально распространяющейся неоднородности приведено на рис. 3. Сравнение распространения в фоновой ионосфере (см. рис. 3, a ) показывает качественное совпадение динамики перемещения максимума мощности сигнала (основного трека сигнала, связанного с фокусировкой на границе мертвой зоны [Иванов и др., 2009]). Сравнение распространения в возмущенной ионосфере (см. рис. 3, б ) показывает качественное совпадение динамики перемещения основного максимума мощности сигнала, связанного с фоновыми условиями, и дополнительных максимумов, связанных с существованием среднемасштабного возмущения. Это позволяет сформулировать задачу определения параметров неоднородности, наиболее хорошо описывающей экспериментальные наблюдения.

Для анализа влияния параметров возмущения на экспериментальные данные было проведено детальное моделирование при различных параметрах возмущения. Результаты моделирования в присутствии неоднородности гауссова типа приведены на рис. 4, a–г. Влияние неоднородности проявилось в качественном изменении суточного хода главного максимума и минимального группового пути. На рис. 4, a–г различимы несколько наклонных треков – перемещающихся зон дополнительной фокусировки, связанных с распространением неоднородности. Количество треков и их характеристики определяются параметрами неоднородности – ее размером, скоростью и амплитудой.

На рис. 4, a показан результат моделирования прохождения неоднородности с параметрами V _TID=400 м/с, H =100 км и δ=44 %. Различимы четыре трека. Первый по времени трек выражен слабее остальных, и наблюдаемая скорость перемещения зон фокусировки, рассчитываемая, как наклон треков, также различна: первый трек самый быстрый, второй и третий треки имеют примерно одинаковую скорость, четвертый трек самый медленный.

На рис. 4, б показан результат моделирования влияния более компактной по сравнению с показанной на рис. 3, a неоднородности с характерным масштабом H =50 км. Количество треков увеличилось до шести, сгруппированных попарно. Качественно соотношение видимых скоростей треков не изменилось. Как показал анализ, дальнейшее уменьшение масштаба не приводит к увеличению числа треков, хотя они становятся при этом более ярко выраженными.

На рис. 4, в показан результат моделирования более протяженного по сравнению с показанной на рис. 4, a возмущения. Видно, что изменения мощности незначительные и слишком плавные для идентификации их в качестве треков. Однако возмущение суточного хода главного максимума присутствует. Из этого можно заключить, что для возникновения треков необходимо наличие сильного градиента электронной плотности вдоль трассы.

На рис. 4, г представлены результаты моделирования для более медленной (по сравнению с рис. 4, a ) неоднородности, перемещающейся со скоростью 200 м/с. Видно, что наклон треков изменился, что вызвано изменением скорости перемещения зон фокусировки сигнала. Однако эти скорости не совпадают со скоростью ПИВ. Кажущаяся скорость 1-го трека значительно превосходит скорость ПИВ, скорости 2-го и 3-го треков примерно в 2 раза больше. Скорость 4-го трека превышает скорость неоднородности примерно в 1.5 раза.

По результатам моделирования можно сделать следующие выводы.

• 1.    Наличие возмущения гауссова типа приводит к двум типам изменений в пространственновременной диаграмме мощности обратно рассеянного сигнала: изменению пространственно-временного хода главного максимума рассеянного сигнала и появлению нескольких зон дополнительной фокусировки (треков).

• 2.    Количество и выраженность треков определяется градиентом электронной плотности вдоль трассы: чем больше амплитуда и меньше размер неоднородности, тем отчетливее проявляются треки.

• 3.    Наблюдаемая скорость треков зависит от скорости ПИВ, хотя и не равна ей.

Трассировка

Для объяснения полученных выше результатов была проведена трассировка лучей, создающих зоны дополнительной фокусировки. Для этого в профиле мощности определялся локальный максимум, связанный с конкретным треком, и выделялся диапазон углов излучения, соответствующий данному групповому пути. Изображение соответствующих лучей наклады-

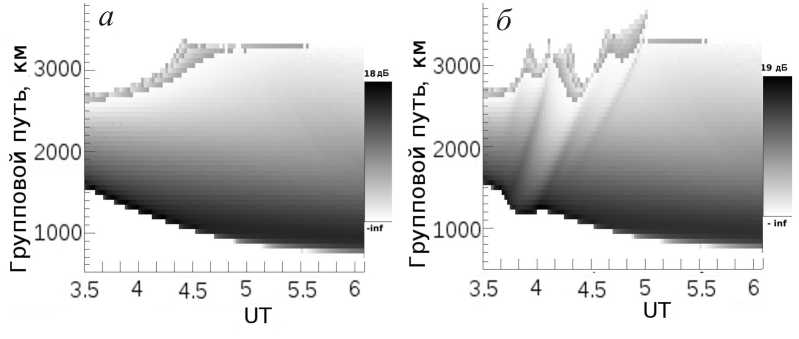
Рис . 3. Смоделированные диаграммы мощности ВНЗ-сигнала для различных условий в ионосфере: a – фоновая ионосфера по модели IRI-2007 на 15.02.2013 г.; б – появление треков на модельной диаграмме при наличии гауссова возмущения (δ=0.44, V _TID =400 м/с, H =100 км).

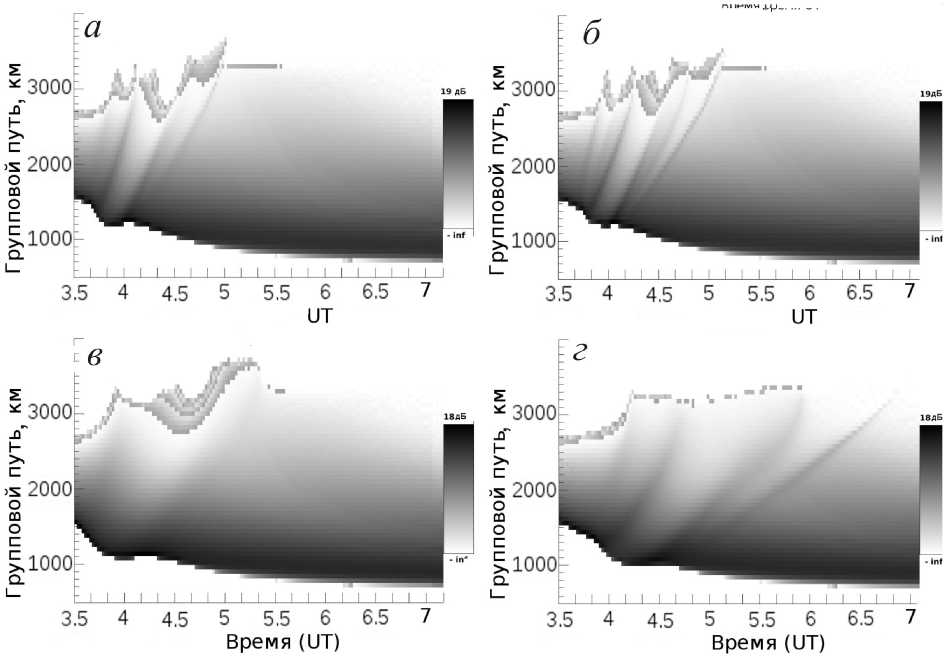
Рис . 4. Диаграммы мощности ВНЗ-сигнала для различных условий в ионосфере: наличие гауссова возмущения, δ=0.44, V TID =400 м/с, H =100 км ( a ); δ=0.44, V TID =400 м/с, H =50 км (б); δ=0.44, V TID =400 м/с, H =300 км (в); δ=0.44, V TID =200 м/с, H =100 км (г).

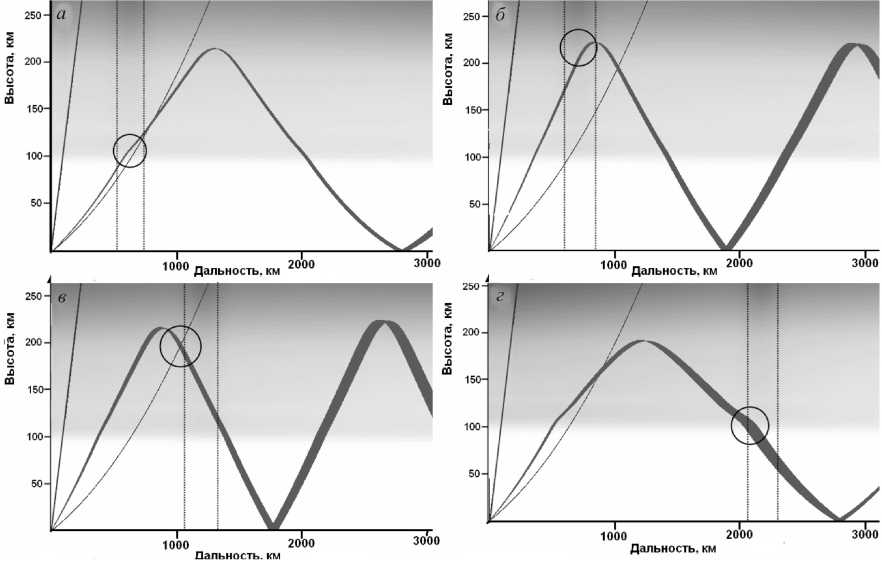
Рис . 5. Лучи, формирующие различные треки при прохождении гауссовой неоднородности (δ=0.44, V _TID =400 м/с, H =100 км): фокусировка в E-слое на восходящей части траектории (а); в F-слое на восходящей части траектории (б); в F-слое на нисходящей части траектории (в); в E-слое на нисходящей части траектории (г).

валось на сечение электронной концентрации. Некоторые результаты для различных моментов времени и разных треков трассировки приведены на рис. 5.

Из результатов моделирования видно, что первый по времени трек формируется за счет фокусировки в Е-слое на восходящей части траектории. Второй и третий трек формируются за счет фокусировки в F-слое на участках с наибольшим градиентом электронной плотности в задней и передней частях неоднородности соответственно. Самый поздний трек формируется за счет фокусировки в Е-слое на нисходящем участке траектории.

Знание механизма формирования треков позволяет нам качественно объяснить результаты моделирования, полученные выше. Фокусировка происходит в областях наибольшего градиента электронной плотности, следовательно, амплитуда неоднородности и ее геометрический размер являются ключевыми параметрами для генерации треков. Фокусировка может происходить и на переднем, и на заднем градиенте электронной плотности, поэтому всего может быть шесть треков – два от F-слоя и четыре от E-слоя, так как E-слой луч пересекает два раза. Ослабление крайних треков при возрастании рабочей частоты радара объясняется более низкой диэлектрической проницаемостью в E-слое.

Для получения качественных формул, позволяющих оценить скорость перемещения ПИВ по скорости движения зон фокусировки, используем геометрический подход на основе теоремы Брейта– Тьюва для плоскослоистой среды [Дэвис, 1973] и сравним расчеты, полученные на его основе, с результатами численного моделирования.

Плоскослоистый случай проиллюстрирован на рис. 6. Данная теорема устанавливает равенство между групповым путем криволинейного луча в изотропной ионосфере и суммарной длиной двух соответствующих сторон треугольника, описанного вокруг луча.

В плоскослоистой среде групповой путь луча до возвращения на землю равен

P= у/ ( 2 H f ) 2 + D2 , (6)

где P – групповой путь, D – дальность по земле, H F – эффективная (кажущаяся) высота отражения в F-слое. Дифференцируя данное выражение по времени, получим выражение, связывающее скорость неоднородности со скоростью наблюдаемого трека:

V трека

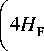
d H f +D d D ^ d t        d t J

7 (2 H f ) ² +D²

Здесь V трека =∂ Р /∂ t – это кажущаяся скорость трека про данным радара SuperDARN, ∂ D /∂ t – скорость перемещения зоны фокусировки вдоль земли, ∂ H F /∂ t – скорость изменения высоты точки отражения.

Из анализа (7) видно, что на больших дальностях D и при больших скоростях перемещения ∂ D /∂ t неоднородности второй член в (7) значительно превышает первый и эффектами, связанными с суточными изменениями фоновой ионосферы, при расчете скорости ПИВ можно пренебречь.

Рассмотрим фокусировку в F-слое. В этом случае из подобия треугольников на рис. 6, в видно, что скорость перемещения зоны фокусировки и скорость ПИВ V _TID связаны соотношением:

V TID =0.5(∂ D /∂ t ). (8)

Подставляя (8) в (7) и пренебрегая dH _F/ dt , получаем качественное соотношение между скоростью трека V _трека и скоростью ПИВ V _TID

V трека

D

⁼ TID _P ⁼ TID

D у/ (2 Hf )2 +D2

Это выражение при увеличении дальности D асимптотически стремится к удвоенной скорости ПИВ. Поскольку типичная высота отражения составляет 200 км, а дальность появления зон фокусировки превышает 1000 км, данное выражение отличается от удвоенной скорости не более чем на 10 % и может быть использовано для качественных оценок.

Аналогично можно провести оценки влияния различных фокусировок на кажущуюся скорость трека, используя подобие треугольников на рис. 6, а , б . Для этого достаточно связать перемещения точки фокусировки в E-слое и точки отражения в F-слое. Для фокусировки на восходящей части траектории (рис. 6, а ) коэффициент пропорциональности равен H _F/ H _E, где H _E – высота фокусировки в E-слое. Для фокусировки на нисходящей части траектории (рис. 6, б ) коэффициент пропорциональности составляет H F /(2 H F – H E ).

Таким образом, мы получаем соотношения между скоростями ПИВ V TID и эффективными скоростями треков V i :

V 1

= ^ TID

2 H _F

H E

2 H

F

^V 2,3 ^{= V} TID       ^{=  V} TID ^,

H _F

V 4

= V _TID

2 H _F

2 H _F - H_E

FE

Из полученных качественных оценок видно, что проще всего оценивать скорость неоднородности по скоростям второго и третьего трека V 2 , V 3 , так как их скорость примерно в два раза выше реальной скорости ПИВ V TID . Данный подход не учитывает дополнительных отличий эксперимента от плоскослоистого случая, таких как неравномерное движение неоднородности вдоль трассы, кривизна земной поверхности, градиенты в ионосфере, движения ионосферных слоев и так далее, однако пригоден для качественных оценок.

Для проверки валидности полученных для плоскослоистой среды качественных соотношений (10) в случае сферически-слоистой среды было проведено сравнение с результатами численного моделирования. Оно показало, что учет сферической геометрии задачи и горизонтальной неоднородности ионосферы приводит к отклонению формы трека от прямой, особенно при больших групповых путях, когда отклонение от плоскослоистого случая сущест-

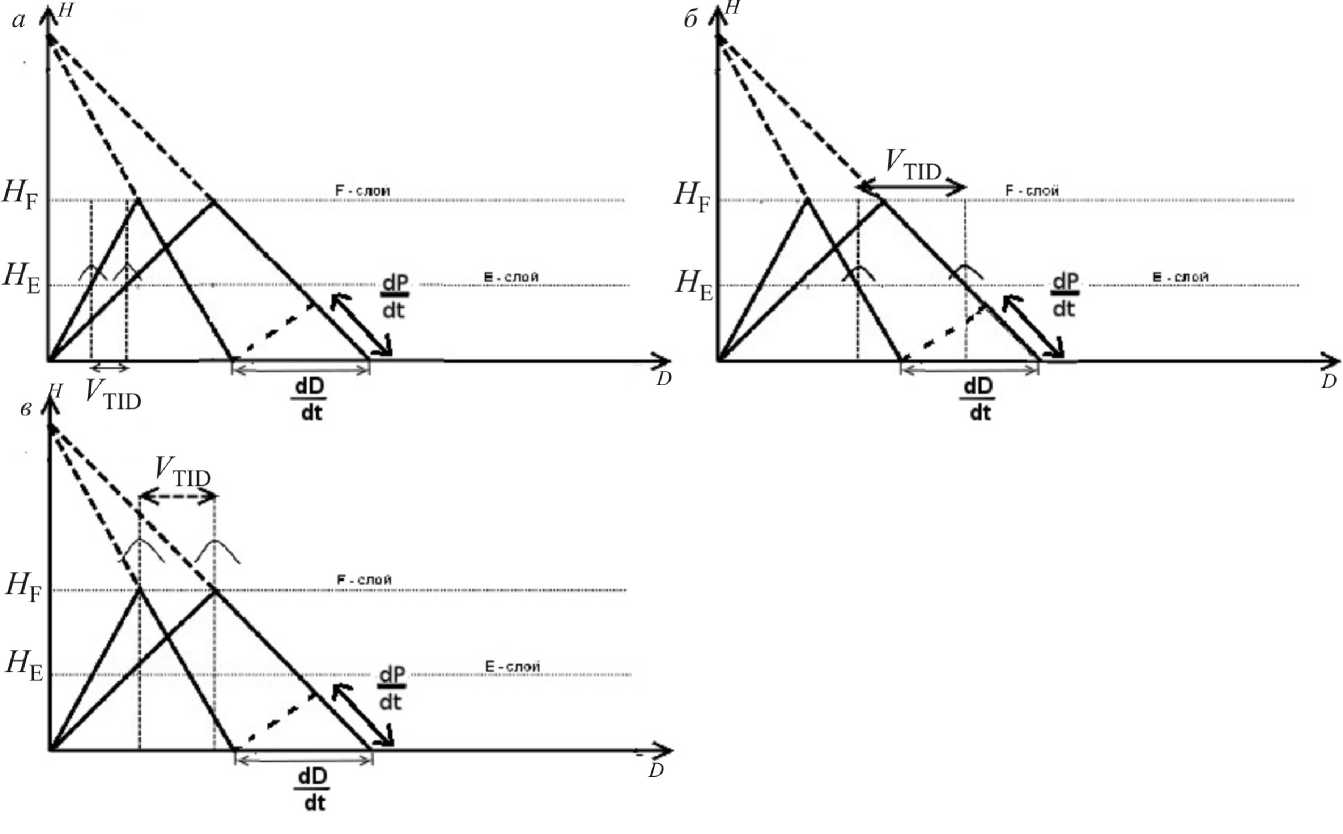
Рис . 6. Связь перемещения ПИВ и смещения зоны фокусировки сигнала для случая плоской отражающей поверхности при различных положениях неоднородности: фокусировка в E-слое на восходящей части траектории (трек 1) ( a ); в F-слое (треки 2, 3) (б); в E-слое на нисходящей части траектории (трек 4) (в).

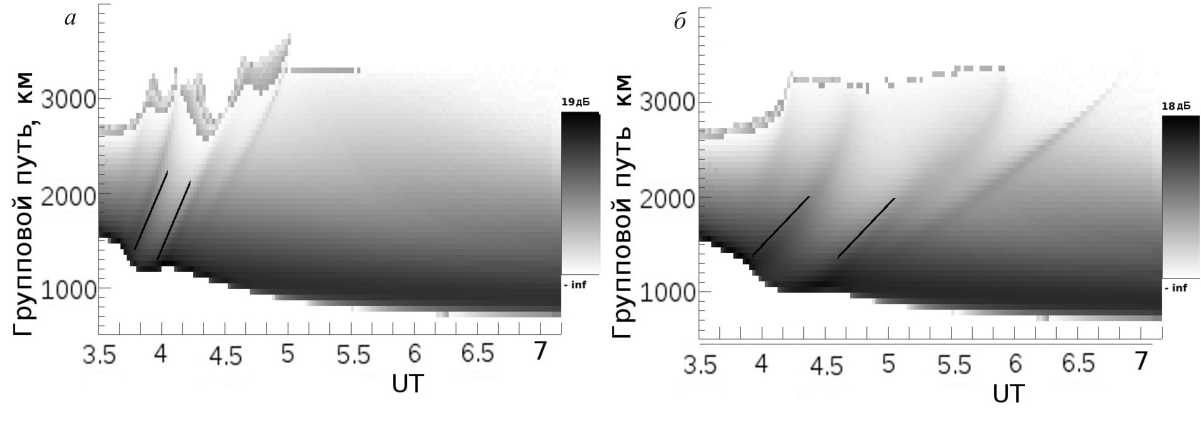
Рис . 7. Диаграммы мощности ВНЗ-сигнала для ПИВ с различными скоростями: a – 400 м/с, б – 200 м/с.

венно. Это приводит к ошибкам применения качественных формул (10) на больших групповых путях. На рис. 7 показаны диаграммы мощности с нанесенными отрезками, соответствующими удвоенной скорости ПИВ. Видно, что сформулированный качественный метод оценки скорости ПИВ действительно верен, но лишь на относительно малых групповых путях до точки рассеяния сигнала от земли (<2000 км), когда отличием геометрии от плоскослоистой можно пренебречь.

Результаты моделирования для N- образного возмущения

Нами предполагалось, что эффекты воздействия на ионосферу взрыва метеорита [Berngardt et al., 2013; Тертышников и др., 2013] возникают от взаимодействия ионизированного и нейтрального компонентов плазмы во взрывной волне. В работе [Зельдович, 1966] приведены результаты моделирования распределения газодинамических величин во фронте ударной волны от мощного взрыва. В указанной работе показано, что профили давления, плотности и скорости газа в ударной волне имеют как максимум, так и минимум. Следовательно, для более точного моделирования прохождения волны от взрыва необходимо учитывать, что вслед за зоной сжатия могла двигаться зона с пониженной концентрацией.

Для более точного описания прохождения взрывной волны было промоделировано распространение радиоволны в присутствии неоднородности N-типа, описываемого формулой (5). Результаты влияния на прохождение радиоволны гауссовой неоднородности и неоднородности N-типа со схожими параметрами приведены на рис. 8. Существенным различием двух диаграмм мощности является значительное усиление третьего трека. В течение первых 15 мин своего существования данный трек по мощности превосходит даже главный максимум. Трассировка показывает, что причиной этого является эффект двойной фокусировки, приведенный на рис. 9. Штриховыми линиями на рис. 9 показано положение двух зон неоднородности с положительным и отрицательным изменением электронной концентрации. Видно, что в формировании данного трека принимают участие две группы лучей: одна отражается в зоне разрежения, а другая – в зоне сжатия.

Двухскачковое распространение

В эксперименте эффекты прохождения ударной волны наблюдались в интервале дальностей 1000– 3000 км с двумя явно выраженными зонами фокусировки по дальности в спокойное время. Это говорит о двухскачковом распространении радиосигнала.

Моделирование проводилось методом, схожим с описанным выше. Отличие заключалось в том, что после первого отражения от земли вес луча уменьшался в два раза и его построение продолжалось до следующего возврата на землю. Результат моделирования диаграммы ВНЗ-сигнала при двухскачко-вом распространении при наличии N-волны представлен на рис. 10. Видно, что на втором скачке количество треков больше, чем на первом. Каждому треку первого скачка могут соответствовать два трека на втором скачке. Рассмотрим, к примеру, самый ярко выраженный трек 1 на рис. 10. Одновременно с ним на втором скачке развивается трек 2, обладающий большей кажущейся скоростью. Моделирование показало, что возникновение трека 2 связано с эффектом фокусировки на первом скачке, а не на втором. Применяя к данному треку геометрический метод оценки скорости, изложенный выше, получим

4 H

V В = V TID     ^F = 4 V TID .                         (11)

H _F

Трек 3 формируется позже трека 1, и трассировка показывает, что фокусирующее воздействие происходит в точке отражения второго скачка. Таким образом, механизм формирования данного трека схож с механизмом формирования трека 1, что определяет их общее свойство – значительное увеличение амплитуды сигнала вследствие двойной фокусировки.

Оценка скорости дает следующее выражение для трека 3:

4 H   4

V _C = V _TID      = V _TID .                         (12)

3 H _F 3

При своем дальнейшем развитии треки 2 и 3 расширяются. Можно даже говорить о разделении зоны двойной фокусировки на два обычных трека с разными скоростями.

Можно заключить, что ситуация на втором скачке гораздо сложнее, чем при односкачковом распространении. Реальную и модельную ионосферу на расстояниях в несколько тысяч километров нельзя считать сферически симметричной, а эффекты, связанные с кривизной поверхности Земли, значительны. Это ухудшает точность качественной оценки скорости с помощью модели плоскослоистой ионосферы. Такая оценка дает представление только о качественном соотношении скоростей разных треков на малых расстояниях от основного трека, связанного с суточ- ным ходом. На рис. 11 представлены профили мощности ВНЗ-сигнала, полученные при моделировании.

На рис. 11, г приведена зависимость мощности сигнала в фиксированный момент времени. Видно, что на фоновом профиле (3) присутствуют два главных максимума, соответствующих первому (I) и второму (II) скачку. На другом профиле отчетливо виден максимум, соответствующий дополнительной двойной зоне фокусировки в F-слое (III).

На рис. 11, в показано изменение мощности сигнала вдоль трека (вдоль направлений 1 и 2) по мере движения неоднородности и связанной с ней зоны дополнительной фокусировки. Сравнивая данный профиль с фоновой мощностью, можно заметить, что они различаются на любой дальности примерно на 10 дБ. Это подтверждает идею о том, что трек образуется в ре- зультате локального перераспределения энергии вследствие рефракции лучей на неоднородности.

По результатам моделирования диаграммы мощности ВНЗ-сигнала при двухскачковом распространении можно сделать следующие выводы.

• 1.    Количество треков на втором скачке больше, чем на первом. Это связано с тем, что на втором скачке треки образуются вследствие фокусировок в зоне первого и второго отражения от ионосферы.

• 2.    Скорости треков на втором скачке в общем случае не совпадают со скоростями треков на первом скачке. Они могут быть как больше, так и меньше последних.

• 3.    Скорости треков на втором скачке выше скорости движения неоднородности.

Сравнение с экспериментом

Анализ экспериментальных данных, приведенных на рис. 2, показывает, что на первом скачке в сигнале отчетливо наблюдаются два трека с кажущимися скоростями 400–550 и 800 м/c. На втором скачке наблюдается не менее трех треков, из которых два совпадают по скоростям с треками первого скачка, а третий имеет кажущуюся скорость 1600 м/с. Характерные треки 400–550 и 800 м/c имеют наибольшую амплитуду, а трек 1600 м/c наблюдается слабее.

Для того чтобы оценить скорость ПИВ по кажущейся скорости треков, необходимо задать отношение высот точек отражения в F-слое и E-слое. По модели IRI-2007 это соотношение для частоты 10 МГц и при углах излучения до 45° приблизительно равно 2. Это дает набор скоростей треков, приведенный в табл. 1. Такой теоретический набор скоростей точнее всего совпадает с экспериментальным при скорости неоднородности около 400 м/с. Результаты расчета скоростей треков сведены в табл. 2.

Согласно результатам моделирования, для возмущения N-типа наиболее выраженными должны быть моды 800, 1600 и 533 м/с. Отсутствие в экспериментальных данных всего набора рассчитанных скоростей может быть связано с низкой интенсивностью

Таблица 1

Кажущиеся скорости треков (в единицах скорости ПИВ)

	Е-треки	F-треки
1 скачок	4, 4/3	2
2 скачок	8, 8/3, 8/5, 8/7	4, 4/3

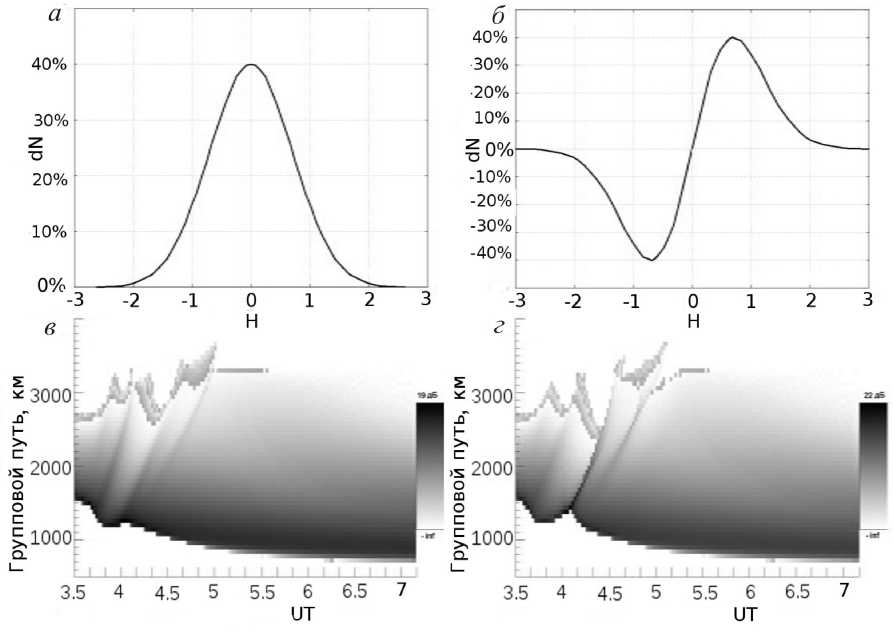
Рис. 8. Различие между профилями используемых неоднородностей и их воздействием на диаграмму мощности ВНЗ-сигнала: а - гауссово возмущение; б - возмущение N-типа; в - диаграмма мощности при наличии гауссова возмущения; г - диаграмма мощности при наличии N-волны.

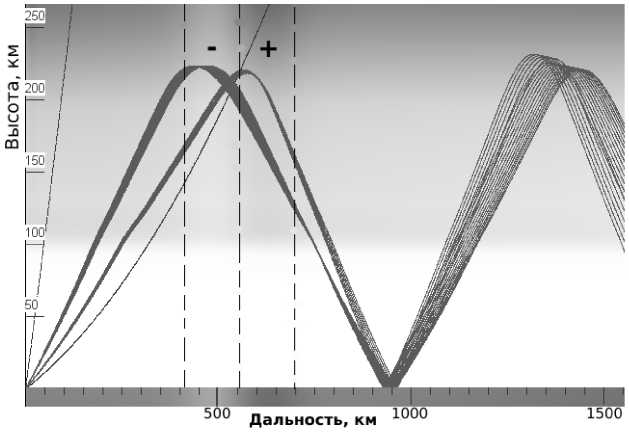
Рис . 9. Двойная фокусировка при наличии N-образного возмущения.

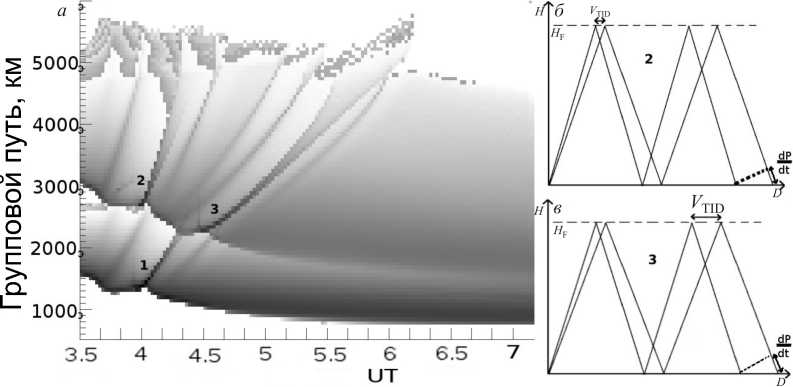
Рис . 10. Треки на диаграмме ВНЗ-сигнала при двухскачковом распространении: а - диаграмма ВНЗ-сигнала при наличии N-волны (2 скачка); б - механизм формирования трека 2 (см. панель а); в - механизм формирования трека 3 (см. панель а).

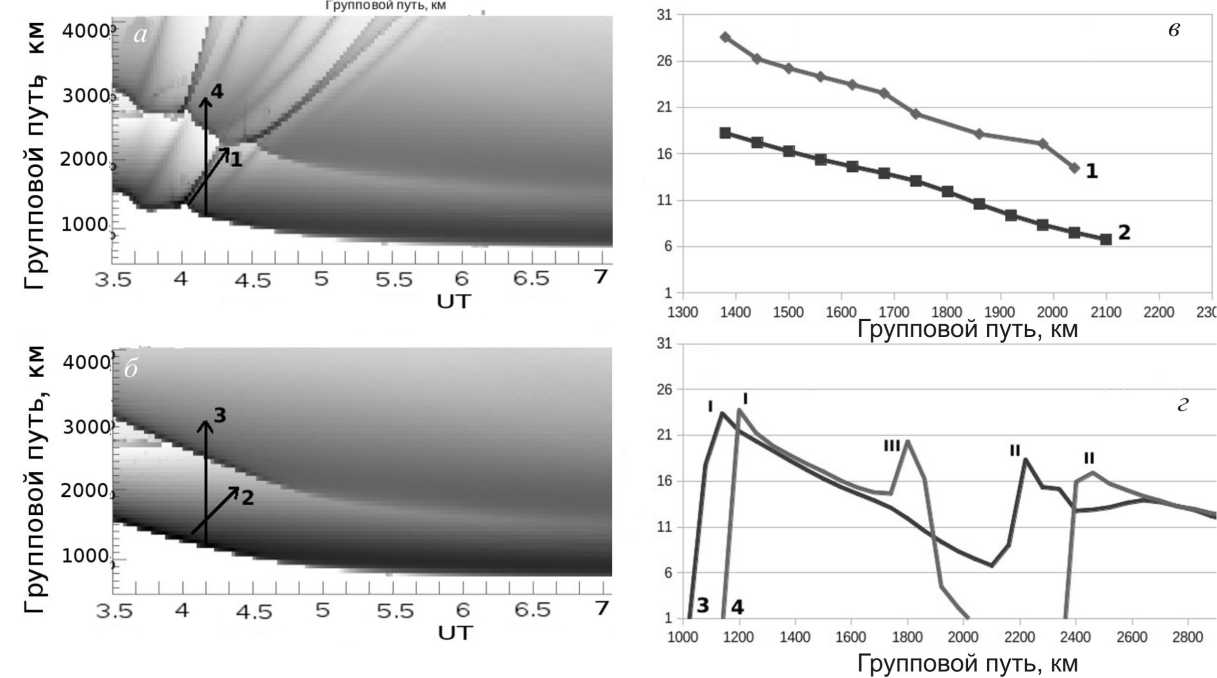
Рис . 11. Профили мощности ВНЗ-сигнала при наличии трека и без него: а – диаграмма мощности при наличии ПИВ (1 – направление трека, 4 – момент времени 4 UT); б – диаграмма мощности для фоновой ионосферы. 2 – направление трека 1, 3 – момент времени 4 UT; в – сечение мощности вдоль трека на диаграмме с возмущением (1) и вдоль того же направления на невозмущенной диаграмме (2); г – сечение мощности по дальности на 4:30 UT на диаграмме с возмущением (4) и вдоль того же направления на невозмущенной диаграмме (3). Максимумы мощности соответствуют фокусировке на границе мертвой зоны (I), фокусировке на границе 2-го скачка (II) и дополнительной зоне фокусировки – треку (III).

Таблица 2

Сравнение экспериментальных скоростей и результатов моделирования прохождения одиночного ПИВ (скорость 400 м/с)

Скорость, м/с Модель Эксперимент Е-треки F-треки 1 скачок 1600, 533 800 400–500, 800 2 скачок 3200, 1067, 640, 457 1600, 533 450–550, 750–850, 1600 треков, сформировавшихся за счет фокусировки в E-слое. Возможно, что неоднородность была локализована только в F-слое.

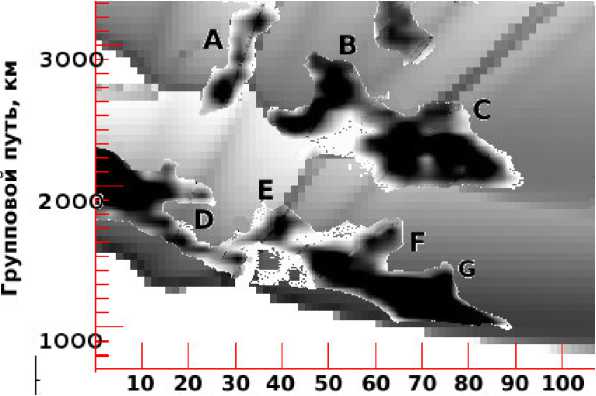
Размер неоднородности был оценен методом подгонки. Наилучшее совпадение синтезированной диаграммы ВНЗ-сигнала с экспериментальными данными соответствует размеру неоднородности H =150 км. Результат совмещения экспериментальных данных с синтезированной диаграммой представлен на рис . 12.

Совмещение показывает согласованность между моделью и экспериментом для треков, формируемых за счет двойной фокусировки в F-слое (треки A, C, E). Их скорости и групповые пути в реальных данных совпадают с рассчитанными . Время появления немного различается: задержка в модели составляет 5–10 мин.

В рамках этой модели треки F и G, не объясняемые с точки зрения неоднородности со скоростью 400 м/с, а также трек B, не согласующийся с моделью, похожи на проявления второй, более медленной неоднородности. Кроме того, задержка появления треков в модели может означать, что генерация волны происходила не в точке взрыва, а в большой области вокруг.

Для подтверждения данных предположений было проведено моделирование зон фокусировки при наличии двух неоднородностей. Скорость первой была 400 м/с. Скорость второй неоднородности варьиро- вала от 100 до 300 м/с. Для согласования времени появления треков менялись положения источников возмущений. Наилучшее соответствие между моделью и экспериментом получилось при скорости второй неоднородности 220 м/с и положении источников обеих волн в 200 км севернее предполагаемого места взрыва. Результаты такого моделирования приведены на рис. 13. Видно хорошее совпадение наклонов, групповых путей и моментов появления всех треков регистрируемых в эксперименте.

Таким образом, появление на диаграмме ВНЗ-сиг-нала радара SuperDARN EKB семи перемещающихся зон дополнительной фокусировки после падения метеорита «Челябинск» можно интерпретировать как результат прохождения через зону переднего лепестка ДН антенны радара двух радиальносимметричных возмущений N-типа (ударной волны). Характерный размер первого составлял 150 км, а скорость – порядка 400 м/с. Амплитуда неоднородностей в рамках описанной выше методике поддается лишь косвенной оценке. Она должна превышать

Время после взрыва, мин

Рис . 12. Совмещение синтезированной диаграммы ВНЗ-сигнала с экспериментальными данными (одна модельная неоднородность со скоростью 400 м/с). Буквами отмечены треки на экспериментальных данных.

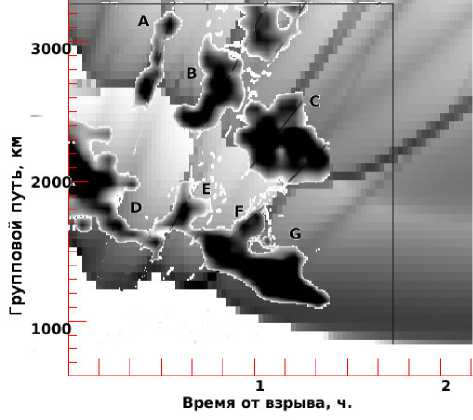
Рис . 13. Совмещение синтезированной диаграммы ВНЗ-сигнала с экспериментальными данными (две неоднородности со скоростями 400 и 220 м/с).

пороговое значение в 15 % от фоновой концентрации, необходимое для формирования трека [Stocker et al., 2000]. Характерный размер второго возмущения также составлял 100–150 км, скорость – порядка 220 м/c.

Согласно результатам моделирования, центр возмущений располагался в 200 км севернее места взрыва метеорита. Возможно, это говорит о распределенном источнике неоднородностей и качественно совпадает с остальными наблюдениями радара [Berngardt et al., 2013b]. Результаты окончательной интерпретации экспериментальных треков сведены в табл. 3.

Заключение

В данной работе предпринята попытка интерпретации экспериментальных данных, полученных на радаре SuperDARN EKB 15.02.2013 г. после взрыва и падения метеорита «Челябинск». Взрыв произошел в 200 км южнее радара. Сравнение с соседними магнитоспокойными днями показало, что после падения (03:20 UT) в принятом сигнале появляются компоненты, говорящие о наличии дополнительных перемещающихся зон фокусировки сигнала.

Таблица 3

Интерпретация экспериментальных треков

Трек	Скачок	Скорость ПИВ , м / с	Кажущаяся скорость трека , м / с	Область фокусировки
A	II	400	1600	F- слой на 1- м скачке
B	II	220	850	F- слой на 1- м скачке
C	II	400	530	F- слой на 2- м скачке
D	I	400	1600	E- слой на 1- м скачке
E	I	400	800	F- слой на 1- м скачке
F	I	220	450	F- слой на 1- м скачке
G	I	220	300	E- слой на 1- м скачке

Для объяснения данного явления была разработана методика моделирования зон фокусировки сигнала ВНЗ для радара SuperDARN. Методика основана на приближении геометрической оптики для холодной изотропной плазмы. Метод заключается в решении траекторной задачи с помощью системы характеристических уравнений с последующим подсчетом количества лучей с близкими групповыми путями от радара до возвращения на земную поверх- ность. Данная методика позволяет проводить лишь качественную оценку амплитуды сигнала ВНЗ, так как не учитывает такие факторы, как поглощение радиосигнала в ионосфере, многолучевое распространение обратно рассеянного сигнала и детальные особенности фокусировок. Однако методика достаточна для обнаружения зон фокусировки сигнала и исследования их динамики.

Результаты, полученные с помощью методики, хорошо согласуются с экспериментальными данными о суточном ходе главного максимума сигнала ВНЗ вблизи минимального группового пути. Для большего соответствия реальным условиям учитывалась ДН антенной решетки радара. В качестве фоновой ионосферы использовалась модель IRI-2007 с коррекцией по данным ионозонда «Арти».

Предполагалось, что причиной возникновения многочисленных треков обратно рассеянного сигнала на диаграмме время–дальность–интенсивность является одна или несколько перемещающихся ионосферных неоднородностей, распространяющихся радиально от места взрыва. В качестве модели неоднородности были приняты уединенная гауссова волна и волна N-типа, как более точно описывающая эффекты на фронте ударной волны.

Моделирование диаграммы ДВИ ВНЗ-сигнала при наличии ПИВ показало, что даже одна неоднородность может проявляться в виде набора треков с различными кажущимися скоростями, отличными от скорости ПИВ.

С помощью простой геометрической модели в работе получены выражения, связывающие скорости различных треков со скоростью порождающей их неоднородности. Полученные выражения объясняют ряд особенностей в динамике треков. В частности, они объясняют, почему скорости некоторых треков соотносятся, как целые числа. Полученные выражения основаны на теореме Брейта–Тьюва для плоскослоистой ионосферы и на больших групповых путях (>2000 км) некорректны.

Моделирование прохождения N-волны в целом подтвердило предыдущие выводы. Однако диаграммы мощности при наличии такого возмущения обладают одной особенностью – значительной интенсивностью одного из треков. Трассировка показала, что данная особенность вызвана двойной фокусировкой радиосигнала, являющейся основным качественным признаком присутствия N-волны.

В рамках проведенного моделирования показано, что семь дополнительных перемещающихся зон фокусировки можно интерпретировать, как распространение двух радиальных неоднородностей типа N-волны.

Результаты моделирования позволяют предположить, что первая неоднородность имела скорость около 400 м/с и характерный масштаб около 150 км. Вторая неоднородность имела характерный размер 100– 150 км и двигалась со скоростью 220 м/с. Характерная амплитуда неоднородностей составляла не менее 15 %.

Согласно результатам моделирования, на расстояниях первого скачка (500–700 км от радара) неоднородности проявлялись на высотах E-, F-слоя. На расстояниях второго скачка (1000–1500 км от радара) наблюдались лишь неоднородности на высотах F-слоя.

Работа выполнена при финансовой поддержке РФФИ (грант 11-05-00892-a) и в рамках программы

ОФН РАН IV.12.2. Авторы благодарны Кусон-скому О.А. и Григорьевой С.А. (ИГФ УрО РАН) за предоставление данных ионозонда «Арти».