Моделирование сложных динамических объектов

x(t) = J h '(t - т)u(t^dr ,

t ₀

t

x(t) = f (t -10)+Jh'(t -тU(t)dT , t0

где x(t) – выходная реакция объекта, который наблюдается в течение времени t, начиная с момента времени t 0 ; h’(t) – импульсно-переходная характеристика объекта, связанная с переходной характеристикой объекта h(t) оператором дифференцирования dh(t)/dt = h’(t); u(t) – входное воздействие на объект, которое приводит к изменению его реакции x(t); f(t) – свободная составляющая движения объекта – характеристика, описывающая поведение объекта в нестабильном начальном состоянии. Модель (1) является описанием объекта в стабильном начальном состоянии в отличие от модели (2), которая позволяет учитывать нестабильное начальное состояние объекта.

Характеристики u(t) и x(t) могут наблюдаться в ходе экспериментов с помощью разнообразных средств контроля (органы чувств пользователей, контрольно-измерительные приборы и электронные измерительные датчики). Характеристики h(t) и f(t) – временные характеристики объекта, и они являются характеристиками, идентифицирующими сам объект, то есть информация о поведении этих характеристик позволяет получить достаточное описание поведения объекта. Иными словами, чтобы построить модель объекта в определенных пользователем условиях, достаточно описать временные характеристики объекта и использовать эти описания при поиске модели.

Метод, основанный на наблюдении за поведением объекта в условиях, когда на него воздействуют при помощи специальных воздействий в тестовом режиме, является одним из наиболее используемых методов описания временных характеристик объекта. Нами рассматривается метод временных характеристик, предполагающий воздействие на объект с помощью характеристики u(t) таким образом, чтобы на выходе объекта наблюдались реакции x(t), соответствующие временным характеристикам объекта h(t) (или h’(t)) и f(t).

Для нахождения описания переходной характеристики объекта при помощи метода временных характеристик необходимо на вход объекта подать тестовый сигнал, описывающийся функцией Хэвисайда 1(t). На выходе объекта будет наблюдаться реакция, приближенно повторяющая поведение переходной характеристики объекта (рис. 1), где u(t) – характеристика, воздействующая на объект; x(t) – реакция объекта на воздействие; t 3 – время запаздывания объекта.

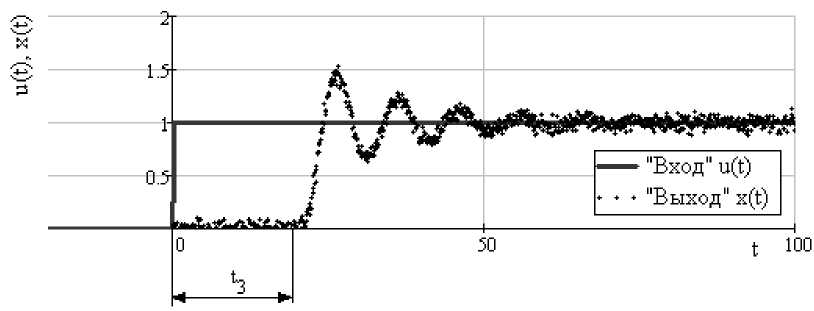
Рис. 1. Идентификация h(t)

На входе объекта подается воздействие и наблюдается запаздывающая реакция объекта на это воздействие. Можно заметить наличие случайных помех, оказывающих влияние на измерения реакции объекта. Для нахождения описания поведения свободной составляющей движения объекта необходимо привести его в интересующее нестабильное начальное состояние с последующим прекращением воздействий на объект [5]. Тогда на его выходе будет наблюдаться реакция объекта, приближенно повторяющая свободную составляющую движения объекта (рис. 2).

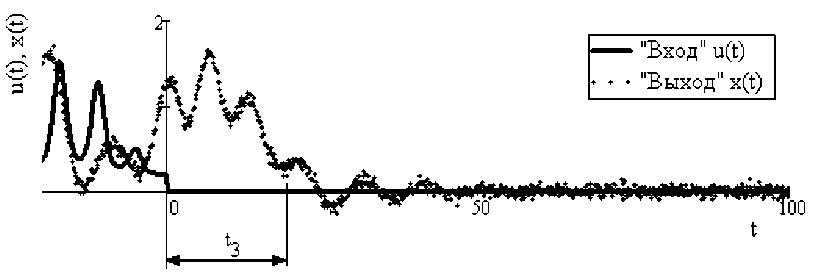
Рис. 2. Идентификация f(t)

На рисунке 2 показано, как при помощи входного воздействия u(t) в интервале времени меньше момента времени t=0 происходит направление объекта к интересующему нестабильному начальному состоянию. Далее в интервале времени с момента t=0 до t=100 воздействие на него прекращается и на выходе объекта наблюдается запаздывающая по времени на величину t 3 реакция объекта x(t), соответствующая свободной составляющей его движения, описывающая объект в этом нестабильном начальном состоянии.

Далее необходимо в условиях неопределенности восстановить поведение временной характеристики объекта по наблюдениям характеристик, полученных в результате проведения экспериментов с объектом и построить модель самого объекта. В условиях непараметрической неопределенности и ограниченности ресурсов логично использовать непараметрические оценку Надарая-Ватсона [6], оценку Пристли [7] и оценку регрессии Пристли [2].

Модифицированная оценка Пристли:

h ‘ ^(t ) = -T h y th U H f],                    (3)

s - ( c j = 1            <  c s   7                                 ⁽³⁾

где h’_s ( t ) - непараметрическая оценка импульсной переходной характеристики объекта, построенная по выборке значений переходной характеристики объекта h(t i ), в моменты времени t i ; s – объем выборки значений h(t i ); c ^hh - параметр размытости непараметрической оценки (3); H ' - колоколообразная функция непараметрической оценки.

Непараметрическая оценка Надарая-Ватсона:

■ f ⁽ t ) = -1 7tft )• H s • c i = 1

k  cs  7

,

где f ( t ) - непараметрическая оценка свободной составляющей движения объекта; f ( t ) - значение свободной составляющей движения объекта в момент времени t i ; c^f – параметр размытости непараметрической оценки.

Для построения модели выходной характеристики (5) используются оценки (3) и (4):

X-(t) = fs(t-10)+JhS(t-T)• u(T>, где t0                                                                            (5)

x_s ( t ) - непараметрическая модель реакции объекта на входное воздействие u(t).

Для оценки качества полученных моделей используется несколько критериев, например, ошибка моделирования выходной реакции объекта (6), средняя абсолютная относительная ошибка моделирования выходной реакции объекта (7):

1 ^s

Q 1 =-£ ( x ^{( t}i )^- x s ^{( t}i )) ,

s

Q 2 = ¹ 2

S i = 1

S i = 1

x ^{( t}i ^)- x s ^{( t}i ) x ⁽ t i )

• 100% , где

x ( tf ) - значение выходной характеристики объекта в момент времени t i .

Оценка качества будет происходить путем сравнения при помощи критериев (6) и (7) реакций объекта и модели на одинаковое входное воздействие. Работа метода показана на сложном динамическом объекте (8) – параметрической модели объекта, заданной дифференциальным уравнением двенадцатого порядка.

12                          11                          98

. x ( t ) + 4.598     x ( t ) + 0.926 — x ( t ) + 4.007 — x ( t ) + 3.6988 x ( t ) +

12                        11                        98

dt             dt             dtdt

+ 0.256 — x (t)+ 6.032 — x (t)+ 2.522 — x (t) + dt6             dt5

+ 0.418 d у x ( t ) + 4.152 d у x ( t ) + 0.854 — x ( t ) + 0.211 x ( t ) = u ( t - t ₃).

dt3              dt2              dt

По выражениям (3) и (4) при определенных параметрах было найдено непараметрическое описание временных характеристик объекта и построены графики непараметрических оценок (рис. 3–4).

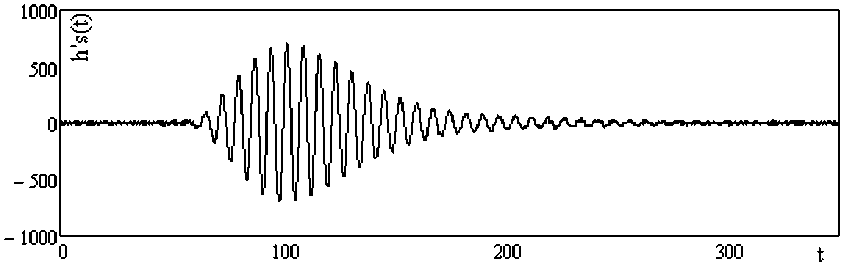
Рис. 3. Непараметрическая оценка импульсной переходной характеристики объекта

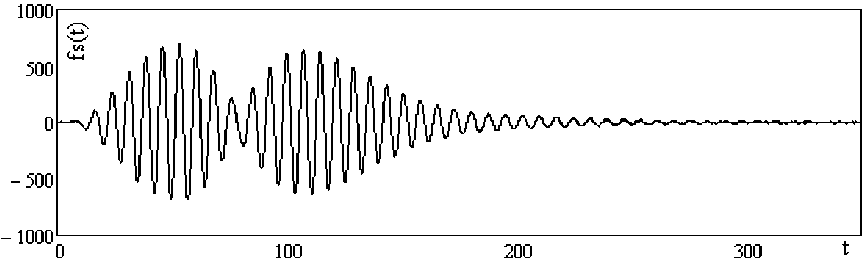
Рис. 4. Непараметрическая оценка свободной составляющей движения объекта

Построенная непараметрическая модель объекта по формуле (5) позволяет описать реакцию объекта на произвольное входное воздействие с учетом нестабильного начального состояния объекта. Сравнение полученной непараметрической модели объекта с реакцией самого объекта показано на рис. 5.

Показатели критериев качества полученной модели объекта, рассчитанные по формулам (6) и (7), составили соответственно Q1≈1000, Q2≈24 %. Данные значения показывают, что полученная модель достаточ- но сильно удалилась от значений самого объекта, однако полученный уровень качества может быть весьма удовлетворительным в условиях отсутствия априорной информации, позволяющей изучать объект исследования.

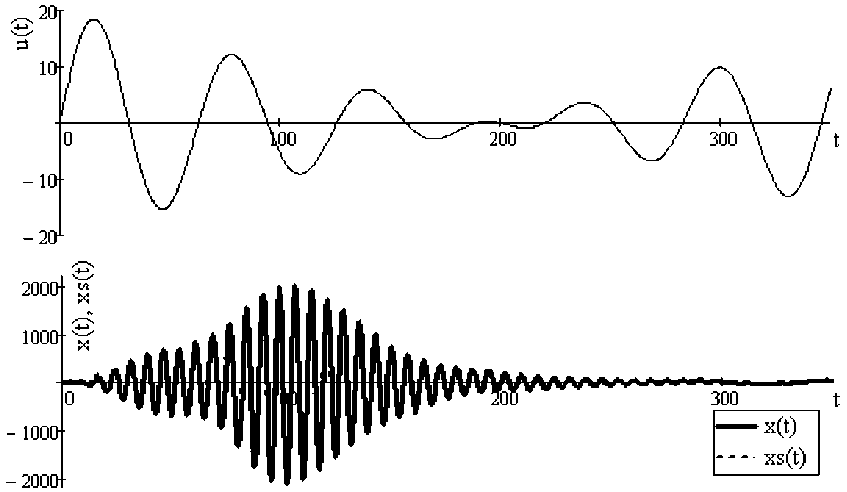
Рис. 5. Сравнение реакций объекта и модели

Заключение . Исходя из полученных результатов, можно сделать вывод о возможности описания объектов, относящихся к классу стационарных линейных динамических объектов с запаздыванием в условиях параметрической неопределенности. Непараметрические модели объектов дают возможность пользователям строить гипотезы относительно различных объектов, позволяя строить максимально точные модели независимо от ресурсов (финансовых, экономических и т.п.). Нужно отметить универсальность непараметрических моделей: они могут помочь в задачах рода поддержки принятия решений при управлении объектами.