Моделирование случайных чисел по произвольному закону распределения

Проблема моделирования случайных чисел в настоящее время приобретает все большую актуальность ввиду её широкой прикладной направленности. Существует большое количество методов моделирования случайных чисел, которое можно условно разделить на пять групп методов – на основе обратных функций, исключений (методы режекции), аппроксимации, композиции и использования предельных теорем [1 – 4]. В зависимости от исходной ситуации моделирования в прикладном отношении применяются соответствующие методы моделирования случайных чисел. Как правило, разработанные датчики моделирования случайных чисел используются в имитационном моделировании, в котором случайность учитывается непосредственно в процессе моделирования. Часто возникают ситуации, когда необходимо моделировать случайные числа по заданному произвольному закону, который представляется в эмпирическом виде, например гистограммой.

Практика показала, что сложного вида гистограмму не всегда удается аппроксимировать с помощью подходящей кривой, подчиняющейся какому-либо закону распределения, использование методов обратных функций и исключений тоже весьма проблематично ввиду сложности преобразований. Применение методов композиции весьма неудобно, т.к. необходимо делить исходную гистограмму на части, которые должны соответствовать наиболее просто и быстро имитируемым плотностям [1]. Как правило, такие части имеют довольно сложную форму, что затрудняет подбор плотностей для моделирования.

Таким образом, учитывая это, предлагается аппроксимировать исходную гистограмму совокупностью n нормальных законов, которые с целью упрощения процесса разбиения подменяются треугольными распределениями (в виде равнобедренных треугольников). Известно [2], что нормальный закон распределения довольно точно заменяется треугольным распределением, конкретно равнобедренным треугольником, для которого дисперсия

^Dx_t = “ ^/ _б ’ ° x_t = “/^ ’ 1 = U (1) где а - половина основания равнобедренного треугольника. Проведя процесс разбиения, дальше уже моделирование производится с помощью нормальных законов, как хорошо изученных и апробированных на практике. Таким образом, исходная гистограмма или исходный закон распределения заменяется взвешенной суммой нормальных законов распределения, т.е. представляется в следующем виде

/ зак (x)=E ?=i P < f t (x),        (2)

где    Pi - вероятность того, что имеет место распределение f_ (x);

f i (x^ - нормальный закон, соответствующий i -му равнобедренному треугольнику с параметрами т_Х[ , o_Xl.

Тогда для исходного распределения математическое ожидание тх = Е”=1тх1 -Pi’        (3)

где   тх.- математическое ожидание, опре деляемое по графику для i -го треугольника;

n - количество равнобедренных треугольников;

P = Si    (Si - площадь i -го треуголь- i            n z Si i = 1

ника, S i = h i - “ i , h i , “ i - высота и половина основания i -го треугольника) - вероятность того, что имеет место распределение i -й нормальный закон.

Имея величины т_х. , P i , о_х. можно моделировать случайную величину х с произвольным законом распределения.

В этом случае порядок моделирования случайной величины по произвольному закону распределения, заданному эмпирической гистограммой будет следующим.

• 1.    Эмпирическая гистограмма описывается совокупностью п равнобедренных треугольников графическим способом, сущность кото-

• рого заключается в том, что любую кривую распределения, полученную на основе статистических данных нетрудно представить в виде последовательности равнобедренных треугольников. При этом разбить таким образом, чтобы при сложении соответствующих им абсцисс получилась бы кривая, как можно ближе к реальной, исходной.

• 2.    Разыгрывается случайная величина равномерно распределенная в интервале [ 0,1 ] , который разделен в соответствии с P ( i = 1, n ) на n интервалов, определяется в какой интервал она попала, моделируется случайная величина в соответствии с i -м интервалом

• 3.    Строится расчетная гистограмма и сравнивается с первоначальной эмпирической гистограммой, при достаточной аппроксимации она принимается и используется в имитационных моделях.

X = ^ - Л - (L 6=1 T j - 3) + т х₍ , [1,3], (4)

где    Tj - случайная величина, распределен ная в интервале [0,1]. Данная случайная величина нормально распределена и соответствует i -му треугольнику. Таким образом, для получения одной реализации необходимо иметь 7 равномерно распределенных случайных величин.

Данный порядок моделирования практически реализован в вычислительной технике и представлен изобретением [6]. Цель изобретения - расширение функциональных возможностей вычислительного устройства за счет моделирования произвольных эмпирических законов распределения по нормальному закону.

Для иллюстрации предлагаемого порядка моделирования случайных чисел рассмотрим конкретный пример, в котором использовался датчик равномерно распределенных чисел, хорошо себя зарекомендовавший на практике [4,5,7,8].

Пример. В табл. 1, в качестве исходных данных, представлен вариант прогноза распределения населения России по денежным доходам до 2025г., единица измерения в интервалах - дес. тыс. руб. По исходным данным построена эмпирическая гистограмма. Необходимо на ее основе получить случайные числа и построить по ним расчетную гистограмму, достаточно точно описывающую исходную эмпирическую гистограмму.

Таблица 1 – Исходные данные для построения эмпирической гистограммы

Интервал	0,1	1,2	2,3	3,4	4,5	5,6	6,7	7,8	8,9	9,10	10,11	11,12
* p i , исх. дан.	0,06	0,123	0,245	0,21	0,123	0,088	0,07	0,042	0,018	0,0105	0,007	0,0035

Порядок моделирования случайной величины по произвольному закону распределения, заданному эмпирической гистограммой в табл.1.

Этап 1. Эмпирическая гистограмма описывается совокупностью равнобедренных треугольников графическим способом. В первом случае она описывается тремя равнобедренными треугольниками, во втором случае -семью (см. рис.1).

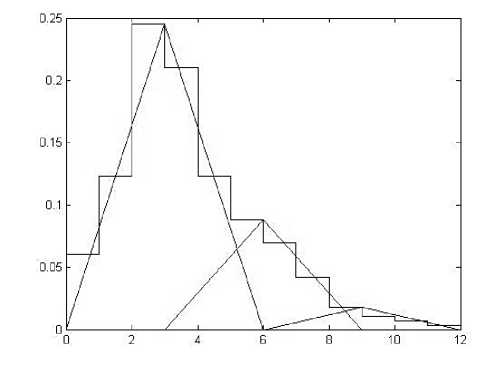
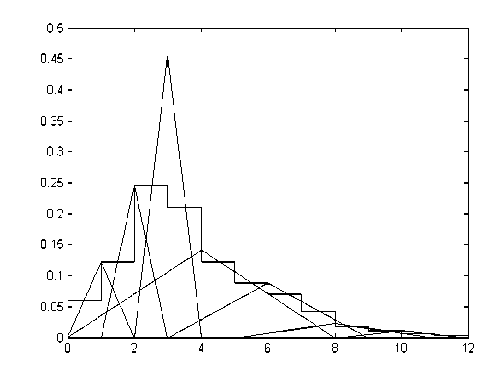
Рисунок 1 – Исходная эмпирическая гистограмма распределения и ее аппроксимация последовательностью трех и семи равнобедренных треугольников

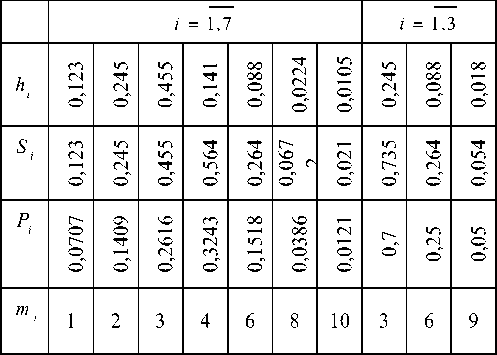
Этап 2. На основе рис.1 и зависимостей (1) – (3) определяются данные для моделирования случайной величины по зависимости (4), которые сведены в табл.2. Равномерно распределенная случайная величина r (R) определяется в соответствии с [5,7] следующим образом: P1=470001; P2=49638521; P=999563; A=P1*P2; P2=mod(A,P); R=P2/P; A=P1*P2; P2=mod(A,P); R=P2/P; и т.д.

Таблица 2 – Данные по аппроксимации исходного распределения

Этап 3. На рис.2 представлена блок схема моделирования случайных чисел для построения расчетной гистограммы.

Обозначения в соответствии с блок схемой: N – число интервалов для случайной величины (в блок схеме принято 12 интервалов, для примера); N1 – число случайных чисел, имитирующих x ; A1 – вектор размерностью N + 1 , фиксируются границы интервалов, 12 интервалов ( от 0 до 12, А1=(0 1 2 3 4 5 6 7 8 9 10 11 12)); L1 – число треугольников; А2 – вектор размерностью L1 + 1 , фиксируются границы интервалов, при L1=7 интервалов (треугольников) (A2=(0 0.0707 0.2116 0.4732 0.7975 0.9493 0.9879 1.0) в соответствии с табл.2, от 0 до 1); х _р - значение случайной величины, распределенной по произвольному закону;

N2 – вектор размерностью N , для распределения случайных величин по интервалам (в блок схеме N=12, начальное значение N2=(0 0 0 0 0 0 0 0 0 0 0 0)); BM – вектор размерностью L1 , фиксируются математические ожидания для каждого треугольника, определяются по графику; D – вектор размерностью L 1 , фиксируются среднеквадратические отклонения σ , которые рассчитываются по зависимости (1); P1=470001, P2=49638521, P=999563 – первона- чальные константы, необходимые для формирования равномерно распределенных случайных чисел.

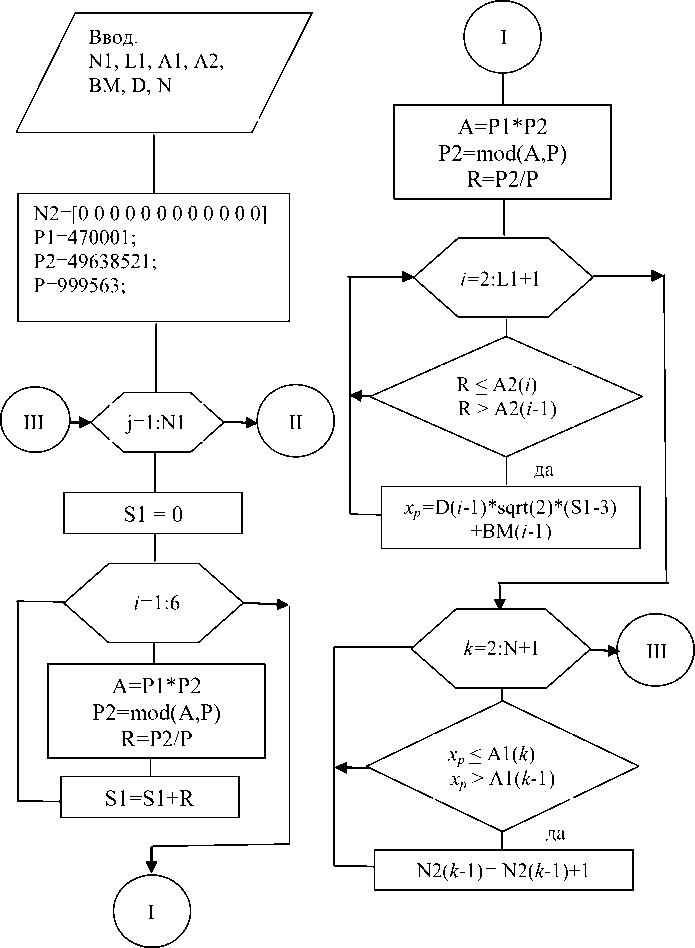
Рисунок 2 - Блок схема моделирования случайных чисел по произвольному закону распределения

Таблица 3 – Результаты моделирования по исходной эмпирической гистограмме

(для 3 и 7 треугольников)

Интервал	0,1	1,2	2,3	3,4	4,5	5,6	6,7	7,8	8,9	9,10	10,11	11,12
p i , 3 треуг., N1-50000	0.0324	0.111	0.20446	0.2116	0.15378	0.10668	0.07726	0.04616	0.02612	0.0154	0.00828	0.0023
p , 7 треуг. N1=50000	0.04308	0.131	0.2532	0.21196	0,09922	0,0992	0.07586	0.04232	0.021	0,01216	0.0064	0.00172

По данной блок схеме была разработана программа и в табл.3 сведены результаты расчетов для двух случаев, когда аппроксимация исходного распределения осуществляется тремя и семью треугольниками (нормальными законами).

На рис. 3 данные результаты представлены наглядно. Видно, что аппроксимация семью треугольниками более качественная.

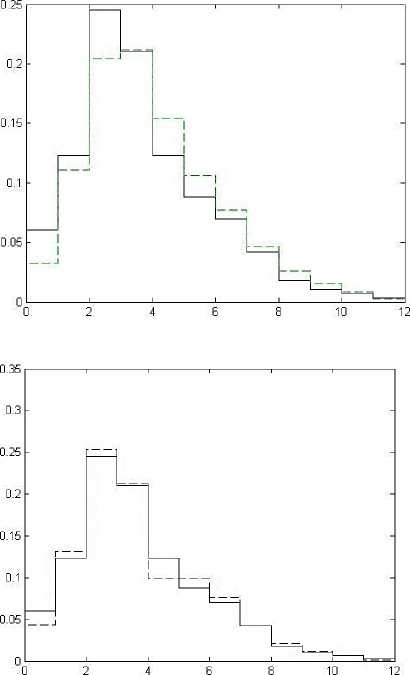
Рисунок 3 – Исходная гистограмма распределения и ее аппроксимация расчетными гистограммами для двух случаев (слева по 3 треугольникам, справа по 7)