Моделирование стационарных режимов конвективной сушки зерна в плотном подвижном слое

В настоящее время на рынке зерносушилок представлены в основном конвективные, реализующие непрерывный принцип действия в плотном подвижном слое, остающиеся наиболее эффективными, но нуждающиеся в модернизации на основе инновационных технологий и режимов. Известны построенные для решения задач автоматического управления (АУ) математические модели стационарных режимов конвективной сушки зерна в плотном подвижном слое. Во многих из них устранена излишняя для практических целей аналитичность (и соответственно антиимитационная направленность) модели А.В. Лыкова [1]. Однако большинство моделей содержит большое число переменных и неизвестных величин. Они, как правило, отражают частные законы тепло- и массообмена, не учитывают нелинейность в зависимостях и обратную зависимость теплофизических коэффициентов от основных параметров состояния процесса – влажности и температуры зерна. Эти модели, построенные для различных зерновых сушилок, осуществляющих конвективный способ в плотном подвижном слое, могут быть подразделены на два класса. Модели первого класса – эмпирические и полуэмпи-рические, имеют узкую область применения и требуют для построения проведения

трудоемких экспериментальных исследований. Модели второго класса сугубо теоретические, включают неидентифицируемые переменные коэффициенты и трудноизмеряе-мые классические физические величины. В связи с этим возникают вопросы разработки имитационно-аналитической модели, позволяющей с достаточной для решения практических задач точностью описывать динамику сушки в плотном подвижном слое, в том числе наиболее рационального осциллирующего и квазиизотермического вида изменения температуры зерна в зоне максимальной скорости влагосъема и предельных (допустимых) значений температуры сушильного агента.

У процессов сушки зерна в большинстве сушилок конвективного типа, реализующих непрерывный принцип действия (шахтные, жалюзийные, колонковые, модульные), общая термодинамическая природа, стационарные режимы могут быть описаны единой математической моделью [2‒6]. Следует абстрагироваться от постоянных конструктивных параметров, не входящих в понятие режима сушки, таких как толщина продуваемого слоя зерна, скорость продувки зерна агентом сушки, исходное состояние зерна, его предварительная подготовка перед основным процессом сушки, а также продолжительность пребывания в зоне сушки.

В результате теоретического анализа балансовых уравнений взаимосвязанного тепловлагообмена между сушильным агентом и слоем зерна построена нелинейная математическая модель, ее отличительная особенность ‒ отсутствие трудноизмеряемых (парциальное давление водяного пара) и быстроизменяемых (влагосодержание агента сушки) переменных.

Результаты исследований

Нами принято предположение о том, что возможно построение общей математической модели процессов конвективной сушки в плотном подвижном слое, которая имеет преимущества моделей обоих существующих классов и в то же время элиминирует их недостатки. Такая модель не может являться чисто аналитической; она включает модельные коэффициенты, которые, в отличие от классических физических коэффициентов, могут быть приняты постоянными и имеют имитационную направленность. На ее основе были проведены численные эксперименты. Модель удобно настраивать с учетом имеющихся экспериментальных данных, в том числе в режиме реального времени.

Результаты численного моделирования показали, что предложенная модель воспроизводит теоретически и практически возможные режимы (т.е. является гибкой и физически корректной), а также позволяет выделить рациональные и оптимальные параметры процесса. Модель обладает слабой чувствительностью к малой вариации параметров (т.е. является грубой и математически корректной). Ее простота, соответствие реальным процессам дают возможность ее применения для широкого класса задач АУ процессов сушки в конвективных сушилках с плотным подвижным слоем сушимого материала.

Для создания системы АУ процессом сушки зерна необходима математическая модель объекта [7‒10]. При анализе известных моделей, построенных для описания процессов в сушилках шахтного типа [11‒17], обнаружено: многие из них базируются на линейных соотношениях между параметрами процесса сушки при использовании переменных величин, недоступных или малодоступных измерению (таких, как парциальное давление паров в сушильном агенте и его разность с давлением насыщенного водяного пара в изменяющихся условиях по температуре агента и влажности поверхностного слоя зерна; влагосодержание сушильного агента). Разными авторами при различных условиях приведено большое количество линейных выражений для описания векторной функции плотности потока влаги, в том числе в виде разности давлений, влагосодержаний, влажностей, температур.

Однако моделирование показывает, что линейная модель сушильного процесса, основанная на использовании линейных функций плотности потока влаги, не обеспечивает совпадения с экспериментом, в связи с трудноизмеряемыми параметрами применение такой модели в задачах АУ проблематично.

Рассмотрим нелинейную модель процесса теплообмена в зерновке, на основе которой получена математическая модель процесса сушки в плотном подвижном слое. При составлении модели в качестве управляющего параметра принята температура агента сушки на входе сушильной камеры, а в качестве управляемых параметров использованы влажность и температура зерна на выходе из сушилки. Возмущающими параметрами являются начальная влажность зерна и его температура. Уравнения динамики процесса сушки в плотном подвижном слое зерна имеют вид:

^W + v ^W = —k " 0(⁽t — т), ⁽х — vт⁾)w(t, х) ,

S® ₊ v S® = r ( S^W ₊ v S^W ) ₊ a[1 —k Г^^)]^   0^     (2)

at      ax c\at      ax)      L      “\at      ax/Jv 0      v ,  //, при следующих граничных w(t, 0) = w(t), 0(t, 0) = 0(t) и начальных условиях w(0,x) = w(x),0(O,x) = 0(х), где w(t,x) = W3(t,x) - w^; Ө(t,x) = Өз(кх) - Өо;Т(кх) = Өс.а. - To - среднее текущее значение соответственно: влажности; температуры зерна; температуры сушильного агента; кw - коэффициент внутреннего тепловлагообмена; ка - эквивалентный коэффициент теплообмена между зерном и агентом сушки; α – коэффициент, характеризующий зависимость интенсивности теплообмена между зерном и агентом в функции от скорости испарения влаги; τ – время активации влагоотделения; r – удельная теплота испарения воды; c - удельная теплоемкость зерна; v - скорость перемещения зерна; t, х - временная и пространственная (текущая по высоте сушильной камеры) координаты.

Коэффициенты к w , к а , а определяются экспериментально для каждого вида зерна и зависят от типа сушилки. Уравнение для температуры сушильного агента на выходе сушилки с плотным подвижным слоем является следствием системы уравнения (1)‒(2) и поэтому не приводится. Эту систему уравнений можно записать в следующей форме:

^+raw=—kW0((t— at     ax       w

т), (х — VT))w(t, x) ,

a^ + va^ = —kwL(0((t at     ax       w c

— т), (х — VT)))(w(t,x)) +

+ а[1 + k_№(k_w0((t — т), (х — (х - VT))w(t,x))](T₀ — 0(t,x)).

В случае стационарного режима процесса сушки параметры зернового слоя зависят только от одного аргумента – пространственной координаты х , в любой фиксированной точке по высоте камеры они будут некоторыми константами.

Для стационарного режима сушки, когда входные параметры зерна и сушильного агента остаются постоянными, можно принять равными нулю производные основных переменных состояния по времени. Тогда система уравнений (3)‒(4) будет иметь вид:

a® v— = ax

—

г sW = —к " 0(х — vт)w(x) , к "^ (0(х — vт)(w(x)) + a [1 + k_a (к " 0((х

—

гт))w⁽x))] (7 0 — 0⁽х)). (6)

Сделав дополнительное предположение о постоянстве скорости зерна, заменим аргументы переменных уравнений (5)‒(6), связанные в случае установившегося режима очевидным соотношением x = vt , получим систему дифференциальных уравнений стационарного режима сушки:

;W = -k_w0(t-T)w(t) , (7)

S^+^-^Jfo-eto). (8)

Уравнение стационарного режима можно трактовать как уравнение движения элементарного объема зернового материала в синхронной системе координат. При сушке зерна этот элементарный объем имеет смысл интерпретировать как некоторую усредненную единичную зерновку.

При проведении численного эксперимента на модели (7)‒(8) часть теплофизических параметров (b = r/c) и начальные данные (wo, Өо, To) с целью упрощения были приняты в качестве констант. Основные варьируемые параметры – модельные коэффициенты, определяемые характером и особенностями внутреннего и внешнего тепло- и массообмена между зерновым слоем и агентом сушки. Запаздывающее звено математической модели имитировалось подсистемой у0 = -К(т)у0 + К(т)у1, (9) у1 = -К(т)у1 + К(т)у2, (10) у2 = -К(т)у2 + К(т)у3, (11) у3 = -К(т)у3+К(т)у5, (12)

которой заменяем в общей системе уравнения, содержащие запаздывающий аргумент.

K = 1,5, у 0(т) = 0(t) , у(5)(t - т) = 0(t - т) . (13)

Дополнив эту систему основными уравнениями, описывающими динамику изменения основных переменных состояния процесса, получили операционную модель у4 = -kwУ0 у4, (14)

у5 = 1,12у4 + а(1 - к_ау4)(50 - у5), (15) позволяющую изучать стационарные режимы конвективной сушки зерна в плотном подвижном слое. Последнее уравнение в этой системе описывает закон изменения температуры зерна в процессе сушки, а уравнение (14) – закон изменения его влажности.

При определенных соотношениях между скоростью агента сушки, его температурой и теплофизическими параметрами зерна, наряду с обычным режимом, когда температура зерна монотонно нарастает (рис. а , кривая 1 ), в сушилках с плотным подвижным слоем были отмечены режимы, при которых на температурной кривой нагрева зерна в области максимальной скорости испарения влаги наблюдается колебание (рис. а , кривые 2 , 3 ), стабилизация (рис. б , кривая 4 ), провал (рис. б , кривые 5 , 6 ).

Вопрос изучения модели связан также с вопросом нахождениия оптимальных режимов процесса сушки: минимум расхода энергии на единицу испаренной влаги (или на единицу условной испаренной влаги), минимум расхода топлива (или условного топлива) на единицу (тонну или плановую тонну) просушенного зерна; скорость ее с учетом ограничений на температуру сушильного агента и температуру зерна, а при сушке семенного зерна – с учетом ограничений на максимальный вла-госъем за один проход.

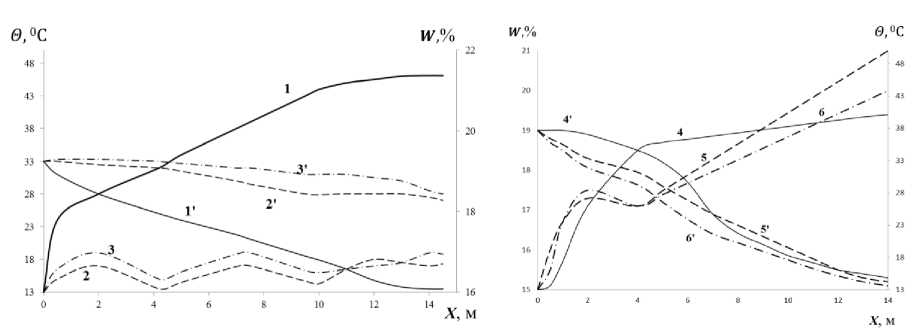
а)

б)

Зависимость температуры зерна 0 (кривые 1-6) и влажности w (1’-6‘) по высоте сушильной камеры х в сушилках с плотным подвижным слоем: а ) с колебательным «ходом» температурной кривой; б ) с «провалом» температурной кривой

В качестве исходных данных моделей с учетом нормирования линейных размеров сушильной камеры приняты следующие параметры: y 40 = 20; y 50 = 0; T 0 = 50; v = 0,7. Нулевой (средний) уровень варьируемых параметров был выбран: k w = 0,06; α = 0,40; k α = 0,90. При имитационном моделировании и проведении численных экспериментов шаг этих параметров был принят равным 0,02; 0,05; 0,10, соответственно. В модели коэффициенты теплообмена и массообмена являются переменными величинами

a(w, Ө) = I(w, Ө; k w , a , k_a , т ) = (a (J(w, Ө; k w ; т )-k_a ^W ),

e(w, Ө; k_w; т ) = k_w0w.

Это отвечает результатам экспериментальных исследований.

Моделирование выявило возможные рациональные режимы сушки. Теоретически многократно обсуждалась возможность колебательного характера сушки материалов (и что особенно важно, в наиболее эффективных импульсных, осциллирующих и так называемых изотермических режимах), по крайней мере, в зоне максимальной ее скорости ^W [18-22]. Они имеют место при трехфазном векторном управлении с дифференциацией в нисходящем режиме в трехзонной сушильной камере с переменной толщиной продуваемого слоя.

Механизм такого процесса объясняется следующим образом: при определенном соотношении параметров материала накопленное в нем тепло приводит к интенсивному испарению. Если поток тепла, поступающего от сушильного агента, не компенсирует дефицит тепла, требуемого на испарение, материал несколько охлаждается и скорость испарения падает, это ведет к нагреву сушимого материала. Если условия испарения влаги выполняются, возможен выход на следующую волну; если условия колебания отсутствуют, продолжается монотонный рост температуры. Важно в первой зоне довести температуру зерна до значений, близких, но не превышающих предельно допустимое (с запасом, не меньшим точности регулирования), а во второй, уменьшив количество теплоты до уровня, обеспечивающего компенсацию расхода тепла на испарение влаги, поддерживать эту температуру. Третья зона (многофункциональная) может быть использована для доведения конечных значений влажности и температуры зерна до кондиционных значений с подачей холодного или нагретого агента. Монотонность процесса может нарушаться при коэффициентах теплообмена и скоростях сушильного агента, недостаточных для компенсации тепла уносимого испарившейся влагой в зерне в зоне максимальной скорости влагосъема.

Режим колебательного процесса сушки возникает при малых значениях коэффициентов интенсивности теплообмена k α ( k α = 0,2) или малых значениях теплообмена внутреннего тепловлагопереноса k w ( k w = 0,032). Это характерно для материалов c большой собственной теплоемкостью или для тех случаев, когда материал отдает часть тепла на нагрев других предметов, не участвующих в испарении.

Все режимы сушки могут быть получены на данной модели, даже в предположении постоянства коэффициента тепловлагообмена. Отметим характерную особенность решения модели в этом случае: у начального участка кривой нагрева зерна высокий темп, что не соответствует экспериментально наблюдаемым закономерностям сушки в зерносушилках шахтного типа и других типов камер с плотным подвижным слоем.

Очевидно, что каждый из режимов обладает различными показателями по критериям эффективности процесса сушки зерна и что существуют (как правило, отличающиеся между собой) оптимальные режимы (с точки зрения отдельных критериев или некоторой интегральной целевой функции) [23‒25].

Таким образом, предлагаемая модель полностью воспроизводит практически реализуемые и теоретически возможные режимы сушки, в том числе:

• ‒    режим с монотонным ростом температуры сушимого материала;

• ‒    режим с практически горизонтальным участком кривой температуры в зоне постоянной скорости испарения влаги;

• ‒    режим с провалом кривой температуры материала в зоне максимальной скорости испарения;

• ‒    колебательный ход кривой температуры материала в зоне постоянной скорости испарения влаги.

Рассматриваемая модель имеет достаточную простоту, а также грубость и гибкость. Она с полной качественной и хорошей количественной точностью воспроизводит процесс сушки. Обладает слабой чувствительностью вариации параметров, т.е. корректна. У нее широкая область применения, распространяющаяся на все зерносушилки, реализующие конвективный способ сушки в плотном подвижном слое, ее коэффициенты постоянны и легко идентифицируемы, а переменные состояния измеряемы с приемлемой для практических целей точностью.

Наличие пяти параметров в исходной модели (1)‒(2) с учетом качественного соответствия ее реальным процессам позволяет идентифицировать параметры полной системы на основе стационарного процесса (7)‒(8). Точность идентификации ограничивается не видом математической модели (в частности, числом и локацией ее модельных коэффициентов), а точностью и степенью дискретизации и отделимости измеряемых переменных состояния процесса сушки зерна в сушильной камере.

Простота данной модели и одновременно нелинейность, учет переменного характера физических коэффициентов модельными постоянными коэффициентами, ее адекватность реальным процессам дают возможность ее применения и основанного на ней подхода к моделированию для широкого класса задач автоматизации и оптимизации процессов сушки зерна.

Среди большого разнообразия возможных стационарных режимов процесса конвективной сушки зерна в плотном подвижном слое наиболее эффективны двух- и трехэтапные режимы, реализуемые в инновационных сушильных установках [26‒28]. Это связано с наличием трех фаз протекания процесса конвективной сушки зерна и позволяет устранить существующие противоречия между процессом (нелинейным, с распределенными параметрами), режимом управления и конструкцией зерносушилки (недопускающими векторное управление и предполагающими скалярное управление линейной системой со сосредоточенными параметрами). В каждой из трех сушильных зон дифференцируются конструктивные (толщина слоя) и режимные (температура агента сушки) параметры. Их согласованные значения оптимизируются на основе идентифицируемой математической модели.

Наличие выявленных свойств модели позволяет идентифицировать ее для разных видов зерна и типов зерносушилок, использующих конвективный способ сушки в плотном подвижном слое. Использование настраиваемых коэффициентов позволило упростить модель и повысить ее интерпретируемость, а также упростить процедуры алгоритмизации, давая возможность функциональной и параметрической идентификации модели. Ее простота связана с возможностью задать постоянными теплофизические характеристики, включенные в модель, и их изменение описать при помощи предложенных нелинейных функций

J(x) = k_w0(x - vt)w(x),/(x) = a [1 + k_a (k_w0((x - vt))w(x))] (Т 0 - 0(x)) (18) и коэффициентов k_w , a , k_a , т . Результаты моделирования позволили раскрыть характерный вид оптимальных режимов и подтвердили эффективность дифференцированных режимов в позонных зерносушилках и возможность квазиизотермического процесса во второй, наиболее протяженной зоне сушильной камеры, где осуществляется вторая (основная) фаза сушки.

Заключение

Построенная модель полностью воспроизводит практически реализуемые и теоретически возможные режимы сушки, обладает достаточной простотой, а также грубостью и гибкостью. С полной качественной и хорошей количественной точностью воспроизводит процесс сушки, что связано с ее структурой, термодинамической основой и идентифицируемостью модельных коэффициентов. Модель обладает слабой чувствительностью вариации параметров. Степень ее адекватности ограничена точностью начальных и текущих данных, их количеством и точностью измерений.

Данный подход к моделированию применим для широкого класса задач автоматизации и оптимизации процессов сушки зерна. Представлены рациональные и оптимальные параметры процесса сушки зерна. Показано, что в общем случае дифференцированные режимы сушки обладают преимуществом перед ступенчатыми, а ступенчатые перед равномерными (одноступенчатыми); у квазиизотермических (осциллирующих) преимущество перед традиционными неизотермическими; у импульсных реверсивных преимущество перед непрерывными односторонними.

Krasnoyarsk State Agrarian University, Krasnoyarsk

MODELING OF STATIONARY REGIMES OF CONVECTIVE GRAIN DRYING IN THE DENSE MOBILE LAYER

Work is performed in case of a financial support of Regional public autonomous institution “Krasnoyarsk Regional Fund of Support of Scientific and Scientific and Technical Activities ” (the supplementary agreement No. 09/16 of 02.06.2016)