Моделирование структуризации в адгезионном слое при создании многослойных объектов

Создание многослойных объектов путем ламинирования (Laminated Object Manufacturing или Sheet Lamination — LOM), относится к широко распространенным технологиям получения трехмерных изделий. Если изначально способ LOM использовался в изготовлении бумаги с защитным слоем, то в настоящее время эта технология применяется в таких сферах, как строительство, микроэлектроника, производство керамических/стеклокерамических объектов, различного рода композитов, органических изделий, склеивание фольг и в другом. Разнообразие областей внедрения LOM объясняется простотой осуществления и высокой скоростью выхода конечного продукта [1, 2].

В процессе создания трехмерного объекта способом LOM условно выделяются 4 этапа. Первый этап заключается в разработке с помощью системы автоматизированного проектирования модели будущего изделия — CAD модели, которая загружается в промышленный компьютер установки.

На втором этапе происходит подача на рабочую платформу установки листового материала с предварительно нанесенным между листами адгезионным слоем. Третий этап включает вырезание лазером контуров изготовляемого изделия. На четвертом этапе полученные листы подлежат послойному склеиванию посредством прокатывания нагретого ролла, а излишки расходных материалов — удалению.

Несмотря на значительные преимущества технологии, существуют проблемы, которые требуют решения. Способ LOM хорошо работает при соединении листов бумаги, пластика, органики. Высокая точность производства и простота склеивания однотипных материалов достигается за счет варьирования толщин их слоев в пределах от 0,05 до 0,1 мм. Однако замена одного из них, к примеру, на металл, отражается как увеличение толщины листа от 0,2 до 0,5 мм, что приводит к усложнению операции склеивания. Тогда, например, как в работе [3], для соединения металлических фольг используют двухступенчатый процесс. Сначала с помощью LOM придают листам металлической фольги необходимую форму, затем слои соединяют диффузионной сваркой. Еще одной проблемой соединения фольг является зубчатость границ металлических функциональных изделий сложной формы и большой объем обрезаемого материала. Данная проблема подробно рассмотрена в статье [4], в которой проведено теоретическое исследование по улучшению точности технологии LOM для производства изделий сложной формы. Авторы получили результаты, позволяющие влиять на погрешность производства за счет изменения поверхности среза лишнего материала посредством лазера. Так, для изделия в форме четверти цилиндра радиусом 100 мм и высотой 50 мм при толщине слоя в 1 мм удалось в 3,7 раза уменьшить отходы. В работе [5] для создания функционально-градиентного материала Ti–C–Ni осуществлен двухступенчатый технологический процесс. На первом этапе для соединения листов металлов применялась технология LOM, на втором — синтез горением. Благодаря этому авторы достигли непрерывного распределения связки Ti+C+Ni в объеме материала, что привело к однородному распределению свойств.

В соединительных составах при получении слоистых изделий способом LOM могут наблюдаться физико-химические процессы. Так, традиционно используемые для этой цели органические материалы и клеи разного состава претерпевают фазовые переходы и структурные изменения, способствующие образованию соединения. Поскольку процесс синтеза в адгезионном слое сопровождается явлениями физической природы разнонаправленного действия и с отличающимися пространственными и временными масштабами, то возможно появление критических условий, которые необходимы для его начала. Непосредственное наблюдение за структурными изменениями не представляется возможным. Для изучения и объяснения закономерностей, приводящих к формированию многослойных объектов, требуется прибегать к математическому моделированию. Прототипами моделей процессов, сопровождающих LOM, могут быть модели макрокинетики, в которых описываются режимы экзотермических реакций в слоевых системах. Например, в [6] рассматривается горение в системе, состоящей из чередующихся слоев горючего и инертной прослойки заданных толщин. Реакция в горючем протекает без участия газовой фазы, теплофизические свойства слоев неизменны. Предложена условная корреляция горения в модельной системе и в реальном гетерогенном материале. В работе [7] обсуждается роль конкурирующих механизмов переноса тепла — теплопроводности и излучения — в установлении разных режимов горения.

В [8, 9] исследуются особенности распространения экзотермической реакции между слоями инертного материала. Температура горения в модели регулируется за счет разбавления экзотермического состава инертными частицами, на нагрев которых идет часть тепла. Публикации [10–12] связаны с изучением формирования соединения разнородных материалов; анализируется влияние различия теплофизических свойств всех материалов на скорость горения и максимальную температуру во фронте.

Работа [13] посвящена горению в двухслойных системах, состоящих из низкоплавких металлов или сплавов и высокоэнергетических смесей с образованием пористых продуктов. В результате между слоями образуется слой композитного материала, толщина которого определяется глубиной проникновения расплава в пористый продукт горения. Горение слоевого пакета исследуется в [14]. Одни слои представляют собой высококалорийные составы, вторые — инертные либо низкокалорийные составы. Для обеих систем авторы выявили стационарные и нестационарные режимы горения, показали возможность перехода между режимами. В работе [15] анализируется горение слоевой композиции из двух пористых реакционных слоев, разделенных слоем легкоплавкого инертного вещества. Фронт горения перемещается в направлении, перпендикулярном положению слоев, показана возможность сопутствующего процесса пропитки пористого слоя расплавом.

В [16] предложена модель распространения экзотермической химической реакции в слое между двумя инертными материалами с разными свойствами при условии, что по внешней поверхности перемещается источник тепла конечных размеров. Фактически моделируется синтез соединительного состава непосредственно в процессе ламинирования. Представлены результаты расчетов, показывающие существование разных режимов процесса.

Следует заметить, что экзотермически реагирующие составы соединительных слоев пока слабо распространены в технологии LOM. В большинстве случаев используются составы, которые в процессе нагрева, совмещенного с механическим нагружением, претерпевают некоторые структурные изменения (структурные фазовые переходы, полимеризацию, рекристаллизацию, уплотнение и другое), не сопровождающиеся значительными тепловыми эффектами. При описании процесса на макроуровне и для всех подобных ему удобно применять единый параметр. Авторами данной работы не найден в литературе общепринятый термин. Одни и те же явления разные исследователи называют «структурными превращениями», «структуризацией», «структурированием», «структурообразованием», «формированием структуры», а соответствующую величину — «степенью структуризации», «степенью структурирования», «степенью превращения или глубиной превращения».

В рамках предлагаемой вниманию читателя статьи для макроскопического описания процесса будем использовать термины «структуризация» и «степень структуризации», чтобы отличать ее от степени превращения в реакциях, сопровождающихся значительными тепловыми эффектами. Впервые формулируется термокинетическая модель структуризации в адгезионном слое, приводящая к изменению свойств этого слоя. В зависимости от температуры регулирующего склеивание ролла, скорости его движения и давления прижатия реализуются разные условия для формирования структуры. Площадь пятна контакта и максимальные напряжения следуют из решения известной контактной задачи. Таким образом, цель работы состоит в изучении роли управляющих факторов, таких как давление прижатия ролла, его температура и скорость его движения, в установлении стационарного или квазистационарного режима ламинирирования.

• 2.    Постановка задачи

Рассмотрим трехслойную систему, состоящую из двух инертных слоев и адгезионного слоя между ними, как показано на рисунке 1. Для соединения слоев А и В по поверхности верхнего слоя с постоянной скоростью и движется ролл радиуса R_o , нагретый до температуры T_s . Ширина ролла совпадает

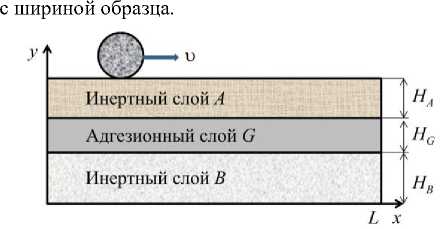
Рис. 1. Схема задачи

Примем, что толщины слоев малы, а скорости распространения механических возмущений много больше скорости распространения тепла. Поэтому в первом приближении, аналогично [16], можно ограничиться двумерной термокинетической постановкой задачи, в которой параметры ролла определяют размер подвижного источника тепла и максимальные действующие напряжения. Возможными краевыми механическими эффектами при x = 0 и x = L пренебрегаем.

Максимальное напряжение в зоне контакта, возникающее при приложении давления к роллу, движущемуся по поверхности инертного слоя А , равняется [17]:

о„ = ц max

p

2Ro(91 + 62) ,

а полуширина площадки контакта находится по формуле:

S = Ц42PR (61 + 62 ) .

Здесь: ц = 0,798 — размерный коэффициент, следующий из приближенного решения контактной задачи; p — давление прижатия ролла; 6 _к = ( 1 -v _к)[ E k — комплексы, включающие коэффициенты Пуассона v_k и модули упругости Е_к контактирующих тел ( к = 1,2). Именно это напряжение передается на весь образец и оказывает влияние на процессы в адгезионном слое.

В результате определение поля температуры сводится к решению двумерной сопряженной задачи теплопроводности, включающей уравнения теплопроводности для инертных слоев:

'а г   д ² Т к )

_v д x ^{2 +} д у ² J ^,

д Т .

ck Р к     = Х к д t где индекс к описывает инертные слои А и В, ек — теплоемкость, р^ — плотность, Тк — температура, Хк — коэффициент теплопроводности, x и у — пространственные координаты, t — время.

В зависимости от вида соединяемых между собой материалов и ожидаемых свойств ламинированного композита берутся разные адгезионные материалы (порошки, пленки, органические и неорганические материалы), в которых могут наблюдаться химические реакции и разнообразные структурные изменения: фазовые переходы, полимеризация, рекристаллизация, уплотнение и другое. Положим, что химические реакции, приводящие к изменению состава, в адгезионном слое отсутствуют, однако возможна перестройка структуры его материала. Чтобы отделить этот процесс от вызываемого собственно химической реакцией, назовем его структуризацией. Этим модель в данной работе отличается от используемой в [16].

Согласно работам [18–21], процесс изменения структуры может быть представлен в виде обратимой реакции, не сопровождающейся сколько-нибудь значительными тепловыми эффектами. Тогда степень структурных превращений a будет следовать из кинетического уравнения:

da

— = w 2 ^— w i , dt

где w2 = к2 (1 - a), w = ka — соответственно скорости прямой и обратной реакции. В неизотермических условиях k , k — функции температуры. Все перечисленные выше процессы являются термически активируемыми, их скорости зависят от температуры по закону Аррениуса. В случае реакций, протекающих с участием твердых веществ, закон для скорости реакции может быть более сложным [22, 23]. Активировать реакцию можно не только за счет изменения температуры (внутренней энергии), но и совершив работу [24]. Этому отвечает еще один экспоненциальный закон. Например, в химии твердого тела большое распространение получила формула Эйринга–Козмана w~ k0 exp

Г E— аV*

( RT

где V * — активационный объем, ст — действующее напряжение, к₀ — предэкспоненциальный множитель, E — энергия активации, R — универсальная газовая постоянная, T — температура. При записи этого уравнения подразумевается, что действующие напряжения облегчают переход через энергетический барьер, но не влияют на его высоту [25].

Заметим, что детальная схема превращений (стадийность реакций), как правило, не ясна или является сложной и неоднозначной. Скорость превращений в твердой фазе определяют не только химические реакции, но и многочисленные физические процессы, которые сложны для непосредственного изучения; протекают эти процессы на микроуровне (на уровне отдельных частиц, зерен, границ раздела). Самый простой выход в данной ситуации — это использовать такое макроскопическое понятие как степень превращения [22–25]. Именно так поступают в макрокинетике [26]. В законах для скорости реакций появляется кинетическая функция, вид которой зависит от процессов на микроуровне. Кроме того, практически любая реакция потенциально может идти как в прямом, так и в обратном направлении. Это верно в отношении всех перечисленных процессов. В соответствии с данными эксперимента [3–5, 27, 28], структура за единичный проход ролла полностью не формируется, что частично связано с обратимостью этого процесса, а частично — с действием конкурирующих факторов. Сочетание температуры и механической нагрузки позволяет контролировать процесс. В результате для скоростей прямого и обратного процессов запишем:

w 1 = к 1 а = k₁₀a exp I a^

max

—

E 1

RT G

,

w 2 = ^к 2 ( 1 ^{— а} ) = ^к 20 ( 1 ^{— а} ) exp I ^а 2 CT ma _X

E 2

RT G

Здесь: к ₀, к₂₀ — предэкспоненты; aj, а₂ — коэффициенты чувствительности скоростей реакции к действующему напряжению; E , E — энергия активации прямой и обратной стадий структуризации; R — универсальная газовая постоянная; T — температура адгезионного слоя; a — степень структурных превращений (степень структуризации).

Заметим, что даже в относительно изученных процессах конкретные кинетические параметры требуют специального экспериментального определения, что в цели данной работы не входит. Однако известно, что структуризация может приводить к изменению свойств [18–21]. Так, согласно работе [29], коэффициент теплопроводности аморфных и частично закристаллизовавшихся полимеров может быть различным. Коэффициенты теплопроводности картона разной структуры отличаются почти на порядок [30]. Таков же порядок расхождения коэффициентов теплопроводности сухого и утрамбованного грунта. В рассматриваемой в данной работе задаче наибольший интерес представляет именно теплопроводность, так как от соотношения теплопроводностей слоев зависит степень неоднородности распределения температуры и, как результат, характер структуризации. Предположим, что структуризация вызовет изменение коэффициента теплопроводности адгезионного слоя: XG = X2 (1 - a) + X1 а , где X2 и X, — коэффициенты теплопроводности неструктурированного (индекс 2) и полностью структурированного (1) адгезионных слоев. Возможно использование только линейной зависимости от состава (или правила смеси), поскольку конкретная структура на микроуровне в рамках данной модели не известна. Итак, существует либо реагент (1 - а), либо продукт (а), либо их смесь. Тогда уравнение теплопроводности для адгезионного слоя примет вид:

5Tg _. a cGPG ~    X2 д at      ax

1 IX1

1 + a —

(X 2

—

1 llaTG Lx a

1 I I----- I + X-> —

) \ ax I     ay

, IX,  Jiat

1 + а I — — 1 I I —G

(X2 )J aу

.

Примем условия адиабатичности на торцах и в плоскости у = 0 :

x = 0, x = L :      X _k 'T = 0    ( k = B , G , A ) ,

a x

У = 0:

кА = 0.

B д y

На границах раздела слоев положим выполнение условий идеального теплового контакта:

^X B” = ( ^X 2 ^{( 1 —} a ^{) + X} 1 a ) “X G ,    T B = T G ,

at     at.

y = HB + HG :   (X2 (1 — a)+X1aLx"- = XA “X- ,   TG = TA .

На поверхности слоя А , вследствие движения горячего ролла, присутствует подвижный источник тепла ограниченного размера 2 s . Для у = H_B + H_G + H_A имеют место условия:

- в зоне соприкосновения ролла со слоем А, то есть при и t + x ₀ — s <  x < и t + x ₀ + s

T A = T s ;                                               (10)

- вне зоны контакта, то есть при x < иt + x0 — s и x > иt + x0 + s aTA=0. aу

В начальный момент времени образец имеет температуру Т _о, слой G неструктурированный ( а = 0).

Модель содержит физические параметры, которые можно найти в литературе, получить из экспериментов или рассчитать на основе химической термодинамики, однако точность их определения будет невысокой. В подобных случаях в макрокинетике (то есть при изучении химических процессов с учетом сопутствующих физических стадий) используется анализ моделей в безразмерных переменных, что позволяет установить наиболее существенные для процесса параметры, выявить критерии, характеризующие процесс. Поэтому представим систему (1)–(11) в безразмерном виде.

Анализ задачи в безразмерных переменных выгоден еще и потому, что модель, представленная в статье, охватывает общие свойства разных технологий, в которых свойства материалов, размеры изделий, скорость и температура ролла значительно различаются. Размеры объектов, которые создаются в технологиях LOM, самые разные. Возможность быстрого получения деталей больших размеров (до нескольких метров) относится к одним из преимуществ данной технологии. Размеры ролла и давление прижатия также варьируются в довольно широких пределах и зависят как от параметров производственного оборудования, так и от применяемых материалов. Например, в [31], где представлена упрощенная теплофизическая модель, данные для ролла были следующими: s = 9 мм; и = 25,4 мм/с; Т = 91 °C, и теплофизические свойства керамики. В [32] технологические параметры варьировались, задавались нагрузки: p = 12, 25, 40, 51 кг; температуры ролла: T_s = 120, 170, 220, 270, 320 °C; скорости: и = 5, 10, 20, 40 мм/с. Полагалось, что стальные листы соединяются посредством акрилового клея.

С помощью термопар осуществлялись измерения температуры в разных слоях, которые позволили построить типичную кривую «температура–время» для задач с подвижными источниками тепла. В [33] на основе полуаналитической модели рассчитывались размер пятна контакта, температура и напряжения в окрестности ролла при его параметрах: T_s = 200 °C; и = 1,27 см/с. В статье указана и теплопроводность 0,501 Вт/(мК). В целом процедура изготовления ламинатов из металлических листов подобна процедуре создания ламинированной бумаги. В технологии используются органические материалы, полимеры, керамика, спрессованные порошковые материалы и другие. Получают ламинаты не только при соединении разнородных материалов, но и при постепенном изменении состава и свойств слоев.

Поэтому для нахождения наиболее общих результатов и параметрического исследования модели перейдем к безразмерным переменным:

Т -Т

9, = T-T- El , ^k RT ^{2   2}

A=

^A   H_G ’

ⁿ= i?

t                     ^{— 1}       I ^E1

т = —, t = (L0) exp —- a    20        RT aS

где t — характерное время протекания прямой реакции структуризации. После обезразмеривания модель принимает вид:

_K ^ ₌ K k_ f d ² 0 k   9_X

Ck дт     8 I d^ ²     dn ²

( k = A, B),

99r

G дт

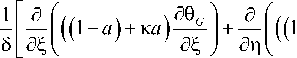
a    Ад9с Y a ) + Ka)----I dn J

—

da = ( 1 — a ) Ф 2 ( 9 , о ) — у a Ф 1 ( 9 , ст ) . d т

Здесь

_Y = k l ^,

ф, ( 9 , о ) = exp I а,ст +

^{8 + 9} G ) 1 + P9 g J ,

ф₂ ( 9 , о ) = exp I а₂ст +

9 G

1 + P9 G

Запишем граничные условия:

A = 0,

^ = L :     d9i = 0       ( dA n = 0 :     d9B = 0 ;

dn

( k = A , G , B ) ;

П=А _B :

„  59„         x x59r

Ku—B =( (1 — a ) + K a)--- ,

" ^B dn    ^{((     )     )} dn

9_S = 9_g ;

BG

П= ^{1 + A} B ^:

d9G

((1 — a) + Ka) ^

n = ^{1 + А} B ^+A A :

de A = 0, 5n

9 A

если

= 0, если

д9 a

K XA     , dn

®^{т +} A) ^— ^ A

9 G =9 A ;

^<®т + ^ 0

^{— A} A    и

<^<ют + ^ 0 + A A ;

^>®т + ^ о + A A ;

начальные условия ( т = 0):

a = 0;

9 k =—9 a ,

где k = B , G , A .

Задача (12)–(21) включает следующие безразмерные величины:

– геометрические параметры (длину образца, высоты инертных слоев А и В ):

L = LH g , A A = H a/ H g , A B = H b/ H g ;

высота слоя G в безразмерных переменных становится единичной (А_с = 1);

– параметры, связанные с теплофизическими свойствами материалов слоев и структурными превращениями:

V — ck ^P k K Ck ^—       ,

c G ^P G

RT ^e— •

X.        E, - E

к — —L ,   £ — —---1

x2        -T

0,

,

^k-

K X k   ,

^X G

T T e

RT S ^{2   2 ,}

• Y= , k ₂₀

( k — B , A),

g _ ^HG^CG P G ~ X2 t_a

,

a1 — a p*,    ta

• — ^a2 p * ;

– характеристики технологической установки, при этом принято:

П —   ,

p _*

^A \П ,    CT —aVn ,    ^ — x^-,

HG

и t„ ю — —-,

H G

^HG ²

2 ц ² - о ( 0 1 +0 ₂ ) .

В процессе исследования значения безразмерных величин варьировались в достаточно широких пределах. Иллюстрации представлены для ограниченного набора их значений.

• 3.    Метод численного исследования

• 4.    Результаты работы

Для численной реализации задачи (12)–(21) использовались неявная разностная схема, метод расщепления по координатам и линейная прогонка [34]. Проверка сходимости численного решения проводилась на решении задачи для подвижного ролла при параметрах: в — 0,1; у — 0,2; 0₀ — 5 ; 5 — 50;

L — 24; ю — 0,01; П — 1;   £ — 0,87 ; к — 0,1; a,—а,— 0; К_г .— К_г „— K, — К„ — 1. Как видно

’         7   7          7         7    7         7 7     12’     CA     CB     XA     XB из таблицы 1, при изменении шагов по пространству и времени результаты вычисления температуры в точках наблюдения расходятся не более чем на 2%, что подтверждает хорошую сходимость выбранного алгоритма.

Таблица 1. Проверка сходимости численного решения при ю — 0,01 , П — 1, т — 1200

Шаг по времени (Ат)	Шаг по пространству ( А^ —Ап )	Значение температуры образца в точках наблюдения
		0 ( 0, Н / 2 )	0 ( L / 4, Н / 2 )	0 ( L 3, Н / 2 )	0 ( L / 2, Н / 2 )
1,00	0,02	–2,8144	–2,7724	–2,7381	–2,6287
	0,01	–2,8087	–2,7668	–2,7326	–2,6232
	0,005	–2,8073	–2,7655	–2,7313	–2,6221
	0,0025	–2,8065	–2,7648	–2,7306	–2,6215
0,50	0,02	–2,7980	–2,7558	–2,7213	–2,6114
	0,01	–2,7931	–2,7511	–2,7166	–2,6067
	0,005	–2.7900	–2,7480	–2,7136	–2,6037
	0,0025	–2,7891	–2,7472	–2,7128	–2,6030
0,25	0,02	–2,7844	–2,7420	–2,7075	–2,5971
	0,01	–2,7815	–2,7393	–2,7047	–2,5944
	0,005	–2,7787	–2,7366	–2,7020	–2,5917
	0,0025	–2,7770	–2,7349	–2,7003	–2,5900

Характер распределения температуры и степени структурных превращений в образце зависит от скорости движения ролла и давления прижатия, а также от соотношения теплофизических свойств материалов. Необходимые для получения хороших адгезионных соединений температуры и скорости могут отличаться значительно, а свойства слоев — на целый порядок. Все расчеты, результаты которых представлены далее на рисунках 2-5, выполнены при ю — 0,01 , П — 1 , у — 0,5 , 5 — 5 , £ — 0,87 , aj — a₂ — 0. Границы адгезионного слоя нанесены пунктирными линиями. В случае подвижного ролла (центр пятна контакта находится в точке с переменной координатой ^ ), распределение температуры (см. Рис. 2)

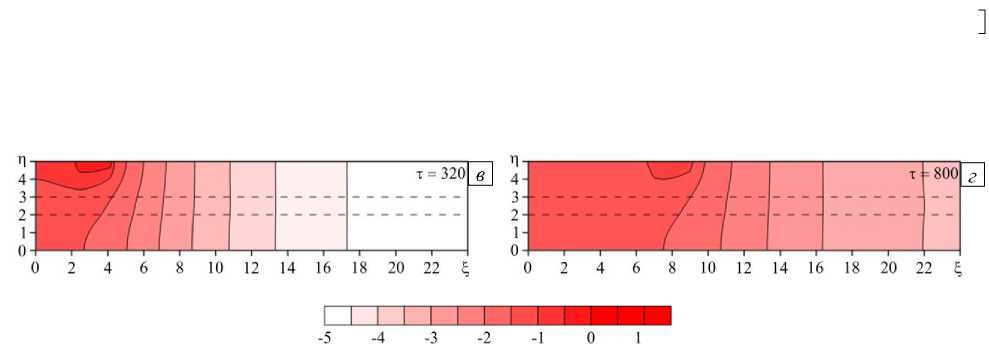
Рис. 2. Двумерные распределения температуры в образце в разные моменты времени т при

K = K = K = K = 1;

CA     CB     кА     к B

центр пятна контакта находится в точке с координатой § : 0,2 ( а ); 0,8 ( б ); 3,2 ( в ); 8,0 ( г )

неоднородно даже при одинаковых теплофизических свойствах слоев А и B . При высокой скорости движения ролла образец может не успеть прогреться до температуры, необходимой для начала структуризации.

По мере продвижения ролла образец постепенно нагревается. Неоднородность прогрева хорошо видна на начальной стадии движения ролла. Например, на границах адгезионного слоя фиксируется различие значений температуры вплоть до времени т = 1280 — момента прихода ролла в точку £ = 12,8 (см. Рис. 3 а ). Аналогичная ситуация наблюдается со степенью структурных превращений до т = 320 (Рис. 3 б ); в этот момент ролл находится в точке ^ = 3,2 .

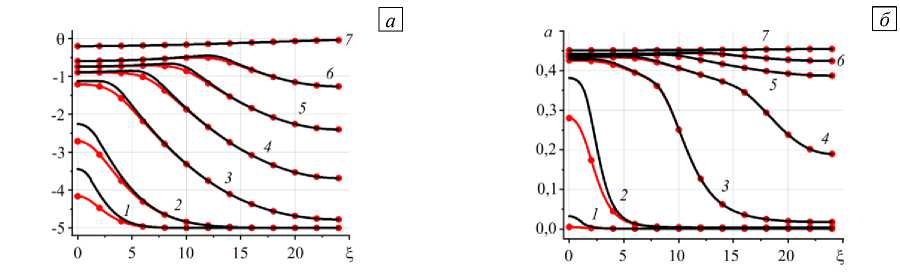
Рис. 3. Распределение температуры ( а ) и степени структурных превращений ( б ) на верхней (сплошные линии) и нижней (линии с точками) границах адгезионного слоя в разные моменты времени т : 20 (кривая 1 ), 80 ( 2 ), 320 ( 3 ), 640 ( 4 ), 960 ( 5 ), 1280 ( 6) , 2400 ( 7 )

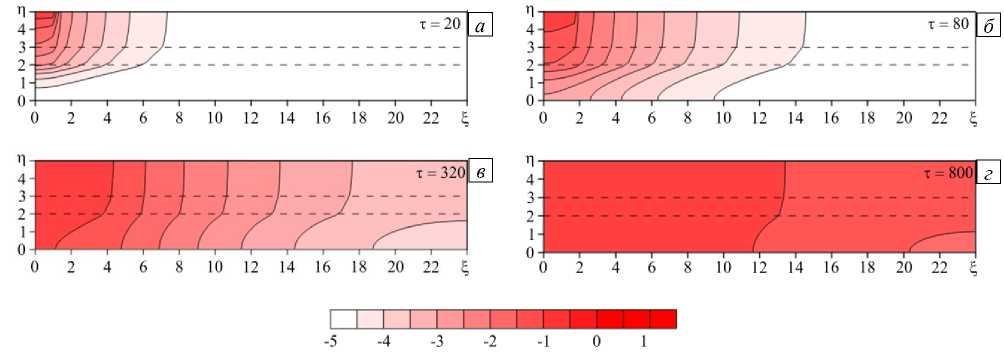
Рис. 4. Двумерные распределения температуры в образце в разные моменты времени т при K_o = K_cв = 1 , K_XA = 5 , K_xв = 0,2 ;

центр пятна контакта находится в точке с координатой ^ : 0,2 ( а ); 0,8 ( б ); 3,2 ( в ); 8,0 ( г )

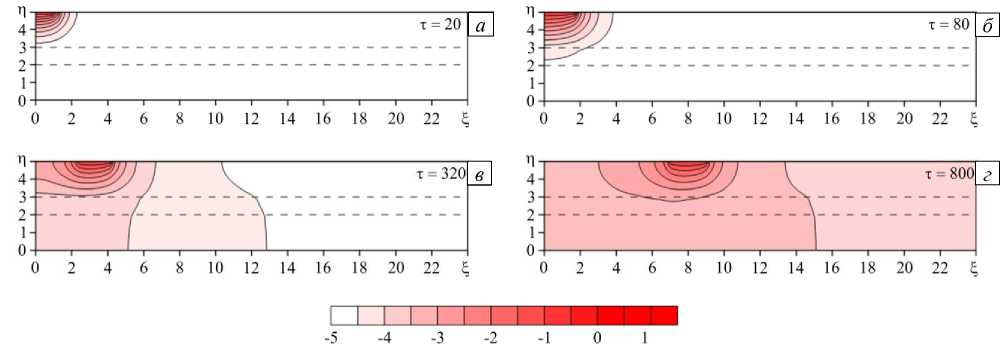
Рис. 5. Двумерные распределения температуры в образце в разные моменты времени т при K_a = K_{c s} = 1 , K _M = 0,2 , K, _B = 5 ;

центр пятна контакта находится в точке с координатой ^ : 0,2 ( а ); 0,8 ( б ); 3,2 ( в ); 8,0 ( г )

На рисунках 4, 5 показаны распределения температуры при различных соотношениях коэффициентов теплопроводности слоев А и В .С увеличением коэффициента теплопроводности слоя А (Рис. 4) наблюдается более быстрый прогрев этого слоя перед роллом, но величина температуры уменьшается. В противоположной ситуации (Рис. 5) температура в слое клея изменяется значительно медленнее.

Представленные примеры не позволяют однозначно судить об установлении режима распространения тепла — стационарного или квазистационарного, и процесса структуризации. Если рассматривается образец конечных размеров, то для определения теплового режима более удобным оказывается исследование поведения среднеинтегрального значения степени структурных превращений I_a и средней по толщине адгезионного слоя степени структуризации ( а ) :

. 1+Д в Л L             Л

7   / I f a (^n) d ^ I d П ’

L Д в 1 0           J

1+Д в

(а) = J a(7n)dП.

Дв

Стационарному режиму будет соответствовать практически постоянная максимальная температура и неизменяющаяся среднеинтегральная степень структурных превращений:

0

j+i max

—

j max

0

< 10 ^{— 5},

max

V a + ¹ — Va

I a^j

< 10 ^{— 5},

где j — номер слоя по времени (то есть в числителях стоит изменение величины за один шаг по времени).

На время установления стационарного режима влияют параметры модели. На рисунке 6 показано, что с течением времени оба условия установления выполняются с точностью 10^-5, но по-разному для различных наборов параметров. Например, при параметрах у = 0,5 , ® = 0,00048 , П = 1 , е = 0,87 с ростом § увеличивается время установления стационарного режима: при 5 = 1 стационарный режим возникает практически мгновенно, а при 5 = 100 время установления стационарного состояния составляет 35000 (вследствие увеличения неоднородности в распределении температуры).

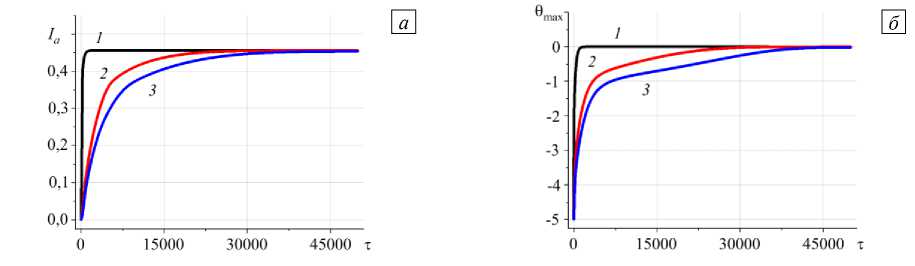
Рис. 6. Зависимость среднеинтегральной степени структурных превращений ( а ) и максимальной температуры ( б ) от времени при y = 0,5 , ш = 0,00048 , П = 1, s = 0,87 , а =а₂ = 0 и различных значениях 5 : 1 (кривая 1 ); 50 ( 2 ); 100 ( 3 )

Большие значения δ соответствуют большим толщинам слоя клея, что тождественно уменьшению характерного теплового масштаба, равного размеру области прогрева, которая может сформироваться за характерное время.

Результаты вычислений, представленные на рисунках 2–6, получены без учета влияния на кинетику коэффициентов чувствительности скоростей реакции структуризации к действующим напряжениям. Из рисунка 7 а видно значительное влияние на степень структуризации величин α и α : с возрастанием значения α увеличивается среднеинтегральная степень структурных превращений. Аналогичная ситуация, как и ожидалось, повторяется в характере зависимости распределения средней по толщине степени превращения (Рис. 7 б ).

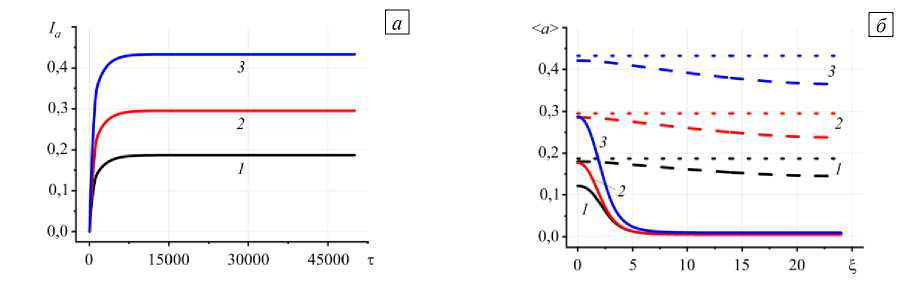
Рис. 7. Зависимость среднеинтегральной степени структурных превращений от времени ( а ) в разные моменты времени τ : 100 (кривая 1 ), 2500 ( 2 ), 15000 ( 3 ); распределение средней степени превращения по толщине слоя клея вдоль координаты ξ ( б ) в разные моменты времени τ : 100 (сплошные линии), 2500 (штриховые), 15000 (пунктирные) при γ= 1 , δ= 10 , ω = 0, 00048 , Π= 1 , ε= 0,87 и различных сочетаниях значений безразмерных коэффициентов чувствительности скоростей реакции к напряжению α : α = 5 , α = 0, 2 (кривые 1 ); α = 0, 2 , α = 0, 2 ( 2 ); α = 0, 2 , α = 5 ( 3 )

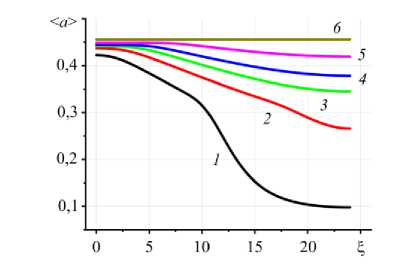
Рис. 8. Зависимость средней по толщине адгезионного слоя степени структуризации при γ= 0, 5 , ω= 0, 00048 , Π= 1 , ε= 0,87 , α = α = 0 в разные моменты времени τ : 2500 (кривая 1 ); 5000 ( 2 ); 7500 ( 3 ); 10000 ( 4 ); 15000 ( 5 ); 50000 ( 6 )

Примеры зависимостей времени установления

Степень структуризации в адгезионном слое ко времени окончания процесса ламинирования является функцией всех параметров. Так, с увеличением скорости движения ролла сокращается поступление тепла и, соответственно, уменьшается величина среднеинтегральной степени структурных превращений. По этой же причине укорачивается время до момента окончания технологического процесса (Рис. 8). Слой оказывается структурированным лишь частично, а накопившегося тепла недостаточно для увеличения степени структуризации. На рост давления прижатия ролла значение среднеинтегральной степени структурных превращений реагирует слабо (что вполне объяснимо расширением площади контакта и, следовательно, ростом температуры в слое клея), но заметно короче становится время установления стационарного значения I .

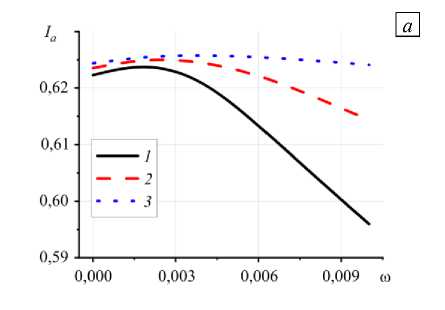
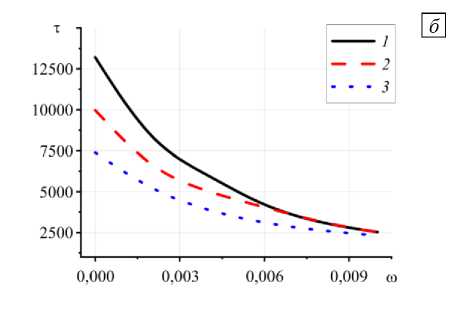
стационарного значения I от параметров модели представлены на рисунках 9–12. С увеличением скорости движения ролла быстрее прогревается верхний слой образца, однако тепло может не достичь адгезионного слоя, что уменьшает степень структурных превращений и, соответственно, удлиняет время установления стационарного значения I a (см. Рис. 9). Из рисунка 10 видно, что увеличение давления прижатия ролла ведет к уменьшению времени установления стационарного значения I независимо от значения δ .

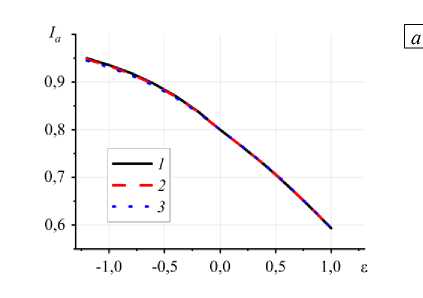
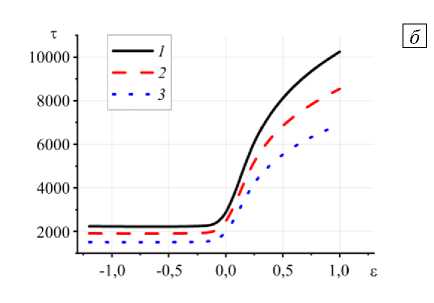
В отличие от технологических характеристик изменение кинетических параметров ε и γ приводит к значительному изменению величины среднеинтегральной степени структурных превращений к моменту установления квазистационарного режима. Рост ε влечет за собой увеличение φ (см. (14)) и, соответственно, ускорение обратной реакции структуризации, хотя начаться она может позже; в результате этого значительно уменьшается среднеинтегральная степень структурных превращений, что показано на рисунке 11 а . Время установления стационарного значения I резко возрастает.

0,62

0,61 -

0,60 ■

0,000

0,003

0,006

0,009 со

а

Рис. 9.

12500-

10000- х

2500-

0,000

0,003

0,006

0,009 со

б

Зависимость среднеинтегральной степени структурных превращений ( а ) и времени установления стационарного

значения I  (б) от скорости движения ролла при y = 1, 6 = 10 , 8 = 0,87 , прижатия ролла П : 0,1 (кривая 1); 1 (2); 10 (3)

а

0,625 -

0,624 -

0,623 -

а = а₂ = 0 и различных значениях давления

б

— 2

Л

0,9

0,8

0,7

0,6

а

Рис. 11.

Зависимость среднеинтегральной

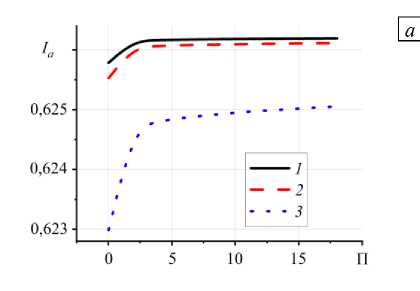
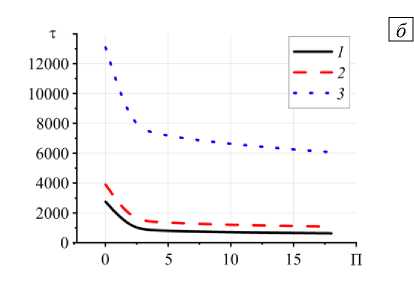
Рис. 10. Зависимость среднеинтегральной степени структурных превращений ( а ) и времени установления стационарного значения I_Q ( б ) от давления прижатия ролла при y = 1 , ю = 0,00048 , 8 = 0,87 , а₁=а₂= 0 и различных значениях 6 : 0,5 (кривая 1 ); 1 ( 2 ); 10 ( 3 )

1,0 е

-------1

— — 2 • - - 3

б степени структурных превращений (а) и времени установления стационарного ю = 0,00048 , а, =а2 = 0 и различных значениях давления прижатия ролла П :

значения I_Q ( б ) от 8 при y= 1 , 6 = 10 , 0,1 (кривая 1 ); 1 ( 2 ); 10 ( 3 )

а

10000-

2,0 у

б

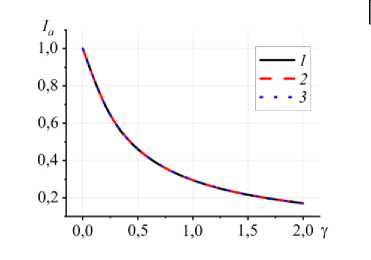
Рис. 12. Зависимость от кинетических свойств среднеинтегральной степени структурных превращений ( а ) и времени установления стационарного значения I_Q ( б ) при 6 = 1, ю = 0,00048 , 8 = 0,87 , а, = а₂ = 0 и различных значениях давления прижатия ролла П : 0,1 (кривая 1 ); 1 ( 2 ); 10 ( 3 )

Величина I a существенно уменьшается с увеличением параметра γ , при этом время, необходимое для установления его стационарного значения, резко возрастает до γ= 0, 45 (см. Рис. 12), что опять-таки связано с ускорением обратной стадии структуризации.

• 5.    Заключение

Таким образом, в работе предложена теплофизическая модель процесса структуризации в адгезионном слое. Наличие у структуризации прямой и обратной стадий и зависимость скоростей их протекания как от температуры, так и от напряжений приводит к тому, что к окончанию движения ролла возможна неполная структуризация. Это говорит о необходимости подбора технологических условий для получения заданной структуры адгезионного слоя. Соотношения теплофизических свойств инертных слоев и их геометрические размеры также влияют на характер распределения температуры и степени структурных превращений. При одинаковых значениях I я , достигаемых при разных наборах параметров, времена окончания реакции структуризации могут сильно различаться. Показано, что учет прямой и обратной стадий, а также зависимости скоростей стадий от температуры и напряжений позволяет обнаружить и неполноту превращения, и выход на квазистационарный режим, и влияние на процесс внешних управляющих факторов. Надеемся, что описанные закономерности побудят экспериментаторов контролировать не только механические свойства изготавливаемых ламинатов, но и величины, характеризующие сам процесс создания объектов (время начала превращений, размер области, где идут структурные превращения, время окончания структуризации и другие), что важно для идентификации входящих в модель параметров.

Заметим, что в настоящей работе роль отдельных параметров специально не изучалась. И то, что коэффициенты чувствительности скоростей стадий сказываются на величине степени структурных превращений, продемонстрировано лишь на примере. Отношение коэффициентов теплопроводности структурированного ( λ ) и неструктурированного ( λ ) материалов κ = λ λ в расчетах кривых, приведенных на всех рисунках, было фиксированным и равнялось 0,1, то есть принималось, что коэффициенты теплопроводности после и до структуризации отличаются на порядок. Однако отдельные результаты, не представленные в статье, показали, что увеличение κ приводит к более однородному распределению температуры в адгезионном слое и ускорению оттока тепла в нижний слой. Подобные выводы будут представлять интерес применительно к конкретным материалам, для которых кинетика структуризации будет изучаться.

О неполноте превращений в структуре и ее зависимости от условий эксперимента имеется информация в экспериментальных работах [27, 28]. Величина скорости ω= 0,01 означает, что за время t a ролл проходит расстояние, в 100 раз меньшее, чем толщина слоя адгезива. Это может обеспечить его почти однородный прогрев по толщине, однако наличие теплопроводности и потери тепла в нижний слой ситуацию усложняют. Величина δ= 50 означает, что толщина слоя адгезива в 50 раз превышает то расстояние, на которое слой прогревается за счет теплопроводности за то же время t a . В статье этот параметр варьировался в широких пределах. Увеличение скорости ролла требует, как и в экспериментальных исследованиях, повышения его температуры для того, чтобы стартовал процесс структуризации. При изменении соотношений между масштабами динамика процесса, что очевидно, изменится. Однако использованные в статье критерии будут полезными в любом случае.

Определение входящих в модель кинетических параметров, а также характера зависимости свойств от степени структуризации на основе данных вычислительных экспериментов — предмет дальнейших исследований. Предложенную модель можно усовершенствовать за счет учета температурной зависимости свойств, а также за счет явной постановки и решения связанной задачи нахождения напряженно-деформированного состояния объекта, создаваемого LOM способом.

Исследование выполнено при финансовой поддержке РФФИ в рамках научного проекта № 20-33-90016.