Моделирование структуры и процессов разрушения зернистых композитов

Выявление и исследование закономерностей неупругого деформирования структурно-неоднородных сред является важной и актуальной задачей. Информация об особенностях механического поведения и влиянии структурных параметров на процессы накопления повреждений рассматривается как основа для развития методов расчёта ответственных конструкций [1 –3] . В ряде случаев увеличение деформационного ресурса и способности сопротивляться внешним нагрузкам при наличии трещин или дефектов у деталей и элементов конструкций связано с учётом закритической стадии неупругого деформирования [4–10].

В экспериментальных исследованиях закритическая стадия деформирования наблюдается при кинематических условиях нагружения образцов (в условиях же «мягкого» нагружения, когда осуществляется контроль усилия, закритическая стадия на диаграммах деформирования не проявляется). Ряд особенностей неупругого деформирования на стадии разупрочнения при динамических воздействиях обнаружен в [11]. В настоящей работе рассматриваются некоторые закономерности закритической стадии деформирования, обусловленные процессами структурного разрушения зернистых композитов.

Одним из актуальных направлений установления закономерностей механического поведения зернистых композитов является разработка алгоритмов и программных комплексов для синтеза новых моделей структуры [12, 13] и для численного моделирования процессов неупругого деформирования, накопления повреждений и макроразрушения [14]. Использование современных вычислительных систем делает возможным учёт в модели таких параметров как пористость среды, форма, относительный размер и ориентация структурных элементов.

Так, в [15–17] вычислительные эксперименты по моделированию механического поведения зернистых структурно-неоднородных сред при различных видах нагружения послужили основой для выявления закономерностей процессов неупругого деформирования и разрушения, связанных с параметрами структуры. Полученные данные могут быть использованы при создании новых материалов с заданным комплексом физико-механических свойств или для разработки рекомендаций по изменению структуры с целью улучшения эффективных деформационных и прочностных свойств материалов.

Для обнаружения связей структурных параметров с закономерностями неупругого деформирования ранее в [18] авторами предложен оригинальный алгоритм синтеза микроструктур зернистых композитов, имитирующий пошаговый рост эллипсоидов (в плоском случае — эллипсов). Для описания формы и относительных размеров зёрен используются соответствующие коэффициенты k_f = ab и k_r = a _max I a min , где a и b — большая и малая полуоси эллипсоидов соответственно; a _max и a _min — размеры больших полуосей наибольшего и наименьшего эллипсоидов соответственно. На рисунке 1 показаны модели плоских зернистых структур с разным числом зёрен (элементов структуры).

Рис. 1. Модели зернистых структур с разным числом зёрен: 100 ( а ); 250 ( б ); 500 ( в )

Для описания процессов неупругого деформирования и разрушения структурно-неоднородных сред используем двухуровневую структурно-феноменологическую модель механики композитов [19]. Полагаем, что рассматриваемое тело состоит из множества элементов структуры, которые разделены границами и имеют различные механические свойства. При этом характерные размеры структурных элементов превосходят молекулярно-кинетические размеры.

Исследование механического поведения элементов структуры проведём на основе моделей механики деформируемого твёрдого тела, применимых для элементарных микрообъёмов dv , размеры которых много меньше размеров неоднородностей. Макроскопические процессы деформирования и разрушения неоднородных материалов опишем моделями сплошной среды для макрообъёмов dV . Объём dV должен содержать достаточно большое число структурных элементов, чтобы быть представительным и обладать эффективными свойствами.

Считаем, что все уравнения, справедливые для однородных сплошных сред, описывают механическое поведение материалов и на структурном уровне. Уравнения равновесия, записанные без учёта массовых сил, имеют вид:

° j r ) = °.

Компоненты тензора структурных деформаций e j связаны с компонентами тензора структурных перемещений и, соотношениями Коши:

еу (r ) = ( u  ^ r) + uj, i (r)) А

Определяющие соотношения микронеоднородной среды представим в виде:

° j ⁽ r ) = C ijkl ⁽ r ) ( I klmn ^-Q klmn ⁽ a kl ( r ) , ^e , ^j nL ) ) ^e mn ⁽ r ) .

В уравнениях (1)-(3) приняты обозначения: c j — компоненты тензора напряжений; r — радиус-вектор с компонентами r j ; e — тензор деформаций; C ijkl — компоненты тензора упругих модулей; I klmn = ( ⁵ km ⁵ ln ^{+ 5} kn ⁵ Im )/ ^{2 —} компоненты единичного тензора, где 5 kn ^— символ Кронекера; ^Q kim„ ^— компоненты тензора повреждённости четвёртого ранга; j ^{( Y} _c r — прочностные константы материала;

m akl (r) = X aki)k(i)(r) — коэффициенты, содержащие информацию о структуре и свойствах среды i=1

и являющиеся либо периодическими, либо случайными однородными функциями, определяются

с использованием индикаторных функций k ^{( 1} ) ( r ) : k ^{( 1} ) ( r ) = | область, занимаемая i -м компонентом, m — число компонентов

V r е V i ,

V r й V i , композита.

m

^ k ^{( 1} ) ( r ) = 1, где V i

i =1

Запятая в нижнем индексе

означает дифференцирование по координате.

Для полноты постановки краевой задачи механики деформирования и разрушения структурнонеоднородных сред систему уравнений (1)-(3) необходимо дополнить граничными условиями. Уравнения

u i ( ^r Ж =V j-

записанные для границы тела S , соответствуют условиям макрооднородной деформации. В рамках рассматриваемой постановки могут быть учтены явления когезионного и адгезионного разрушения на уровне элементов структуры. В данной работе ограничимся моделированием внутризёренного разрушения по нескольким механизмам и представим совокупность критериев разрушения [10] для элементов структуры в виде: f m ( j £1 ),..., j £ ^{7 l} ) > j -^т2 , f m — некоторые универсальные функции, у — число независимых инвариантов тензора деформаций (относительно группы преобразований, соответствующей типу симметрии среды [20]).

Для случая изотропной среды, упругие свойства которой описываются модулями объёмного сжатия K ( r ) и сдвига G ( r ) , мерами тензора повреждённости Q являются независимые материальные функции k и g , входящие в определяющие соотношения:

Оу ( r ) = [3 K ( r ) (1 - k) Djmn + 2 G ( r )(1 - g ) Hjmn ]- mn ( Г ) , где Djmn =(V3)5j5mn и Hijmn = Iijmn - Djmn. Введённые материальные функции выражают изменение деформационных свойств, определяющих поведение материалов при гидростатическом давлении и чистом сдвиге соответственно, и зависят от двух инвариантов тензора деформаций (или напряжений) j81) (r) = £kk (r) и j£2)(r)= -sij-sij , при записи которых использовано обозначение sj = е.-(1/3)-kk5ij.

При моделировании упругохрупкого поведения значения указанных функций скачкообразным образом изменяются от 0 до 1 при выполнении критериев разрушения:

g (je2')_

0    i ^{( 2) 2 )}

, J £ <  j £ Cr ,

1     i ^{( 2 )} > /^{( 2 )}

¹, j 8 — j 8 СГ ,

k (j.“.jE”)=

o, ( j - ²4 M j -^{2 1}

1, j? > j Г- ’ r A j "> 0.

> j ( ) A j ( ) J 8 cr - e

< 0 ) ,

В общем случае трансверсально-изотропной среды упругие характеристики определяются пятью техническим константами t , 1 , n , G ₁ и G I , а соответствующие им независимые функции к , ф , £ , р₁ и р // , связанные с тензором повреждённости Q [10], определяются четырьмя инвариантами тензора деформаций [20]: j £^{1 )} _£ ₁₁ + e ₂₂; j £^{2 )} = e ₃₃; j ^{( 3 )} _^(e_u -£ ₂₂ ) 2 + 4 e 2 ₂ ; j ^{( 4 )} = ^£ 2₃ + £ 2 ₃ . Для описания механического поведения структурных элементов воспользуемся определяющими соотношениями в следующем виде:

(Gn + G22 )/2 = t (1 — к)(£11 + £22 ) + 1 (1 — ф)£33 ,    (c11 - C22 )/2 = G1 (1 - р1 )(-11 - £22 ) ’

C33 = l (1 — ф)(£п + £22 ) + n (1 — ^)£33 ,

C12 = 2 G1 (1 — pi)£12, Пв = 2 GH (1 — р л ) £13 , G23 = 2 GII (1 -р II )£23 .

С целью учёта анизотропии структурных элементов при решении задач численного моделирования процессов деформирования и разрушения в условиях плоско-деформированного состояния (ось анизотропии лежит в плоскости деформирования) будем рассматривать три случая частичной потери несущей способности: от растяжения вдоль оси, перпендикулярной оси анизотропии ( j £1 ) = j £2 ); от растяжения вдоль оси анизотропии ( j £^{2 )} = j * 22 ) и от сдвига в рассматриваемой плоскости ( j £^{4 )} = j ( 42 ). Значения введённых функций повреждённости скачкообразно изменяются от 0 до 1 при выполнении критериев разрушения:

"’U 0 j 8 j - к j -Hi /">/■> I , j £ — j £ Cr ,	< * )^ Z1 *       /2 *^ /2 *       /4 *^ /4 * / . ( 1 )    . ( 2 ) • (3)\ J 0, j £    <  j £ cr   A j £    <  j £ cr   A j £    <  j £ Cr , ф( j £ , j £   , j £ )      1        .(1)      .(1)         .(2)      .(2)        .(4) .    .(4) 1. j >  J V j >  j V j >  j l_ , Je       £ c cr       Je       £ c cr       Je       £ c cr ,
.     Гл      i <2>     /2» r j ( 2 ) ;( 3 )A J 0, j £ <  j £ cr z ( J £ , J £ )      Il     ,-(2) > ,-(2) _ I f, j £    >  j £ Cr	A i (4Z4)                                        Гл ,    . Z2) A , 4:.   Z4) j £ <  j £ cr ,                / .(2)   .(3) \    J V,   j £ <  j £ cr A j £    <  j £ cr , V i (4)> i (4).           P 11 ( j 8 , j 8   )" 11.    j (2) > j (2)   V j (4) > j (4) . j £        j £ cr ,                                        I X, j £        j £ cr j £        j £ cr

Решая систему уравнений (1)–(3) с учётом граничных условий (4), получаем распределение неоднородных полей напряжений c j ( r ) и деформаций - j ( r ) в структурных элементах. С целью нахождения эффективных свойств структурно-неоднородной среды определим компоненты тензоров

**

макронапряжений с j и макродеформаций £ j (в дальнейшем все величины, относящиеся к макроскопическому уровню, будем помечать сверху звёздочкой). Компоненты тензоров макроскопических напряжений и деформаций вычисляются осреднением по объёму соответствующих тензоров на структурном уровне: с * = ¹ V J ^c ij ( r ) ^dV, ⁸*_у = ¹ V J ⁸ j ( r ) ^dV .

VV

Численное моделирование механического поведения зернистых структурно-неоднородных сред осуществлялось с использованием разработанного программного комплекса, в основу которого заложены метод конечных элементов, процедуры метода переменных параметров упругости и автоматического выбора шага нагружения [21], дающего возможность регистрировать разрушение минимально возможного числа конечных элементов на каждой итерации.

Численное решение поставленной краевой задачи сводилось к решению последовательности упругих задач при фиксированных значениях компонент тензора макродеформаций, которые соответствовали заданным граничным условиям. При этом с помощью процедуры автоматического выбора шага квазистатического нагружения вычислялись величины компонент тензора макродеформаций, при которых происходила частичная потеря несущей способности у минимально возможного числа элементов, участвующих в дискретизации области деформирования. Данная процедура способствовала сходимости и устойчивости численного метода расчёта и позволила отказаться от выбора фиксированного, наперёд заданного шага нагружения.

В программном комплексе на каждом шаге квазистатического нагружения реализовалась итерационная процедура поиска конечных элементов, в которых, вследствие перераспределения напряжений после предыдущих актов разрушения, не выполнялись критерии прочности. Итерационная процедура завершалась при выполнении критериев прочности во всех неразрушенных элементах дискретизации.

Для выбора на каждой итерации конечных элементов, подлежащих разрушению, вводился дополнительный параметр чувствительности, вследствие чего становилось возможным определение элементов дискретизации, находящихся очень близко к критическому состоянию в диапазоне ^0,995 ^ j ^Y 7 j 1 ^ 1. Такие элементы также считались разрушенными. Введение такого параметра позволило адекватно описать сценарий потери несущей способности зерна целиком в случае его нахождения в поле однородных деформаций. В то же время параметр чувствительности не оказывал никакого влияния на механизм трещинообразования, проявляющий себя в ситуации, когда при фиксированном шаге нагружения происходило разрушение некоторого числа конечных элементов. При этом степень дискретизации области деформирования в диапазоне от 30 до 80 конечных элементов, приходящихся в среднем на одно зерно, не оказывала заметного влияния на получаемые диаграммы деформирования и картины эволюции дефектных структур. В дальнейших расчётах степень дискретизации выбиралась таким образом, чтобы на каждое зерно приходилось в среднем около 50 конечных элементов.

Разработанный программный комплекс тестировался на различных модельных повреждённых средах, в частности, на задаче исследования напряжённого состояния в бесконечной пластине с отверстием внутри.

Рассмотрим плоскую модель зернистого композита, находящегося в условиях одноосного нагружения, в глобальной системе координат. Для этого на узлах правой границы области деформирования, имеющей квадратную форму, зададим перемещения и1 = и0 (здесь и в дальнейшем нижний индекс будет обозначать задаваемое направление), на левой — и1 = 0, на нижней и2 = 0, а верхнюю границу считаем свободной. Зернистый композит представим в виде среды, состоящей из ста зёрен, прочно соединённых по границам раздела. Упругие свойства у всех изотропных структурных элементов считаем одинаковыми: модуль упругости E = 10 ГПа и коэффициент Пуассона v = 0,25. Прочностные свойства зададим согласно двухпараметрическому закону распределения Вейбулла со средним значением прочностных свойств (782 Сr) = 1,25'10-3 и коэффициентом вариации kv = 0,5 в следующем виде: f(j) = c(j82)) bc exp -(jlb) , kv = ^Г‘(с)/[Г"(с)]2 -1, ^-2j = ьг((с+1)/с), где b и с — соответственно параметры масштаба и формы плотности распределения f (j(2)); Г'(с) = Г((c + 2)/c)

и Г "( с ) = Г ( ( c + 1)/ c ) — гамма-функции.

Дискретизация области деформирования проводилась в прикладном пакете программ ANSYS с использованием треугольных конечных элементов типа plane42. Конечноэлементная сетка строилась таким образом, что на каждое зерно приходилось в среднем по пятьдесят элементов.

Для количественного описания дефектной структуры зернистых структурно-неоднородных сред вводится величина повреждённости ю, которая определяется как объёмная доля зон разрушения, а при решении плоской задачи соответствует отношению площади конечных элементов, в которых произошло разрушение материала, к общей площади области деформирования. На рисунке 2 представлена расчётная диаграмма деформирования с*1 - е*1 и график повреждённости ю- 8,1. Из рисунка видно, что в начале процесса нагружения (до точки под номером 5) поля напряжений и деформаций однородны по всем зёрнам, что приводит к разрушению двух зёрен, имеющих минимальную прочность (Рис. 2, а). Как следствие, на диаграмме деформирования появляются вертикальные срывы между точками под номерами 1, 2 и 3, 4.

Появление первых разрушенных зёрен нарушает однородность полей напряжений и деформаций в области нагружения, что приводит к локализации процесса разрушения и образованию дефектов в виде трещин (Рис. 2, б , в , г ). Образованию, объединению или дальнейшему развитию трещин также соответствуют срывы на диаграмме деформирования (например, между точками под номерами 5 и 6 , 7 и 8 , 9 и 10 и так далее), обусловленные разрушением материала в пределах большого числа конечных элементов при фиксированном уровне макродеформации. Следует отметить, что потеря несущей способности только одного конечного элемента приводит к появлению вертикального срыва малой величины, который практически не заметен на кривой деформирования.

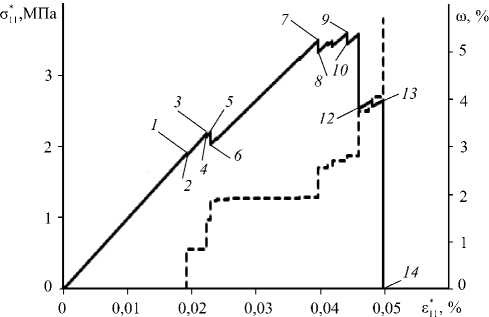
Рис. 2. Расчётная диаграмма деформирования (сплошная линия), график повреждённости (штриховая линия) и дефектные структуры ( а )–( г ) зернистого композита в некоторые моменты нагружения, обозначенные цифрами: структура в точке 5 ( а ); 9 ( б ); 13 ( в ); 14 ( г )

Анализ процессов микроструктурного разрушения показывает, что срывы на диаграммах деформирования связаны с явлением самоподдерживаемого разрушения, когда даже в случае «жёсткого» нагружения при определённой величине деформации происходит разрушение большого числа конечных элементов [22, 23]. В результате получены новые численные решения краевых задач, которые дают информацию о неоднородных полях напряжений и деформаций в отдельных структурных элементах, позволяют поэтапно описать эволюцию дефектной структуры в процессе нагружения, выделить эффективные деформационные и прочностные свойства и установить особенности механического поведения на закритической стадии деформирования зернистых композитов.

Ранее (см. [23]) авторами определены закономерности механического поведения зернистых структурнонеоднородных сред, связанные с формой и разбросом размеров элементов структуры при случайных значениях упругих и прочностных характеристик зёрен. При этом упругие свойства зёрен обладают изотропией и однородны в пределах каждого зерна. Модули упругости зёрен E_i изменяются по равномерному закону в интервале 0,8 E sr <  E i <  1,2 E sr , где E i = 10 ГПа. Коэффициент Пуассона для всех зёрен принимается равным 0,3. Прочностные характеристики зёрен удовлетворяют двухпараметрическому закону распределения Вейбулла: j j ( 2С r^ = 1,25-10 "³ , k_V = 0,5. Граничные условия задавались по аналогии с предыдущей задачей.

На основе установленных расчётных зависимостей показано, что при распределении значений модулей упругости по равномерному закону и прочностных характеристик по двухпараметрическому закону Вейбулла вытянутая форма зёрен предполагает существование большого числа концентраторов напряжений в области деформирования и тем самым приводит к снижению эффективных прочностных свойств (Рис. 3). Более значительный разброс относительных размеров структурных элементов вызывает в целом снижение деформационных и увеличение прочностных характеристик.

Проведены оценки влияния вида напряжённо-деформированного состояния на механическое поведение зернистых композитов (Рис. 4). Граничные условия задавались таким образом, что на левой и нижней границах области деформирования перемещения приравнивались к нулю ( и 1 = 0 и и 2 = 0 соответственно), а на правой и верхней и 1 = и ⁰ и и ₂ = и . При этом величины отношения и [и ⁰ выбирались равными -1; -0,5; 0; 0,5 и 1 с целью реализации разных видов деформированного состояния. Выявлены наиболее опасные схемы нагружения и благоприятные с точки зрения способности разрушенных в результате формоизменения элементов материала воспринимать нагрузку при отрицательных значениях первого инварианта тензора структурных напряжений. Наиболее опасными оказались кинематические условия нагружения, когда деформирование происходит по схемам Б ,1 = б 2 ₂ = б и б^ = -б 2 ₂ = б , при которых зернистая структурно-неоднородная среда обладает наименьшими значениями прочностных характеристик.

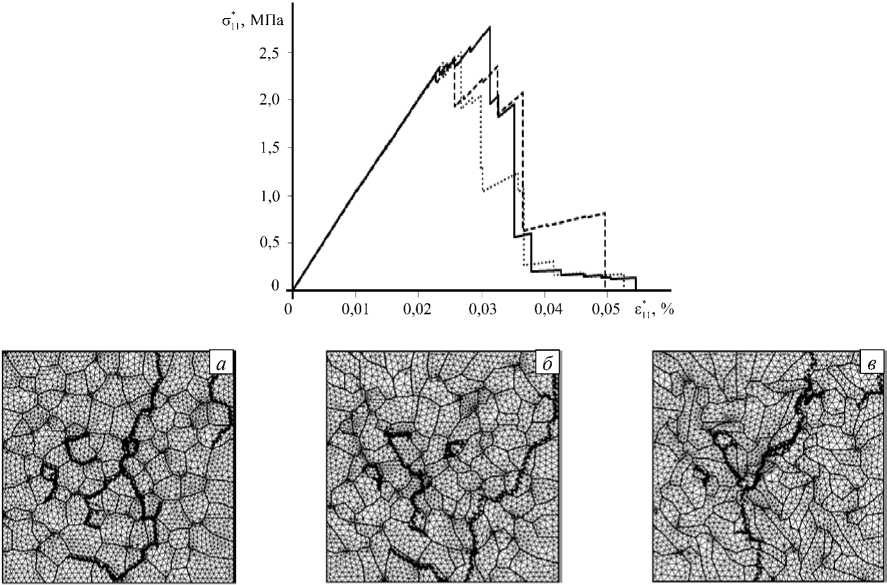
Рис. 3. Диаграммы деформирования и дефектные структуры зернистых композитов ( а )–( в ) с разными значениями коэффициента формы зерен k_f : 1 (сплошная линия) и ( а ); 2 (штриховая линия) и ( б ); 5 (пунктирная линия) и ( в )

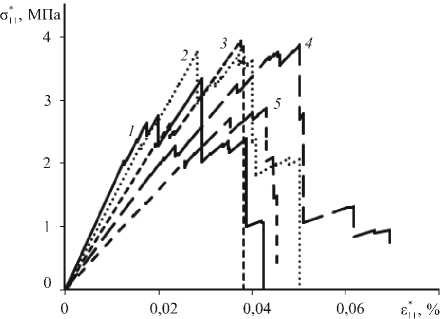
Рис. 4. Влияние вида напряжённого состояния на характер деформирования: б^ = б^ = б (линия 1 ); б^ = 2 б ^2 = б ( 2 ); б 11 = б , &* 22 = 0 ( 3 ); б^ = - 2 Б 22 = б ( 4 ); б^ = -б 22 = б ( Б> 0) ( 5 )

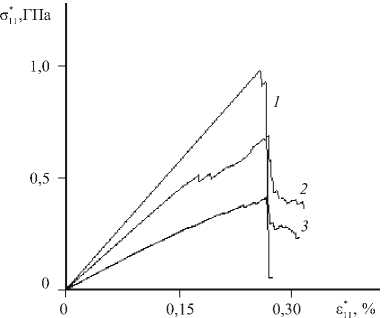
Рис. 5. Диаграммы деформирования зернистых композитов с разной ориентацией оси анизотропии в структурных элементах: в направлении деформирования (линия 1 ); по нормальному закону с параметрами математического ожидания 0° и среднеквадратического отклонения 20° ( 2 );

по равномерному закону в интервале от - 90 ° до 90 ° ( 3 )

Получены новые результаты численного моделирования процессов накопления повреждений для моделей зернистых структурно-неоднородных сред с учётом анизотропии свойств зёрен при различных законах статистического распределения параметра ориентации осей анизотропии структурных элементов в плоскости деформирования. Граничные условия задавались по аналогии с первой и второй задачами. На рисунке 5 показаны расчётные диаграммы деформирования для зернистых структур из 100 элементов, параметр ориентации которых удовлетворял равномерному и нормальному законам статистического распределения. Рассмотрен также случай, когда ориентация оси анизотропии у всех зёрен совпадала с направлением одноосного макродеформирования.

Анализ построенных диаграмм деформирования позволяет заключить, что зернистые композиты, имеющие структурные элементы, разориентированные по отношению к направлению макродеформирования, обладают меньшими значениями прочностных характеристик. При этом на диаграммах ярко выражена закритическая стадия их деформирования, что свидетельствует о лучшей способности этих материалов сопротивляться разрушению.

Таким образом, на основе вычислительных экспериментов получены данные о влиянии на механическое поведение зернистых композитов геометрических структурных параметров типа анизотропии, характеристик статистических законов распределения упругих и прочностных свойств структурных элементов, вида макрооднородного напряжённо-деформированного состояния.

С целью исследования возможностей описания механического поведения структурно-неоднородной среды на стадии деформационного разупрочнения в терминах эффективных характеристик в работе рассмотрена геометрическая модель зернистой структурно-неоднородной среды, состоящей из большого числа упруго-хрупких, идеально связанных между собой структурных элементов, геометрия которых совпадала с элементами дискретизации при использовании в численном решении задачи метода конечных элементов. Упругие свойства элементов структуры считались однородными по всему объёму (модуль Юнга Е = 10 ГПа, коэффициент Пуассона v = 0,25).

Рассчитаны четыре варианта структуры, прочностные свойства элементов которой были случайными и соответствовали двухпараметрическому закону распределения Вейбулла со средним значением предела прочности структурных элементов ^а⁰^ = 10 МПа и заданными коэффициентами вариации k_v = 0,3; 0,5; 0,7 и 0,9. Граничные условия задавались в перемещениях следующим образом: на правой границе области деформирования и 1 = и ⁰ , на левой — и 1 = 0, на нижней — и ₂ = 0, на верхней — и ₂ = 0.

В исследуемой области неоднородной среды выбиралось не менее десяти подобластей с возрастающим числом структурных элементов, для которых решались краевые задачи механики неупругого деформирования при макрооднородном деформированном состоянии и устанавливались зависимости макронапряжений от макродеформаций. Данные, оформленные в виде диаграмм деформирования с ниспадающим участком для подобластей с одинаковым количеством структурных элементов, осреднялись. Вычисления проводились для подобластей с числом структурных элементов N , равным 500, 1000, 2500, 5000, 10000 и 20000.

Данные вычислительных экспериментов показали, что, кроме размерной зависимости прочности, в значительно большей степени масштабный фактор проявляет себя на стадии деформационного разупрочнения. Соответствующие расчётные кривые приведены на рисунке 6 для коэффициентов вариации прочностных свойств k_v = 0,5 и 0,7. Аналогичные кривые получены в [24] для коэффициентов вариации 0,3 и 0,9. Из рисунка видно, что с увеличением числа элементов структуры и, соответственно, размеров расчётной области наблюдается вырождение ниспадающей ветви полной диаграммы деформирования. Представленные результаты дают основание для формулирования гипотезы существования масштабного эффекта на стадии разупрочнения материалов, заключающегося в зависимости параметров ниспадающей ветви диаграммы от количества структурных элементов в области деформирования.

(З'.МПа

Л2',МПа

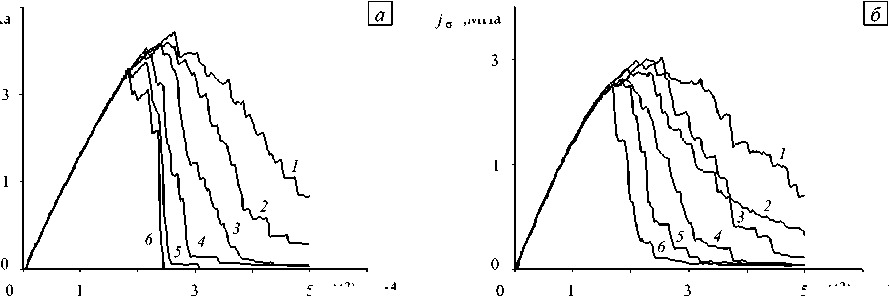
5 ю-

5 J'?'. IO"⁴

Рис. 6. Диаграммы деформирования в зависимости от количества структурных элементов N : 500 (линия 1 ); 1000 ( 2 ); 2500 ( 3 );

5000 ( 4 ); 10000 ( 5 ); 20000 ( 6) (коэффициенты вариации прочностных свойств k v = 0,5 ( а ); 0,7 ( б ))

Для количественного описания осреднённых диаграмм деформирования использовался энергетический подход, применяемый в механике разрушения . Согласно этому подходу работа внешних сил есть сумма энергии упругой деформации и работы разрушения. Следовательно, при полном разрушении исследуемой области, когда второй инвариант тензора напряжений имеет нулевое значение при заданной схеме нагружения, работа внешних сил равняется работе разрушения. Параметром описания масштабного эффекта в плоском случае служила удельная работа разрушения A_p V . Полной работе разрушения A_p соответствует площадь под диаграммой деформирования.

На рисунке 7 представлены вычисленные и аппроксимирующие зависимости удельной работы разрушения как функции размера области деформирования для четырёх вариантов прочностных свойств элементов структуры. Аппроксимация выполнена степенной функцией вида: A p V = C " N k , где C и k — коэффициенты аппроксимирующей функции. Их значения для разных генераций прочностных свойств приведены в таблице.

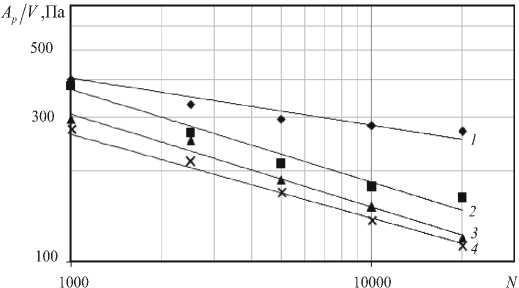
Рис. 7. Вычисленная (помечена символами) и аппроксимированная (линии 1 – 4 ) удельная работа разрушения в зависимости от размера области N для коэффициентов вариации прочностных свойств k_V : 0,3 ( ♦ и линия 1 ); 0,5 ( ■ и 2 ); 0,7 ( ▲ и 3 ); 0,9 ( X и 4 )

Таблица. Значения коэффициентов степенной аппроксимирующей функции

k V	C	k
0,3	1177,634	0,155
0,5	3095,709	0,307
0,7	2576,058	0,308
0,9	1784,734	0,277

Разработанные комплексы программ для численного моделирования процессов неупругого деформирования и структурного разрушения зернистых композитов рассматриваются как основа для получения новых данных о закономерностях их механического поведения, выработки рекомендаций по изменению структуры с целью улучшения эффективных деформационных и прочностных свойств материалов и планирования экспериментальных исследований [25] для проверки выявленных закономерностей механического поведения новых композиционных материалов.

Для подтверждения гипотезы существования масштабного эффекта на стадии разупрочнения материала, сформулированной на основе результатов численного моделирования, была разработана и реализована программа экспериментов на одноосное растяжение плоских стальных образцов с различным соотношением длины и ширины рабочей части. Эксперименты проводились на базе Центра экспериментальной механики Пермского национального исследовательского политехнического университета. Использовались электромеханическая испытательная система Instron 5882 с максимальной нагрузкой 100 кН и автоматический бесконтактный видеоэкстензометр AVE, обеспечивающий погрешность измерения 1 мкм при помощи специальным образом нанесённых на образец меток.

Проведённые и представленные в работе [26] экспериментальные исследования позволили установить существенную зависимость ниспадающего участка диаграммы от размера образцов. Обнаруженные закономерности на качественном уровне согласуются с зависимостями, полученными в результате математического моделирования процесса деформирования и структурного разрушения неоднородной среды, и свидетельствуют в пользу гипотезы существования масштабного эффекта на стадии разупрочнения материалов.

Работа выполнена в рамках Договора № 13.G25.31.0093 c OАO «Мотовилихинские заводы» на выполнение работ по теме «Создание высокотехнологичного машиностроительного производства на основе современных методов проектирования изделий и гибких производственных процессов прецизионной обработки металлов».