Моделирование связанных процессов, сопровождающих набор ранней прочности цементной полифракционной системой

Химические превращения в цементной системе при затворении водой проходят в условиях многофазности, многостадийности и влияния таких факторов, как водоцементное отношение, концентрации исходных компонентов, активность цемента и его фазовый состав, вид заполнителя, время и температура твердения, пористость и других. При затворении водой цементная система включает три фазы: твердую, жидкую и газообразную. В процессе гидратации (химических превращений при наборе прочности) жидкая и газообразная составляющие формируют поровое пространство, которое непрерывно заполняется гелеобразными продуктами их реакции. Выявление механизмов гидратации цемента, обусловленных особенностями образования структуры с учетом тепло- и массопереноса, важно для развития методов управления процессами создания цементного камня с заданными свойствами.

Прогнозирование структурных изменений цементного камня с применением компьютерного моделирования является актуальным направлением, дающим возможность отслеживать изменения внутренней структуры при варьировании большого числа факторов. При этом анализ эволюции характеристик представительного объема цементного камня позволяет оценивать развитие структуры бетона во всем получаемом объеме [1 –3] , а моделирование физических процессов, сопровождающих химические реакции в процессе гидратации, — исследовать факторы, влияющие на скорость и глубину превращений и отражающие развитие системы в целом.

К настоящему времени разработано множество математических представлений гидратационных процессов в системе «цемент–вода», однако каждая модель имеет ряд ограничений и допущений. Первые простейшие модели описывали изменения отдельных сферических частиц цемента при их контакте с водой. В качестве репрезентативной единицы отслеживалась гидратация C 3 S, которая характеризовала развитие всей системы [4, 5] . Некоторые модели уделяли внимание процессу диффузии — процессу переноса воды через слоистые мембраны растущего продукта гидратации [6] . Более развитые модели отображали общую гранулометрическую картину цементных систем и учитывали влажность, водоцементное отношение и удельную поверхность частиц различного размера [7, 8] . Известен ряд тезисов о случайном зародышеобразовании при столкновении гидратирующих

Статья опубликована в открытом доступе по лицензии CC BY 4.0

частиц, вызванном увеличением их объема, что описано уравнением Аврами [9] . Однако модели данного кластера [10, 11] изображают процессы гидратации на плоской статичной поверхности. В конце 90-х годов прошлого века настало время нового поколения моделей, способных в кубическом объеме смеси представлять частицы цемента в виде сфер и учитывать множество факторов, хотя первые из них значительно ограничивались в функциональности нехваткой вычислительных мощностей [12] . Так были созданы модели HYMOSTRUC [13] , CEMHYD3D [14] и HydratiCA [15] с учетом химии фаз, образования пор, подвижности частиц в растворе, при этом каждому исходному материалу предписывается спектр свойств и правил взаимодействия.

В ходе эволюции вычислительных технологий появились новые возможности и способы прогнозирования структурных изменений при гидратационных процессах цементных систем, основанные на опыте ранних разработок. В совокупности известные методики моделирования и симуляции представляют собой эффективные средства исследования, однако действующие граничные условия и принимаемые допущения ограничивают универсальность их применения. Данное направление исследований непрерывно развивается и нуждается в качественно новых подходах, основанных на фундаментальных законах природы, способных расширить сферу приложений моделей и усовершенствовать различные аспекты прогнозирования химических превращений.

• 2.    Моделирование процесса гидратации

Развиваемая модель гидратации цементной многокомпонентной системы включает в себя ряд элементов физико-химических процессов, отражающих начальное структурообразование композита. За основу исследования взят подход к моделированию связанных процессов в реагирующих средах, предложенный в [16] . Модель представляется совокупностью уравнений, описывающих нестационарный тепловой баланс и макрокинетику химических превращений. Термомеханическое состояние и фазовый состав реагирующей среды рассматриваются одновременно на макро- и микроскопических уровнях.

Исследуемый материал полагается смесью реагентов — цемента и воды, и инертного наполнителя (различных фракций песка и продукта реакции). Особенности режимов подготовки смеси и первичного уплотнения ее компонентов, обладающих различной плотностью и размером элементов, обуславливают образование макроскопической структуры исходной смеси. Таким образом, исходная макроскопическая структура цементного бетона — это неоднородная и полифракционная система, образуемая порами и агломератами частиц. Для решения задачи исследования особенностей формирования структуры бетона берется модельный объект в виде слоя, состоящего из представительных объемов (реакционных ячеек), имеющих одинаковое характерное направление изменения концентрации компонентов и пор. Модельный слой среды в виде реакционных ячеек — упакованных элементов макроскопической структуры, показан на рисунке 1а (позаимствован из [16] ).

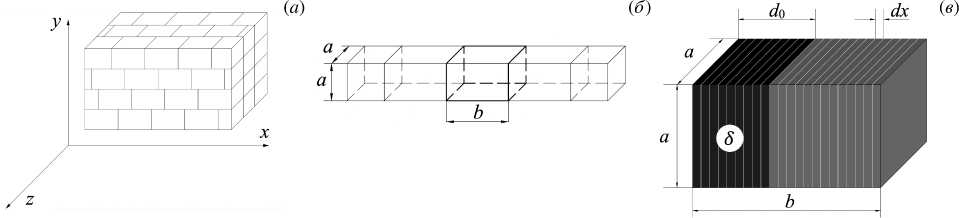
Рис. 1. Модельный слой среды ( а ), характерная последовательность реакционных ячеек ( б ), отдельная реакционная ячейка ( в ) [16]

Постановка задачи об экзотермических химических превращениях в гетерогенной системе может содержать неоднородность распространения фронта температур. В такой формулировке задача рассмотрена Алдушиным А.П. и Хайкиным Б.И. [17]. Показано, что вследствие более медленного, по сравнению с процессами теплопереноса, протекания диффузионных процессов химического превращения дисперсных компонентов температурное поле гетерогенной экзотермически реагирующей системы можно считать макроскопически одномерным в направлении, перпендикулярном боковой поверхности слоя (вдоль оси x). Это позволяет для модельной последовательности реакционных ячеек по толщине слоя ввести следующие положения: 1) частицы реагирующих компонентов (цемента) представляются как множество точечных источников тепла, а теплоперенос определяется эффективными значениями теплофизических характеристик гетерогенной системы; 2) закономерности процесса гидратации цементной многокомпонентной системы описываются уравнениями сопряженных задач макрокинетики химических превращений и тепло- и массопереноса вдоль последовательности реакционных ячеек.

Характеристикой степени макроскопической неоднородности модельного слоя служит параметр b/a, где b — длина ячейки (Рис. 1б ). В рамках модифицируемой модели принимается, что концентрационная неоднородность по объему ячейки задается вдоль b — в направлении изменения концентрации компонентов смеси и относительного объема пор, так как предполагается, что заданная доля жидкой фазы δ сконцентрирована у левой грани ячейки в зоне d 0 , протяженность которой обуславливается размером агломератов частиц.

Таким образом, ячейка структуры является представительным объемом реагирующей среды с условием тепловой гомогенности в сечениях a x а, отражающим эффективные свойства всего материала [16] . На каждом временном этапе моделирования все текущие концентрации компонентов и пор корректируются с учетом изменения как размеров микрослоев ячеек, так и концентраций, и плотностей компонентов.

• 2.1.    Учет формирования субструктуры контактирующих частиц на разных иерархических уровнях

При моделировании структуры дисперсного тела необходимо учитывать формирование в какой-либо крупной фракции полидисперсного (по размеру) наполнителя — песка, субструктур контактирующих частиц. Эти субструктуры способны существенно влиять на получаемую структуру и ее физико-механические характеристики [18] . Субструктуры в модельном теле при достижении плотной упаковки частиц инертного наполнителя могут образовываться на разных структурных уровнях и для различных фракций. Под отдельной фракцией понимается набор частиц, диаметр которых характеризуется определенным значением с погрешностью до 5%. Допускается, что в пределах фракции частицы наполнителя имеют одинаковую форму, и оптимизацию состава смеси можно проводить по размерам отдельных фракций.

В модельном теле присутствуют частицы наполнителя трех фракций. Для размеров частиц отдельных фракций в вычислительных экспериментах используется отношение:

d i- 1 <  0 . 25 d i , (1)

где i — номер отдельной фракции. При этом мелкие частицы располагаются между крупными. Размеры частиц соотносятся как d max > d midi > d min . После формирования в какой-либо из фракций субструктуры контактирующих частиц уменьшить пористость в теле будет невозможно без механического воздействия. Учитывается, что предельная объемная концентрация частиц каждой фракции не превышает максимальную концентрацию, достижимую при насыпной плотности частиц этой фракции наполнителя. Каждая фракция частиц характеризуется собственным значением предельной объемной концентрации, величина которой устанавливается экспериментально и зависит от формы частиц соответствующей фракции.

Если формирование субструктуры обуславливается взаимодействием в локальных объемах рассматриваемой ячейки периодичности крупных частиц d max , то можно считать, что этот размер определяет состояние всего объема ячейки. В свою очередь в пределах каждого локального объема гетерогенного модельного тела эта субструктура считается локально макроскопической, поскольку по ней оценивается остаточная пористость всего модельного тела. Если концентрация частиц наполнителя достаточна для формирования субструктуры, то в момент достижения модельным телом состояния с максимально плотной упаковкой частиц уменьшить его пористость без механического воздействия будет невозможно. Исходная объемная концентрация доли D max частиц максимального размера представляется как D max C R , где C R — объемная концентрация твердой фазы . Образование субструктуры на макроуровне происходит тогда, когда концентрация доли частиц максимального размера D max C r / (1- C P ) , где CP — начальная концентрация пор, становится равной предельному значению объемной концентрации частиц C bd max рассматриваемой фракции. Выражение для оценки минимального относительного объема пор, при котором возможны уплотнение модельного тела на макроуровне и рост концентрации D max до максимальной величины, имеет вид [18] :

• C P 1 = ¹ - D max C R /C bd max .

С уменьшением пористости модельного тела на величину C P 1 крупные частицы наполнителя объединяются в силовую субструктуру. При ее образовании дальнейшее локальное снижение пористости ограничивается. Величина локальной минимальной пористости оценивается как

Pminl = Ср -Ср 1, при этом CP > CP1.

На каждом временном шаге вычислений в процессе итерационного уточнения текущей структуры и свойств осуществляется пересчет всех объемных концентраций компонентов относительно исходного состояния. При выполнении локального условия C P < C P 1 крупными частицами d max субструктуры не формируются. В таком случае в модельном теле возможно возникновение субструктур из частиц наполнителя средних размеров d midi . Получаемая субструктура отвечает мезоскопическому уровню. Аналогичный процесс наблюдается на микроуровне (создаются субструктуры из частиц d min ) при условии C P < C P 2 и C P > C P 3 .

Обобщение вышеизложенного позволяет представить такую последовательность действий для учета формирования субструктуры частиц инертного наполнителя:

• –    задать минимальную пористость модельного тела;

• –    если для некоторого микрообъема модельной среды C P 1 < C P , то минимальную пористость оценить согласно выражению (2) ;

• –    если C _{P 2} < C _P , то для проверки величины прогнозируемой минимальной пористости перейти к соотношению:

P min2 = (C p - C p 2 )(1- ф o D max C R );                              (3)

– если C P 3 < C P , то для определения прогнозируемой минимальной пористости применить формулу:

^P min3 = ^(C P ^— C P 3 )⁽1 ^— ф 0 ^{( D} max + D midi ) CR. );

• –    если условия формирования субструктуры частиц наполнителя на макро-, мезо- или миниуровне не выполняются, то задать P _min = P _min0 (в качестве малого значения «нулевой» исходной пористости P _min0 в вычислительных экспериментах используется величина 0.01);

• –    если условие ограничения на размер частиц отдельных фракций (1) соблюдается, то три фракции частиц d _max , d _midi , d _min объединить в одну с эффективным значением размера частиц:

  d ef =

  
  

d max D max + d midi D midi + d min D min

D max + D midi + D min

.

Проделаны вычислительные эксперименты по оценке минимальной пористости получаемого модельного тела в зависимости от фракционного состава инертного наполнителя. В таблице, взятой из работы [18] , приведены возможные распределения исходных частиц инертного наполнителя по размерам, удовлетворяющие условиям полидисперсности (1) . Из таблицы видно, что наименьшим значением минимальной пористости, определяемой для составов 1–3, соответственно, соотношениями (2) – (4) , обладает модельное тело 1-го состава.

Таблица. Распределение по размерам частиц инертного наполнителя модельных составов

Состав	Размеры фракций, мкм				Объемные доли фракций
	d max	d midi	d min	d nano	D max	D midi	D min	D nano
1	16.00	4.00	1.00	0.01	0.88	0.03	0.02	0.07
2					0.03	0.88	0.02	0.07
3					0.02	0.03	0.88	0.07

Таким образом, структура модельного тела в значительной степени зависит от того, в какой из фракций наполнителя формируются субструктуры частиц. При использовании наполнителя из преимущественно крупных и средних фракций, удовлетворяющих ограничению на размер частиц отдельных фракций смеси (1) , обеспечивается наибольшая возможность получения низкопористой структуры модельного тела.

• 2.2.    Макрокинетика химических превращений

Моделирование процесса химических превращений всех активных фаз бетона в представительном объеме возможно с позиций макрокинетических подходов, поскольку химические превращения протекают в реальных условиях многофазности и многостадийности реакций, когда особое внимание необходимо уделять процессам диффузии, теплопередачи и конвекции.

Кинетика процесса гидратации цемента удовлетворяет уравнению Аррениуса, устанавливающему зависимость константы скорости реакции k от температуры T (его эффективность для описания химических превращений цементных систем доказана в [19] ):

k = Aexp(-Ea/RT), где R — универсальная газовая постоянная (8.3144 Дж/моль·К), Ea — энергия активации, A — предэкспоненциальный множитель, который является фактором частоты столкновения частиц с подходящей пространственной ориентацией.

Согласно физическому смыслу, предэкспоненциальный множитель равен константе скорости реакции при температуре, стремящейся к бесконечности. Однако не каждое столкновение частиц приводит к химической реакции. Молекулы должны обладать необходимым запасом энергии (энергией активации), чтобы при столкновении инициировалось химическое взаимодействие между ними.

Скорость химических превращений можно оценить по скорости теплового потока dQ/dt в процессе калориметрических испытаний:

dQ A     - E a

= Qm ' ■        'Ф где ф (z) — функция торможения, зависящая от степени превращений, Qm — максимальное количество выделенного за сутки тепла.

Для определения кажущейся энергии активации E a использовались значения скорости тепловыделения, полученные методом изотермической калориметрии при испытаниях цементного камня при различной температуре.

• 2.3.    Фильтрационные процессы

В рамках модели, модифицированной для учета особенностей ранней гидратации цементной системы, рассматриваемый материал представляется в виде пористого твердофазного каркаса, насыщенного жидкостью. Движение жидкой фазы по массиву при наличии свободной пористости происходит как фильтрационный процесс вследствие действия капиллярных сил. В общем случае скорость фильтрации обуславливается количеством жидкости, прошедшим через единичную площадку поперечного сечения среды [20] . Фундаментальное соотношение теории фильтрации связывает скорость жидкости — u ( x ) , градиент давления — ^ P l , и массовую силу — g . Для фильтрации в изотропной среде данное уравнение принимает следующий вид:

υ

^ P i + p i g = F ^{( |u| )} p.

Здесь pl — плотность жидкости [21] ; функция F (| u |) описывает зависимость силы сопротивления при движении жидкости в пористой среде от скорости фильтрации. В случае ламинарного течения в неподвижной пористой среде жидкой фазы с вязкостью µ можно использовать закон Дарси:

F (u) = (n/K )и, где K — коэффициент проницаемости пористой среды, η — коэффициент динамической вязкости жидкости.

В данной работе связь между скоростью фильтрации воды и градиентом давления в насыщенной пористой изотропной среде рассматривается при пренебрежимо малых значениях вязких напряжений в жидкости, инерционных сил, пульсационного переноса импульса и кинетической энергии пульсационного движения [22] . В силу этих допущений применимость закона Дарси для реагирующего микрослоя материала обуславливается ламинарным течением жидкости в нем. Скорость фильтрации жидкости в модельной пористой среде, состоящей из однородных твердых сферических частиц диаметром d , находится по формуле [16] :

-∇ P l Πd ²

U = 180(1-П 2)M, где Π — пористость, M — динамическая вязкость жидкой фазы, которая зависит от температуры.

Капиллярные поры являются частью поровой системы цементного камня и образуются с накоплением избыточной воды, не связанной химически с цементом. В обычных условиях насыщения, то есть при отсутствии внешнего воздействия, вода, заполняющая поры, удерживается в материале силами капиллярного давления. Важно учитывать, что объем капиллярных пор сокращается по мере увеличения степени гидратации за счет наполнения гидратными новообразованиями [23] .

Фильтрация жидкости в рассматриваемой среде обусловливается разностью плотностей исходных веществ и формируемых продуктов реакции, воздействием термокапиллярных сил, возникающих вследствие разности коэффициентов температурного расширения компонентов, и капиллярным давлением. Капиллярное давление — значимая сила на границе раздела фаз, связанная с транспортными процессами в формируемом цементном камне. Для расчета капиллярных сил применяется формула [24]:

P = nad c cos в.

При этом а — поверхностное натяжение жидкости (для воды при T = 20 ^О С принимается равным 72.86 ^ 10 - ³ Н/м); d_c — диаметр капилляра, [м]; cos в — угол смачивания или краевой угол на границе «жидкость-стенка капилляра» (для минеральных материалов cos в =1 [25] ).

Из закона Пуазейля следует, что средний диаметр пор находится по формуле:

dc = 4^2K/П, в которой коэффициент проницаемости K не зависит от свойств жидкости, а обуславливается только свойствами пористой среды (в основном геометрией порового пространства). Для пористой среды, состоящей из сферических твердых частиц диаметром d, коэффициент принимается таким [22]:

П 2 d ²

K = ---------..

180(1 - П ) ²

С учетом этого выражения капиллярное давление определяется по формуле:

\dnacosв IП 3(1 - п ) V 10'

• 2.4.    Тепловой баланс

В исследуемой среде процессы установления теплового баланса описываются одномерным уравнением теплопереноса с переменными коэффициентами:

∂T ∂ psCs dt = dx

∂T

λ s ∂x

+q v+ + q v - ,

где q _{v +} и q _{v -} — источники и стоки, отображающие экзо- и эндотермические эффекты физико-химического поведения реагирующей смеси. Так, стоки тепла позволяют учитывать теплопотери, и все теплофизические параметры в уравнении считаются зависящими от структурных характеристик и температуры. Все коэффициенты уравнения теплопереноса полагаются эффективными локальными характеристиками гетерогенной среды.

Использование эффективных параметров тела для описания процесса теплопереноса в пористых средах является объемно-усредненным моделированием, которое имеет ряд преимуществ по сравнению с прямым точечным моделированием. В работе [26] доказано, что второй подход, устанавливающий граничные условия на разделе фаз при записи уравнений сплошной среды, трудоемок для вычислений и точность решения существенно не повышает. Метод осреднения, который подробно представлен в [22] , заключается в выделении элементарного объема гетерогенной смеси, включающего границу раздела фаз (межфазную поверхность). Этот объем много меньше объема тела и значительно больше объемов микронеоднородностей (пор). В данной работе тепловые процессы в рассматриваемой среде предлагается описывать двухтемпературными уравнениями теплового баланса [26] для температур каркаса и жидкости.

При наличии порового давления вследствие действия термокапиллярных сил осуществляется фильтрация жидкости. Температуры каркаса и жидкой фазы могут различаться, и тогда температурный режим реагирующего тела определяется температурными профилями твердофазного каркаса ( T _s ) и жидкой фазы ( T _l ). В этом случае уравнения теплового баланса представляются в виде:

∂T s

^{(1 — n} i) P s c s—^~ + ^a v ^f T ^(T s ^{— T} l)=~^~ ^ s ^{(1 — n} i ) л;— +q v+ +q

∂t                ∂x          ∂x

∂x

v - ,

∂Tl                  ∂ niPlcl      av fT (Ts — Tl ) = ^~

∂t                ∂x

∂T l λ l Π l

∂x

∂T l c l G l , ∂x

где ρ s — эффективная плотность материала каркаса, ρ l — плотность жидкой фазы, c s — эффективная теплоемкость материала твердофазного каркаса, c _l — теплоемкость жидкой фазы, Π _l — эффективная пористость каркаса, α _v — коэффициент объемного внутреннего теплообмена между жидкой фазой и каркасом, λ _s — эффективный коэффициент теплопроводности каркаса смеси, λ l — коэффициент теплопроводности жидкой фазы, G l = p lu — расход жидкой фазы, f_T — относительная поверхность теплообмена в сечении слоя (отнесена к полной поверхности порошковых частиц смеси до уплотнения), υ — скорость движения жидкой фазы.

Начальные условия задачи теплового баланса формулируются так:

t = t* : Ti = Ts(x), где Ts (x) — исходное распределение температуры по толщине реагирующего слоя на момент времени t*.

Граничные условия имеют вид:

∂Ts      ∂Tl x = 0: Ts = T = T ; x = nb: ——=0, —— = 0.

∂x      ∂x

Задание на внешней поверхности x = 0 температуры T = T , отличной от начальной внутренней температуры слоя, позволяет производить анализ влияния внешней температуры на процессы гидратации цементных систем.

Для моделирования процесса установления теплового баланса при эндотермическом фазовом переходе допускается, что действие стоков энергии q v - инициируется при достижении температуры пороговых значений фазовых превращений и компенсирует действие источников тепла механической и химической природы q v + до полного завершения фазовых переходов — до исчерпания затрат энергии на фазовые переходы в каждом микрообъеме реагирующего материала.

Процессы установления теплового баланса моделируются с позиции теплофизики зернистой среды с эффективными свойствами. В теплофизическом отношении зернистый слой представляет собой систему с многообразными механизмами переноса тепла: теплопроводность и термические напряжения внутри зерна; конвективный теплообмен между зерном и потоком жидкости; каркасная теплопроводность зернистого массива; теплопроводность неподвижной жидкой фазы в слое; теплообмен слоя с внешними границами; перенос тепла излучением [27] . При наличии открытой пористости и градиента порового давления — необходимых условий фильтрации, в насыщенном зернистом слое реализуются условия конвективного теплообмена, характеризующего потоковый массоперенос жидкой фазы.

Коэффициент объемного внутреннего теплообмена α _v , входящий в уравнения, может быть оценен по среднему значению коэффициента теплоотдачи зерна α _z , который в рамках решения модельной задачи для сферической частицы, омываемой потоком жидкости, равняется [27] :

az = 0.25^pcccvPr-2/3, где ^ = 1.09^1-(1- П)2/3^, Pr — число Прандтля, v — скорость фильтрации.

Сложность моделирования гетерогенных сред заключается в описании эффективного коэффициента теплопроводности, учитывающего вклады различных составляющих. Так, коэффициенты теплопроводности могут находиться из решения модельных краевых задач теплопроводности:

Х (12-11 П ) + 11 П -6 У [ Х (12-11 П ) + 11 П -6] 2 + (7 хП +24-7 П )( х +17-10 П )

= z   7хП+24-7П   +                 7хП+24-7П                ’ где х = Ac/Az, Az — эффективный коэффициент теплопроводности зерна.

Таким образом, краевая задача теплового баланса реагирующего слоя представляется в виде двухтемпературной нестационарной нелинейной краевой задачи теплопроводности для каркаса и жидкой фазы смеси. Для ее численного решения применяется неявная разностная схема, обладающая большей, по сравнению с явными схемами, устойчивостью при наличии фазовых переходов [28] .

При определении расхода жидкой фазы в уравнении теплового баланса используется уравнение Дарси (см. предыдущий подраздел 2.2). Градиент давления при этом заменяется приближенным конечно-разностным соотношением:

vp=pm-pm _1)/h, где h — шаг конечно-разностной сетки.

Все коэффициенты, участвующие в расчетах, в каждый момент времени зависят от локальных значений температуры, пористости и концентраций соответствующих химических превращений, фазовых переходов и фильтрации. Все параметры модели для каждого микрослоя уточняются итерационно на каждом шаге по времени.

• 2.5.    Блок-схема компьютерного моделирования

• 3.    Экспериментальная часть и результаты

  • 3.1.    Исходные данные для вычислительного эксперимента

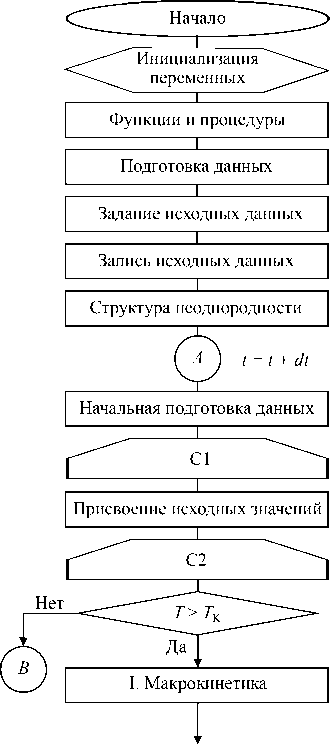
Алгоритм решения связанной задачи оценки прочности цементной полифракционной системы на ранних стадиях гидратации включает исследование макрокинетических процессов, фильтрации жидкой фазы и теплового баланса, составляющих основу разработанной компьютерной модели. Блок-схема алгоритма представлена на рисунке 2.

Исходные данные для компонентов реагирующей смеси, учитывающихся при моделировании процесса гидратации, выбраны на основе анализа литературных источников [29 –35] . Энергия активации и предэкспоненциальный множитель (макрокинетические параметры) получены по результатам лабораторного эксперимента.

Блок процедур и функций

Задание исходных данных, изменяемых в процессе вычислительного эксперимента

Задание исходных данных, неизменяемых в процессе вычислительного эксперимента

Возможность формирования субструктуры контактирующих частиц инертного наполнителя на различных иерархических уровнях.

Оценка минимальной пористости

Вычисление возможных теплопотерь на фазовые переходы и запоминание значений суммируемых массивов перед итерациями

Начало цикла итерационного уточнения

Задание значений массивам, суммируемым в процессе итераций

Цикл по микрослоям

Проверка достижения температурой значения T K – температуры инициирования реакции

Решение задач макрокинетики

Рис. 2. Блок-схема алгоритма решения связанной задачи оценки прочности цементной полифракционной системы

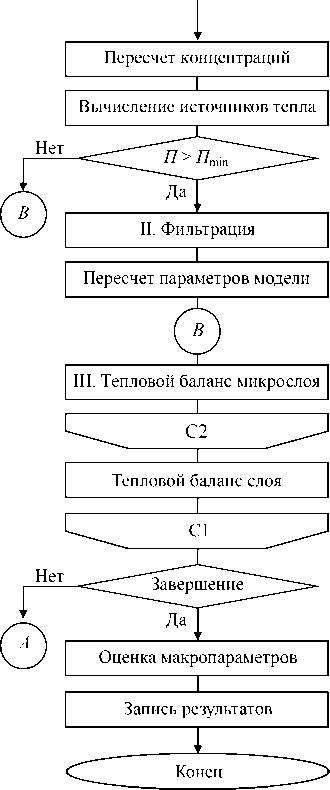
Рис. 2. Продолжение

Пересчет концентраций компонентов смеси после химических превращений на шаге по времени

Вычисление источников в уравнении теплопроводности с учетом стоков

Проверка наличия открытой пористости и градиента температур

Решение задачи фильтрации жидкой фазы на шаге по времени

Учет изменения пористости и концентраций компонентов в процессе фильтрации жидкости за интервал по времени dt в двух смежных микрослоях

Построение уравнений теплового баланса микрослоя с эффективными теплофизическими параметрами, источниками и стоками

Конец цикла по микрослоям

Решение краевой задачи теплового баланса и определение полей температуры по толщине реагирующего слоя в момент времени t

Конец цикла по итерациям

Проверка условий завершения превращений в реагирующем слое

Вычисление макроскопических параметров механохимических процессов

• 3.2.    Определение энергии активации

Кажущаяся энергия активации может быть установлена путем механических или калориметрических измерений. Первый способ позволяет производить расчет по данным испытаний, однако он трудоемок в вычислительном плане и сопровождается погрешностями, что снижает точность полученных результатов. Калориметрический подход осуществляется в изотермических или адиабатических условиях. Суть изотермического испытания состоит в фиксации температурного параметра, от которого и зависит кажущаяся энергия активации.

В рамках данной работы произведен калориметрический анализ системы в соответствии с ГОСТ 310.588 «Цементы. Метод определения тепловыделения». Данный метод дает возможность изучить кинетику реакции гидратации цемента исходя из термодинамики твердения раствора. Калориметрия является методом оперативного прогнозирования прочностных характеристик цементных систем с доказанной корреляцией между тепловыделением и набором прочности [29 –35] . Тепловыделение с учетом экзотермического характера гидратации цемента позволяет оценить стадию завершенности процесса и установить связь между степенью гидратации и возрастом цементного камня. Так, информацию о количестве выделившегося тепла можно использовать для косвенного сравнения прочностных характеристик составов с одинаковым минералогическим содержанием [36] . В настоящем исследовании проводился анализ динамики тепловыделения цемента при 20, 30 и 40 ^о С.

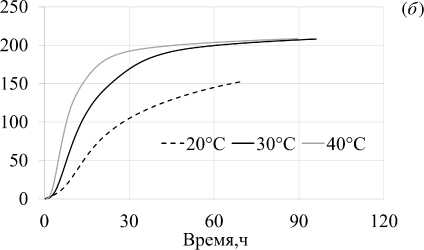
В качестве исследуемого материала применялся цемент (C) марки М500, которой соответствует класс прочности I 42.5, произведенный ООО «Петербургцемент». Инертным материалом служил строительный песок. Эксперименты проводились с помощью 8-канального изотермического калориметра TAM Air фирмы TA Instruments, разработанного для измерений тепловых эффектов в минеральных связующих материалах с высокой стабильностью и точностью. Все калориметрические каналы сдвоенного типа, то есть состоят из камеры образца и камеры эталона. Прибор специально оптимизирован для создания и изучения новых композиций для цементного и железобетонного производства. Испытания заключались в следующем: в ампулы объемом 20 мл засыпалось точно отмеренное на весах количество цемента, а именно 6 г, и затворялось 3 мл воды (W ), то есть обеспечивалось отношение W/C = 0.5. Емкость герметизировалась крышкой и помещалась в камеру для образца. Эталонную камеру калориметра занимала ампула с инертным заполнителем (песком). Внутри каждого канала обеспечивалась постоянная температура 20,30 или 40оС. Длительность каждого эксперимента составляла 5 суток. В течение всего испытания отслеживались суммарная тепловая энергия и тепловой поток содержимого ампул. По итогам калориметрического анализа получались их нормализованные значения с учетом массы образцов (Рис. 3).

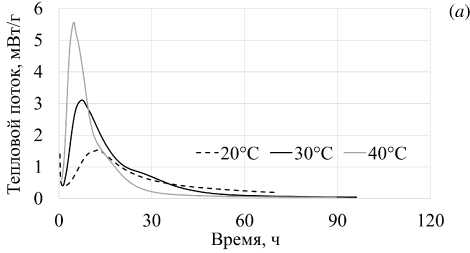
Рис. 3. Распределения теплового потока ( а ) и суммарной тепловой энергии ( б ) образцов цемента

Степень гидратации определялась по изменению теплоты гидратации [19] :

dz_ 1 dQ dt Qm dt где t — текущее время, Qm — максимальное значение суммарной тепловой энергии, [Дж]. Если ввести k = dz/dt и при этом принять

Ink = lnA - Ea/(RT), то параметры макрокинетики найдутся из решения методом наименьших квадратов задачи оптимизации

F (A,Ea) ч min при условии, что A = const. В качестве целевой принималась функция F вида:

n

F = X(xi - yi )2, i=1

где x i — среднее значение логарифма константы скорости реакции гидратации (определ яем ое методом изотермической калориметрии при температуре T i по результатам экспериментов числом i = 1 ,n); y i = In k. В соответствии с вычислениями, принимались значения: энергия активации E a = 90 кДж, предэкспоненциальный множитель A = 6 • 10 6 .

• 3.3.    Характеристики цемента в соответствии с фазовым составом

• 3.4.    Вычислительный эксперимент

Цемент — гидравлическое вяжущее вещество, получаемое при измельчении минерального сырья и являющееся основным компонентом бетонных и других строительных смесей, которые используются при ремонтных и реставрационных работах. Типичный цемент можно охарактеризовать следующим минералогическим составом: 67% СаО, 22% SiO 2 , l5% AI 2 O 3 , 3% Fe 2 O 3 и 3% других компонентов. В данной работе в состав цемента входят следующие, так называемые клинкерные минералы, процентное соотношение которых, согласно [37] , следующее: C 3 S — 57%, C 2 S — 25%, C 3 A — 8%, C 4 AF — 10%. Известно, что молярная масса C 3 S есть 228.3 г/моль,

C ₂ S — 172.22 г/моль, C 3 A — 270.18 г/моль, C ₄ AF — 485.94 г/моль. Молярная масса цемента соотносится с долями каждого клинкерного компонента согласно смесевой модели. Обычно клинкер содержит четыре главные фазы, называемые как алит (Ca 3 SiO 5 или C 3 S), белит (Ca 2 SiO 4 илиC 2 S), алюминатная (Са 3 Аl 2 O 6 или C 3 A) и ферритная (4CaO·Al ₂ O 3 ·Fe ₂ O 3 ·SiO ₂ или C ₄ AF). В небольших количествах присутствует и несколько других фаз, таких как щелочные сульфаты и оксид кальция. Качество реакции гидратации цемента определяется, в первую очередь, вяжущими свойствами его состава. В большинстве моделей [4, 5] кинетика твердения цементного камня основывается на реакции C 3 S, так как минерал вносит больший вклад в набор прочности и своей интенсивностью характеризует общий механизм гидратации смеси. Однако даже на ранних стадиях схватывания необходимо учитывать вклад всех минералов в соответствии с их массовыми долями, скоростью и интенсивностью реакции.

Реакция гидратации цемента является экзотермическим процессом. Так, при гидратации рассматриваемых клинкерных минералов выделяется следующее количество тепловой энергии: C 3 S — 502 Дж/г, C 2 S — 260 Дж/г, C 3 A — 867 Дж/г, C 4 AF — 419 Дж/г [37, 38] .

Клинкерные минералы реагируют с разной скоростью и интенсивностью. Гидратация C 3 A предопределяет процесс схватывания цемента путем формирования алюминатной структуры. Далее образуются силикатные структурные компоненты, вызванные реакцией C 3 S и C ₂ S. Согласно работе Г. Ямагучи [39] , в первые сутки наблюдается следующая степень гидратации клинкерных минералов: C 3 S — 40–70%, C 2 S — 7–15%, C 3 A — 40–60%, C ₄ AF — 20–40%, или после усреднения 55% C 3 S, 11% C ₂ S, 55% C 3 A и 30% C ₄ AF. По результатам расчета на основе смесевой модели теплота реакции гидратации для принятых концентраций клинкерных минералов составляет 522.43 Дж/г.

В качестве объекта исследования была выбрана цементная система при отношении 1:3 цемента к полидисперсному наполнителю (песку). Изучались физико-химические механизмы взаимодействия компонентов смеси в процессе гидратации. Мелкий заполнитель и продукт реакции считались инертными материалами.

Моделирование позволяет анализировать степень гидратации по массовой доле прореагировавшего вещества — µ, в определенные моменты времени исходя из степени образования гидратированного цементного камня из смеси цемента и воды. Для оценки влияния параметров, обуславливающих характер структуры цементного камня, на процесс его гидратации рассмотрена зависимость прироста массовой доли прореагировавшего вещества от водоцементного отношения (Рис. 4) , минимальной пористости (Рис. 5а ) и характеристики концентрационной неоднородности b/a (Рис. 5б ).

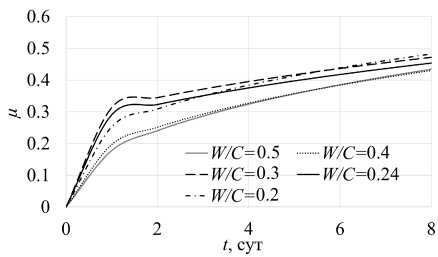
Рис. 4. Прирост массовой доли прореагировавшего вещества при различных водоцементных отношениях ( а ) и в зависимости от отношения W/C при t = 2 сут ( б )

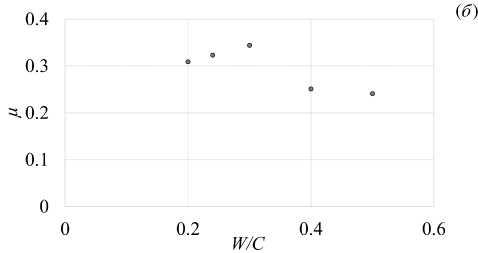
Полученные данные коррелируют с доказанными зависимостями влияния водоцементного отношения на скорость гидратации системы [40, 41] . Известно, что смесь цемента и песка способна удерживать такое количество воды, которое будет связано на поверхности частиц твердой фазы, в порах и капиллярах. При недостатке жидкой фазы увеличивается число пор вследствие жесткости неуплотненной смеси, что ведет к ослаблению сцепления между частицами. При избытке воды имеет место расслаивание смеси и растрескивание затвердевшего камня. Однако в пределах допустимых значений при одинаковых всех внешних факторах наблюдается общая тенденция к снижению прочности бетона при повышении величины отношения W/C [41] . Стоит отметить, что при W/C< 0 . 28 может происходить явление «саморазрушения особо плотного цементного камня» [42] , что

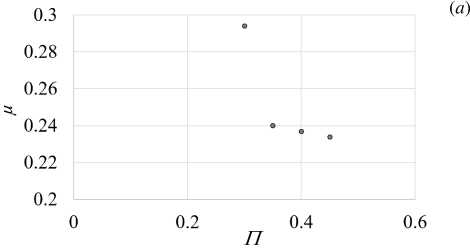
Рис. 5. Зависимости массовой доли прореагировавшего вещества от пористости при b/a = 2.5 и W/C = 0.5 ( а ) иот степени макроскопической неоднородности b/a ( б )

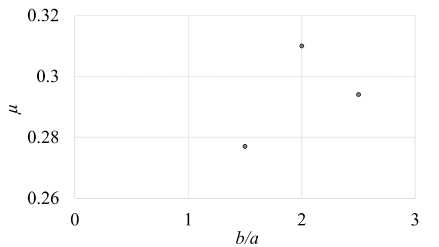
( б )

способствует снижению прочности. Отношение W/C может считаться оптимальным с позиции формирования продуктов гидратации такой плотности, которая не ведет к возникновению внутренних напряжений в цементном камне. Соответствующие этому состоянию системы значения водоцементного отношения находятся в пределах 0.3–0.4 [42] , с чем совпадают результаты, полученные при моделировании в настоящей работе.

Представленные на рисунке 5а графики отвечают основным закономерностям, наблюдаемым при определении прочности цементного камня. С ростом пористости упаковка частиц в едином монолите становится менее плотной, что обусловливает снижение прочности, которая в свою очередь характеризуется степенью гидратации [43] . Таким образом, модифицированная модель позволяет оценить влияние основных структурных характеристик на степень и глубину химических превращений, сопровождающих реакцию гидратации цемента.

Значимое влияние на процесс гидратации цементной системы оказывает температура реакции. С ее повышением преумножается проникающая способность молекул воды в создаваемых в результате адсорбционного понижения прочности условиях для разрушения цементных зерен, то есть увеличения концентрации растворенного вещества на границе двух фаз [44] . В данной работе рассмотрено влияние повышенных температур на степень превращения. Моделирование проводилось при температуре 20, 30 и 40 ^о С (Рис. 6) .

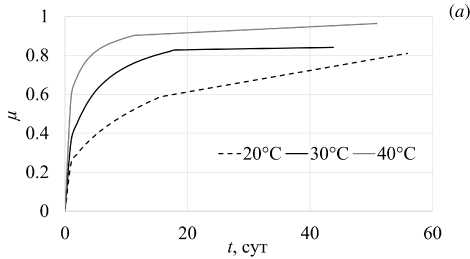
Рис. 6. Массовая доля продуктов гидратации при различной постоянной температуре как функция времени ( а ); зависимость массовой доли прореагировавшего вещества от температуры ( б )

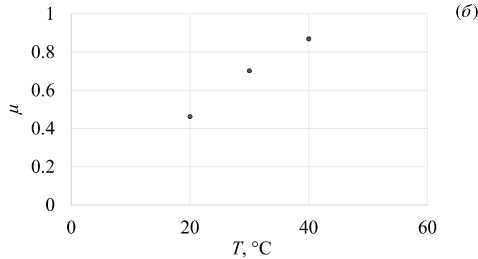
По итогам моделирования заключено, что повышение начальной температуры реакции способствует более интенсивному образованию продуктов гидратации вследствие активизации взаимодействия цемента и воды. Характер представленных графиков прироста массовой доли прореагировавшего вещества при различных температурах (Рис. 6а ) соответствует виду кривых, отражающих тепловыделение системы при гидратации, полученных при изотермической калориметрии (Рис. 3б ). Данный факт подтверждает адекватность используемой модели, описывающей гидратационные процессы в цементных системах.

• 4.    Заключение

Разработанная модифицированная модель полифракционной цементной системы позволяет исследовать процессы гидратации на ранней стадии набора прочности в зависимости от параметров структуры и состава исходной смеси. Предложен подход для нахождения оптимальных соотношений между размерами частиц полифракционного заполнителя и их объемными долями в модельном теле для обеспечения максимально плотной упаковки.

По итогам проведенных вычислительных экспериментов можно заключить, что предложенная модель корректно представляет влияние водоцементного отношения, пористости и начальной температуры на степень превращения системы, так как полученные результаты коррелируют с известными закономерностями, наблюдаемыми на практике при определении прочности цементного камня или бетона. Продемонстрировано следующее: увеличение начальной пористости способствует снижению степени гидратации в цементном камне, чем объясняется формированием менее плотной упаковки частиц; повышение водоцементного отношения приводит к снижению выхода продукта реакции из-за наличия химически несвязанной воды (это качественно подтверждает известные закономерности); рост начальной температуры реакции обеспечивает более интенсивное протекание реакции гидратации. Таким образом, доказывается адекватность разработанной модели, которая может корректно описывать на начальных этапах механизмы и закономерности структурообразования цементного камня в процессе гидратации с наличием полифракционного заполнителя. Возможно дальнейшее развитие данной модели применительно к гидратационным процессам в многокомпонентных системах с учетом влияния дополнительных компонентов.

Исследование выполнено при финансовой поддержке Программы стратегического академического лидерства «Приоритет 2030» БФУ им. И. Канта.