Моделирование свободных колебаний звукопроводящей системы реконструированного среднего уха

Механические повреждения мембраны, а также ограниченная подвижность цепи косточек среднего уха, вызванная отосклерозом и другими заболеваниями, может приводить к значительному снижению порога акустической восприимчивости или к полной потере слуха. В ряде случаев, с целью устранения патологических изменений или механических повреждений, в оториноларингологии прибегают к частичной или полной реконструкции среднего уха [1]. Объем реконструкции зависит от степени повреждения каждого составляющего элемента колебательной системы среднего уха. Классификации используемых на практике реконструктивных операций приведены в [1-3].

В настоящей работе рассматривается случай частичной реконструкции [1, 4], когда барабанная перепонка замещается искусственной мембраной, изготовленной из хряща [5], а вместо поврежденной цепи косточек «молоточек-наковальня» вводится Т-образный протез (рис. 1).

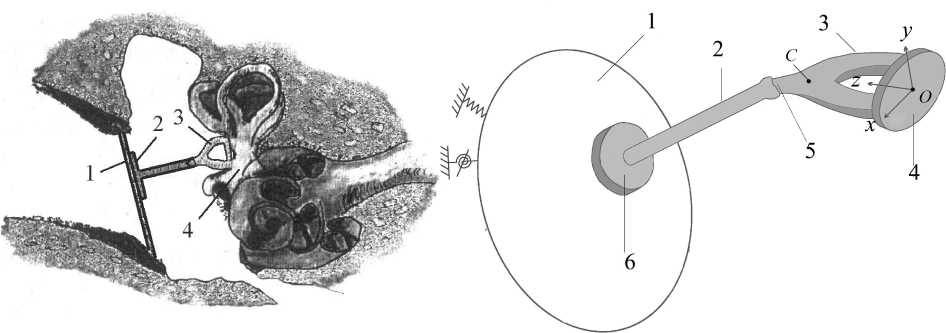
Рис. 1. Реконструированное среднее ухо: 1 – Рис. 2. Геометрическая модель реконструированного восстановленная мембрана, 2 – Т-образный   среднего уха: 1 – восстановленная мембрана, 2 – Т- протез, 3 – стремя, 4 – основание стремени    образный протез, 3 – стремя, 4 – основание стремени, 5 – головка стремени, 6 – основание протеза

Последний вставляется таким образом, что его конец соединяется с головкой стременной косточки [6], а шляпка склеивается с мембраной. Будем рассматривать протез как недеформируемый стержень. Тогда, считая, что склеивание протеза с мембраной является жестким, будем моделировать последнюю как тонкую кольцевую пластинку (рис. 2), изготовленную из вязкоупругого изотропного материала.

Основание стремени представляет собой овальную жесткую пластинку, которая крепится при помощи связок к костной ткани. Жесткостные свойства связок овального окна были изучены в работе [7]. Введем прямоугольную ортогональную систему координат Oxyz с центром в основании покоящегося стремени (рис. 2). Стременная косточка обладает шестью степенями свободы. Пусть U^T=(U_x, U y , U z , a x , a y , a z ) -вектор перемещений и поворотов стремени в системе координат Oxyz , где U x , U y , U z – проекции перемещения центра масс С на оси Ox, Oy, Oz , а a _x, a y , a z - повороты стремени вокруг этих осей, соответственно. Обозначим через F – вектор усилий и моментов, действующих со стороны связок овального окна. Тогда

F T = C RB U T, здесь

	" 51,40 - 0,24 - 1,37   0,04мм 9,66мм 0,35мм "
	49,20 - 0,60 - 7,87 мм - 1,01мм - 8,40 мм
	27,80   0,37 мм   17,10 мм   0,96 мм
C RB = c ref	8,29 мм2 0,58 мм2   2,60 мм2	(2)
	29,70мм2   1,60 мм2
	_ sym                                        12,90 мм2 _

– матрица жесткости, характеризующая упругие свойства связок овального окна [7], где коэффициент c ref колеблется в пределах 0,035 до 0,050 Н/мм.

М. I

Рис. 3. Механическая модель реконструированного среднего уха: 1 - восстановленная мембрана, 2 - Т-образный протез, 3 - стремя, 4 - основание стремени

Механическая модель

Существует несколько способов установки Т-образного протеза, зависящих как от степени патологии, так и от индивидуальной архитектуры полости среднего уха. Поскольку амплитуда колебаний пластинки (искусственной мембраны) является наибольшей в центре, то оптимальным с точки зрения передачи энергии является такое положение протеза, при котором его основание находится как можно ближе к центру пластинки. Здесь рассмотрим упрощенную модель, когда центры пластинки и основания протеза находятся в одной точке O p (рис. 3).

Анализ матрицы (2) показывает, что сопротивление связок овального окна будет наименьшим, если стремя совершает поступательные перемещения в направлении оси Oz и повороты вокруг оси Ox (рис. 2). Поэтому для анализа малых (линейных) низкочастотных колебаний можно рассмотреть плоские движения цепи “протез-стремя”. На рис. 3 показана упрощенная модель реконструированной колебательной системы при плоском движении протеза и стремени. Ее положение однозначно определяется величинами W, 0 p , 0 s , y c , z c , где W - нормальный прогиб пластинки, 0 p и 0 s ⁼ a x - углы поворотов протеза и пластинки вокруг осей O p x и Ox соответственно, а y c , z c - координаты центра масс стремени в исходной системе координат Oxyz (здесь Z c * 0).

Уравнения движения

Уравнение свободных колебаний кольцевой вязкоупругой, изотропной пластинки, моделирующей искусственную мембрану, имеет вид [8, 9]:

D А ² Е [ W ( r , ф , t )] + g ^S W ⁽ r , ^ф , t ) = 0.                            (3)

d t ²

Здесь

t

E [ z ( r , ф , t )] = z ( r , ф , t ) - J R ( t - t ) z ( r , ф , т ) d т

-∞

• -    интегральный оператор с ядром релаксации R(t) , А - оператор Лапласа в полярной системе координат r , ф ( b < r < a ) с центром в точке O p , D = Eh ³/[12(1- v 2 )] -цилиндрическая жесткость пластинки, h - толщина пластинки, E , v - мгновенные модуль Юнга и коэффициент Пуассона, с - поверхностная плотность материала.

По внешнему контуру барабанная перепонка граничит с волокнисто-хрящевым кольцом (мембранным кольцом) [10], упругие свойства которого непостоянны по периметру [11] и могут сильно колебаться у каждого человека. Учитывая данное обстоятельство, рассмотрим два варианта крепления пластинки по внешнему контуру (r = a) - жесткую и упругую заделку. Для жесткой заделки х d W (r, ф, t) А

W ( r , ф , t ) =---------- = 0 при r = a

dr и для случая упругой заделки

, _ ~ , d W ksiW = QL, kst — = Ml при r = a, о r где

Q l = D E

5 ( 52W 1 5W 1 52W) dr     + r   + 7 .)

M l =eJ D

5 ² W    ( 1 5 W 1 5 ² W )

2 + c+       25r2     V r dr r2 дф ,

• -    перерезывающая сила и изгибающий момент в пластине, k si , k_st - коэффициенты, определяющие жесткость мембранного кольца на нормальное перемещение и поворот пластинки, соответственно. Значения k si , k_st для нижней и верхней частей мембранного кольца, найденные экспериментально для среднего уха в норме, приведены в работе [11]. При возрастании параметров k sl , k st жесткость мембранного кольца увеличивается, а в пределе, при k si , k_st ^ да , условия упругой заделки (5) переходят в условия жесткого крепления пластинки.

Радиально симметричные колебания пластинки, соответствующие поступательному движению протеза, были изучены в работах [9, 12, 13]. Здесь рассмотрим случай, когда пластинка имеет один узловой диаметр. Тогда граничные условия на внутреннем контуре примут вид

W = b cos ф sin 0 p ( t )

d W n       к

---= 0 при r = b.

d r

Заметим, что для собственных форм колебаний пластинки с n >  2 числом узловых диаметров протез является неподвижным. Поэтому данные формы колебаний не представляют интереса и здесь не рассматриваются.

Вращательное движение протеза описывается уравнением

Ip 0 p = Mop, где Ip - момент инерции протеза относительно оси Opx, MOp - главный момент всех сил, действующих на протез относительно оси Opx. Момент состоит из двух компонент

M op = M Op ) + Mo p , -

Здесь

M o Р ⁾ =

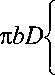
д ² - (W ) д r²

f 1 5- ( W ) - ( W ) 1 ,а_А__ы..

+ ol----1 + b— A—(W)

V r д r      r ² )   д r

- равнодействующая изгибающих моментов и моментов перерезывающих сил (6) в пластине относительно оси O p x, действующих по внутреннему контуру ( r = b ), а

М ОР = l p Y k ( t )cos О р ( t ) + l p Z k ( t )sin 0 p ( t )                      (11)

• - момент силы F _k = ( Y_k, Z_k ) в шарнирном соединении К , действующий со стороны протеза, где l_p - длина протеза, Y k , Z k - проекции силы F _k на оси Oy , Oz , соответственно. Стремя совершает сложное плоское движение, состоящее из поступательных движений вдоль осей Oy, Oz и вращения вокруг оси Сх (здесь Сх - ось, проходящая через центр масс С параллельно Ох ).

Поступательные движения описываются двумя скалярными уравнениями ms У c = Yk - c 22 ( lp sin 0 p - ls sin 0 s),                         (12)

m s z c = Z k - c зз ( l — l p cos 0 p - l_s cos 0 s ),                       (13)

где (0, y_c, z_c ) - координаты центра масс С , l_s - длина стремени (расстояние от его головки до основания), l = l_s + l_c , с ii - диагональные элементы матрицы (2), взятые с коэффициентом c_re f .

Уравнение вращения стремени вокруг оси Сх имеет вид

Is0s = Yklc cos 0s - Zklc sin 0s - c440s ,(14)

где I s - момент инерции стремени относительно оси Cz , l c - расстояние от головки стремени К до центра масс. Параметры I s и l_c найдены экспериментально в [7].

Координаты центра масс С стремени однозначно определяются углами 0p, 0s: y, = l„ sin 0n - L sin 0,, zr = l -1„ cos 0 „ - L cos 0S.(15)

c p pc sc    p    pcs

Малые колебания

Уравнения (8), (12) - (15) являются нелинейными относительно 0 _p ( t ) , 0 _s ( t ) , Y k ( t ) , Z_k ( t ). Рассмотрим малые колебания системы. После линеаризации приходим к системе линейных уравнений:

fа2нт  Г1 ант а 1

Ip0p = -пbDj^-W + d -Y-Wl —W 1 +b^A-W)^  + lpYk ,(16)

ar ²        y r д r        ²     )    д d r J A

^ О/                               «7r ms(lp0p -lc0s) = Y -c22(lp0p -ls0s), Zk = 0,(17)

Jc0s = Yklc - c440s .(18)

Проведем разделение переменных

W (r, ф, t) = w (r )cos ф e - in t,(19)

(0 p, 0 s, Yk, Zk ) = e ~in t (0 p, 0 s, yk, zk ),(20)

где Q = го +i а , го - частота колебаний, a - декремент колебаний. Подставив (19) в (3), (5), (7), приходим к дифференциальному уравнению

" d ²     1 d

--у +--

_V dr ² r dr

—

1 w — k⁴w = 0

относительно w с граничными условиями f 1         22

k_slw ( a ) — A ( Q ) l w ( a ) + — w ( a ) —2" w ( a ) + ~ w ( a ) I = 0,

V a aa kst w'(a) — A(Q)| w'(a) + — w(a) — —y w(a) | = 0,

V a a2

w ( b ) = b 0 p , w ' ( b ) = 0 ,

где

, 4    —Q ²

k =------,

A ( Q )

( да

A

а A ( Q ) = D 1 — J R ( t ) e ^{— i Q} t dt .

V о

Задача (21), (22) имеет решение в виде w (r) = bM ■ [m 31 J1 (kr) + M 3! Y (kr) + M 3311 (kr) + M 34 K1 (kr)]

где М - матрица размерности 4 x 4 с элементами:

W  ( 2 D

M11  I 3

Va

—

W ( 2 D M12 =1 ~

Va

W f 2 D M13 =1 ~

Va

W ( 2 D M14 =1 ~

Va

\

D

2 D _т,

k_sl J 1 ( ka ) + DJ Г( ka ) +— J f( ka ) —     J ‘ ( ka ) ,

J                    a          -

A

D

-

k_sl Y 1 (ka ) + DY ; (ka ) + — } ; ' ( ka)

—

—

-

7

a

a

2D Y '( ka ) , a

т/

D

",

2 D ₇,

k_sl I 1 ( ka ) + DIK ka) +— I ‘ ( ka ) — I ‘ ( ka ) ,

7                    a          ~2

A

a

D

2 D

k_sl K 1 ( ka ) + DK( ka ) + — K ( ka ) — K ( ka ) ,

7

a

a

D—

A

D—

M 21 = DJ f( ka ) +I-- k_s t J ( ka) — —J i ( ka) ,

a

( D—

7

A

a

D—

M 22 = DY(ka ) +-- k_s t Y(ka) --г Y ; (ka ) ,

V a

7

a

M 23 = DI 1 (ka ) + f D ^—— k s, I ; ( ka ) —     1 1 ( ka) ,

Va                 2

D—

D—

7

A

a

D—

M 24 = DK ( ka ) + 1—— k st K ‘ ( ka ) — -— K 1 ( ka ) ,

a

7

a

M ₃₁ = J 1 ( kb) , M ₃₂ = Y ( kb ) , M ₃₃ = 1 1 ( kb ), M ₃₄ = K 1 ( kb ),

M 41 = J ‘ ( kb ) , M 42 = Y l ’ C kb ) , M 43 = I ‘ ( kb ) , M 44 = K ‘ ( kb) ,

J 1 ( x ), Y 1 ( x ) – функции Бесселя первого и второго рода первого порядка, I 1 ( x ), K 1 ( x ) – модифицированные функции Бесселя первого и второго рода первого порядка, а

M з j ( j = 1,—,4) - соответствующие миноры матрицы М .

Подставляя (20) в уравнения (16) – (18) и учитывая (23), приходим к соотношениям zk = 0, 0. =

l p l c ( m s Q 2 - c 22 )

m s ^Q l c ^{- c} 44 + J c ^{Q - c} 22 l s l c

⁰ p , У к =

l p ( m_s Q ² - c -)( C 44 - J c Q ²) ₀ m s ^{Q l}c ^{- c} 44 + J c ^{Q - c} 22 ^ls^lc

и трансцендентному уравнению

^T^ P [ b ^ ¹ M 31 J 1 ( ^kr ) + ^M 32 Y ( kr ) + M 33 ¹ 1 ( kr ) + ^M 34 ^K 1 ( kr ) ) , = b

+

+ 2 -_T ( M 31 J i ( kr ) + M 3₂ 1 ; ( kr ) + M 33 1 1 ( kr ) + M 34 K / kr ) )   + — ( M 31 J /kr ) +

оr                                                       = ^b b

2 - —

+M Y(kr)+M i(kr)+M K(kr))  +   . (M J(kb) + r = b

+ M 32 Y 1 ( kb ) + M 33 1 1 ( kb ) + M 34 K 1 ( kb ) )) -

1 ² ( m Q ² - c , J( c₄₄ - J Q ² ) p s          22    44 c

- J Q ² = 0. ^p

m Q212 - c44+ J Q2 - cjl s c 44 c          22 s c относительно комплексной частоты колебаний Q.

Численный анализ

В среде Maple V.5 были выполнены расчеты первых шести собственных частот системы, соответствующих радиально несимметричным формам колебаний, при различных значениях входящих в задачу геометрических и физических параметров. В таблицах 1-3 приведены значения собственных частот системы, рассчитанные для случая несимметричных колебаний без учета вязкости реконструированной мембраны ( R - 0).

Поскольку механические свойства хряща, используемого для реконструкции мембраны, сильно колеблются (например, для суставного хряща модуль упругости меняется от 2.3 до 50 МПа [14]), было исследовано влияние мгновенного модуля упругости на собственные частоты колебательной системы. В таблице 1 приведены значения частот системы в зависимости от модуля Юнга пластинки в случае жесткого крепления последней на внешнем контуре. Расчеты были выполнены при a =5 - 10^-3 м, b =2 - 10^-3 м, m s =3,5 - 10 -6 кг, m p =9 - 10 -6 кг, h =1,5 - 10 -4 м, — =1,2 - 10³ кг/м³, c_re f =0,035, l p =1,5 - 10 -3 м, l_s =1,5 - 10 -3 м, l_c =8,1 - 10 -4 м, I_c =4,97 - 10^-12 м, v =0,4. Как видно, жесткость восстановленной мембраны сильно влияет на спектр частот колебательной системы среднего уха.

Таблица 2 показывает, что при увеличении жесткости мембранного кольца значения собственных частоты увеличиваются, причем при k sl ^ да все частоты ю i стремятся к значениям, найденным для случая жесткого крепления на внешнем контуре.

Таблица 1

Зависимость собственной частоты ω _i (Гц) от модуля Юнга восстановленной мембраны в случае жесткого крепления на внешнем контуре

Е , 107 Н/м2	ω 1	ω 2	ω 3	ω 4	ω 5	ω 6
1,2	146	399	780	1288	1923	2684
3,2	240	670	1334	2227	3335	4650
5,2	303	780	1625	2682	4003	5589

Таблица 2

Зависимость собственных частот ω _i (Гц) от коэффициента k_sl в случае упругой заделки на внешнем контуре

k sl	ω 1	ω 2	ω 3	ω 4	ω 5	ω 6
103	80	280	793	1513	2469	3627
104	101	322	804	1522	2476	3630
105	201	424	849	1550	2490	3645
1010	240	670	1334	2227	3335	4650

Таблица 3

Зависимость собственных частот ω _i (Гц) от основания протеза b в случае упругой заделки на внешнем контуре

b , 10-3м	ω 1	ω 2	ω 3	ω 4	ω 5	ω 6
1	136	371	723	1190	1773	2473
1.5	176	485	953	1584	2310	3224
2	240	670	1334	2227	3335	4650

В таблице 3 приведены значения собственных частот в зависимости от радиуса основания протеза b в случае жесткого крепления на внешнем контуре при значениях a = 5 - 10 " ³ м, m s = 3,5 - 10 " ⁶ кг, m p = 9 - 10 " ⁶ кг, h = 1,5 - 10 " ⁴ м, с = 1,2 - 10³ кг/м³, C ref = 0,035, l p = 1,5 - 10 " ³ м, l s = 1,5 - 10 " ³ м, l c = 8,1 - 10 " ⁴ м, E = 3,2 - 10⁷ Н - м " ², I_c = 4,97 - 10 " ¹² м, v = 0,4. Анализ таблицы 3 указывает на сильную зависимость собственных частот от радиуса основания протеза, замещающего цепь «молоточек-наковальня».

В таблицах 4-5 приведены значения собственных частот и декрементов колебаний системы, найденные с учетом вязкости искусственной барабанной перепонки для случая жесткого крепления реконструированной мембраны на внешнем контуре. Следует отметить, что вопрос об определении вязкоупругих характеристик биологических тканей и, в частности, суставных хрящей, из которых изготавливается реконструируемая мембрана, является достаточно сложной проблемой. Попытка определить адекватные физические соотношения для биологических тканей ( в том числе и для тимпанической мембраны) с учетом ярко выраженных эффектов релаксации напряжений приводят к довольно сложным нелинейным моделям [15], реализация которых сильно затрудняет расчеты. Отметим также, что физические свойства трансплантируемой ткани с течением времени сильно меняются. Учитывая данные обстоятельства, были проведены расчеты для двух простейших вязкоупругих моделей, характеризующихся, соответственно, экспоненциальным ядром

R ( t ) = Ae ^-в t , (27)

Таблица 4

Значения собственных частот ω _i (Гц) и декремента колебаний в случае экспоненциального ядра скорости релаксации

Номер частоты	1	2	3	4	5	6	7	8
ω	176,470	240,678	396,522	670,740	825,186	1334,24	1485,12	2226,73
α	0,01124	0,21026	0,01421	0,21032	0,01947	0,21035	0,02058	0,21033

Таблица 5

Значения собственных частот ω i (Гц) и декремента колебаний в случае ядра Ржаницына

Номер частоты	1	2	3	4	5	6	7	8
Без учета вязкости	176,470	240,707	396,522	670,894	825,186	1334,64	1485,12	2227,32
ω	163,471	211,077	365,903	596,858	743,400	1197,68	1338,33	2010,94
α	2,43608	5,08983	5,13724	12,6037	13,8150	23,1714	24,8381	36,4745

Жесткое крепление

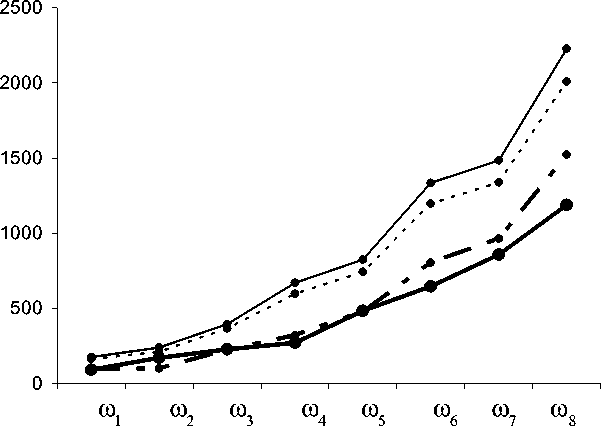
С учетом вязкости, в случае ядра Ржаницына

- Упругая заделка

Ухо в норме

Рис. 4. Собственные частоты колебательной системы среднего уха в норме, а также после хирургической реконструкции а также ядром Ржаницына

R ( t ) = A t ^{- s}e ^{-β t} .                                       (28)

В таблице 4 отображены значения собственных частот ω и декремента колебаний α для экспоненциального ядра при значениях A = 0,0422, β = 1,3, a = 5 ⋅ 10^-3 м, b = 2 ⋅ 10^-3 м, m s = 3,5 ⋅ 10^-6 кг, m p = 9 ⋅ 10^-6 кг, h = 1,5 ⋅ 10^-4 м, σ = 1,2 ⋅ 10³ кг/м³, c ref = 0,035, l p = 1,5 ⋅ 10^-3 м, l s = 1,5 ⋅ 10^-3 м, l c = 8,1 ⋅ 10^-4 м, E = 3,2 ⋅ 10⁷ Н ⋅ м^-2, I c = 4,97 ⋅ 10^-12 м, ν = 0,4. Нечетный номер частоты и декремента соответствуют радиально-симметричным колебаниям [9], а четный - радиально-несимметричным колебаниям, найденным из уравнения (26).

Аналогичные расчеты, выполненные в случае ядра Ржаницына с параметрами A = 0,4/Г(0.1), β = 1, s = 0,9, где Г(x) - гамма-функция, представлены в таблице 5. Значения остальных параметров колебательной системы взяты такими же, как и в предыдущем примере. Для сравнения приведены результаты расчетов в случае, когда вязкость материала во внимание не принимается (A =0). Видно, что учет вязкоупругих свойств мембраны приводит к снижению спектра частот. Как известно, вязкоупругая модель с ядром релаксации, имеющем особенность, наиболее адекватно описывает колебательные процессы в начальный момент времени [16]. Сравнение расчетов, приведенных в таблицах 4 и 5, показывает, что модель Ржаницына в большей степени учитывает эффекты релаксации напряжений, приводящих к затуханию колебаний реконструируемой системы среднего уха.

На рис. 4 для сравнения приведены результаты расчетов для уха в норме, выполненных методом конечных элементов [17] для упругой модели, а также в случае реконструкции при различных способах крепления искусственной мембраны с учетом и без учета вязких свойств последней. Анализ кривых указывает на то, что во всех случаях хирургическая реконструкция приводит к увеличению собственных частот колебательной системы среднего уха, не оказывая при этом заметного влияния на наинизший спектр частот.