Моделирование течения воздуха в упруго-деформируемой пористой среде, аппроксимирующей легкие человека: структура модели, ее основные уравнения и разрешающие соотношения

К настоящему времени многочисленными исследованиями доказано негативное влияние загрязнения атмосферного воздуха химическими веществами в различном агрегатном состоянии на здоровье человека, в том числе на его дыхательную систему [1 –3] . Существующие лабораторные и инструментальные методы позволяют выполнить комплексное обследование пациента, получить объективную картину текущего состояния его здоровья, корректно поставить диагноз и наметить схему лечения. Несмотря на высокую информативность медицинских методов диагностики и их неоценимую пользу для решения широкого круга задач, они не предназначены для прогнозирования изменения показателей здоровья, в том числе с учетом влияния вредных факторов. Для количественной оценки поступления загрязняющих химических веществ и их влияния на организм человека (в том числе на органы дыхания), а также для исследования процесса дыхания как в норме, так и при наличии патологии авторами предлагается математическая модель дыхательной системы человека [4] .

Дыхательный аппарат человека представляет собой сложную биомеханическую систему, состоящую из разветвленной сети каналов, заканчивающихся альвеолами. За счет циклических упругих деформаций легких человека по системе движется воздух [5, 6] . Для изучения движения воздуха в верхних и крупных нижних дыхательных путях традиционно используются методы газовой динамики [4, 7 –9] , которые показали свою эффективность.

Моделирование движения воздуха по всей системе каналов вплоть до альвеол затруднено из-за сложности учета геометрии каждого отдельного канала (в легких взрослого человека содержится около 600 ^ 700 млн альвеол, а также соединяющих их каналов (диаметр каналов составляет 0.2 ^ 0.6 мм, альвеол — 0.2 ^ 0.3 мм [5, 10, 11] ). Прямое исследование движения воздуха в такой системе потребовало бы чрезвычайно больших вычислительных ресурсов. Для преодоления указанных трудностей в разрабатываемой математической модели дыхательной системы верхние и крупные нижние воздухоносные пути рассматриваются детально, а легкие

человека, образуемые мелкими дыхательными путями и альвеолами с содержащимся в них воздухом, считаются сплошной двухфазной циклически упруго-деформируемой насыщенной пористой средой [4, 12] . У легких, как пористой среды, довольно сложная внутренняя геометрия, поэтому для оценки характерного размера пор возможно использование отношения объема пор к площади их поверхности [13] . Относительное движение воздушной фазы в пористой среде легких описывается с привлечением теории фильтрации. Представление легких в виде пористой среды использовалось ранее в [14, 15] , но при этом не учитывалось взаимодействие легочной ткани и воздуха, содержащегося в легких; совместное решение задач деформирования легочной ткани и фильтрации не выполнялось. Иначе говоря, в цитируемых работах легкие полагались недеформируемой («пассивной») средой, через которую под действием перепада давления просачивается воздух. В настоящей работе предлагается рассматривать пористую среду как неоднородно деформируемую под воздействием движения грудной клетки и диафрагмы, создающих градиенты давления, обеспечивающие просачивание воздуха.

Фильтрация жидкостей и газов в пористых средах хорошо изучена в задачах подземной гидромеханики. Исследованиям в этой области посвящены, в частности, работы M.A. Био [16, 17] , Л.С. Лейбензона [18] , Г.И. Баренблата [19] . В задачах подземной гидродинамики обычно принимается гипотеза о слабой сжимаемости жидкости и недеформируемости скелета среды. В последние годы количество работ по данной тематике непрерывно возрастает [20] , что в значительной мере связано с потребностями нефтегазовой промышленности. В ряде работ приводятся постановки, в которых учитываются изменение пористости и проницаемости среды, обусловленные деформированием твердой фазы [21, 22] .

Легкие человека испытывают большие обратимые деформации (в процессе спокойного дыхания изменение объема составляет порядка 15%, в процессе глубокого — порядка 55%), в связи с чем для описания процесса деформации легких необходимо использовать соотношения нелинейной теории упругости. Предварительные исследования показали, что компоненты градиента перемещений в некоторых подобластях (особенно в примыкающих к диафрагме и грудной клетке) достигают 0.9 даже при спокойном дыхании, вследствие чего анализируемая в данной работе задача относится к классу геометрически нелинейных.

Общая структура математической модели дыхательной системы, состоящей из подмодели течения воздуха в воздухоносных путях, подмодели течения воздуха в деформируемой пористой среде легких, подмодели газообмена и подмодели регуляции дыхания с учетом взаимосвязей между подмоделями рассмотрена в [4] . Конститутивные соотношения, используемые для описания движения воздуха в пористой среде легких, приведены авторами в [12] . В связи с нелинейностью задачи ее аналитическое решение на настоящий момент представляется недостижимым; для решения предлагается применение численных методов и пошаговой процедуры с малыми шагами по времени. Для реализации алгоритма решения задачи требуется разработка комплекса программ. В настоящей работе в рамках построения общей математической модели дыхательной системы человека рассматривается только задача течения воздуха в легких человека, то есть совместная задача упругого деформирования пористой среды легких и фильтрации воздуха через деформируемую пористую среду. Приводятся необходимые разрешающие соотношения. Разработанный авторами алгоритм реализации и результаты, полученные с помощью представленной модели, остались за рамками данной публикации.

• 2.    Постановка задачи в дифференциальной форме

Дыхательная система человека (см. Рис. 1a ) моделируется совокупностью недеформируемой воздухопроводящей зоны, включающей носовую полость, глотку, гортань, трахею, пять генераций бронхов (указатель 1 )) и упруго-деформируемой респираторной зоны, включающей легкие, содержащие мелкие дыхательные пути и альвеолы (указатель 2 )). В легких человека сложно выделить отдельные каналы и альвеолы (Рис. 1б ); легкие человека, состоящие из мелких дыхательных путей, альвеол и воздуха в них, представляются двухфазной упруго-деформируемой насыщенной пористой средой, одна из фаз которой — деформируемый скелет среды (легочная ткань), моделируется как деформируемое твердое тело, вторая фаза — заполняющий поровое пространство газ.

Выделим представительный объем двухфазной среды (материальный объем двухфазной среды легких, в котором содержится достаточное для статистического описания число «носителей» дыхательного процесса), и возьмем его содержащим не менее 10 ³ альвеол.

Движение воздуха в воздухоносных путях в терминах газодинамики подробно изложено в предыдущих работах авторов [4, 9, 24] и в данной статье не обсуждается. Входами в легкие служат выходы из системы бронхов (Γ _AW/_L ). Связь между подмоделями воздухопроводящей и респираторной зон осуществим за счет задания условий на границе Γ _AW/_L . При рассмотрении задачи движения воздуха в деформируемой пористой среде легких на границах, являющихся выходами из системы бронхов/входами (Γ _AW/_L ), через которые воздух попадает в

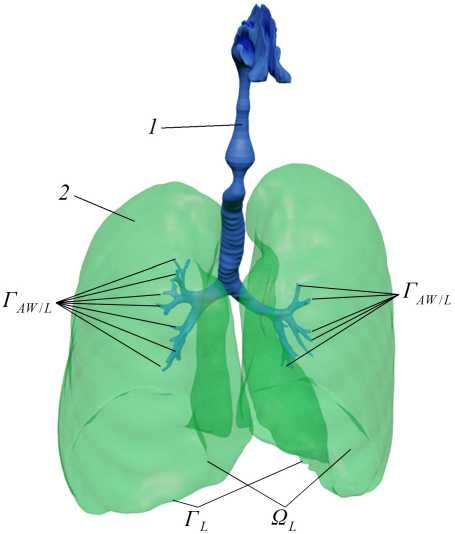
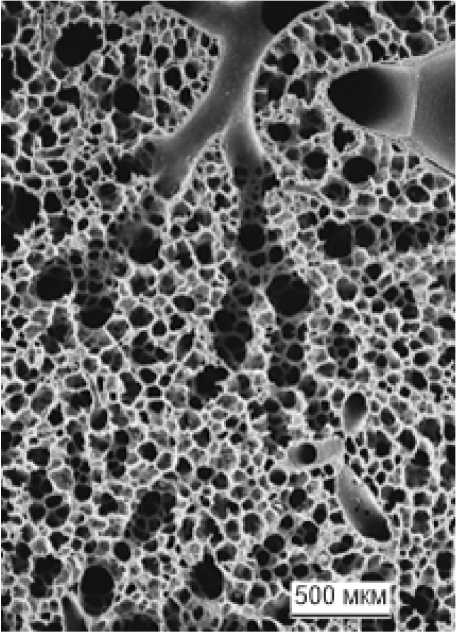
Рис. 1. Модель дыхательной системы ( а ), состоящая из воздухопроводящей зоны (указатель 1 ) и легких, аппроксимированных пористой средой (указатель 2 ); увеличенный фрагмент терминальных бронхиол, заканчивающихся альвеолами [23] ( б )

легкие, зададим силовые граничные условия, на стенках легких (Γ L ) — граничные условия кинематического типа (перемещения точек каркаса и условия непроницаемости для газовой фазы).

В качестве начального отсчетного состояния дыхательного цикла выберем момент «конец выдоха — переход к вдоху»; при обычном дыхании инерцией потока воздуха можно пренебречь. Скорости движения частиц воздуха в начальный момент времени приравняем нулю. В силу низких скоростей движения воздуха в воздухоносных путях и его малой вязкости на входах в легкие можно принять давление равным атмосферному. Данное состояние полагается естественным ненапряженным, компоненты шаровой и девиаторной частей тензора напряжений твердой фазы равны нулю. Отсчетная конфигурация (форма легких) восстановлена на основе томографических снимков и представлена на Рис. 1a . Начальные значение параметров зададим исходя из известных экспериментальных данных [10, 25 –27] : долю газовой фазы (пористости) примем равной 0.85; проницаемость — 1.58 · 10 ^-9 м ² [15] . В алгоритме реализации модели перед началом расчетов с указанными начальными значениями параметров отдельных фаз следует определить начальные характеристики двухфазной среды.

Дыхание — процесс нестационарный, в общем случае связь между подмоделями должна осуществляться в каждый момент времени в течение всего дыхательного цикла. Из решения задачи деформирования двухфазной среды легких определим поля скорости частиц газа в сечениях входов в легкие. Данное поле используем в качестве граничного условия для задачи газовой динамики в воздухоносных путях. В результате решения задачи для воздухоносных путей получим полное решение для скоростей движения воздуха и давления.

В первом приближении для компактного рассмотрения модели легких, не затрагивая задачу течения воздух в верхних дыхательных путях, в силу малой вязкости воздуха (то есть близости к идеальному газу, для которого в состоянии покоя в каждой точке сообщающихся сосудов давление одинаково), в подмодели движения воздуха в легких примем давление на границах выходов из системы бронхов (Γ _AW/_L ) равным атмосферному (касательные компоненты вектора напряжений будут нулевыми) на протяжении всего дыхательного цикла. В ходе решения задачи исследования течения воздуха в пористой среде легких человека определим законы изменения массовых расходов воздуха в течение дыхательного цикла, которые используем в качестве граничных условий для подмодели течения воздуха в проводящей зоне. При этом информацию о составе вдыхаемого воздуха для подмодели легких найдем из подмодели проводящей зоны.

Описание функционирования легких в процессе дыхания сводится к решению совместной задачи упругого деформирования двухфазного континуума (насыщенной пористой среды), состоящего из легочной ткани и воздуха, и фильтрации (относительного движения) воздуха через деформируемую пористую среду. Поведение первой фазы (легочной ткани) при деформировании зависит от ее упругих свойств, объема, плотности; в соотношения для описания фильтрации второй (газовой) фазы входят плотность, объем, давление, вязкость, температура, молярная масса, а также проницаемость легочной ткани. При расчетах по значениям параметров отдельных фаз определяются характеристики двухфазной среды. Все параметры напряженно-деформированного состояния и конфигурации легких, заполненных воздухом, а также параметры, учитывающие взаимодействие газа (воздуха) и легочной ткани, используются в подзадаче деформирования двухфазной среды, параметры газовой фазы — в подзадаче фильтрации.

Опишем фильтрацию законом Дарси; при этом естественно возникает вопрос о его применимости для рассматриваемого процесса. Объем легких человека может варьироваться от 3.5 до 7 л (от 0.0035 до 0,007 м ³ ), площадь газообменной поверхности — от 80 до 130 м ² . Размер пор (d), определенный как отношение объема пор к площади их поверхности, можно оценить в диапазоне от 2.69 · 10 ^-5 до 8.75 · 10 ^-5 м. При указанном размере пор, плотности воздуха p f = 1.1455 кг/м ³ (при температуре, близкой к температуре человеческого тела, t = 35°C), вязкости ^ f = 18,6 • 10 - 6 Па ^ с, скорости газовой фазы от 0 до 15.540 - 3 м/с характеризующие фильтрационное течение числа Рейнольдса (Re = p f U f d/^ f ) находятся в диапазоне от 0 до 0.08, что значительно меньше единицы [13] . В связи с этим применение закона Дарси для моделирования процесса фильтрации воздуха в пористой среде легких правомерно.

Для решения совместной задачи введем жесткую подвижную систему отсчета и свяжем ее с человеком. Будем рассматривать движение материальных объектов (частиц твердой и газовой фаз) только во введенной подвижной системе отсчета, считая ее инерциальной лабораторной системой координат (ЛСК). Воспользуемся лагранжевым подходом к моделированию: перед началом каждого временного шага будем переопределять у частиц лагранжевы координаты и отождествлять их с координатами в декартовой ортогональной ЛСК. Воздух в процессе дыхания перемещается в двух случаях: во-первых, вместе с двухфазной средой легких и, во-вторых, внутри пористой среды за счет перепада давления, обусловленного изменением объема легких.

Задача деформирования двухфазного континуума является существенно нелинейной за счет больших градиентов перемещений, поэтому ее постановка включает нелинейные уравнения движения (равновесия) и определяющие соотношения для расчетной области, занимаемой исследуемым континуумом и непрерывно изменяющейся. Решение подобных нелинейных задач осуществляется обычно или в скоростях, или в приращениях [28] . Общая постановка краевой задачи течения воздуха в упруго-деформируемой пористой среде, аппроксимирующей легкие человека, содержит следующие соотношения [12] :

– уравнение равновесия в скоростях (в предположении отсутствия внутренних массовых сил)

• V•« -V • (v •V о) = 0, r е Ml;(1)

  – соотношение для скорости изменения взвешенного тензора напряжений Кирхгоффа (в предположении изотропии упругих свойств твердой фазы и пренебрежении сдвиговыми напряжениями в газовой фазе)

S ^ avI+2^d7s+Qiog •S- S •Oiog;

– соотношение для тензоров деформации скорости и вихря

D =2(V v+V vT), w =j(V VT -V v);

– соотношение для девиатора тензора деформации скорости d = D - 1 I1(D)I;

– соотношения, связывающие взвешенный тензор напряжения Кирхгоффа Σ и тензор напряжения Коши σ двухфазной среды [29, 30] :

S = (p/p)o, о = (p/p)S;

– соотношение для скорости изменения среднего напряжения в терминах тензора напряжений Кирхгоффа двухфазной среды, учитывающее взаимодействие газа и легочной ткани, полученное аналитически на основе решения вспомогательной задачи о всестороннем сжатии/растяжении представительного объема двухфазной среды в форме шара, заполненного воздухом, для геометрически линейного случая (и впоследствии проверенное численно в геометрически нелинейной постановке при умеренно больших изменениях объема) [12, 31]

^S av = I 1 ( ^D )^Z,

z =(P/p)[AY f +B] ^-1 [AB(1 - Y f )(1 - -3/YTp -Cp f (Y f +1)] -

— (P/P^AY f + B] ^-2 [A+B][AB(1 - Y f )(1 - 3/Y/P>)-CY f P f ] + (P/P) 2 [AY f + B] ^-1 Cp f ;         (8)

– соотношение для логарифмической коротационной производной логарифмической меры деформации [32 –34]

Ω

H log = H - « log • H + H • Q iog = D ;

- соотношение для компонент логарифмического спина в базисе главных векторов p i (осей) меры Генки ( Н)

^ logij — W ij ⁺

^А 2 +^A 2

M^A i ^/A j ) ^A 2 ^{- A} 2

I D ij , ^A i = ^A j , i = j,

■^ logij = W ij , A i = A j , i= j;

– соотношение для определения тензора логарифмических деформаций через тензор Альманси

H =XH i p i p i =

₂E^ln ( ^{1 - 2 A} i ) p p i ,

A =1( V u + V u ^T -V u •V u ^T ) = XA i p i p i ,

где поле перемещений находится интегрированием поля скоростей перемещений; – соотношение для скорости изменения тензора деформации Альманси [28]

a = ₂(^V v + V v ^T ) - ( V v • A + A ^V v T );

• - соотношение для определения собственных значений правого тензора искажений V = ( V v • V v ^T )   через

собственные значения тензора Альманси

Ai = (1-2Ai)-1/2;

– закон сохранения массы газовой фазы

∂ dt(YfPf) + V•(Pfuf) = 0, rG^l, tG (0;T];

– соотношение для скорости фильтрации газовой фазы, полученное из закона Дарси,

k ( H )

Uf =--^V(pf), r €^l, tG (0;T];

µ f

– уравнение состояния для давления pf=MfR^f, rе^ tg(0;t];

– начальные условия

V •o0 = 0, r G ^L, t = 0;

n^o0 • n=PAW = pAtm, n •o0 - (n • o0 ^n)n = 0, r G rAW/L, t = 0;

u = u0, r G QL, t = 0;

p0f = pAtm, r e Ql, t = 0;

– граничные условия для двухфазной среды v = vrL, r e rL, t e [0;T);

n.«-(Vv•n^o+^Vv-n)n-о = T, r erAw/L, te [0;T);

– граничные условия для газовой фазы в подзадаче фильтрации pf\^w/l = pAtm, r e rAW/L, t e [0;T);

VfnlrL =0, r e rL, te [0;T).

В выражениях (1)–(25) приняты обозначения: σ — тензор напряжений Коши двухфазной среды; v — скорость частиц двухфазной среды; ∇ — оператор Гамильтона, определенный в актуальной конфигурации; Σ — взвешенный тензор напряжений Кирхгоффа двухфазной среды; Sav — скорость изменения среднего напряжения Кирхгоффа двухфазной среды; I — единичный тензор второго ранга; µ — второй параметр Ламе твердой фазы; d— девиатор тензора деформации скорости; 7s — объемная доля твердой фазы; Qlog — логарифмический спин; S — девиатор тензора напряжений Кирхгоффа твердой фазы; D — тензор деформации скорости; W — тензор вихря; р, р — плотность двухфазной среды в отсчетной и текущей конфигурациях; A = (2^+3а), B = 4^, C = (6^+3а), а, ^ — параметры Ламе твердой фазы; Yf — объемная доля газовой фазы; pf — давление газовой фазы, [Па]; Н — тензор деформации Генки, определенный в актуальной конфигурации; верхний индекс Ωlog — обозначение логарифмической коротационной производной; λi — собственные значения тензора искажений, Hi — главные значения тензора логарифмических деформаций H; Ai — главные значения тензора деформации Альманси; pi — главные векторы меры V; ρf — плотность газовой фазы; uf — скорость фильтрации газовой фазы в пористой среде (uf = Yf vf); vf — относительная скорость движения газовой фазы в пористой среде; k(Hi) — тензор проницаемости (второго ранга) пористой среды, [м2]; µf — динамическая вязкость, [Па·с]; R — универсальная газовая постоянная; θf — температура газовой фазы; Mf — молярная масса газа; pAW — давление на входе в легкие; pAtm — атмосферное давление; ΩL — замкнутая область двухфазной насыщенной пористой среды легких человека, QL — внутренность области легких, rL — граница области легких (QL = QL UrL UrAw/L); ΓAW/L — границы выходы из воздухоносных путей, являющиеся одновременно входами в легкие человека (граница между областями воздухоносных путей и двухфазной пористой средой легких rAw/L = QawAQl).

Скорость частиц двухфазной среды находится через скорости движения частиц каждой из фаз как среднемассовая скорость смеси. В силу того, что масса газа, содержащегося в рассматриваемом представительном объеме двухфазной среды легких, пренебрежимо мала по сравнению с массой частиц в нем твердого каркаса, скорость двухфазной среды можно считать совпадающей со скоростью твердой фазы ( v = v s ). Скорость движения частиц воздуха можно выразить в виде суммы скорости «переносного» движения — движения вместе с деформируемой твердой фазой относительно введенной лабораторной системы координат в рассматриваемой точке, и скорости «относительного» движения, обусловленного просачиванием газа относительно твердого каркаса. Таким образом, во всех определяющих и кинематических соотношениях скорость и перемещение частиц двухфазной среды полагаются совпадающими со скоростью и перемещениями частиц твердой фазы.

• 3.    Постановка задачи в обобщенной (слабой) форме

Ввиду того, что аналитическое решение нелинейной системы уравнений (1) – (25) в настоящее время не представляется возможным, для исследования процесса течения воздуха в пористой среде легких применяются численные подходы с использованием пошаговой процедуры. При решении нелинейных задач численными методами обычно осуществляется переход к обобщенной (слабой) форме, позволяющей понизить порядок дифференциальных операторов исходной (классической) постановки, ослабить требования к гладкости искомых переменных (перейти от пространства непрерывно дифференцируемых функций к пространству кусочно-дифференцируемых функций). Для получения обобщенного решения в механике сплошной среды широкое распространение нашли вариационные принципы [29, 35 –37] . Обзор вариационных формулировок геометрически нелинейных задач содержится в [38, 39] . Применение вариационных принципов для решения геометрически нелинейных упругопластических задач рассмотрено в [40] . Другим широко распоространенным подходом к формулировке обобщенных решений краевых задач является метод Галеркина [41 –44] , не требующий наличия вариационного принципа.

Для численного решения нелинейной подзадачи деформации двухфазной среды легких используется метод конечных элементов (МКЭ). Выполняется пошаговая процедура, то есть весь интервал нагружения разбивается на ряд малых шагов по времени. На каждом временном шаге последовательно рассматриваются две подзадачи: деформирование легких и фильтрация (относительное движение) воздуха через пористую среду. Ниже приведены разрешающие соотношения этих подзадач.

Умножим скалярно соотношения (1) и (23) на вектор-функцию h € H 1 (H 1 = {h G H ¹ (^ t )} — пространство Соболева), проинтегрируем по Ω и Γ _AW/_L соответственно:

J h - [ V- o -V • ( v -V o )]d^ = 0,

Ω

h - [ n - o — ( V v - n ) - o +( n -V v - n ) n - o - T] dr Aw/L = 0.                      (27)

Γ AW/L

Опустив часть выкладок (они приведены в [45] ), из соотношений (26) и (27) получим следующий итоговый вид обобщенного решения для двухфазной среды легких [45] :

I (V h ) ^T -- (P/P)

Ω

1                             1

I 1 (₂(V v +v v ^T ))Z I — I 1 (₂(V v +V v ^T )) S +

+2^

1,^                 1    ,1,^

2⁽v v +v v ^{T ) —} з I i ⁽ 2⁽v v + ^{v v T )} ) ij v s

d^+

+У(v h ) ^T -- (p/p) Ω

- ( V v ^T - S —V v - S — S -V v ^T + S -V v ) —V v ^T - S + ( V- v ) S

d^+

+У (V h ) ^T -- [ ( P/p ) [ Q --V v - S — S - Q --V v ]]d^ + у h - [ — T (V- v ) + ( n -V v - n ) T ]dr_AW/L =

Ω

Γ AW/L

= / h ^- [ ^T ]d^r AW/L .

Γ AW/L

Здесь тензор четвертого ранга Q имеет вид:

Q= i,j,m,n,q,k

1, ln(X q /X k )

^X 2 ^{+ X} k λ q ² - λ ² k

l i^q l j^k k ⁱ k ^{j l qm}

l kn ⁺ l km l qn k m k n

,

где l ij , l _j ⁱ — соответствующие компоненты матрицы косинусов углов между базисными векторами k i ЛСК и главными векторами p j меры тензоров искажения V (совпадающими с главными векторами тензоров Альманси и Генки) определяются согласно соотношению: l ij = l j = k i - p j . Переменная Z в (28) учитывает влияние давления воздуха, находящегося в пористой среде легких, на скелет среды (легочную ткань), и вычисляется из (8) по давлению газовой фазы, пористости двухфазной среды и упругим свойствам легочной ткани.

Соотношение (28) представляет собой обобщенное решение исходной задачи, из которого устанавливаются скорости движения двухфазной среды легких и параметров деформирования двухфазной среды. Численное решение подзадачи деформирования двухфазной среды легких осуществляется на основе соотношения (28) с использованием МКЭ [46] . Прежде чем перейти к разрешающему соотношению в терминах КЭ, запишем (28)

в компонентной форме:

У h j,i (р/р) 3 Zv k,k S j + p(v j,i +V i,j )7 s

µv k,k γ s δ ij

^

- 3 V k,k Z ij

dQ+

Ω

+jh j,i ^{( P/P )} ^(vil S ij

^{— v} l,i S lj -S ik ^v k,j + S ik ^v j,k ) -v i,l ^ lj +v k,k B ij

dQ+

Ω

+/ ^{h j,i} [(^p/^p) h_ Q^ ^lk S sj v ^l,k - ^{Q pjlk S ip V l,k}]] M + I h i [ ^{- T} i v ^k,k + ^{v i,k} n ^k n l T i ] ^dr A^w/L =

Ω

= I hi [T i ]

Γ AW/L

Γ AW/L dΓ AW/L .

Рассматриваемая область представляется совокупностью M тетраэдральных конечных элементов. С использованием функций формы запишем итоговый вид разрешающего соотн оше ния в подзадаче деформирования двухфазной пористой среды легких человека для КЭ с номером m (m =1 ,M ):

M x Z m=K/ n(m)

(P/P)

_R ^(m)r B _jjα

17 _R ^{( m )} q i гттУг.Л omqq, rmmrr ~ _R(m)q_ _R(m)r ²,', _R^{( m )} q 3 ZB kke ^{+ B} jia ^ f s B jie ⁺ B jia ^f s B ij^    B jja g ^I s B kkp

i _R ^(m)r 2p r mqq 'B jia з ^ 'j B kke

m^m )

(P/P)

_R^(m)r Ip f mi-qq

B jia 2 S ^kj B ike

, ^{( m)}r Ip r m nqq ' jia 2 S ^kj B kie

( n ) r B jiα

• ¹    p. _R^{( m )} q । rmt ™) ^{1 1} p. in"4q _R ^{(m )} r p . r mqq 2 S ^ik B kje 'B jia 2 S ^ik B jke B jia ^ ^kj B ike

  d& m p m ) '+

  
  

M

_l_J X / (z / m\ ip^^ p p R^{( m)q}  D^(m)r p p D^(m)q"|j o(m) Ь^Л,(т)в I + 1 2_^ / ^(P/P) [B jia Q iplk S pj B ike    B jia Q pjlk S ip B lke J d^    |vq '

m=1

n ^{( m )}

M Γ

( n ) r           ( n ) q      ( n ) q                 ( n )

+ L / Nia  [-TBkkkf 'Blk/nnk nlTi\ drAW/L m 1 (3)

Γ AW/L

M Γ

( m )

Γ AW/L

( n ) r N iα

( n ) dΓ AW/L

где приняты обозначения: индексы в виде греческих букв α и β — номера узлов, в виде латинских букв — координатные оси; N iemj — функции формы (N m ) ( r e ) = 0 при а = в, N iemi ( r e ) = $ i , i,j = 1,3); B jnp¹ ( r ) = dN ^m¹ ( r ) / dx^l —производные функций формы; v jm)¹³ —вектор узловых скоростей. Связь компонент скоростей перемещений внутри элемента, компонент градиента вектора скорости со скоростями перемещений в узлах с учетом функций формы имеет вид:

p i^m) = N in ( r ) v qm ^{) e} , V im = Nip ( r ) v qm ^{) e} .

Ненулевые диагональные элементы функции формы Nim^^q определяются через координаты узлов из соотношений [41] :

• ( n )    ( n ) ( n )        ( n ) ( n )        ( n ) ( n )

N (m)q = ^а в ^{+ Ь} в x i = q =1 ^{+ С} в x i = q =2 ⁺ d e x i = q =3 ^П i ^e =                   6V ( m )                   .

Здесь в есть I , J , K , L — номера узлов рассматриваемого тетраэдрального четырехузлового элемента; x ^ m , x j m , xj m —координатные оси; V ^{( m )} — объем КЭ; а вт ) b^' ) , C pm , d em —коэффициенты.

Объем тетраэдрального КЭ (он же объем содержащейся в нем двухфазной среды ) и коэффициенты a, b, c, d (например, для узла I) находятся как определители матриц (индекс элемента (m) опущен):

1 X1I    X2I 3I V= = - det 1  X1J   X2J   X3J 6 1 X1K  X2K  X3K 1 X1L   X2L   X3L X1J X2J X3J 1 X2J   X3J а I = det V1K x2K x3K , bI = -det 1 X2K  X3K X1L X2L X3L 1 X2L   X3L x1J 1   X3J X1J X2J   1 ci = -det x1K 1 x3K , dI = -det X1K X2K  1 X1L 1 X3L X1L X2L   1 где xqβ — координаты узлов; коэффициенты для остальных узлов получаются циклической перестановкой индексов I, J, K, L.

На основе соотношения (29) с помощью процедуры ансамблирования формируется матрица жесткости и вектор правой части; формируется система линейных алгебраических уравнений (СЛАУ), из решения которой устанавливаются векторы скоростей узлов сетки, аппроксимирующей область двухфазной пористой среды.

Для моделирования относительного движения воздуха в пористой среде легких применяется метод конечных (контрольных) объемов (МКО), который хорошо зарекомендовал себя при решении задач механики жидкости и газа [47, 48] . В качестве контрольных объемов (КО) будем использовать те же элементы, что и при решении подзадачи деформирования. Давление газовой фазы, найденное через изменение объема, привяжем к центрам КО; значения вычисляемых переменных (средние значения по КО) в подзадаче фильтрации будем определять в центрах КО.

Подставим соотношение (16) в (15) и проинтегрируем по m-му контрольному объему ^ ^{( m )} :

∂ j  dt (YfPf ) + ^

(    k ( HH )     A

^-pf~— '^(p f ) µ f

d^ ^m =0.

С помощью теоремы Остроградского–Гаусса преобразуем соотношение к виду:

I [ dt ^{( Y f Pf} )]d"^w + / [("^P f ^{k H} \   ))]

n dS ^(m) = 0,

П(т)                            S(m) L '                       ' J где S(m) — ограничивающая КО поверхность, n — внешняя нормаль к ней.

Для численной реализации разрешающего соотношения (30) выполним аппроксимацию по времени и пространству:

^{( n )}_ ^{( n -1)}

(n - i) ^P f     ^P f

γ f       ∆t

v ^{( n -i)} ₊y^

^{( a )}

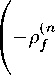
( n - i)     ( n - i)   ( n - i)

1) k (U) p fA ( a ) - p fC     e CA ( a )

^ f        e^{(n -1)}        e^{(n -1)}

| e CA(a) |     | e CA(a) |

(n - 1) (n - 1) n (a)    S (a)

= 0.     (31)

При этом ∆t — шаг по времени подзадачи фильтрации; (n) — индекс, указывающий на текущий момент времени t n ; индексы C и A обозначают, соответственно, центры рассматриваемого и соседнего элементов, имеющих общую грань (a); e cA ( _a ) — вектор, соединяющий центры текущего и соседнего элементов; n (_a) — единичный вектор внешней нормали к грани (а) контрольного объема; S (_a) — площадь грани (а) контрольного объема (при этом учитываем, что тетраэдральный элемент имеет четыре грани).

Из соотношения (31) получим выражение для определения плотности газовой фазы в КО:

о^{( n )} -X

P f =

(a)

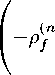
(n - 1)     (n - 1)   (n - 1)

1) k (U) p fA(a) -p fC    e CA(a)

M f         e^{(n -1)}        e^{(n -1)}

| e CA(a) |     | e CA(a) |

(n - 1) (n - 1) n (a)    S (a)

∆t

Y f ^{n -1)} V (n - 1)

(n - 1)

.

На основе соотношения (32) устанавливается изменение плотности газовой фазы в КО пористой среды легких за счет изменения их объема, поступления/оттока массы (между соседними элементами или через границы (грани) Γ _AW/_L , являющиеся выходами из воздухоносных путей и одновременно входами в легкие), обусловленного градиентом давления газовой фазы.

Таким образом, движение воздуха в легких человека в процессе дыхания описывается в виде связанной задачи упругого деформирования двухфазной насыщенной пористой среды (см. разрешающие соотношение (28) ) и фильтрации воздуха в пористой среде (см. соотношение (32) , при этом входящие в него переменные, зависят от решения подзадачи деформирования двухфазной среды легких). В результате деформирования изменяются координаты узлов, объем элемента (V ), площади граней (S), нормаль к граням ( n ), координаты центров элементов и расстояния между ними. В зависимости от объема другой становится пористость (доля газовой фазы) и давление газовой фазы в элементе. Давление воздушной фазы зависит от двух составляющих: от изменения объема на каждом шаге деформирования (определяется из подзадачи деформирования) и от изменения плотности воздушной фазы (при этом производная давления прямо пропорциональна производной плотности (см. соотношение (17) ), находимой из решения подзадачи фильтрации. Результаты, получаемые из подзадачи фильтрации, в свою очередь, оказывают влияние на решение подзадачи деформирования: давление газовой фазы, которое зависит от результатов решения подзадачи фильтрации, входит в соотношение для скорости изменения среднего напряжения двухфазной среды легких (см. соотношения (7) , (8) ).

В связи с нелинейностью задачи ее решение осуществляется пошагово. Для реализации связанной задачи деформирования пористой среды и фильтрации воздуха в ней возможны два варианта построения алгоритма: либо объединить подзадачи деформации и фильтрации в одну систему уравнений [49, 50] , которую решать на каждом временном шаге, либо на каждом временном шаге последовательно решать каждую из подзадач [51 –54] . Авторами выбран второй вариант: сначала будем решать подзадачу деформирования двухфазной среды в скоростях (с использованием МКЭ), при этом все характеристики газовой фазы (включая поровое давление и пористость) принимаются постоянными и соответствующими началу текущего шага по времени; далее будем решать подзадачу фильтрации (с использованием МКО). По найденным скоростям изменения искомых параметров интегрированием вычислим значения параметров (компонент тензоров напряжений и деформаций, векторов перемещений узловых точек, переопределим конфигурацию области) и примем их за исходную информацию для решения на следующем временном шаге.

• 4.    Заключение

В работе предложена модель для исследования течения воздуха в легких человека, в которой последние моделируются как упруго-деформируемая насыщенная двухфазная пористая среда. Представлена общая структура модели с учетом за счет граничных условий взаимосвязи подмоделей воздухоносных путей и легких. Сформулирована математическая постановка нелинейной задачи. Решение задачи предполагает рассмотрение подзадач деформирования пористой среды легких и относительного движения воздушной фазы в пористой среде, связанных через искомые переменные. Решение подзадачи деформирования осуществляется методом конечных элементов, подзадачи фильтрации — методом конечных объемов; получены разрешающие соотношения МКЭ и МКО. В связи с нелинейностью задачи ее решение предполагается осуществить с помощью пошаговой процедуры. Для численной реализации решения требуется разработка алгоритма и комплекса программ, описание которых и анализ результатов остаются за рамками данной публикации.

Исследования выполнены при финансовой поддержке Министерства науки и высшего образования Российской Федерации (проект № FSNM-2023-0003).