Моделирование технологических процессов на прошивном прессе трубопрессовой линии

В мировой практике производства бесшовных горячекатаных труб из малопластичных нержавеющих сталей и труднодеформи-руемых сплавов широкое применение находят процессы горячего прессования [1–6].

Условия функционирования оборудования для производства бесшовных стальных труб и особенности реализации современных технологических процессов на трубопрессовых линиях установили определенные приоритеты в данном направлении. При этом повышение эффективности технологических процессов прошивки сплошной или экспан-дирования предварительно сверленной трубной заготовки путем совершенствования как технологии производства, так и модернизации оборудования прошивного пресса выдвигают ряд актуальных задач. К ним относятся: выбор рациональных решений, связанных в конечном итоге с оптимизацией качества бесшовных горячекатаных труб; отработка требуемых технологических характеристик; прогнозирование показателей стойкости технологического инструмента и надежности функционирования трубопрессового оборудования. Данные вопросы диктуют кардинально новые подходы к рассматриваемой задаче.

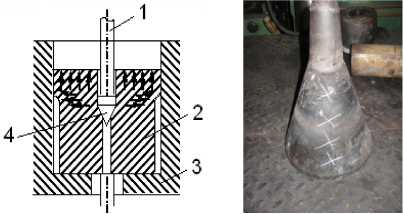
Очевидно, что прогнозирование существующих и разработка новых технологических процессов производства горячекатаных труб в рамках данной задачи указывают на необходимость создания корректных математических моделей технологических процессов, адекватно отражающих условия прошивки или экспандирования трубных заготовок на современных прошивных прессах трубопрессовых установок (рис. 1).

Необходимо подчеркнуть, что при прошивке или экспандировании предварительно просверленных трубных заготовок из трудно-деформируемых сталей и их сплавов для уменьшения сил трения в очаге деформации и стабилизации самого технологического процесса используются различные приемы. Например, чистоту и качество поверхности при прессовании труб из малопластичных материалов обеспечивают применением специальных технологических смазок. Для этой цели, как правило, в промышленных условиях преимущественно применяют различные порошки, смазочные шайбы, жидкую или стекловидную смазку. Однако данные мероприятия коренным образом не устраняют узкие места при производстве высококачественных труб.

а)                            б)

Рис. 1. Схема технологического процесса экспандирования трубной заготовки (а); картины износа экспандера (б), контейнера (в); оправка (г) вертикального прошивного пресса 12 МН фирмы SMS MEER трубопрессовой линии. 1 – стержень (игла); 2 – трубная заготовка; 3 – контейнер; 4 – экспандер (оправка)

в)

0100       /

г)

Отметим, что вследствие несовершенства формы образующей рабочей поверхности оправки или экспандера в процессе прошивки или экспандирования трубной заготовки она подвергается интенсивному износу обтекающим потоком горячего металла. Преимущественно это приводит к существенному увеличению осевого сопротивления оправки или экспандера, изменению прямолинейного устойчивого положения поддерживающей иглы по оси прошивки и, как следствие, к ухудшению качества прошитых гильз.

Очевидно, что в данном случае на передний план выдвигается проблема оптимизации самого процесса прошивки или экспандиро-вания путем выбора рациональных параметров технологического процесса и инструментов, что неразрывно связано с развитием фундаментальных методов исследования очага деформации [1, 2]. Отметим, что нарушение проектных размеров полученных гильз вызвано, в основном, изменением геометрических размеров оправки или экспандера и в результате их интенсивного износа в процессе прошивки и дальнейшего искажения оси контейнера.

Реализация устойчивых процессов прошивки трубной заготовки с относительно высокими темпами деформации металла обуславливает разработку принципиально новых физических и математических моделей рассматриваемого технологического процесса, что в основном базируется на развитии результатов ранее проведенных исследований [3, 4].

Задача выбора параметров технологического инструмента для прошивки или экспан-дирования трубных заготовок с применением методов расчета калибровки в теоретическом плане недостаточно полно изучена и в ограни- ченном объеме изложена в ряде работ [5, 6]. В существующей литературе отсутствуют строгие рекомендации и однозначные предложения по выбору рациональных геометрических параметров технологического инструмента (калибровок экспандера или оправки).

Характерно то, что при отработке конкретных режимов прошивки или экспандиро-вания трубных заготовок на этапе проектирования технологических процессов возникают определенные трудности, обусловленные особенностями динамики функционирования очага деформации.

Целью данной работы является разработка практических рекомендаций по выбору рациональных параметров (калибровке) технологического инструмента путем создания динамической модели технологического процесса прошивки или экспандирования трубной заготовки. Ниже приведены наиболее значимые выкладки, где сделана определенная попытка получить корректную математическую модель процесса прошивки или экс-пандирования трубной заготовки на основе базовых положений динамической аналогии течения металла в очаге деформации.

В основу гидродинамического моделирования очага деформации с принятой реологией рабочей среды положены динамические процессы при прошивке или экспандировании трубной заготовки. Данная методика расчета характерна и особенно эффективна при высокоскоростной прошивке или экспандирования трубной заготовки на прошивном прессе. В этом случае требуется установить соответствие предложенной реологии рабочей среды и гидродинамической модели физическим и граничным условиям процесса прошивки или экспандирования металла на прошивном прессе.

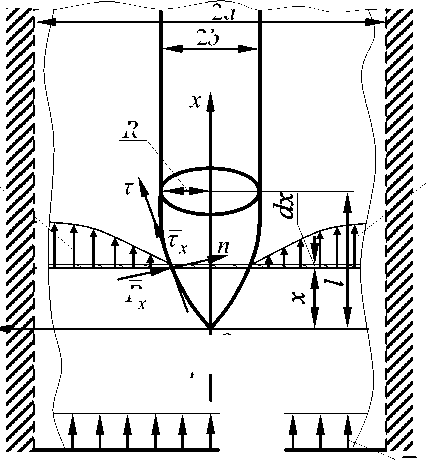
Очаг деформации прошивного пресса и динамические процессы прошивки сплошной или экспандирования сверленной трубной заготовки в гильзы требуемых размеров в дальнейшем моделируем на основе динамической аналогии очага деформации [5]. При этом обтекающий поток металла рассматривается как вязкопластическая среда (принятая реология), которая размещена в ограниченном пространстве осесимметричного очага деформации, образованном контейнером и оправкой или экспандером заданных геометрических размеров (рис. 2).

Следовательно, в рамках принятой вязкопластичной реологии рабочей среды и динамической модели технологического процесса удобно воспользоваться цилиндрической системой координат и фундаментальными уравнениями Навье – Стокса [3, 6]. После отбрасывания ряда второстепенных слагаемых дифференциальные уравнения Навье – Стокса для осесимметричной динамической модели процесса прошивки или экспандирования можно записать в виде:

dp = ^V2u r-U1; (1)

О r V r 2 )

d p

5 x

uV ² u x ,

где d2   1 d d2

—т +----+—ч dr 2 r dr dx 2

- обобщенный оператор Лапласа; ц - коэф- фициент вязкого сопротивления металла (рабочей среды); p – давление металла в очаге деформации; иr, иx - соответственно ради- альная и осевая составляющая скорости движения металла (рабочей среды) в очаге деформации.

Коэффициент вязкого сопротивления рабочей среды в данной постановке задачи определяется графическим дифференцировани- ем механических характеристик прошиваемого металла в напряженно-деформированном состоянии согласно [6].

Уравнение неразрывности при движении потока металла между контейнером и оправкой или экспандером в принятой постановке осесимметричной задачи с динамической моделью «вязкой» рабочей среды записывается в форме

^{d ( r и} r ) + 5 ( r U x ) = 0 d r      d x

В дифференциальных уравнениях (1), (2) и уравнении неразрывности потока металла (4)

следует учесть, что осевая составляющая ско- r

2 a

V ( x , r )

R

P

F

2 b

U ( x , r )

O

V

Рис. 2. Расчетная схема процесса прошивки сплошной или экспандирования сверленной трубной заготовки на прессе (процесс обтекания оправки или экспандера потоком металла)

рости движения металла намного превышает

радиальную составляющую и r « и x , следова- , д( и _г )

тельно, можно принимать и r = 0; ——- = 0.

O x

Это установлено существующими ограничениями границ очага деформации по контейнеру и оправке.

Если оправку или экспандер пресса в обтекающем потоке металла считать относительно «тонкой» ( Rjl ^ 1), то можно предпо-

кой или экспандером. На соответствующих границах данных технологических инструментов в процессе прошивки или экспандиро-вания имеет место

ul  = 1; и|--    = о,

I г = 1            1 г = R ( x )

где R ( x ) - уравнение образующей поверхно-

а(U(x г)) д( U(x, г)) ложить uY = U(x, г), что —------ « —------. x ex         дг

Тогда дифференциальные уравнения (1) и (2), в рамках данной реологии рабочей среды и предложенной динамической модели (при

— = 0), запишутся в виде преобразований д г

сти оправки или экспандера в данном сечении x очага деформации.

Из уравнения (7), используя условия взаимодействия металла с технологическими инструментами (8) (контейнером и оправкой или экспандером), соответственно определяем параметры интегрирования c 1 ( x ) и c ₂ ( x ) в

виде:

^c 1 ( x ) = 1 ^-

1 d p 4 d x ^;

Пуазейля [5]

d— (д U 1 д U — = Ц —у +-- dx    \дг ² г д г

c 2 ( ^x ) =

1     ^d — Г 1

4ln R ( x ) dx L

R ²

^{( x} ) ] .

Для определения градиента давления вос-

где U ( x , r ) – осевая составляющая скорости

течения металла в очаге деформации.

Для удобства решения задачи на базе динамической аналогии технологического процесса систему уравнений (5) представим в безразмерной форме

пользуемся условиями неразрывности потока металла в очаге деформации прошивного пресса в форме постоянства расхода рабочей среды. Учитывая условия течения металла между контейнером и оправкой или экспандером в очаге деформации, для квазиустойчи-

dp д и 1 д и

—= = ^_zy + = —”, dx д г г д г

pa где г = г/a; x = x/a; p = —; цо

U

U =--соот-

вого процесса уравнение неразрывности потока металла можно записать в следующей безразмерной форме

_J 2 Urdr = 1.                        (10)

R ( x )

ветствующие безразмерные параметры уравнения (6) и очага деформации в процессе прошивки или экспандирования; и - постоянная осевая составляющая скорости движения металла; а – радиус втулки контейнера.

Интегрируя дифференциальное уравнение (6), согласно [3, 4], с учетом постоянства градиента давления, получаем выражение для определения скорости течения потока металла в очаге деформации

U ( x , г ) = — ^Р Т 2¥ ² + c₁ ( x ) + c ₂ ( x ) In г , (7) 4 dx 1 2

где c 1 ( x ) и c ₂ ( x ) - параметры интегрирова-

Произведя соответствующие подстановки и ряд необходимых преобразований, из уравнения (10) с учетом (9) находим градиент давления в очаге деформации

dp = f . ^{R ( x} ) ^dx f 2 Г R ( x )

где f [ R (x )] = 2 R (x)-1;

f 2 [ ^R ( x ) ] =

1 - R ⁴ ( x )

ния задачи.

Воспользуемся соответствующими граничными условиями задачи в очаге деформации в виде характерных условий взаимодействия металла с втулкой контейнера и оправ-

-

x

1 rm 1—R3 (x )

1 - R ( x ) _

In R ( x )

2        4 R ( x ) In R ( x )

0,5 + R ²( x ) [ ln R ( x ) - 0,5 ] .

x

Интегрируя выражение (11) с известными граничными условиями задачи |p|x=j = 0, для ква- зистационарного технологического процесса прошивки или экспандирования трубной заготовки запишем интегральное уравнение для определения безразмерного давления в рассматриваемом сечении x очага деформации

И . Г R ( x ) " f—УУ4 dx .

Р (x ) = —( г- -. xf 2 [_ R (X )

Опираясь на ранее принятые условия стационарного течения металла в очаге пресса, касательное напряжение в рамках гидродинамической модели и принятой реологии процесса обтекания оправки или экспандера потоком горячего металла (рабочей среды) определяем согласно [5] из закона вязких трений Ньютона a и (r, x)

t(r,x 1 ц~

.

r = R ( x )

Следовательно, при определенных граничных условиях взаимодействия оправки или экспандера в обтекающем потоке горячего металла (вязкой среды) в процессе прошивки или экспанди-рования трубной заготовки имеет место

T =

t a _ dU ---или t = — ц V        d r

r = R ( x )

Используя выражение (7), находим касательное напряжение на рабочей поверхности оправки или экспандера (r = R(x)) в рассматриваемом сечении x очага деформации

^{t ( x} ) = I dp ^{R ( x ) +} c ^{2 ( x} )                                                                   ⁽¹⁶⁾

2 dx             R ( x )

После подстановки параметров интегрирования (9) и градиента давления (11) в уравнение (16) и незначительных преобразований окончательно найдем касательное напряжение на рабочей поверхности оправки или экспандера в виде:

• f R ⁽ x U R ( x ) +

T ( x ) = r—' '

2 f2 R ( x )

£     f[ R ( x ) ]

4ln R ( x ) f 2 [ R ( x ) ]

1 - R (x)

-

1            1

In R (x) R (x)

Осевое сопротивление оправки (сила прошивки) или экспандера (сила экспандирования) на прошивном прессе с учетом динамической модели процесса определяется из условия взаимодействия инструментов со сплошным обтекающим потоком металла в очаге деформации

l

l

F = (2nR (x) R'(x) p (x) dx + (2nR (x )t( x) dx,

где l – длина рабочего участка оправки или экспандера.

Для удобства решения задачи воспользуемся ранее принятыми безразмерными параметрами задачи. После подстановки (11) и (17) в выражение (18) осевое сопротивление оправки или экспандера представим в безразмерной форме

—   —  — i f R ( x )

F = —(R(x)R'(x) (21Ш xf2 R ( x )

l

11 f1ГR (x)

4 dx dx + (-- p__z :

I             0 ^{2 f} 2 ^{R ( x} )

R(x) +

+

f1 ГR (x)Jn ,2.-. — .1 1 - R (x )

^{4ln R ( x} ) ^f 2 Г ^R ( x ) 1L

—

ln R (x) R (x)

d x .

Сходимость интегрального уравнения (19) в целом обеспечивается тем, что соблюдаются основные условия сходимости отдельных слагаемых. Условия сходимости силы осевого сопротивления (19) указывают на то, что параметры процесса прошивки или экспандирования в рассматриваемом сечении x очага деформации устойчивы.

Осевое сопротивление оправки или экспандера в потоке металла окончательно определяется

F = 2 πµυ aF .

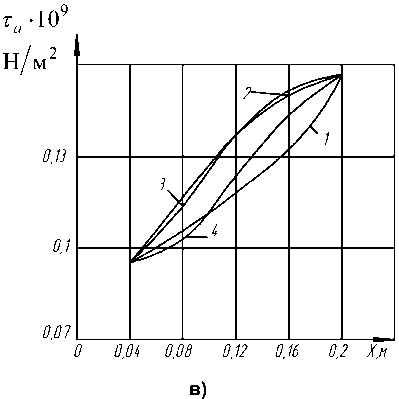
Далее, в первом приближении, для наиболее распространенных условий эксплуатации прошивного пресса, задаваясь определенной формой образующей оправки или экспандера, находим характер распределения энергосиловых параметров в очаге деформации. Кривые, приведенные на рис. 3, для некоторых наиболее распространенных или характерных форм образующих экспандера диаметром 90 мм прошивного пресса 12 МН, обуславливают распределение давления и касательных напряжений в очаге деформации и их изменение по всей длине рабочей поверхности образующих как экспандера, так и втулки контейнера.

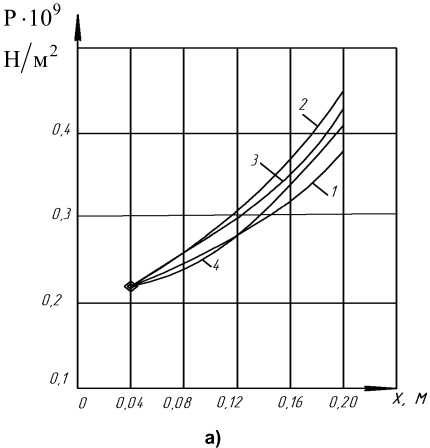
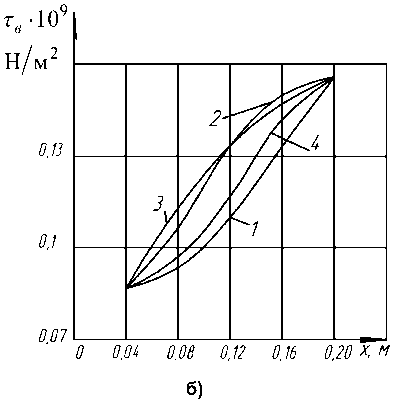
Рис. 3. Распределение давления металла и касательных напряжений в очаге деформации в процессе экспандирования круглых заготовок на прошивном прессе 12 МН фирмы SMS MEER (заготовка ∅ 180, экспандер ∅ 90, материал 12Х18Н10Т, µ = 6,8 ⋅ 10⁴ Па ⋅ с): а – распределение давления в очаге деформации; б – распределение касательных напряжений на поверхности оправки; в – распределение касательных напряжений на поверхности контейнера (принятые формы образующей оправки: 1 – конус; 2 – парабола; 3 – тор; 4 – кубическая парабола)

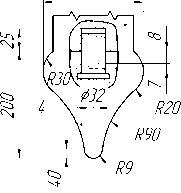
Путем моделирования процессов экспандирования трубной заготовки переходим к проектированию экспандера рациональной формы. В первом приближении путем подбора параметров и формы образующей экспандера минимизируем его осевое сопротивление обтекающему потоку металла. Например, для заданной формы образующей экспандера удобно минимизировать осевую составляющую усилия прошивки F на заданной длине оправки l . Поскольку радиус калибрующего пояска экспандера R известен, то исходим из условия необходимости образования

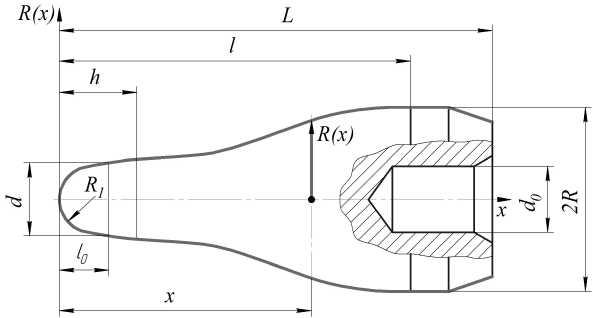
Рис. 4. Экспандер прошивного пресса 12 МН фирмы SMS MEER рациональной калибровки (бутылочнообразная форма)

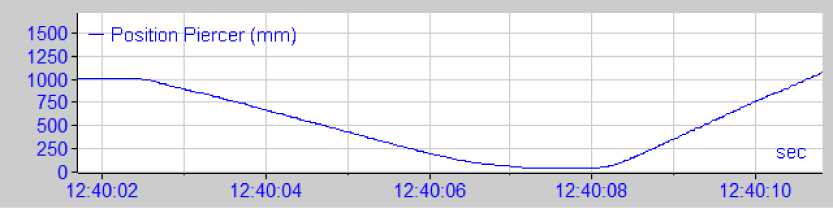
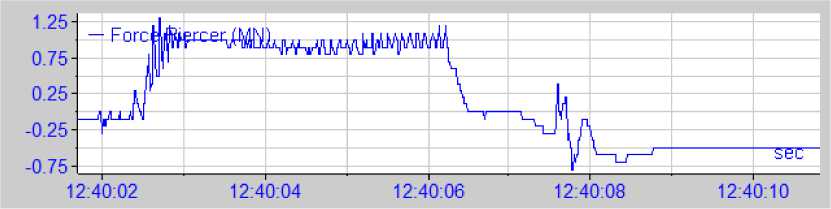
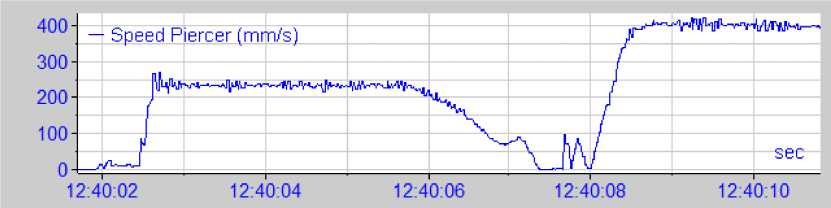
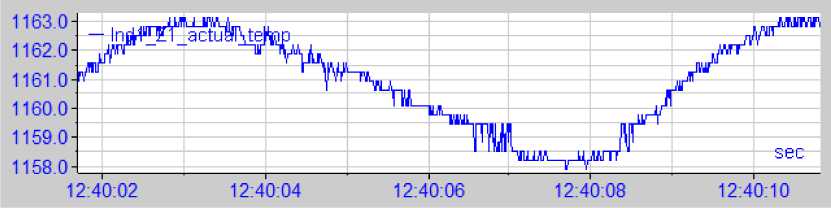
Рис. 5. Типовая осциллограмма процесса экспандирования предварительно сверленной трубной заготовки на прошивном прессе 12 МН фирмы SMS MEER трубопрессовой линии (заготовка ∅ 180 мм, материал 12Х18Н10Т, экспандер ∅ 90 мм)

полых гильз (труб) с требуемыми геометрическими размерами. Такой подход приводит к некоторому увеличению расчетной длины экспандера, что в ряде случаев обуславливает нарушение стабильности очага деформации. При этом одновременно путем минимизации функционала осевого сопротивления экспандера потоку металла достигнуто заметное повышение устойчивости процесса прошивки, что приводит к заметному снижению разно-стенности гильз.

Результаты исследования показывают, что экспандер диаметром 80 мм с формой образующей, соответствующей кубической параболе, при прочих равных условиях обеспечивает рациональное распределение давления металла и касательных напряжений по всей длине очага деформации в процессе экспан-дирования гильзы. Необходимо отметить, что через определенное время эксплуатации экспандера с конической образующей рабочая поверхность приобретает «бутылочнообразную» форму (рис. 4), которая по картине износа идентифицируется с некоторой кривой, приближенно совпадающей с кубической параболой. Очевидно, образующая рабочей поверхности оправки с течением времени приспосабливается к реальным условиям экспан-дирования. Полученные результаты удовлетворительно совпадают с экспериментальными данными, приведенными в работах [7, 8].

Уточнение решения задачи по оптимизации очага деформации возможно с применением одного из известных методов (метод Гаусса – Зейделя, Эйлера и др.) [3, 6]. При этом из условия минимума силы осевого сопротивления оправки или экспандера металлу в очаге деформации определяем рациональную форму образующей ее рабочей поверхности.

Идентификацией результатов диагностики технологического процесса экспандирова-ния трубной заготовки на прошивном прессе 12 МН фирмы SMS MEER трубопрессовой линии системой «ANALIZISIS» и методами математической статистики установим зависимость между энергосиловыми параметрами процесса и формой технологического инструмента (рис. 5).

Повышение эксплуатационной стойкости и снижение потребления дорогостоящих технологических инструментов (оправок или экспандеров) обеспечивается рациональным распределением энергосиловых параметров прошивки в очаге деформации и оптимизацией формы образующей рабочей поверхности.

Следует подчеркнуть, что путем моделирования необходимых условий течения металла в очаге деформации, на соответствующем этапе проектирования технологического процесса, назначаются рациональные режимы (устойчивые условия) прошивки сплошных или экспандирования сверленных трубных заготовок в гильзы заданных размеров.

• 1.    На основе фундаментальной теории гидродинамической аналогии и принятой реологии металла трубной заготовки предложена обобщенная математическая модель процесса прошивки или экспандирования трубной заготовки на прошивном прессе.

• 2.    Определены энергосиловые параметры в процессе прошивки или экспандирования трубной заготовки. Для квазистационарных условий реализации технологического процесса и осесимметричного очага деформации определены: давление металла, касательные напряжения и сила осевого сопротивления оправки потоку металла.

• 3.    Установлен функционал осевого сопротивления оправки обтекающему потоку металла, что позволило моделировать и обеспечивать необходимые условия реализации устойчивых технологических процессов на прошивном прессе.

• 4.    Исходя из условия минимума функционала осевого сопротивления оправки в обтекающем потоке металла, предложена рациональная форма образующей рабочей поверхности (калибровка) оправки или экспандера.