Моделирование технологического процесса сборки авиакосмических изделий из трехслойных конструкций с помощью резьбовых вкладышей

Самарский государственный аэрокосмический университет

Описана математическая модель процесса сборки изделий авиакосмической техники, выполненных из трехслойных конструкций с помощью резьбового вкладыша. Модель определяет энергосиловые параметры и перемещения по внешнему контуру резьбового вкладыша при его осевом пластическом сжатии. Математическая модель позволяет спроектировать технологический процесс образования отверстий с резьбой при сборке трехслойных конструкций и выбрать оборудование, необходимое для его осуществления.

Одним из основных требований при проектировании трехслойных конструкций является их минимальная масса при обеспечении достаточной прочности и жесткости.

Существенные отличия физико-механических свойств этих конструкций от аналогичных свойств традиционных материалов и сплавов обусловлена тем, что они хуже приспособлены к передаче усилий (особенно сосредоточенных) с одного элемента на другой [1]. В связи с этим при проектировании трехслойных конструкций большое внимание уделяется рациональному выбору соединений с другими элементами.

В настоящее время имеется определенный опыт в решении задачи образования соединений трехслойных панелей с элементами конструкций [1, 2, 3]. Наиболее часто используются специальные вкладыши в виде распорных втулок, самоконтрящих гаек или одностороннего крепежа (рис.1). Перед постановкой вкладыша в верхнем слое обшивки сверлят отверстие, в которое заливают эпоксидный клей. Клеевая масса при уста новке вкладыша заполняет впадины, создавая достаточную прочность соединения.

Анализ существующих способов постановки резьбового вкладыша [3] показал, что они обладают малой производительностью. Кроме того, за счет клея увеличивается масса силовой точки.

Для устранения данного недостатка авторами разработана конструкция вкладыша [4] и способ его постановки (рис.2), который заключается в осевом пластическом сжатии материала вкладыша. В процессе осевого сжатия происходит радиальная раздача вкладыша по внешнему диаметру с образованием тороидальной поверхности. Сформированная тороидальная поверхность позволяет зафиксировать вкладыш между верхней и нижней обшивками.

При моделировании процесса постановки резьбового вкладыша и проектировании технологического оборудования необходимо знать величину работы и усилие, необходимые для осевого сжатия элемента. Кроме того, необходимо получить аналитические

Рис. 1. Варианты конструктивного выполнения вкладышей в трехслойных конструкциях

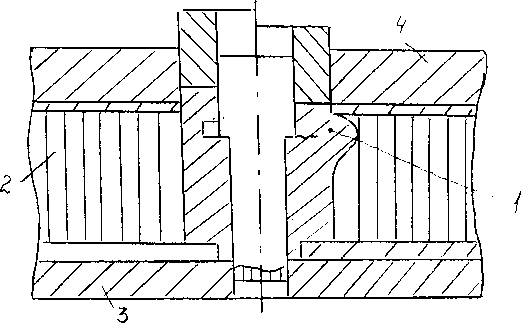
Рис. 2. Схема постановки в сквозное отверстие трехслойной конструкции: 1 - вкладыш;

2 - трехслойная конструкция; 3 - подштамповая плита; 4 - прижимная плита

^Лд = ^Лвн ^{+ Л}ТР.Т . ^{+ Л}ТР . в . ^{+ Л}СР .

Работу внутренних сил для материала вкладыша, подчиняющегося уравнению состояния пластической среды с нелинейным упрочнением, можно представить в виде

соотношения, определяющие деформированное состояние материала по внешнему контуру вкладыша в зависимости от его геометрических параметров.

Усилие, необходимое для осевого пластического сжатия резьбового вкладыша, можно определить с помощью энергетического метода [5], а работу внешних сил Л ₇ , нормальных к торцу втулки, можно записать в виде:

Л ₇ = JJ ( 7 _Z • и • dF = и • p , (1)

F где и - деформирующей ход; p - усилие осадки.

Из условия равенства работ внешних сил Л о ^ и сил деформирования вкладыша Л_д получим

^Л" = V5 О-(1 + n )^^Г''*"'• ⁽⁴⁾ где о _в - предел прочности материала вкладыша £ _t - относительное сужение, соответствующее образованию устойчивости шейки; n = £ _t /(1 - £ _t ) Г - интенсивность деформации сдвига. Для случая плоского напряженного состояния и равномерной раздачи вкладыша интенсивность деформации сдвига определяли из выражения [5]

Г= J £ e _z . (5)

Здесь £ _Z = (( h ₀ - h )/ h ₀ ) , где h₀ - первоначальная сумма зон А и В; h - высота зон А и В после деформации.

Подставив пределы интегрирования в (4) и учитывая (5), получим:

A вн

7 в

V3 ( 1 - £ _t ) ( ^£ _t )* ( 1 + n )

X JJJ ( ^^£ Z ) rdrd ^ dz =

V

X

Л д Р =---.

и

a_B • u¹⁺ⁿ ( R - r ) • r • n V3 ( i - £ t д ( i + n ) .

Определение Лд производилось исходя из граничных условий на внешнем контуре вкладыша. На верхнем торце вкладыша действует сила трения (рис.3). В процессе осадки вкладыша основная часть деформации приходится на зону А. В плоскостях контакта пластической зоны А и жестких зон В и С возникают силы среза.

Будем считать втулку пластическим телом с нелинейным упрочнением.

Полная работа сил деформирования складывается из работы внутренних сил Л_вн, идущих на изменение формы втулки, работы сил трения по торцу втулки Л_ТРТ и по внутренней поверхности Л_Трв, работы сил среза Л_СР между пластической и жесткой зонами

Работу сил трения на торце втулки оп-

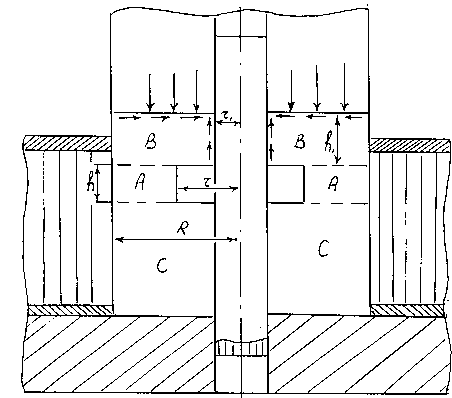
Рис. 3. Схема деформирования вкладыша ределяли с учетом принципа Сен-Венана, который позволяет принять систему приложенных сил, в частности сил трения, равномерно распределенными по поверхности тела. В связи с этим среднее значение сил трения можно определить из следующих выражений [6]

^T = V ⁽V ^{T 2 + T} p r ) = V ^{- Т}(О.      (7)

где T _rz и т ^, - касательные напряжения.

Здесь у - эмпирический коэффициент, учитывающий состояние трущихся поверхностей и форму очага деформации;

V = Ц ^{+ 1} ■    ( 1 - Ц)ft ;

8 ho где ц - коэффициент трения; b = R - r ; R -внешний радиус втулки; Т(Г) — интенсивность касательных напряжений,

Т ( Г ) = о в -Г ”/ Л ( 1 - е , )(Л е , ) n .

где u_Z = e_Zz ; r 1 - внутренний диаметр втулки.

Работу сил среза между пластической зоной А и жесткими зонами В и С можно определить из следующего выражения:

ACP

2 n h R

= 2 JJ T ( Г ) ( u R

0 r

- u_R B ) rdzd p =

O B • u n ^{+ 1} n ( R - r ) - r V3 (1 - e , > ," h n

где U RA и U_RB - перемещения в зонах А и В.

Учитывая (3), (6), (8), (9), (10), окончательно запишем

A д =

OR ■ un+1п B et(1 - et )hn

[ ^{( R -} r ^{) - x} _ ( 1 + h )

r v ■ R ■ r₁

+

V ■ r ₀ ■ h ( R - r ) ■ r

Таким образом, работу сил трения по верхнему торцу вкладыша можно представить следующим образом:

A

TP . T .

2 п R

= V JJ T ( Г ) urdrd p =

0 r ₁

VO B - u n ^{+ 1} R - r 1 - n 2 h n Ce ; ( 1 - e , ) .

Работа сил трения, совершаемая по внутреннему контуру втулки, определяется аналогично:

2 n h

A TP . B . = V J J T ( Г ) u Z rdzd p =

0 h

VO B • u n ^{+ 1} R - r 1 - n

Л (1 - e, Kir ^{- 1}

Из (11) с учетом (2) можно найти усилие, необходимое для осевого пластического сжатия резьбового вкладыша.

Процесс постановки резьбового вкладыша в отверстие трехслойной конструкции может быть осуществлен на установке с магнитно-импульсным приводом (рис.4), представляющей собой сложную электромеханическую систему, от выбора параметров которой существенно зависят масса и габаритные размеры инструмента, и обеспечивается необходимая скорость бойка при ударе.

В работе [7] разработана методика расчета магнитно-импульсного инструмента применительно к однослойным индукторам (рис.4). Проведенные исследования показали, что кинетическая энергия ударника должна быть больше величины А д на величину потерь, приходящихся на упругие деформации и перемещение элементов машин, силы трения.

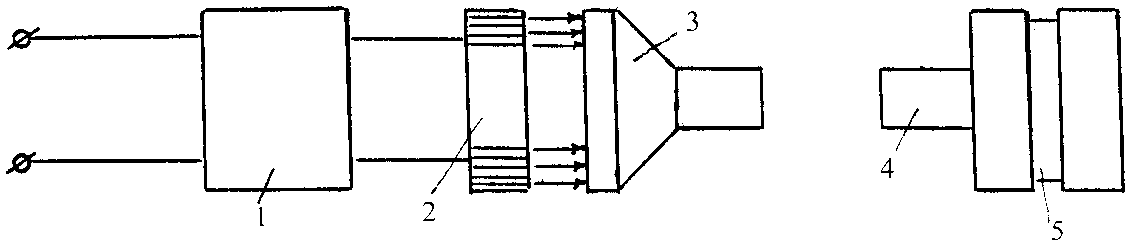
Рис. 4. Принципиальная схема установки с магнитно-импульсным приводом для динамической осадки подкрепляющей втулки: 1 - энергоблок; 2 - индуктор; 3 - ударник; 4 - пуансон; 5 - деталь

Кинетическую энергию установки можно определить из следующей зависимости:

mV 1 л -----= k ■ A_n

1 Д ’

где k=1,5...2 - эмпирический коэффициент, учитывающий потери; m - масса бойка; V -скорость бойка.

Исходя из рабочего напряжения накопителя энергии и₀ и кинетической энергии, вычисляли емкость накопителя C, частоту разрядного тока ш и число витков индуктора N

N ■ min

3I ( 23,8 R, ^1,25 ■ 7 0,5 ■ k 3 ■      ( 1 - k Г )

\         (1 + k F

V                                      /

Здесь L - индуктивность контура "индуктор-боек"; R 0 - активное сопротивление соединительного кабеля, наполнителя и коммутатора; k₃ - коэффициент заполнения обмот^ки; k з = fN/^ ^{- r} 2 ) ; f^- толщина шины, из которой сделана обмотка индуктора; где r 1 и r₂ - соответственно внешний и внутренний радиусы индуктора; k = r ₂ /r ; Y 1 и у ₂ - электропроводность материала соответственно обмотки и бойка.

С помощью разработанной методики окончательно выбирают такое количество витков и такой тип индуктора, при котором КПД максимален. В этом случае энергоемкость накопителя максимальна.

Для определения конструктивных параметров резьбового вкладыша в работе проведены экспериментальные исследования по влиянию конструктивно-технологических параметров процесса осевого пластического сжатия материала вкладыша на размеры и форму образуемой тороидальной поверхности.

Экспериментальные исследования проводили в соответствии с методом планирования экспериментов Бокса-Уилсона. В ка честве параметра оптимизации было выбрано отношение tW , где t - радиальная раздача; W - высота выступа. В качестве конструктивных параметров исследовались глубина и высота проточки, толщина стенки вкладыша, а также его внутренний и внешний диаметры. Исследования проводили в статическом и динамическом режимах осадки резьбового вкладыша. Для определения размеров и формы раздачи вкладыша по внешнему диаметру изготавливали шлифы. Замеры проводили на инструментальном микроскопе УИМ-21 с точностью до 0,001 мм. На основе результатов экспериментов были найдены коэффициенты модели и получено уравнение регрессии.

Зависимость деформаций по внешнему контуру резьбового вкладыша от геометрических параметров при его постановке находили с помощью принципа минимума полной энергии деформации и метода Ритца. Радиальное перемещение представлялось в виде

1     1 У ur = -ar 1--- r 2 h2

Выражение (14) выбирали с учетом формы радиальной раздачи вкладыша, полученной при экспериментальных исследованиях процесса его осадки.

Для нахождения параметра а составляли вариационное уравнение. С учетом граничных условий (рис.3) оно имело следующий вид:

^Д = ^ ^АВЯ ⁺ ^ ^ACP ⁺ S A TP.B. , ⁽¹⁵⁾ где 3 A_BH , 3 A_CP , 3 A_{TP B} - вариации работ соответственно внутренних сил, идущих на изменение формы вкладыша, сил среза между пластической и жесткой зонами и сил трения по внутренней поверхности вкладыша.

Подставив в (15) найденные вариации работ и выполняя варьирование по а с учетом (14), получим:

^

V3 ( 1 - £ t ⁾⁽ V3 £ t ) ( 1 + n )

х

X

2 n R h

JJJ

dr ^{1 +} n d a

rdrd ф dz +

+

2j J ^

0 r

d a

+

2 n h JJ 00

d ^ ⁽ u z ^)] d a

- r1

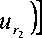
rdrd ^ +

rd ^ dz = 0.

Произведя необходимые вычисления и используя метод приближенного дифференцирования, получим

- n + 1

^ Z

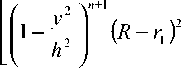
(А-А ^ зЛ • h

+ у • h • r

J

Таким образом, зная a, а также геометрические параметры вкладыша, из (14) можно найти и.

Из (17) с учетом экспериментальных данных через осевую деформацию £ _ можно найти деформирующий ход A h вкладыша.

Таким образом, используя предложенные в работе аналитические зависимости и данные, полученные экспериментальным путем, можно оценить степень деформированного состояния резьбового вкладыша и энергосиловые параметры при его постанов

ке в отверстие трехслойной конструкции.