Моделирование температурных полей в слоистых телах при малых значениях времени

Классические решения задач теплопроводности получаются, как правило, в виде суммы плохосходящихся рядов по собственным функциям задачи. Они очень неудобны для практического применения при малых значениях времени из-за медленной сходимости рядов, представляющих решение. Это неудобство особенно сильно проявляется при определении максимальных значений температуры, которые реализуются на коротком временном интервале при импульсном воздействии теплового потока на поверхности. Целью является определение приближенного поля темпера -тур при небольших значениях времени и удобным для практического применения. Для этого, после перехода в плоскость изображений по Лапласу, изображения разлагаются в быстросходящийся ряд, и далее в разложении удерживают первый член. Переходя далее в плоскость оригинала, получают поле температур при небольших значениях времени. Для случая однослойного цилиндра удалось получить простые аналитические выражения. В общем случае, применяется численное обращение полученных изображений. Для этого используется эффективная модификация численного метода отыскания оригинала, предложенного А.Популисом. Модификация позволяет повысить точность вычислений, а также улучшить сходимость полученного ряда. Для определения поля температур при небольших значениях времени, получается ряд, состоящий из семи членов.

Подобные задачи были рассмотрены в работах [1, 2, 3]. В работах [1, 2] для определения нестационарного трехмерного температурного поля в к-слойном цилиндре. используется следующий подход: сначала с помощью метода конечных интегральных преобразований исключаются дифференциальные операции по продольной координате, а затем полученное уравнение в изображениях решается методом Фурье (разделения переменных), что позволяет свести определение временной зависимости темпера -туры к решению обыкновенного дифференциального уравнения первого порядка.

В работе [3] для определения температурного поля в изделии цилиндрической формы при несимметричном конвективно-радиационном теплообмене поверхностей. на основе стандартной функции pdepe в среде matlab была разработана программа, позволяющая по заданным теплофизическим характеристикам материала и параметрам конвективнорадиационного теплообмена моделировать температурное поле в изделии.

В работе [4] описываются температурные поля при оплавлении заусениц в камерах для термодинамической обработки материалов, возникающих при термоимпульсной детонации горючими смесями.

Температурные поля на полусферических поверхностях контактных устройств были рассчитаны численным методом в работе [5].

В работе [6] были получены температурные поля в двухслойной пластине, подверженной воздействию теплового потока на одной из поверхностей.

В работе [7] получены асимптотические выражения для периодических температурных полей на больших значениях времени.

Вывод основных уравнений

Поля температур в стенках двухслойных цилиндрических сосудов оп ределяются системой уравнений теплопроводности:

(В дальнейшем для простоты полые двухслойные цилиндрические со суды будем обозначать камерой).

1 дt   д2 t   1 дt i = 1,2

--L =---2. +--L ai дт   дr2   r дr при начальных условиях:

t , ( r ,0) = 0, i = 1,2

и условиях на поверхностях:

Z1 ^t1^ = -Q(т), t2(R ,т) = 0, д r дt.(R -0,т)      дt2(R + 0,т)          A 4              A

• X 1 ^1V * ’ = X 2       ’        , t ( R - 0, т ) = 1 2 ( R + 0, т ).

• д r               д r

Здесь r ₀, R 2 — внутренний и внешний радиусы камеры, R 1 — радиус границы сопряжения слоев, где соблюдаются условия идеального теплового контакта (3).

Q ( т ) = Q 1 (1 - 0 ) e "  + Q 2 e " ^k 2 ^т (4) — заданный тепловой поток на внутренней поверхности. Q 1 , Q ₂, к 1 , к ₂ — постоянные, зависящие от геометрических размеров камеры, состава газовой смеси, а также от величины начального давления. Первое слагаемое, которое вносит основной вклад в величину теплового потока (около 90%), описывает передачу тепла к стенкам камеры за счет конвекции и естественного излучения, второе слагаемое характеризует перенос тепла за счет вынужденных конвективных потоков, порожденных ударными волнами.

Внешняя поверхность поддерживается при постоянной температуре. X,, ai, i = 1,2 — коэффициенты теплопроводности и температуропровод- ности первого и второго слоев.

Общее решение систем уравнений теплопроводности в плоскости изображений по Лапласу выглядит следующим образом:

t"(г,p) = C, 110(q,r) + C,2K0(q,r), i =1,2 , где p — переменная Лапласа, qi =

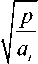
, I ₀ , K ₀ — модифицированные

функции Бесселя. Постоянные С, 1, С,2 определяются из граничных усло- вий (3) и условий сопряжения слоев после применения к ним преобразования Лапласа.

Асимптотические разложения модифицированных функций Бесселя при больших значениях аргументов qt, г, которым в плоскости оригина лов соответствуют малые значения времени, имеют вид:

I n ⁽ qr ) =-/ =

K ( qr ) =J    e

N ² qr

1 4 n ²

— 1   (4 n ² — 1)(4 n ² — 3²)

1!8 q , r

2! ( 8 qr ) ²

4 n ² — 1   (4 n ² — 1)(4 n ² — 3²)

1!8 q , r

2! ( 8 qr ) ²

...

,

.

В этих разложениях, ограничиваясь только первым членом и принимая, что e—2( q1 h1 + q 2 h 2)

,² q 2 h :

получим после некоторых выкладок для изображений поля температур , в первом слое:

t i ^{( г} , Р ) =

X + e

X + — X — e q^1h1

— e

где:

X + = ^X + ' , X — Ф 1 Ф 2

= X

Xг

Ф 1

Ф 2

во втором слое:

t 2 ⁽ r , Р ) =

- e ~ ^q 1 h 1

e

q ₂ ⁽ г ^- RV)

—

e

q 2 ⁽² R 2 - R i - r )

X + — X — e "² qh¹

Здесь ф ² = a_t , г = 1,2; Q ( p ) — изображение теплового потока в кости Лапласа и имеет вид:

плос-

kh-

Q ( Р ) = Q 1 (1 — 9 ) - — 7 Л -1^ e^{4 p} Р ² P V P

+ ^Q 2

p + к ₂

.

Соответствующие оригиналы для изображений (5) и (6) представляют собой приближенные температурные поля в двухслойной камере при небольших значениях времени. Ввиду громоздкости изображений обращение осуществляется численно. Наилучшие результаты получаются при семи членах в формуле обращения. В этом случае алгоритм обращения имеет вид:

f ( х ) = ⁶⁴^¹ⁿ² ( — 0,25 F (3 о ) + 10 F (5 о ) — 106 F (7 о ) +

где о =--- x

п х

+ 448 F (9 о ) — 864 F (11 о ) + 768 F (13 о ) — 256 F (15 о )), 1n V2

.

Для случая однослойной камеры ( а₁ = а ₂, х ₁ = х ₂ ) изображения поля температур принимают более простой вид:

7 ( r,p ) = Qp E{ e —

X 1 4 1 V r

q ( r ^— r o ) ₊ e

— I

4 1 ⁽² kr o ^— r o ^— r ) }

R

•

Здесь обозначено к = — r o

Для изображений температуры внутренней поверхности (r = r0) по- лучим:

t ^{( r} , Р ) =

Q ( Р )

X i 4 i

Для этого выражения удалось получить оригинал, который имеет вид:

t ( Г о , т ) = ^-{Q i (i — 0 ) X i

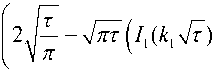
^— L ( k 1 ^ ) )

2 е^{— к}т г 2

+ Q ₂ -= e    J eu du }.

V n ki^ o

Здесь 1 ₁ — модифицированная функция Бесселя первого рода, L₁ — модифицированная функция Струве.

Область применения полученных приближенных решений во времен-

ном интервале оценивается путем сравнения с результатами точного ре-

шения задачи.

Так, для оценки применимости формулы (Ю) были получены выражения для температуры в однослойном цилиндре при тех же начальных и

граничных условиях:

t ⁽ Г ^{, т} ) = ^— r o

to

• ln r • Q ( т ) + п ^

к = 1

^{1 1} 1 ⁽ Y k^r o ^{) — 1}o ⁽ Y k R 2 ) Y k I ?^г>) — IKxR 2 )

• [ — Y o ( y_k R 2 ) • I o^ Y k r o^ + 1 1 ( / k R 2 ) • Y o ( r k r o ) ] ^ Ф к ( т )

где

Здесь

Ф k ( т ) = — ( Q 1 + Q ₂ (1 — 0 ) ) e ^{— y 2 t} + Q 1 Z 1 + Q 2 (1 — 0 ) z 2 .

1 — Y_tT z ₁ = —e ^{Y k}

Y k

r A

• I -b_ | + e 12Y J

— I

t I     Г k

• I Yk^т — /

I          ² Yk,

;

^z 2 =

V k ^{— k} 2

⁽ e ^— '

— e

yXt

);

x

I ( х ) = e • J e dz

— интеграл Доусона.

o

Собственные числа yk определяются из характеристического уравне ния:

I^р ;, ) - 'My R ) - Y ^) - 1 o Y R ) = 0 .                  (12)

Чтобы облегчить вычисления, с помощью замены переменных:

х = П (r - R 2), и (х) = V(*) , H = R 2 - Го HH х + Го

V п исходная задача о собственных функциях сводится к типичной задаче Штурма — Лиувилля [4]. Затем для определения асимптотических значений корней исходного характеристического уравнения (12) получим следующее трансцендентное уравнение:

8/rn

.

tgY =--0—

H (4 - H )

Решение этого уравнения позволяет указать интервал, в котором заключен корень уравнения (12), кроме первого значения, что значительно упрощает вычисления.

Область применения полученных приближенных решений оценивается путем сравнивания с результатами точного решения задачи. Результаты расчета по формуле (10) сравнивались с точными решениями, полученными по формуле (11) для однослойного цилиндра. Сопоставление результатов расчета показало, что областью применимости приближенной формулы (10) при принятых расчетных данных можно считать интервал (0-32 сек). При т ₀ = 20 сек относительная погрешность составила ~ 1%.

Для оценки погрешностей при вычислении полей температур для двухслойной камеры с помощью процедуры численного обращения (8), сопоставление с точным решением задачи производится для значений температуры внутренней поверхности двухслойного цилиндра.

На рис. 1 изображены графики изменения температуры внутренней поверхности однослойного и двухслойного цилиндра на промежутке времени, составляющим один цикл воздействия теплового потока (4).

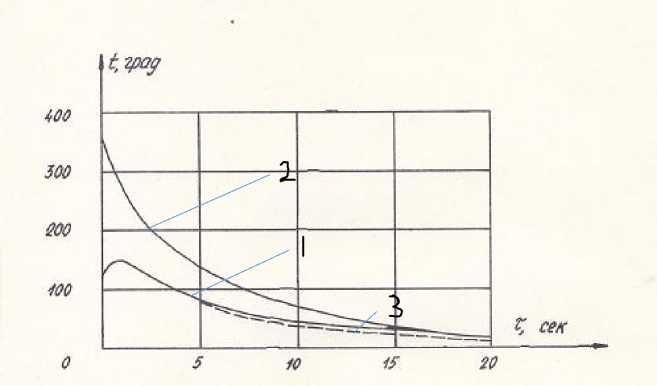
Рис. 1. Изменение температуры внутренней поверхности однослойного и двухслойного цилиндра

Было принято T = 20 сек. Точные решения изображены здесь сплошной линией. Кривая 1 соответствует двухслойному цилиндру, кривая 2однослойной. Приближенное решение для температуры внутренней поверхности двухслойного цилиндра описывается штриховой линией (кривая 3). Приближенное и точное значение температуры внутренней поверхности однослойного цилиндра совпадают с высокой степенью точности (оба решения изображены одной сплошной линией 1). Из рисунка видно, что для двухслойного цилиндра приближенное решение имеет удовлетворительное соответствие с точным решением лишь вплоть до значений 10 сек. При т ₀ = 20 сек относительная погрешность составляет ~ 5%. По-видимому, областью применимости приближенных формул для определения поля температур с использованием процедур численного обращения (8) следует считать т ₀ = 9 ^ 10 сек. Более худшие результаты по сравнению с аналитической формулой обращения (8) связаны, по-видимому, с погрешностью численного обращения.

Константы материалов внутреннего и внешнего слоев, принятые при расчете, соответствовали характеристикам меди и стали:

Р1 = 8,93-гу, р2 = 7,17г, С, = 0,0926кал, см           см             г • град кал               кал                  кал

С2 = 0,105-------, Х1 = 0,96--------------, х2 = 0,13--------------, г • град           см • сек • град           см • сек • град h1 = 0,4см, H = 4см, r0 = 28см, R2 = 32см.

Заключение

Таким образом, предложена формула для определения температурного поля в стенках однослойного и двухслойного цилиндров при сравнительно небольших значениях времени. Процедура, заключающаяся в суммировании ряда из семи членов, представляет собой весьма удобный метод расчета для нахождения температуры внутреннего слоя для двухслойного цилиндра при небольших значениях времени, где имеет место наибольшее значение поля температуры. Для определения температуры внутренней поверхности однослойного цилиндра получена аналитическая формула, имеющая высокую степень точности на всем промежутке времени, составляющем один цикл воздействия тепловым потоком.